Kernel Methods

김민재·2024년 6월 13일
ML
0

ML

목록 보기
17/17

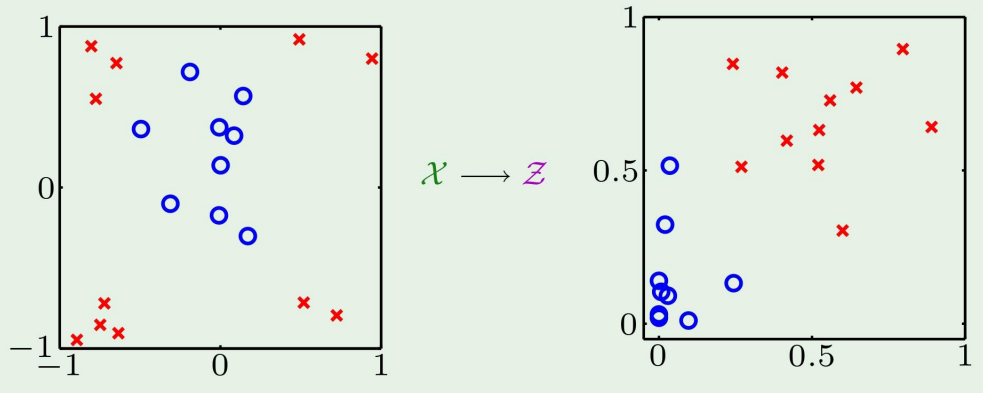
저번에 우리가 X\mathcal{X} space에서 Z\mathcal{Z} space로 공간을 이동시켰고, 이렇게 하는 방법이 kernel method라고 하였다.

이 방법을 자세히 다뤄보자.

SVM에서의 L(α)\mathcal{L}(\alpha) 식을 다시 떠올려보자

L(α)=∑n=1Nαn−12∑n=1N∑m=1NynymαnαmxnTxm\mathcal{L}(\alpha) = \sum_{n=1}^N\alpha_n - \frac{1}{2}\sum_{n=1}^N\sum_{m=1}^N y_ny_m\alpha_n\alpha_m\mathbf{x}_n^T\mathbf{x}_m

이 식은 현재의 space가 X\mathcal{X}인 경우이다. 그렇다면 우리의 공간이 Z\mathcal{Z}로 바뀌고 난 후의 식은,

L(α)=∑n=1Nαn−12∑n=1N∑m=1NynymαnαmznTzm\mathcal{L}(\alpha) = \sum_{n=1}^N\alpha_n - \frac{1}{2}\sum_{n=1}^N\sum_{m=1}^N y_ny_m\alpha_n\alpha_m{\color{Purple} \mathbf{z}_n^T\mathbf{z}_m}

가 될것이다.

그리고 우리가 찾은 best hypothesis를 g(x)g(x)라고 하자.

그리고 여전히 bipolar 문제에 대해서만 예시를 들어보면,

g(x)=sign(wz+b)g(\mathbf{x}) = \text{sign}(\mathbf{w}{\color{Purple}\mathbf{z}} + b)

라고 했을때, 우리가 SVM에서 얻었던 w\mathbf{w}와 bb의 식에서 xx만 zz로 바꿔주면 된다.

w=∑zn is SVαnynzn\mathbf{w} =\sum_{{\color{Purple} \mathbf{z}_n}\text{ is SV}}\alpha_ny_n{\color{Purple} \mathbf{z}_n}
b:ym(wTzm+b)=1b : y_m(\mathbf{w}^T{\color{Purple} \mathbf{z}_m}+b)=1

그렇다면 이 식들에서 얻을수 잇는 결론은 우리가 원하는 solution을 찾으려면, znTzm{\color{Purple} \mathbf{z}_n^T\mathbf{z}_m}를 찾아야 한다.

이제 또 지금껏 그랬듯이, x\mathbf{x}의 inner product와 z\mathbf{z}의 inner product가 어떤 함수로 표현될수있다면? 하는 생각을 해보자.

Let   zTz′=K(x,x′)\text{Let }\;{\color{Purple} \mathbf{z}^T\mathbf{z}'} = K(\mathbf{x,x'})

그리고 우리가 원하는것은 결국 inner product이므로, 하나의 scalar 값으로 나오게 된다.

한가지 예시로, 기존의 x=(x1,x2),R2→2nd-order Φ(R6)\mathbf{x} = (x_1,x_2), \mathbb{R}^2 \to \text{2nd-order }\Phi (\mathbb{R}^6) 으로 바꿔보자.

그렇다면 z=Φ(x)=(1,x1,x2,x12,x22,x1x2){\color{Purple} \mathbf{z}} = \Phi(x) = (1,x_1,x_2,x_1^2,x_2^2,x_1x_2)이라고 한다면,

K(x,x′)=zTz′=1+x1x1′+x2x2′+x12x1′2+x22x2′2+x1x1′x2x2′K(\mathbf{x,x'}) = {\color{Purple} \mathbf{z^Tz'}} = 1 + x_1x_1' + x_2x_2' + x_1^2x_1'^2 + x_2^2x_2'^2 + x_1x_1'x_2x_2'

가 된다. (두 점의 inner product이므로)

그렇다면 우리가 과연 K(x,x′)K(\mathbf{x,x'})를 x,x′\mathbf{x,x'}을 변환하지 않고 계산할수 있을까??

K(x,x′)=(1+xTx′)2=(1+x1x1′+x2x2′)2=1+x12x1′2+x22x2′2+2x1x1′+2x2x2′+2x1x1′x2x2′\begin{aligned} K(\mathbf{x,x'}) &= (1+\mathbf{x^Tx'})^2 = (1+x_1x_1'+x_2x_2')^2\\ &= 1 + x_1^2x_1'^2 + x_2^2x_2'^2 + 2x_1x_1'+2x_2x_2'+2x_1x_1'x_2x_2' \end{aligned}

kernel을 우리가 저렇게 놓으면, 전개한 식이 나오게 되는데, 이는 아래 ZZ의 inner product로 표현된다.

z=(1,x12,x22,2x1,2x2,2x1x2)z′=(1,x1′2,x2′2,2x1′,2x2′,2x1′x2′)\begin{aligned} \mathbf{z} &= \left( 1, x_1^2, x_2^2, \sqrt{2}x_1, \sqrt{2}x_2, \sqrt{2}x_1 x_2 \right) \\ \mathbf{z}' &= \left( 1, x_1'^2, x_2'^2, \sqrt{2}x_1', \sqrt{2}x_2', \sqrt{2}x_1' x_2' \right) \end{aligned}

The polynomial kernel

원래의 X=Rd\mathcal{X} = \mathbb{R}^{\color{Purple}d} 일때, Φ:X→Z\Phi : \mathcal{X}\to\mathcal{Z}는 legendre polynomial의 order Q{\color{Red}Q}로 표현이 가능하다.
위에서 보았던 kernel을 보면,

K(x,x′)=(1+xTx′)Q=(1+x1x1′+x2x2′+⋯+xdxd′)Q\begin{aligned} K(\mathbf{x,x'}) &= (1+\mathbf{x^Tx'})^{\color{Red} Q}\\ &= (1+x_1x_1'+x_2x_2' + \cdots+x_{\color{Purple} d}x'_{\color{Purple} d})^{\color{Red} Q} \end{aligned}

이 되게되고, 어차피 우리가 Regularization에서 보았듯이, 제약조건을 걸어주기때문에 QQ가 높아져도 상관없다.

그리고 위 식에 상수를 더해 다음처럼 쓸수있다.

K(x,x′)=(axTx′+b)QK(\mathbf{x,x'}) = (a\mathbf{x^Tx'}+b)^{\color{Red}Q}

Radial Basis function

위의 polynomial kernel말고도, 아래의 kernel이 존재한다.

K(x,x′)=exp⁡(−γ∥x−x′∥2)K(\mathbf{x,x'}) = \exp \left ( -\gamma \left \|\mathbf{x - x'} \right \|^2 \right)

Kernel in action

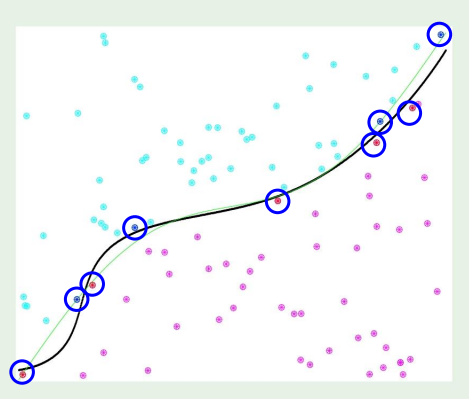
X\mathcal{X}에서 ,∞\infin-dimensional Z\mathcal{Z}로 변환했을때, 이때에도 Support vector의 갯수는 변하지 않는다.

Kernel formulation of SVM

원래 original space에서 solution을 찾기위해 quadratic programming으로 문제를 풀었다. (SVM-3)

여기서도 바뀌는것은 단지 x\mathbf{x}에서 kernel로만 변경해주면 된다!

따라서 우리의 최종 hypothesis는

g(x)=sign(∑αn>0αnynK(xn,x)+b)g(\mathbf{x}) = \text{sign} \left ( \sum_{\alpha_n>0} \alpha_ny_n {\color{Blue} K(\mathbf{x}_n,\mathbf{x})} +b\right )

가 되게 된다.

그런데 왜 kernel만 쓰면 모든 space가 정의될까? (Z\mathcal{Z} 가 존재한다는것을 어떻게 알까?)

→\to Mercer's condition

[K(x1,x1)K(x1,x2)⋯K(x1,xN)K(x2,x1)K(x2,x2)⋯K(x2,xN)⋮⋮⋱⋮K(xN,x1)K(xN,x2)⋯K(xN,xN)]\begin{bmatrix} K(\mathbf{x_1,x_1}) & K(\mathbf{x_1,x_2}) & \cdots & K(\mathbf{x_1,x_N})\\ K(\mathbf{x_2,x_1}) & K(\mathbf{x_2,x_2}) & \cdots & K(\mathbf{x_2,x_N})\\ \vdots & \vdots & \ddots & \vdots \\ K(\mathbf{x_N,x_1}) & K(\mathbf{x_N,x_2}) & \cdots & K(\mathbf{x_N,x_N}) \end{bmatrix}

이 행렬은 symmetric하다.
그렇다면, Mercer's condition에 따라 항상 positive semi-definite하다.

positive semi-definite하다는 것은 H≥0H\ge 0이라는 뜻이다.

함수의 값은 변하지 않거나 커진다.

profile
김민재
이전 포스트

Support Vector Machine-3

0개의 댓글