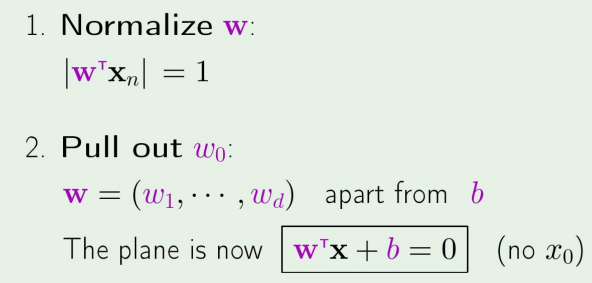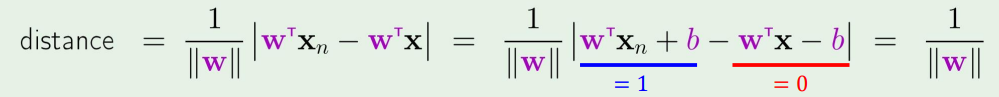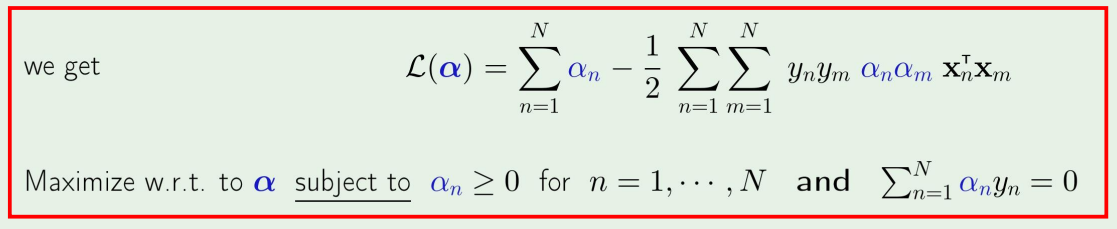이제 최종적으로 다시 원래 교재로 돌아와, SVM을 마무리 하겠다.
Better linear separation
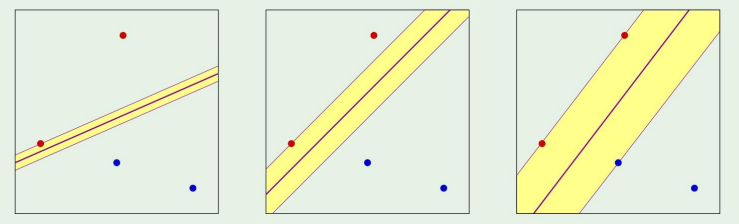
기존에는 그냥 단순히 저 보라색 선만 긋는, 즉 margin없이 분류하는것에 대해서만 배웠다.
그렇다면 margin이 왜필요할까?
결론부터 말하자면, margin이 Eout을 더 줄이기 때문이다.
margin을 가진 classifier는 VC dimension을 증가시키기도 한다.
예전에 dichotomies들을 떠올려보자.
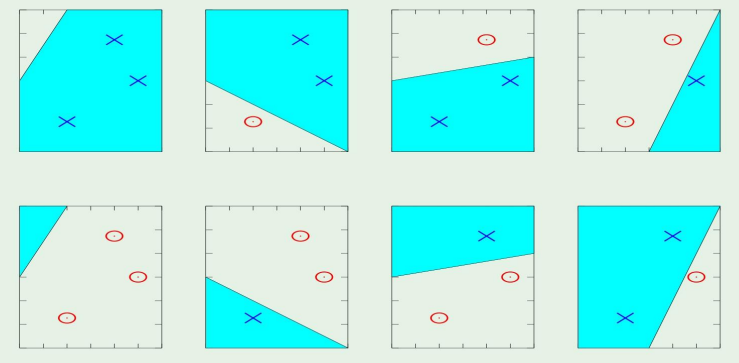
growth function을 사용해서 분류했던 기억이 날 것이다.
그렇다면 여기에 이제 margin을 적용해보면,
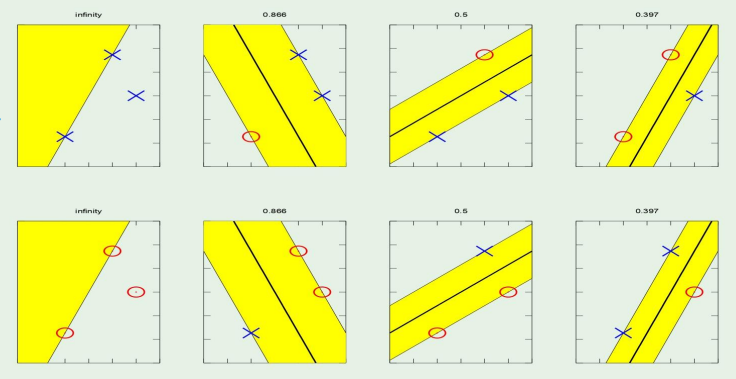
당연하게도 margin이 두꺼워질수록, 즉 fat 해질수록 더 적은 수의 dichotomies를 갖게 된다.
- Fat margin implies fewer dichotomies
- Fat dichotomies have smaller VC dimension as well as smaller growth function
- Indeed, the bigger margin allows the better out of sample performance
→ Fat margins are GOOD!
이제 아까 위의 그림에서 분류하는 보라색 선을 w라고 할때, 다음처럼 식을 놓자
wTx=0
그리고 xn을 위 식을 만족하는 x중에 가장 가까운 점이라 하자.
그뒤에,
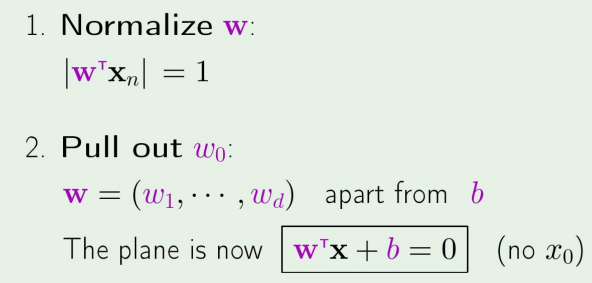
이렇게 만들자.
여기서 잠깐 거리 계산하는 식을 보자면,
xn과 우리가 정의한 plane wTx+b=0과의 거리는
X가 아래의 그림과 같을때,
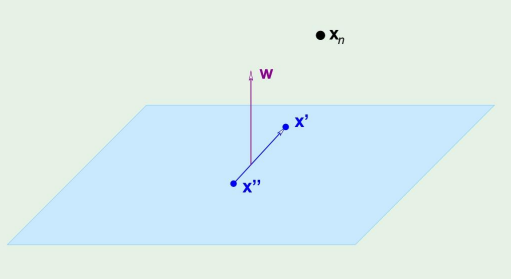
wTx′+b=0andwTx′′+b=0⇒wT(x′−x′′)=0
가 된다.
그렇다면 xn과의 거리는,
wnom=∥w∥w⇒distance =∣∣∣wnomT(xn−x)∣∣∣
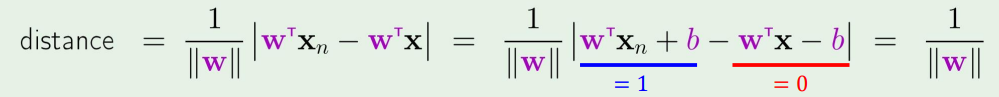
이렇게 계산된다.
∣∣w∣∣1 는 margin의 절반크기이다.
이제 optimization 문제로 돌아오면,
Maximize ∥w∥1
subject to n=1,2,⋯,Nmin∣∣∣wTxn+b∣∣∣=1
이고, 위 식을
∣∣∣wTxn+b∣∣∣=yn(wTxn+b)
로 만들면서, yn은 -1 or 1인 label이 된다.
근데 이제 w가 0이 되는 점에는 발산한다는 단점이 있기때문에, maximize하는것이 아니라, minimize 형태로 식을 바꾸고 정리하면,
21wTw
subject to yn(wTxn+b)=1for n=1,2,⋯,N
인 결론이 도출된다.
이제 한번더 solution을 볼텐데, 이번 글에서는 SVM은 regularization 문제와 같이 해결된다는 것을 보이기 위해,
아래의 글을 먼저 읽고 오자.
Regularization
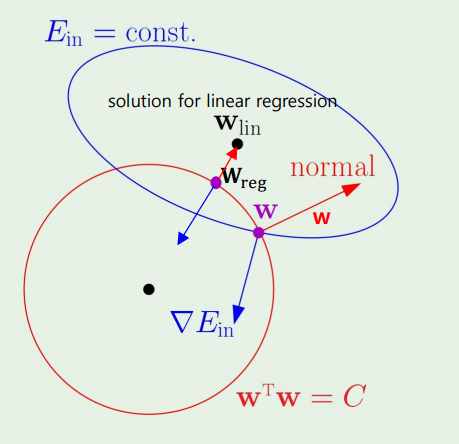
Regularization에서 이 그림을 보았다.
이 그림을 왜 다시 가져왔냐면, 결국 Regularization과 SVM은 똑같다는 것이다. 서로 Primal, Dual problem만 바뀐것 뿐이지 서로 같다.

다시 Lagrange formulation으로 돌아와 보면,
L(w,b,α)=21wTw−n=1∑Nαn(yn(wTxn+b)−1)
이 식에서 w와 b를 maximize 해야하고, gradient를 구하면
∇wL=w−n=1∑Nαnynxn=0
이 되고, 정리하면
∂b∂L=−n=1∑Nαnyn=0
이다.
그리고 이제 이 식을 Augmented target function에 넣고 정리하면 아래의 식이 나오게 된다.
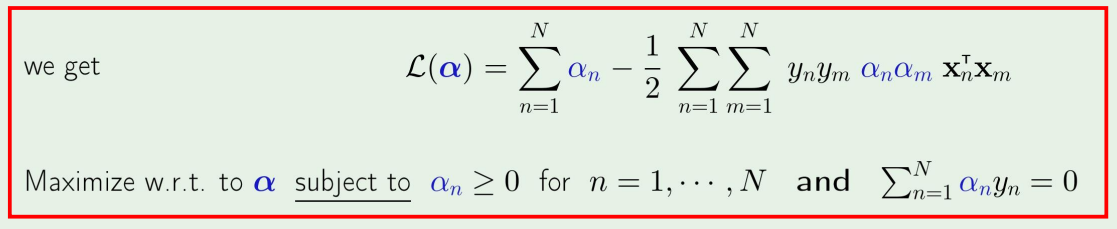
제곱꼴이므로 solution은 quadratic programming으로 풀면된다. →α 를 구할수있음

α를 구하면, 우리는
w=n=1∑Nαnynxn
을 구할수있고, KKT condition에 따라서,
αn(yn(wTxn+b)−1)=0
을 알수있다.
이게 무슨 뜻이냐면, αn(yn(wTxn+b)−1)=0 이라는 뜻은 α=0 이거나, 아니면 wTxn+b 가 1이라는 뜻이다.
근데 wTxn+b=1 인 경우는 slack condition으로 우리가 svm의 margin위의 점들이고, 따라서 이때의 α>0 이다.
반대로, wTxn+b=1 이라면, α=0 이다.
αn>0⇒xn is a support vector
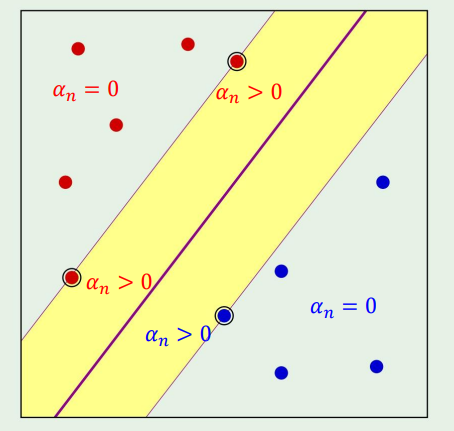
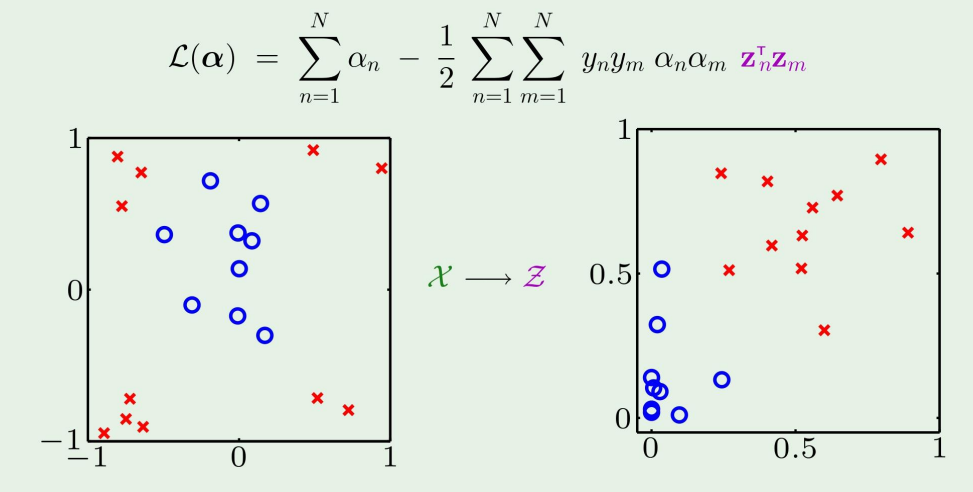
위 식을 풀면 margin의 결정경계를 얻을수있다.
그런데, x 대신에 z를 사용해도 원래 공간에서의 margin을 얻을수 있다는 것이다.
how? → Kernel method... in next post