Regularization

김민재·2024년 6월 12일
ML
0

ML

목록 보기
15/17

이번 장에서는 Regularization, 그중에서도 curve fitting problem만 간단하게 다뤄보겠다.

이러한 점들이 존재할때, 과연 몇차원으로 fitting을 해야할지 결정하는 것이다. (polynomial regression)

결론부터 말하면, 내 hypothesis space가 Legendre polynomials로 이루어 진다고 볼 수 있다.

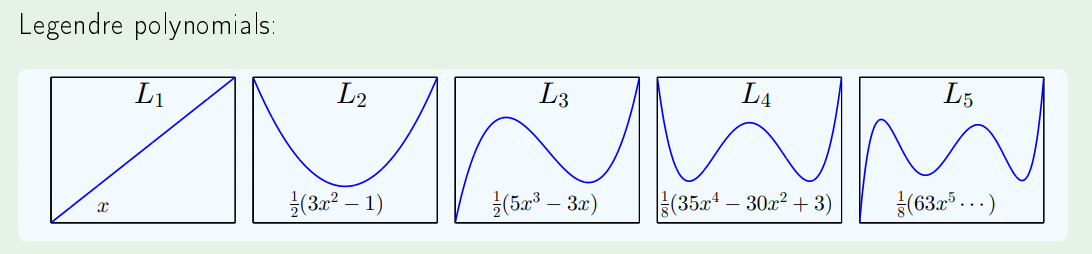
바꿔 말하면, 내가 구하려는 hypothesis, target function을 Legendre polynomials의 sum으로 볼수있다.

HQ:polynomials of order Qlinear regression in Z spacez=[1L1(x)⋮LQ(x)]H={∑q=0QwqLq(x)}\begin{aligned} &\mathcal{H}_Q :\text{polynomials of order }Q \qquad &\text{linear regression in }\mathcal{Z}\text{ space}\\ &\mathbf{z} = \begin{bmatrix} 1\\ L_1(x) \\ \vdots\\L_Q(x) \end{bmatrix} \qquad &\mathcal{H} = \left \{ \sum_{q=0}^Q {\color{Purple} w_q}L_q(x)\right \} \end{aligned}

그러면 우리가 (x1,y1),⋯ ,(xN,yN)(x_1,y_1),\cdots,(x_N,y_N) 이라는 점들이 주어졌을때, xx를 zz로 transform해 (z1,y1)⋯ ,(zN,yN)(\mathbf{z}_1,y_1)\cdots,(\mathbf{z}_N,y_N)로 나타내고,
이것을 이제 최소화 하는 w{\color{Purple}\mathbf{w}}를 찾아야 하므로,

Minimize   Ein(w)=1N∑n=1N(wTzn−yn)2Minimize   1N(Zw−y)T(Zw−y)wlin=(ZTZ)−1ZTy\begin{aligned} &\text{Minimize }\; E_{\text{in}}({\color{Purple} \mathbf{w}}) = \frac{1}{N}\sum_{n=1}^N({\color{Purple} \mathbf{w}^T}\mathbf{z}_n - y_n)^2\\ &\text{Minimize }\; \frac{1}{N}(\mathbf{Z}{\color{Purple} \mathbf{w}}-\mathbf{y})^T(\mathbf{Z}{\color{Purple} \mathbf{w}}-\mathbf{y})\\ &{\color{Blue} \mathbf{w}_\text{lin}} = (\mathbf{Z}^T\mathbf{Z})^{-1}\mathbf{Z}^T\mathbf{y} \end{aligned}

예전에 배웠듯이 normal equation으로 풀수있다.

이제 내가 어떤 curve fitting을 해야 하는데, 10개의 sum으로 나타내야될거 같다고 생각하자 →H10\to \mathcal{H}_{10}

그런데 여기에 제약조건이 걸리게 된다.

Hard constraint :  H2 is constrained version of H10 with wq=0 for q>2\text{Hard constraint }: \;\mathcal{H}_2\text{ is constrained version of }\mathcal{H}_{10} \quad \text{ with }{\color{Purple}w_q} = 0 \text{ for }q > 2

즉 L1,L2L_1, L_2를 제외하고는 모두 0으로 만들어 버린다는 뜻이다.

그러나 이렇게 하면 내가 원하는 fitting이 안될수도 있으므로, soft한 constraint를 부여한다.

Softer version :∑q=0Qwq2≤C   "soft-order" constraint\text{Softer version }: \qquad \sum_{q=0}^Q {\color{Purple} w_q^2}\le C \;\text{ "soft-order" constraint}

즉 L1,L2L_1,L_2까지는 원래의 식을 그대로 쓰고, L3L_3부터는 CC보다 작은 값으로 맞춰준다는 것이다.

이렇게 구속조건을 걸어준 뒤에, 다시 minimize를 하면,

1N(Zw−y)T(Zw−y)\frac{1}{N}(\mathbf{Z}{\color{Purple} \mathbf{w}}-\mathbf{y})^T(\mathbf{Z}{\color{Purple} \mathbf{w}}-\mathbf{y})
subject to:wTw≤C\text{subject to}:{\color{Purple} \mathbf{w}^T\mathbf{w}}\le C

아까와 같은 식에, wTw≤C{\color{Purple} \mathbf{w}^T\mathbf{w}}\le C 구속조건만 더해졌다.

이렇게 나온 w\mathbf{w}를, wlin{\color{Blue} \mathbf{w}_\text{lin}} 대신에 wreg{\color{Blue} \mathbf{w}_\text{reg}} 라고 하자.

Solving for wreg{\color{Blue} \mathbf{w}_\text{reg}}

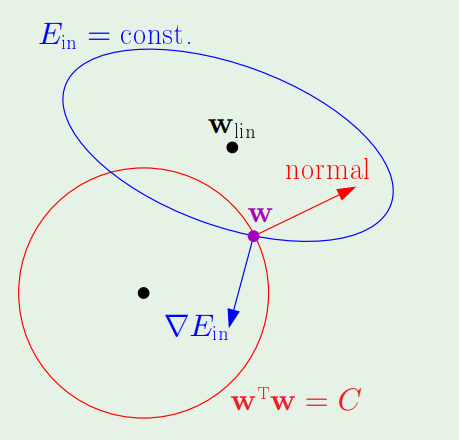
파란색원이 구속조건이 없는 상태이고, 그 위에 빨간색 원이 구속조건이다.

그렇다면 이제 식을 보자

∇Ein(wreg)∝−wreg=−2λNwreg\nabla E_{\text{in}}({\color{Blue} \mathbf{w}_\text{reg}})\propto - {\color{Blue} \mathbf{w}_\text{reg}}\\ = -2 \frac{\lambda}{N}{\color{Blue} \mathbf{w}_\text{reg}}
∇Ein(wreg)+2λNwreg=0\nabla E_{\text{in}}({\color{Blue} \mathbf{w}_\text{reg}}) + 2 \frac{\lambda}{N}{\color{Blue} \mathbf{w}_\text{reg}}=0
Minimize Ein(w)+λNwTw\text{Minimize }\quad E_\text{in}({\color{Purple} \mathbf{w}}) + \frac{\lambda}{N}{\color{Purple} \mathbf{w}^T}{\color{Purple} \mathbf{w}}

여기서 λ\lambda는 우리가 SVM에 Augmented target function의 그 λ\lambda 이다.

Solution

Minimize Eaug(w)=Ein(w)+λNwTw=1N((Zw−y)T(Zw−y)+λwTw)\begin{aligned} \text{Minimize }\qquad E_{\text{aug}}(\mathbf{\color{purple}{w}}) &= E_{\text{in}}(\mathbf{\color{purple}{w}}) + \frac{\lambda}{N} \mathbf{\color{purple}{w}}^T \mathbf{\color{purple}{w}} \\ &= \frac{1}{N} \left ((\mathbf{Z\color{purple}{w}} - \mathbf{y})^T (\mathbf{Z\color{purple}{w}} - \mathbf{y}) + \lambda \mathbf{\color{purple}{w}}^T \mathbf{\color{purple}{w}} \right) \end{aligned}
∇Eaug(w)=0  ⟹  ZT(Zw−y)+λw=0\begin{aligned} \nabla E_{\text{aug}}(\mathbf{\color{purple}{w}}) = 0 &\implies \mathbf{Z}^T (\mathbf{Z\color{purple}{w}} - \mathbf{y}) + \lambda \mathbf{\color{purple}{w}} = 0 \end{aligned}

이 식을 풀면 우리는 augmented target function에 대한 minimize를 할 수 있다.

wreg=(ZTZ+λI)−1ZTywlin=(ZTZ)−1ZTy\begin{aligned} {\color{Blue} \mathbf{w}_\text{reg}} &= (\mathbf{Z}^T\mathbf{Z} + \lambda\mathbf{I})^{-1}\mathbf{Z}^T\mathbf{y}\\ {\color{Blue} \mathbf{w}_\text{lin}} &= (\mathbf{Z}^T\mathbf{Z} )^{-1}\mathbf{Z}^T\mathbf{y} \end{aligned}

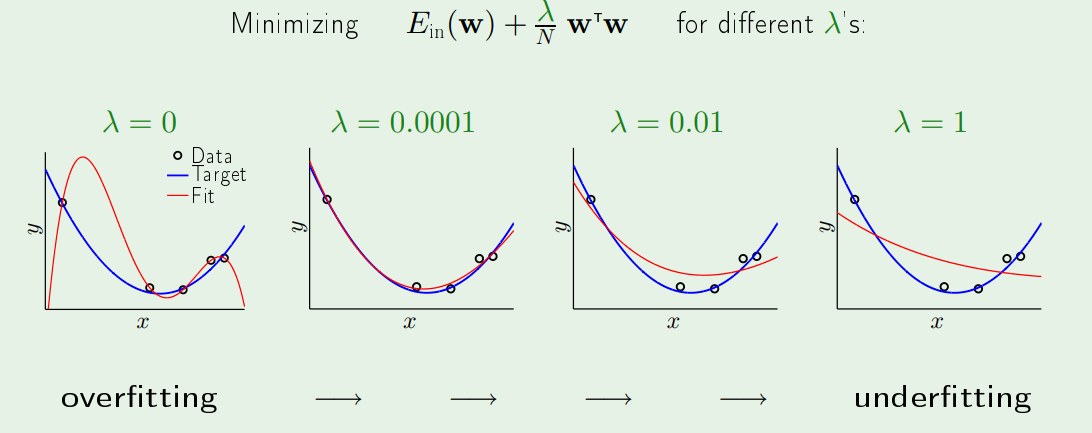
그림을 살펴보면 λ=0\lambda = 0일때는 no regulization을 한다는 의미이다.

그리고 그림의 식에 있는 wTw\mathbf{w}^T\mathbf{w}는 우리가 알고있는 Ridge Regularlization이다.

profile
김민재
이전 포스트

Support Vector Machine-2

다음 포스트

Support Vector Machine-3

0개의 댓글