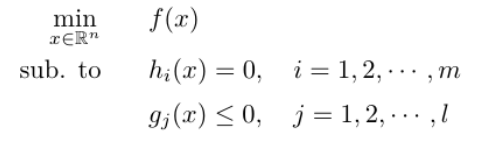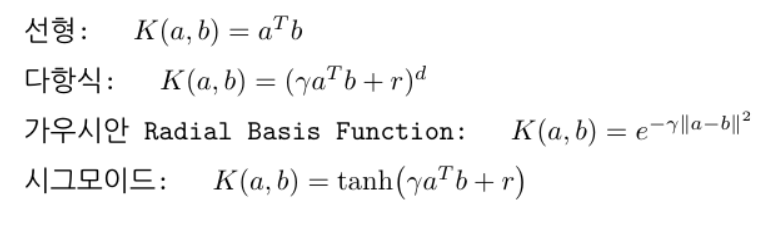지난글에 간단히 SVM이 무엇인지, 우리가 문제를 어떻게 formulation해야 하는지를 살펴보았다.
기존의 constrained optimization문제를 unconstrained optimization으로 풀수있게 해주는 놀라운 발견을 예시로 잠시 살펴보겠다.
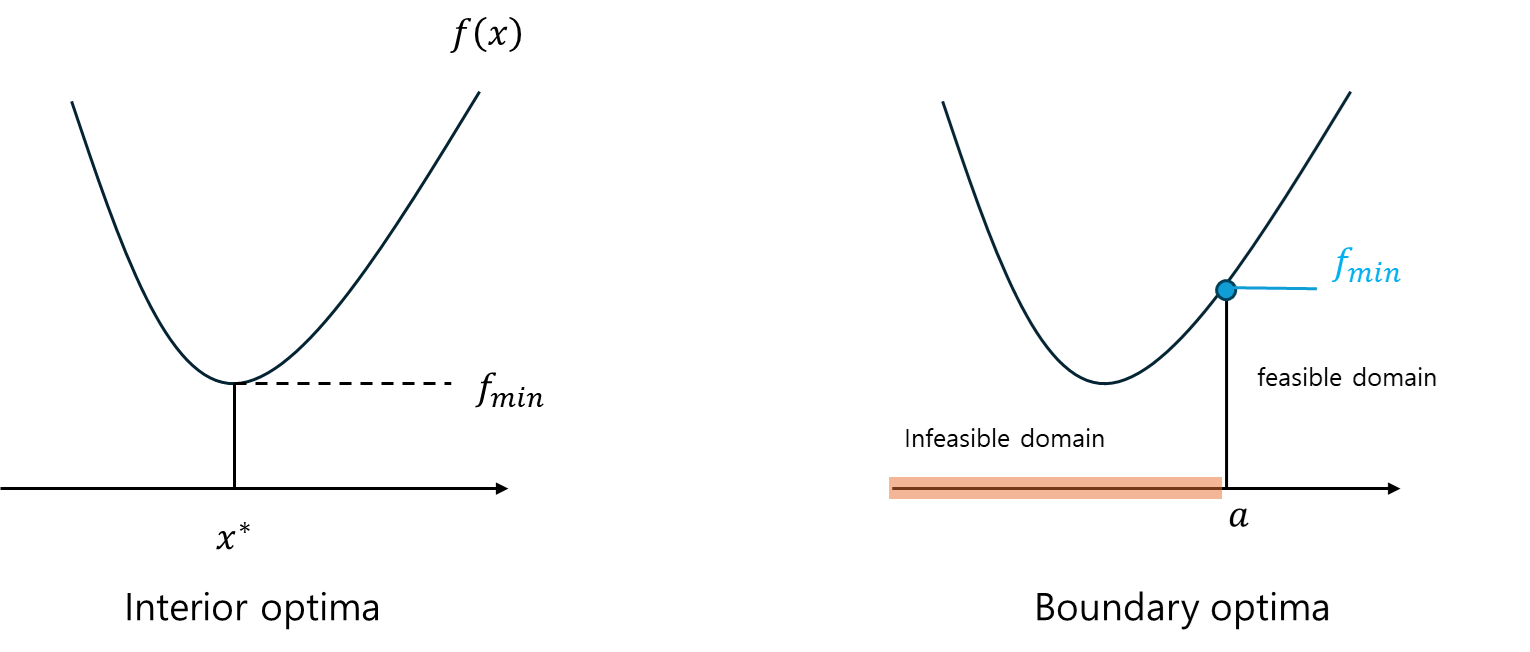
쉽게 생각하기 위해 1D 그래프를 보자.f ( x ) f(x) f ( x ) ( − ∞ , + ∞ ) (-\infin,+\infin) ( − ∞ , + ∞ ) Interior optima 라고 한다.
그런데, 어느순간 우리가 x x x a a a x < a x < a x < a Infeasible domain 이라 하고, x > a x>a x > a feasible domain 이라 한다.f min f_{\min} f m i n f ( a ) f(a) f ( a ) → \to → Boundary optima 라고 부른다.
⇒ \Rightarrow ⇒
그렇다면 이번글에서, constrained optimization 문제를 unconstrained optimization 문제로 풀수있게 해주는 놀라운 발견인 KKT condition 를 보자.
Augmented target function and Lagrange Multiplier
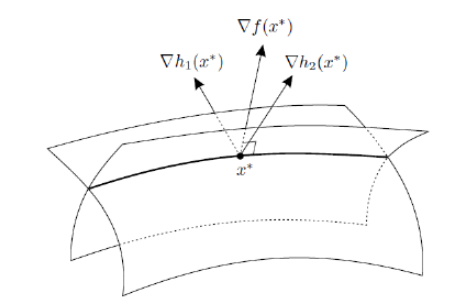
constrained가 없으면 최적해는 Convex Set의 내부에 존재하고, constrained가 존재하면 최적해는 constrained에 해당하는 hyperplane위에 존재하게 된다.
x ∗ x^* x ∗ h 1 ( x ) , h 2 ( x ) , ⋯ , h m ( x ) h_1(x),h_2(x),\cdots,h_m(x) h 1 ( x ) , h 2 ( x ) , ⋯ , h m ( x )
∇ f ( x ∗ ) + λ 1 ∗ ∇ h 1 ( x ∗ ) + ⋯ + λ m ∗ ∇ h m ( x ∗ ) = ∇ f ( x ∗ ) + ∑ i = 1 m λ i ∗ ∇ h i ( x ∗ ) = 0 T \nabla f(x^*)+\lambda _1^*\nabla h_1(x^*)+\cdots+\lambda_m^*\nabla h_m(x^*)=\nabla f(x^*)+\sum_{i=1}^m \lambda_i^*\nabla h_i(x^*) = 0^T ∇ f ( x ∗ ) + λ 1 ∗ ∇ h 1 ( x ∗ ) + ⋯ + λ m ∗ ∇ h m ( x ∗ ) = ∇ f ( x ∗ ) + i = 1 ∑ m λ i ∗ ∇ h i ( x ∗ ) = 0 T 그리고 λ i ∗ \lambda_i^* λ i ∗ Lagrange Multiplier 이라고 한다.
그래서 이게 뭔데요 하고 느낄수있지만, Lagrange Multiplier와 구속조건의 term들을 target function에 포함시키게 된다면 , Constrained optimization을 Unconstrained optimization으로 바꿔 풀수있다.
Augmented target function
l ( x , λ ) : = f ( x ) + ∑ i = 1 m λ i h i ( x ) where l : R n × R m → R l(x,\lambda) := f(x) + \sum_{i=1}^m\lambda_ih_i(x) \qquad\text{where }\;l : \mathbb{R}^n \times\mathbb{R}^m \to\mathbb{R} l ( x , λ ) : = f ( x ) + i = 1 ∑ m λ i h i ( x ) where l : R n × R m → R 위 식의 l l l
그렇다면 원래의 x x x x , λ x,\lambda x , λ x ∗ , λ ∗ x^*,\lambda^* x ∗ , λ ∗
x ∗ : x^* : x ∗ : f f f → \to → Primal variable λ ∗ : \lambda^*: λ ∗ : → \to → Dual variable
그렇다면 우리는 최적해를 구하기 위해 gradient를 구해야 할것이고, gradient를 구하면,
∇ l ( x ∗ , λ ∗ ) = ( ∂ ∂ x l ( x ∗ , λ ∗ ) ∂ ∂ λ l ( x ∗ , λ ∗ ) ) = ( ∇ f ( x ∗ ) + ∑ i = 1 m λ i ∗ ∇ h i ( x ∗ ) h ( x ∗ ) ) = 0 T \nabla l(x^*,\lambda^*) = \binom{\frac{\partial}{\partial x}l(x^*,\lambda^*)}{\frac{\partial}{\partial \lambda}l(x^*,\lambda^*)} = \binom{\nabla f(x^*)+\sum_{i=1}^m \lambda_i^*\nabla h_i(x^*)}{h(x^*)} = 0^T ∇ l ( x ∗ , λ ∗ ) = ( ∂ λ ∂ l ( x ∗ , λ ∗ ) ∂ x ∂ l ( x ∗ , λ ∗ ) ) = ( h ( x ∗ ) ∇ f ( x ∗ ) + ∑ i = 1 m λ i ∗ ∇ h i ( x ∗ ) ) = 0 T 이 된다. 이러한 식을 Dual과 Primal에 대한 문제를 푼다하여 Primal Dual Problem 이라 한다.
그리고 중요한것 한가지가 있는데, l l l
이해가 잘 안될수도있으니, 역시나 예제를 살펴보자
Example
min x f ( x 1 , x 2 ) = ( x 1 − 2 ) 2 + ( x 2 − 2 ) 2 sub. to h 1 ( x 1 , x 2 ) = x 1 2 + x 2 2 = 1 \underset{x}{\min} \quad f(x_1,x_2) = (x_1-2)^2+(x_2-2)^2\\ \text{sub. to} \quad h_1(x_1,x_2)=x_1^2+x_2^2=1 x min f ( x 1 , x 2 ) = ( x 1 − 2 ) 2 + ( x 2 − 2 ) 2 sub. to h 1 ( x 1 , x 2 ) = x 1 2 + x 2 2 = 1 이 문제를 풀려면, 위의 과정을 그대로 진행하면 된다.
Augmented target function 만들기l ( x , λ ) = ( x 1 − 2 ) 2 + ( x 2 − 2 ) 2 + λ ( x 1 2 + x 2 2 − 1 ) l(x,\lambda) = (x_1-2)^2+(x_2-2)^2 + \lambda (x_1^2+x_2^2-1) l ( x , λ ) = ( x 1 − 2 ) 2 + ( x 2 − 2 ) 2 + λ ( x 1 2 + x 2 2 − 1 )
목적함수를 찾았으니, 이제 gradient를 구하면된다.
gradient 찾기( ∂ ∂ x l ( x , λ ) ∂ ∂ λ l ( x , λ ) ) = ( ∂ ∂ x ( ( x 1 − 2 ) 2 + ( x 2 − 2 ) 2 + λ ( x 1 2 + x 2 2 − 1 ) ) ∂ ∂ λ ( ( x 1 − 2 ) 2 + ( x 2 − 2 ) 2 + λ ( x 1 2 + x 2 2 − 1 ) ) ) \binom{\frac{\partial}{\partial x}l(x,\lambda)}{\frac{\partial}{\partial \lambda}l(x,\lambda)} = \binom{\frac{\partial}{\partial x}\left ( (x_1-2)^2+(x_2-2)^2 + \lambda (x_1^2+x_2^2-1)\right )}{\frac{\partial}{\partial \lambda}((x_1-2)^2+(x_2-2)^2 + \lambda (x_1^2+x_2^2-1))} ( ∂ λ ∂ l ( x , λ ) ∂ x ∂ l ( x , λ ) ) = ( ∂ λ ∂ ( ( x 1 − 2 ) 2 + ( x 2 − 2 ) 2 + λ ( x 1 2 + x 2 2 − 1 ) ) ∂ x ∂ ( ( x 1 − 2 ) 2 + ( x 2 − 2 ) 2 + λ ( x 1 2 + x 2 2 − 1 ) ) ) ∂ ∂ x 1 , ∂ ∂ x 2 , ∂ ∂ λ \frac{\partial}{\partial x_1}, \frac{\partial}{\partial x_2}, \frac{\partial}{\partial \lambda} ∂ x 1 ∂ , ∂ x 2 ∂ , ∂ λ ∂
KKT Condition: Equality Constraints와 Inequality Constraints가 모두 존재할 때 optimum의 조건
아래와 같이 equality,Inequality constraint가 둘다 존재할때는
Augmented target function을 다음처럼 정의할 수 있고,
l ( x , λ , α ) : = f ( x ) + ∑ i = 1 m λ i h i ( x ) + ∑ j = 1 l α j g j ( x ) l(x,\lambda,\alpha):=f(x)+\sum_{i=1}^m\lambda_i h_i(x)+\sum_{j=1}^l \alpha_j g_j(x) l ( x , λ , α ) : = f ( x ) + i = 1 ∑ m λ i h i ( x ) + j = 1 ∑ l α j g j ( x ) 이때의 optimum x ∗ x^* x ∗ KKT Condition 을 만족한다.
∇ f ( x ∗ ) + ∑ i = 1 m λ i ∗ ∇ h i ( x ∗ ) + ∑ j = 1 l α j ∗ ∇ g j ( x ∗ ) = 0 T (stationary) h i = 0 , g j ≤ 0 (primal feasibility) α j ≥ 0 , ( λ i ≠ 0 ) (dual feasibility) α j g j = 0 (complementary slackness) \begin{aligned} &\nabla f(x^*) + \sum_{i=1}^{m} \lambda_i^* \nabla h_i(x^*) + \sum_{j=1}^{l} \alpha_j^* \nabla g_j(x^*) = 0^T \quad \text{(stationary)} \\ &h_i = 0, \; g_j \leq 0 \quad \text{(primal feasibility)} \\ &\alpha_j \geq 0, \; (\lambda_i \neq 0) \quad \text{(dual feasibility)} \\ &\alpha_j g_j = 0 \quad \text{(complementary slackness)} \end{aligned} ∇ f ( x ∗ ) + i = 1 ∑ m λ i ∗ ∇ h i ( x ∗ ) + j = 1 ∑ l α j ∗ ∇ g j ( x ∗ ) = 0 T (stationary) h i = 0 , g j ≤ 0 (primal feasibility) α j ≥ 0 , ( λ i = 0 ) (dual feasibility) α j g j = 0 (complementary slackness) 그렇다면 이제 원래의 문제로 돌아와서, SVM일때의 구속조건은
t ( i ) ( w 0 + w T x ( i ) ) ≥ 1 t^{(i)}\left(w_0 + w^T x^{(i)} \right)\ge 1 t ( i ) ( w 0 + w T x ( i ) ) ≥ 1 이므로 SVM의 Augmented target function을 정의하면,
l ( w , w 0 , α ) : = 1 2 w T w − ∑ i = 1 m α ( i ) ( t ( i ) ( w 0 + w T x ( i ) ) − 1 ) l(w, w_0, \alpha) := \frac{1}{2} w^T w - \sum_{i=1}^{m} \alpha^{(i)} \left( t^{(i)} (w_0 + w^T x^{(i)}) - 1 \right) l ( w , w 0 , α ) : = 2 1 w T w − i = 1 ∑ m α ( i ) ( t ( i ) ( w 0 + w T x ( i ) ) − 1 ) 이 되고, optimum은 KKT Condition을 만족해야 한다.
Kernel Trick
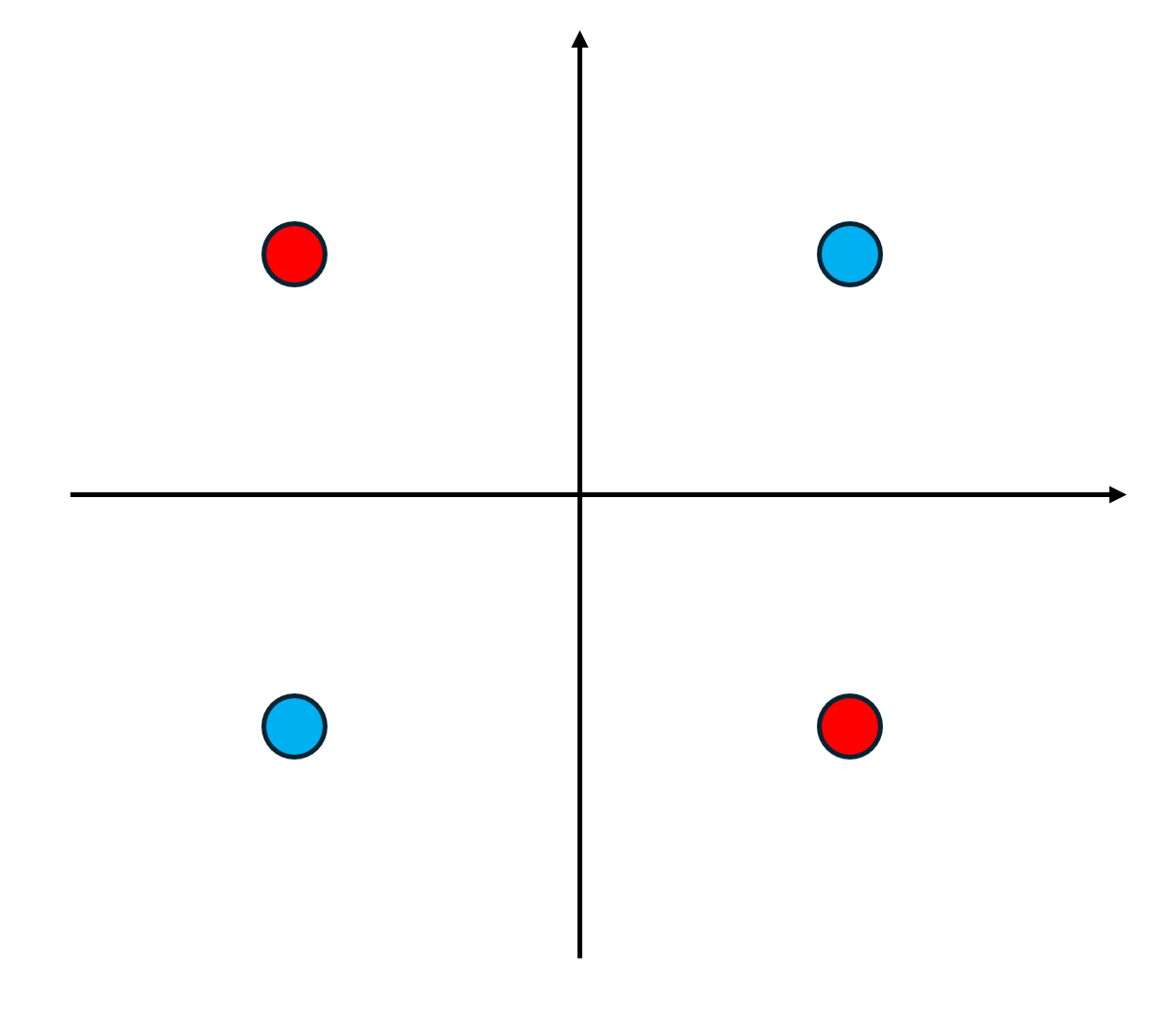
예전에 봤던 이러한 exclusive XOR문제는 single perceptron으로 절대 구분할 수 없다!→ \to →
근데 이것을 single perceptron으로 구분하게 하는 방법이 존재하는데, 이게 Kernel method이다.
(이 예제에서는 x 1 , x 2 x_1, x_2 x 1 , x 2
다음처럼 2차원 벡터를 3차원으로 mapping하는 함수
ϕ ( x ) = ϕ ( [ x 1 x 2 ] ) = ( x 1 2 2 x 1 x 2 x 2 2 ) \phi(x) = \phi \left( \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \right) = \begin{pmatrix} x_1^2 \\ \sqrt{2} x_1 x_2 \\ x_2^2 \end{pmatrix} ϕ ( x ) = ϕ ( [ x 1 x 2 ] ) = ⎝ ⎜ ⎛ x 1 2 2 x 1 x 2 x 2 2 ⎠ ⎟ ⎞ 가 있다고 하자.
그렇다면 2차원 벡터 a , b a, b a , b
ϕ ( a ) T ϕ ( b ) = ( a 1 2 , 2 a 1 a 2 , a 2 2 ) ( b 1 2 2 b 1 b 2 b 2 2 ) = a 1 2 b 1 2 + 2 a 1 b 1 a 2 b 2 + a 2 2 b 2 2 = ( a 1 b 1 + a 2 b 2 ) 2 = ( [ a 1 a 2 ] [ b 1 b 2 ] ) 2 = ( a T b ) 2 \begin{aligned} \phi(a)^T \phi(b) &= \left( a_1^2, \sqrt{2}a_1a_2, a_2^2 \right) \begin{pmatrix} b_1^2 \\ \sqrt{2}b_1b_2 \\ b_2^2 \end{pmatrix} = a_1^2b_1^2 + 2a_1b_1a_2b_2 + a_2^2b_2^2 \\ &= (a_1b_1 + a_2b_2)^2 = \left( \begin{bmatrix} a_1 & a_2 \end{bmatrix} \begin{bmatrix} b_1 \\ b_2 \end{bmatrix} \right)^2 = (a^T b)^2 \end{aligned} ϕ ( a ) T ϕ ( b ) = ( a 1 2 , 2 a 1 a 2 , a 2 2 ) ⎝ ⎜ ⎛ b 1 2 2 b 1 b 2 b 2 2 ⎠ ⎟ ⎞ = a 1 2 b 1 2 + 2 a 1 b 1 a 2 b 2 + a 2 2 b 2 2 = ( a 1 b 1 + a 2 b 2 ) 2 = ( [ a 1 a 2 ] [ b 1 b 2 ] ) 2 = ( a T b ) 2 → \to →
이를 전에 구한 Augmented target function에 대입하면, 여전히 convex한 함수이므로 똑같이 w ∗ , w 0 ∗ , α ∗ w^*,w_0^*,\alpha^* w ∗ , w 0 ∗ , α ∗ Kernel Trick 이라 한다.
일반적으로 많이 쓰는 kernel은 다음과 같다.