Support Vector Machine-1

SVM은 지금까지 보았던 교재를 보기전에, 학교 교수님의 자료를 먼저 보면서 이해해 보겠다.

---

Support Vector Machine

기존에 우리가 보았던 아달린(선형분류)이나, 로지스틱(비선형분류)의 확장이라 생각하면 된다.
그럼 어떤것이 확정되었는가?

바로 Margin이라는 영역을 갖게 된다.
교수님의 말에 따르면, decision boundary가 margin을 가지고 있다는점이 SVM의 가장 결정적인 특징이라고 생각하면된다.

SVM은 결국 무슨 문제일까?

SVM 학습은 Constrained Optimization 문제이다!

이 문제를 풀기위해, 다음 3가지를 알아보겠다.

• SVM을 이용한 선형분류기 설계 : target function과 constrained
• 다루기 어려운 constrained optimization을 이미 풀어 본 unconstrained optimization으로 만드는 방법
  $\to$ Lagrange multiplier와 Augmented target function
• Kernel trick

Linear SVM

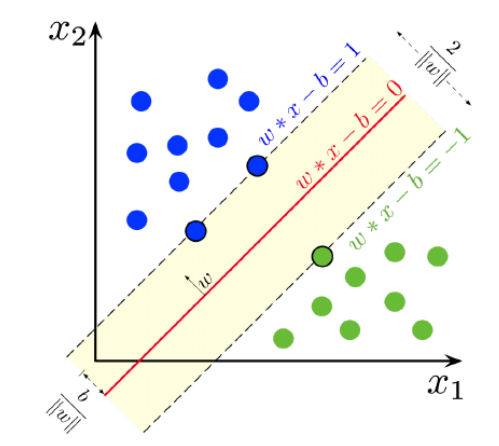
예전에 우리가 보았던 선형 분류는, 그림의 빨간색 선을 찾은것이고 즉 decision boundary이고 점선으로 표시되어 얕은 노란색인 부분이 margin이다.

SVM은 바로 이 margin을 최대화 하는 문제를 푸는것이다. 왜 margin이 필요한지 잠시 생각해보면 이전의 분류기에서는 margin이 모두 0인 경우였고, 어떤값이 들어오던 +1 or -1 (bipolar의 경우)로 나눠버린다. 이런 경우 generalize 성능이 떨어지게 되어 $E_{\text{out}}$이 커진다. 즉, 모델의 목적은 언제나 $E_{\text{out}}$를 줄여야 하므로 SVM이 생긴것이다.

그림에서 가장 가까운 파란색 샘플을 $x_{\text{pos}}$라고 하면, $x_{\text{pos}}$로부터 결정경계까지의 최단거리는

이다. 마찬가지로 가장 가까운 초록색 샘플을 $x_{\text{neg}}$라고 하면, 결정경계까지의 거리는

이다.

이 결정경계에서 가장 가까운 두 샘플을 서포트벡터라고 한다.

그렇다면 마진의 크기는 저 결정경계로부터의 최단거리를 더한

이 된다.

그리고 마진의 $+1$ 경계와 $-1$경계로부터 두 식을 빼게 된다면

가 되므로 즉 마진의 크기는

가 되고, 우리가 최대화 하려는 것이다.

Target function and Constraint

그러나, 실제로 문제를 풀때는 maximize하는것이 아닌, $\frac{2}{\left \| w \right \|} \to \underset{w,b}{\min} \frac{1}{2}w^Tw$로 바꿔 minimize하는것이 좋다.
왜그럴까? 바로 $w=0$일때 맨 처음 식에서는 $\infin$이 되기때문이다.

그런데, 이는 그렇게 쉽지 않다.
왜냐하면 우리가 간단히 보았단 예제와 다르게, sample들이 뒤죽박죽 섞여있다면, 절대 수렴하지 않는다.

따라서 이 문제를 해결하기 위해 slack variable을 데려온다.

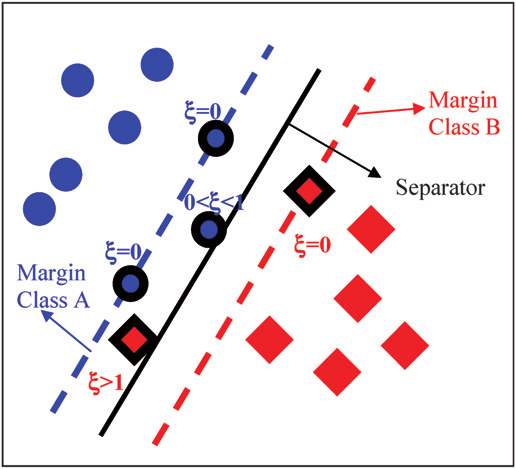
slack variable이란, 쉽게 말하면 원래 샘플의 optimum을 찾는 동안은 constraint를 뛰어넘을수 있게 해주지만, 결국 optimum에 다다랐을때는, 0가 되어 원래대로 돌아온다고 생각하면 된다.

그렇다면 원래의 문제에서 margin과 slack variable을 찾는 문제로 바뀌었는데, original optimization 문제의 관점에서 이 slack variavble 값은 0 이라는것을 기억하면 된다.

그리고 $C$라는 변수도 도입하는데, 이 $C$는 slack variable에 대해 penalty를 준다고 생각하면된다.

이해가 안될수도 있으니, 수업시간의 예제를 가져오겠다.

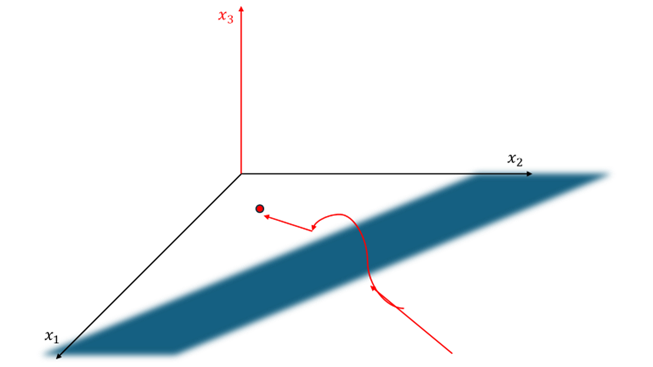
원래 기존의 $x_1, x_2$로 optimum을 찾아야된다고 하자. 그런데 저 파란색 벽이 막고있어 이런경우에는 절대 optimum을 찾지 못한다.
이 경우에 ${\color{Red}x_3}$이라는 새로운 자유도를 만들어 저 벽을 뛰어넘을수있게 한후에, optimum을 찾아갈수 있게 해주는것이 바로 slack variable이다.
그림에서도 볼수있듯이 optimum인 경우에는 slack variable, 즉 ${\color{Red}x_3} = 0$이다.

그렇다면 기존의 $\underset{w,b}{\min} \frac{1}{2}w^Tw$이 식에서,

이 식으로 바뀌게 된다.

또한 SVM에 의해 얻은 margin을 가진 hyperplane은 샘플을 정확하게 분류해야 한다는 constraint를 가진다.
이게 무슨 말이냐면, $t^{(i)}$를 우리가 어떤 샘플 $x^{(i)}$가 갖기를 원하는 target class label이라 하면,

이 되어야 한다.

이 식을 합쳐서 쓰면,

이고, slack variable을 반영해 주어야 하므로,

가 된다.

최종적으로 SVM은 다음과 같은 Constrained optimization 문제로 formulation된다.

SVM Traing

$\underset{w,b,\zeta}{\min}\quad\frac{1}{2}w^Tw + C\sum_{i=1}^m \zeta^{(i)}\\ \text{sub. to }\quad t^{(i)}\left ( w_0 + w^Tx^{(i)} \right )\ge 1-\zeta^{(i)}, \text{and }\zeta^{(i)}\ge 0 \;\;i=1,2,\cdots,m$

이제 이 최적화 문제를 어떻게 풀것인가는 다음글에 이어 작성하겠다.