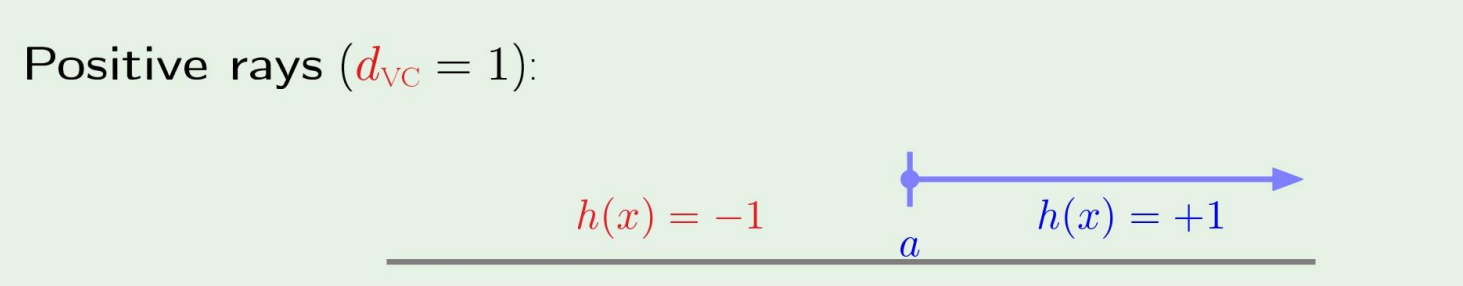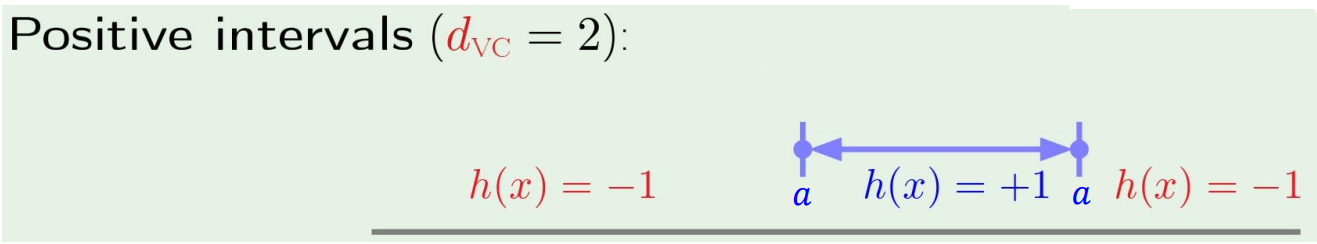저번에는 growth function을 polynomial하게 만들수있는지와, 아주 얕게 VC Inequality에 대해 보았다.
이번에는 가장 중요한 VC dimension에 대해 보겠다.
Definition of VC dimension
The VC dimension of a hypothesis set H, denoted by dVC(H), is
the largest value of N for which mH(N)=2N
즉, growth function을 설명해주는 것이다.
다르게 말하면, hypothesis가 분류할수있는 가장 많은 점의 갯수를 뜻한다.
아래의 식을 보면 이해가 빠르게 될것이다.
N≤dVC(H)⇒H can shatter Npoints
k>dVC(H)⇒k is a break point for H
이러면 당연하게도, dVC=k−1 이다.
그렇다면 저번에 우리가 growth function을 break point k에 대해
mH(N)≤i=1∑k−1(iN)
표현을 하였는데, 이 식을 VC dimension에 대해 바꾸고 싶어졌다.
mH(N)≤i=1∑dVC(iN)
왜 이렇게 되냐면, 위에서 보았듯이 k−1이 dVC이기 때문이다.
그러면 이제는 익숙한 그 세가지 예제를 살펴보자.
-
H is positive rays:
dVC=1
-
H is 2D perceptrons:
dVC=3
-
H is convex sets:
dVC=∞
VC dimension and learning
그렇다면 VC dimension은 우리에게 어떤것을 말해주는것일까?
VC dimension을 통해 bound된다는것은
dVC(H) is finite⇒g∈H will generalize
다음과 같은 의미를 지닌다.
근데 VC dimnesion에 대해서 중요한 몇가지를 생각해야된다.
VC dimenstion은
-
Independent of the learning algorithm
-
Independent of the input distribution
-
Independent of the target function
하고, 그림에서 진하게 표시된 부분에만 dependent하다.
VC dimension of perceptrons
이제 퍼셉트론으로 예시를 들면서 한가지 생각을 해볼것이다.

이러한 2D perceptron이 있을때, dVC는 k-1이므로 3이다.
여기까지는 설명했기때문에 명확하다.
근데, 차원 d=2인데, dVC=3 이다.
그렇다면, 과연 dVC=d+1일까?라는 생각을 할수있다.
이를 증명하기 위해서,
dVC≤d+1dVC≥d+1
이 두식을 모두 만족한다면, 우리는 dVC=d+1이라고 말할수있다!
이제 증명을 해보자.
먼저, d차원 벡터 x가 존재한다 가정하면, 그림과 같이 d+1개의 N이 된다.
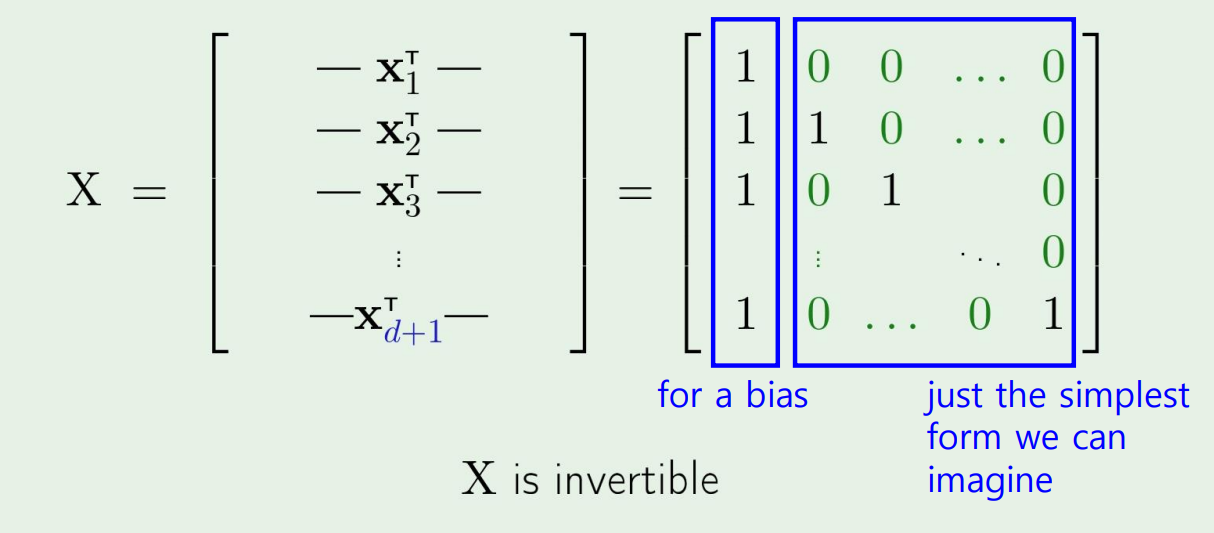
그리고 이 X에 어떤 weight를 곱해서, 우리가 y를 다음처럼 +1,−1로 구분한다고 하자.

그러면 이 w를 찾을수있고, w=X−1y로 나타낼수있다.
이를 통해 d+1 point를 나눌수있으므로, 실제로 내 dVC≥d+1이 될것이다.
그다음, dVC≤d+1를 증명해보자
dVC가 d+2의 점을 분류하지 못한다는 것을 증명하면, 위의 식이 당연해진다.
For any d+2 points,
x1,⋯,xd+1,xd+2
차원보다 더 많은 점들이 주어지면,
xj=i=j∑aixi
이고, ai are not all zeors일때, 당연하게도 모든 점들은 linearly independent하지 않는다.
따라서 d+2개의 점에 대해서는 표현할수없다!
Proof
xj=i=j∑aixi⇒wTxj=i=j∑aiwTxi
If yi=sign(wTxi)=sign(ai), then aiwTxi>0
This forces wTxj=∑i=jaiwTxi>0
Therefore, yj=sign(wTxj)=+1
즉, 두 조건을 모두 만족하기때문에, dVC=d+1 이다.
perceptron에서 VC dimension이 d+1이라는게 무엇을 의미하는것일까?
물론 VC dimension의 내가 가를수있는 점의 갯수라는 점도 있고, 더하기
→ Number of parameters!
Degrees of freedom
이제 degrees of freedom이라는 것을 보자.
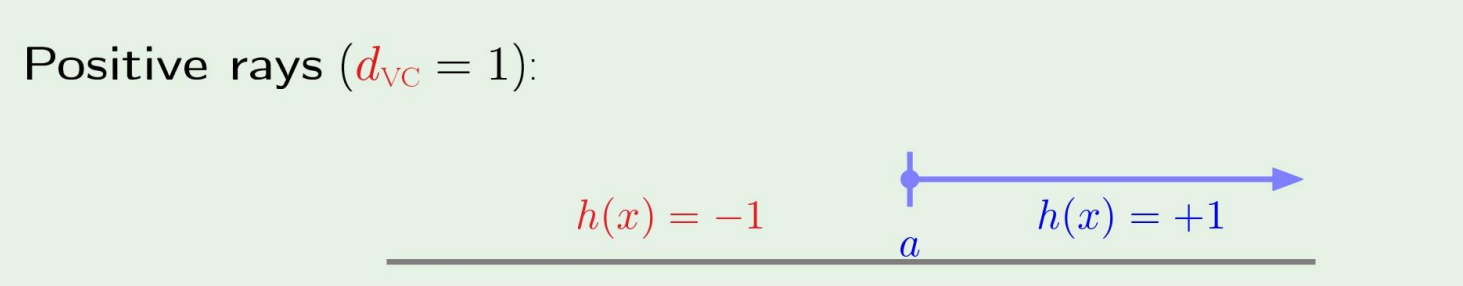
이 positive rays의 예시를 다시 보면, 내가 어떤점을 잡고, 그 점을 기준으로 갈라친다했을때, parameter의 갯수는 1이다.
→ degree of freedom is 1
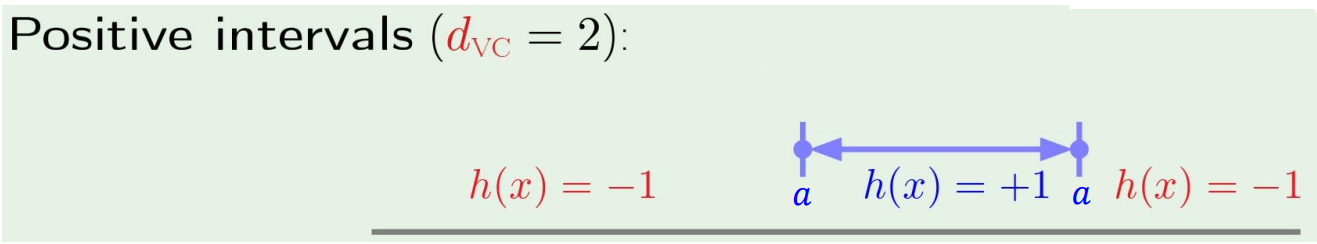
이 예시에서는 2 point를 찍어서, 구간을 정해야 하므로 number of parameter = 2이고,
→ degree of freedom is 2
그렇다면 parameter의 갯수와 degree of freedom의 갯수가 같을까?
그렇지않다!
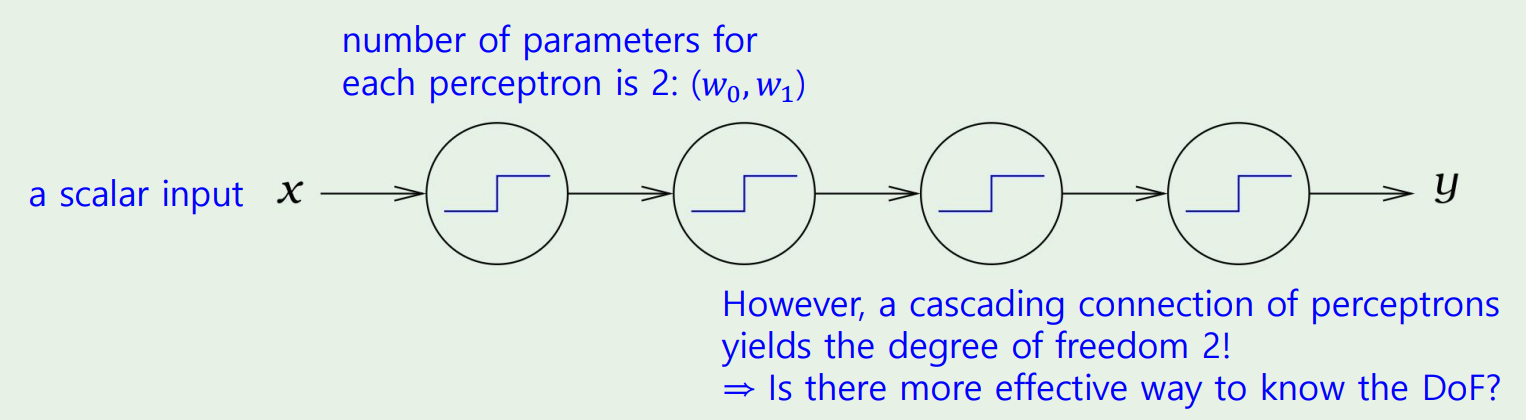
이런 cascading 형태에서는 parameter의 갯수는 계속 늘어나지만, degree of freedom에는 관여하지 않는다!