저번에는 왜 우리가 Dichotomiy라는 개념을 도입했는지, 왜 Growth function을 사용하는지를 배웠다.
잠깐 복습을 해보자.
Growth function이란, N개의 sample이 주어졌을때, 거기서부터 내가 정의할수있는 최대 dichotomiy의 갯수이다.
그리고 break point를 통해 그 값을 bound되게 만들어주었다.
이번장에는 내 growth function mH(N) 이 poliynomial하다는 것과, mH(N)이 M을 대체할수있다는 것을 증명하려 한다.
Bounding mH(N)
mH(N)이 polynomial하다는 것을 증명하기를 원한다.
우리는 이전까지
mH(N)≤⋯≤⋯≤ a polynomial
우리는 지금껏 mH(N)이 뭐보다 작다를 계속 봐왔고, 마지막처럼 나타낼수있으면 된다.
이제 우리가 하나의 function을 정의하자
이 함수는 N개의 point가 있고, break point가 k개 일때 maximum number of dichotomies를 return해주는 함수이다.
Recursive bound on B(N,k)
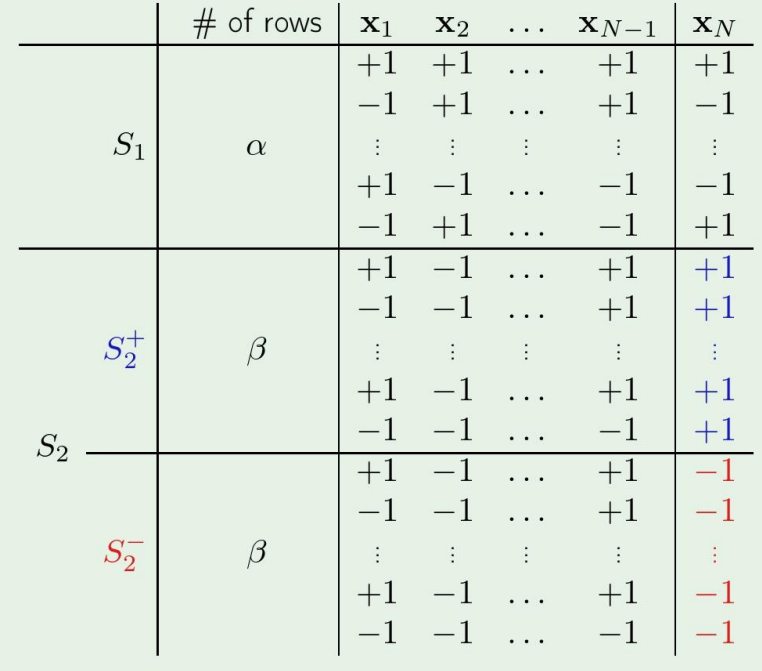
그냥 N개의 sample만 주어져있고, x1부터 xN까지 모든 가능한 조합을 전부 썼다고 생각해보자. 그리고 그 뒤에 임의로 섞어서 나온 배치가 위의 그림과 같다고 하자.
그리고 x1∼xN−1까지를 값이라고 생각하고, xN을 label이라고 생각해보겠다.
그뒤에, 이제 S2에 S1에 있던 값들을 label이 1인것과 -1인것으로 나누었다.
이경우에 break point의 개수는 B(N,k)=α+2β 이다.

이경우에는 S2−는 중복된 값이라 제거하고 본다면, N−1까지의 sample만 살펴본다하면 break point의 갯수는
α+β≤B(N−1,k)
가 된다.
그다음, β 하나에 대해서 보면
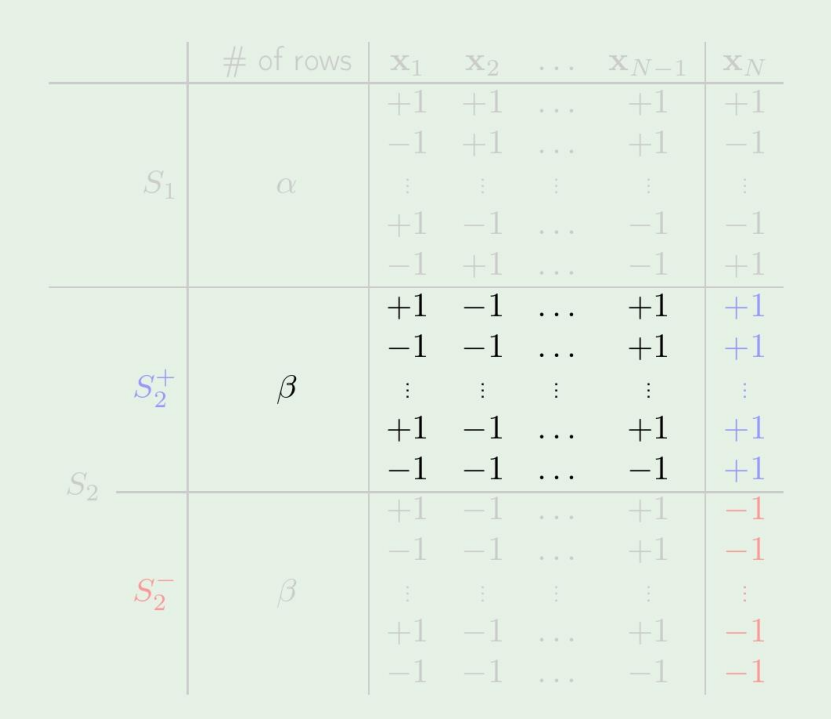
β≤B(N−1,k−1)
가 된다.
이제 위에것들을 모두 한번에 살펴보자.
B(N,k)=α+2βα+β≤B(N−1,k)β≤B(N−1,k−1)
가 되고, 그렇다면 최종적으로 다음처럼 생각할수있다.
B(N,k)≤B(N−1,k)+B(N−1,k−1)
Numerical computation of B(N,k) bound
B(N,k)를 matrix로 표현하면,
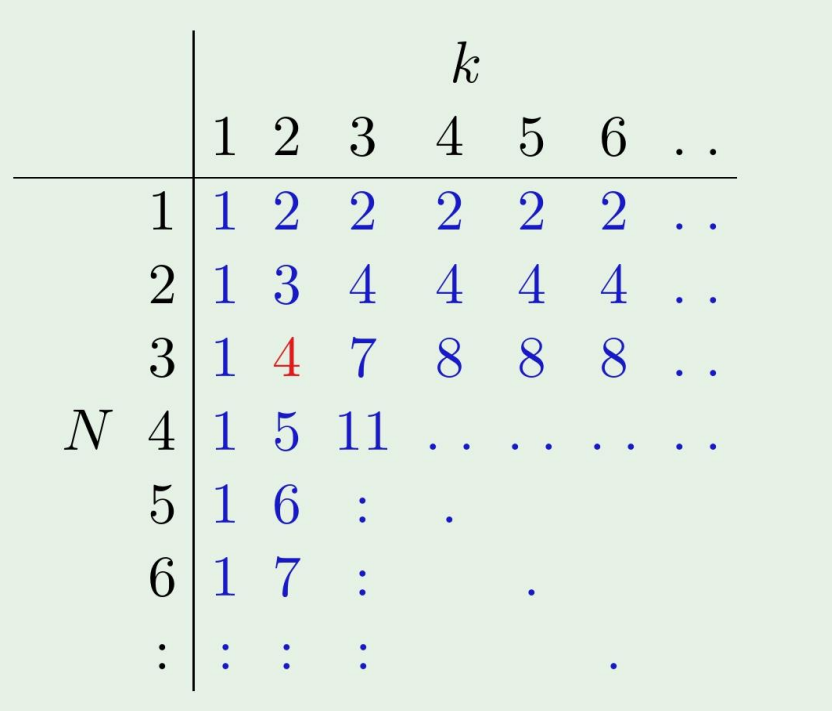
이렇게 나타나는데, 위 식에서 볼수있듯이, k와 k-1을 더하면 그 다음것이 된다.
B(N,k)≤B(N−1,k)+B(N−1,k−1)
Analytic solution for B(N,k) bound
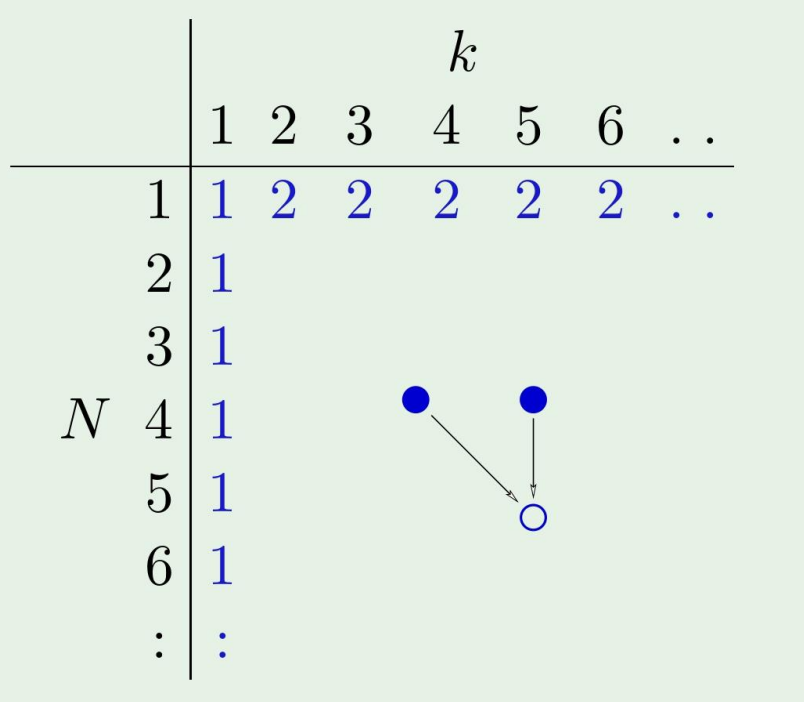
결국, 다음과 같은 Theorem이 존재하게 된다.
B(N,k)≤i=0∑k−1(iN)
결국, boundary condition이 매우 쉬워지게 된다!
Now, It is polynomial!
For a given H, the break point k is fixed
mH(N)≤i=0∑k−1(iN)
이제 다시 보았단 3가지 예제를 생각해보자
-
H is positive rays: (break point k=2)
mH(N)=N+1≤N+1
-
H is positive intervals: (break point k=3)
mH(N)=N+1≤21N2+21N+1
-
H is 2D perceptrons: (break point k=4)
mH(N)=N+1≤61N3+65N+1
mH(N) polynomial 하다는것을 모두 증명하였다.
이제 mH(N)이 M을 대체할수있다는 것을 증명하겠다.
Proof that MH(N) can replace M
우리가 원하는 식을 한번 봐보자.
P[∣Ein(g)−Eout(g)∣>ϵ]≤2Me−2ϵ2N
이 식 대신에,
P[∣Ein(g)−Eout(g)∣>ϵ]≤2mH(N)e−2ϵ2N
이걸 사용하고싶은 것이다.
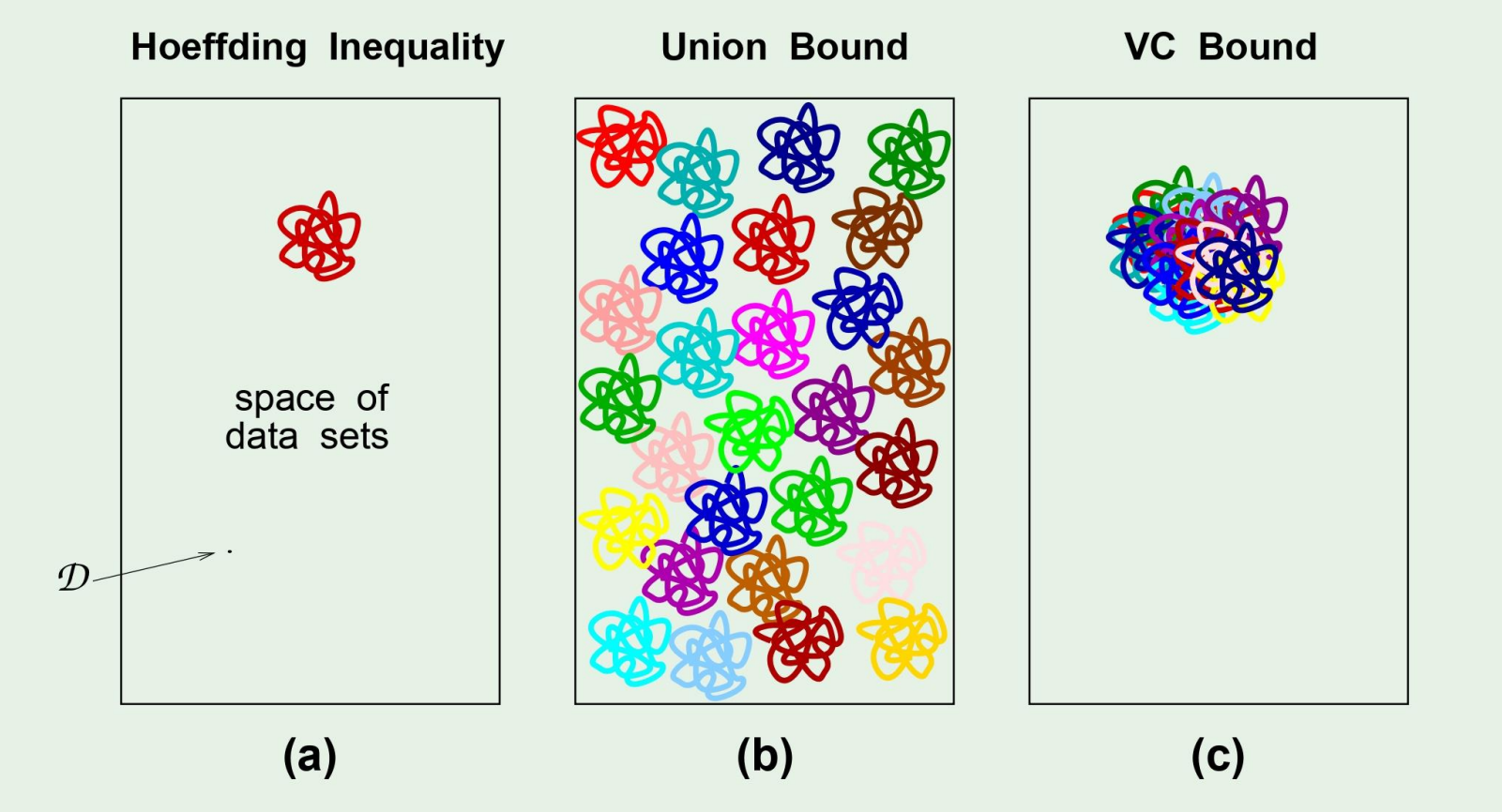
이 그림에서 저 이상한 동그라미는 bad event라고 생각하면된다.
그러면 우리가 bad event를 overlap되게 만들면 좋으므로 (c)처럼 되게 만들고싶은데, 이러한 bound를 Vapnik-Chervonenkis bound라고 한다
따라서....
P[∣Ein(g)−Eout(g)∣>ϵ]≤2mH(N)e−2ϵ2N
대신에
P[∣Ein(g)−Eout(g)∣>ϵ]≤4mH(2N)e−81ϵ2N
을 사용하고 이를 VC Inequality라고 한다.
The most important theoretical result in machine learning!
다음에는 이 VC dimension에 대해 더 자세히 살펴보겠다.






