Train versus Testing

김민재·2024년 6월 3일
ML
0

ML

목록 보기
9/17

우리의 PAC learnable한 model이 어떻게 error를 bound했는지 살펴보았다.

지금껏 우리의 호패딩 형님이 알려주었듯이,

P[∣Ein−Eout>ϵ]≤2e−2ϵ2N\mathbb{P}\left [ |E_{\text{in}} - E_{\text{out}} > \epsilon\right ] \leq 2e^{-2\epsilon^2N}

이 하나의 hypothesis에 대한 식이라고 하면, M{\color{Red} \text{M}}개의 hypothesis에 대해서는

P[∣Ein−Eout>ϵ]≤2Me−2ϵ2N\mathbb{P}\left [ |E_{\text{in}} - E_{\text{out}} > \epsilon\right ] \leq 2{\color{Red} \text{M}}e^{-2\epsilon^2N}

이 될것이다.

근데 이 M{\color{Red} \text{M}}이 ∞\infin이 되면, 결국 의미가 없어지기 때문에 우리가 이 bound를 좀더 타이트하게 잡을수는 없을까? 라고 생각할수있다.

그럼 실제로 B\mathcal{B}ad event가 발생했을때, Bn\mathcal{B}_n들은

∣Ein(hm)−Eout(hm)∣>ϵ|E_{\text{in}}(h_m)-E_{\text{out}}(h_m)| > \epsilon

이고, 다음 그림처럼 overlap이 존재한다.

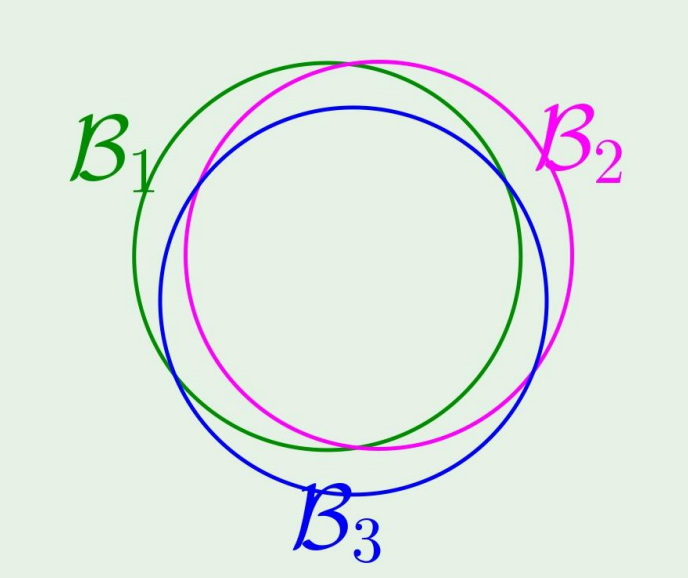
그렇다면 우리가 M{\color{Red} \text{M}}을 어떻게 improve 할수있을까?

다음 그림을 보자

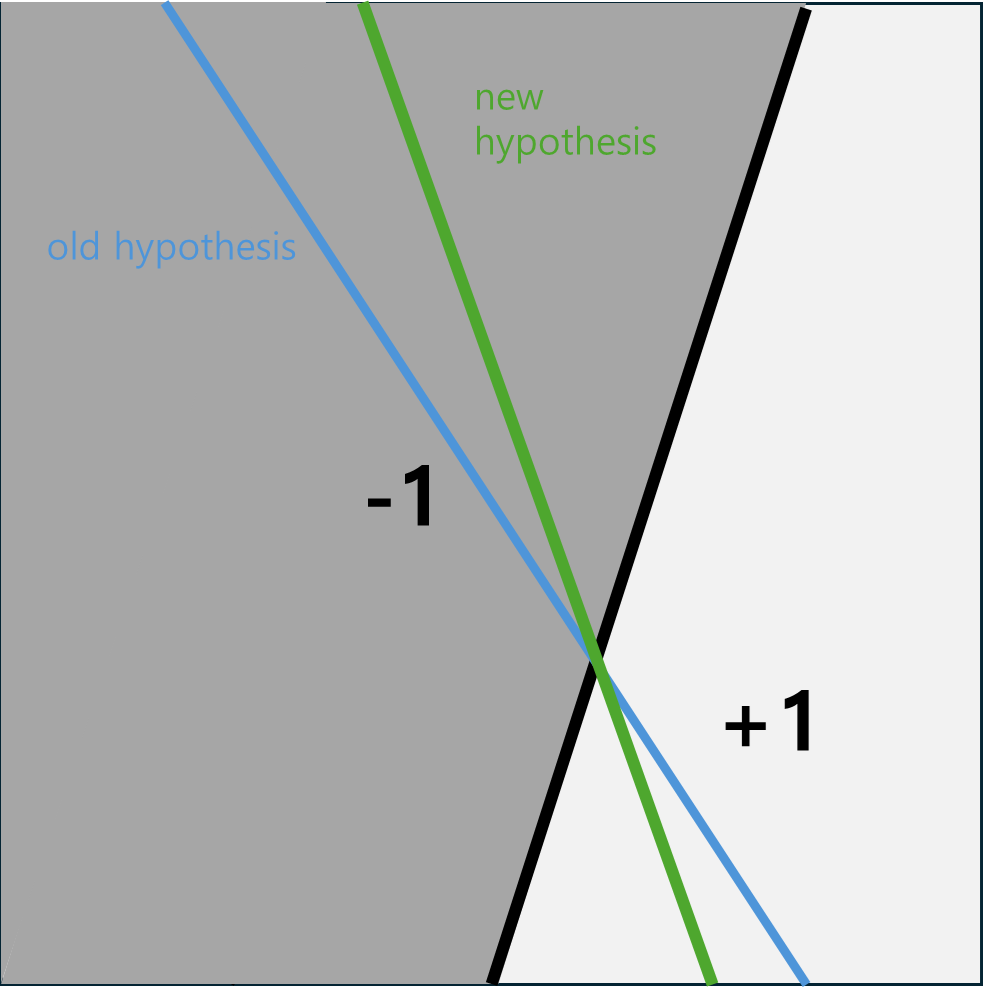
내가 그림을 좀 이상하게 그렸지만, 두 hypothesis에 대해

∣Ein(h1)−Eout(h1)∣≈∣Ein(h2)−Eout(h2)∣\left | E_{\text{in}}(h1)-E_{\text{out}}(h1) \right | \approx\left | E_{\text{in}}(h2)-E_{\text{out}}(h2) \right |

다음처럼 생각해보자.

  1. why do we care about the above?
  2. we want to figure out that the left side exceeds ϵ\epsilon when the right side does and vice versa
  3. The bad events are overlapping
  4. Hence, we can make an improvement on M!{\color{Red}\text{Hence, we can make an improvement on M!}}

What can we replace M{\color{Red}\text{M}} with?

이제 전체 공간 대신에, 우리가 finite한 set으로 point를 만들고싶으므로, (instead of the number of hypothesis)
숫자를 이제 dichotomies라는 개념을 도입하자.

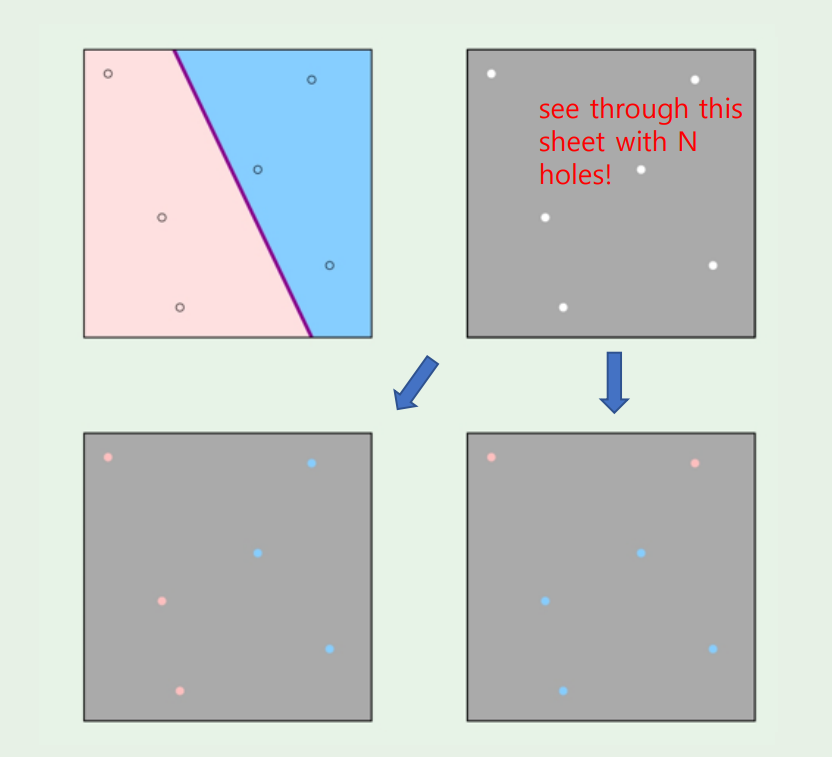
수많은 M개의 hypothesis가 있지만, 들어오는 sample에 대해 구멍이 뚫린 회색종이로 가려놓고, 분홍색과 파란색이 어떻게 되는지를 살펴보는것이다.
즉, 분홍색과 파란색을 설정하는것을 dychotomies 라고 한다.

Dichotomies: mini-hypothesis

A hypothesis h:X→{−1,+1}h : \mathcal{X} \to \left \{ -1,+1\right \}
A dichotomy h:{x1,x2,⋯ ,xN}→{−1,+1}h : \left \{ \mathbf{x}_1,\mathbf{x}_2,\cdots ,\mathbf{x}_N\right \} \to \left \{-1, +1\right \}

hypothesis ∣H∣|\mathcal{H}|의 number는 perceptron을 학습시킨다했을때 infinite이다.
그러나, 이때의 dichotomies ∣H(x1,x2,⋯ ,xN)∣\left | \mathcal{H}(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_N) \right | is at most 2N2^N

The growth function

Growth function이란, N개의 point에 대해서 최대의 dichotomy의 갯수를 count해주는 함수이다.

mH(N)=maxx1,⋯ ,xN∈X∣H(x1,⋯ ,xN)∣{\color{Red} m}_\mathcal{H}(N) = \underset{\mathbf{x}_1,\cdots,\mathbf{x}_N\in\mathcal{X}}{max}\left | \mathcal{H}(\mathbf{x}_1,\cdots,\mathbf{x}_N) \right |

그렇다면, growth function은

mH(N)≤2N{\color{Red} m}_\mathcal{H}(N) \le 2^N

를 만족하고, number of sample에 대한 함수이다.

Applying growth function - perceptrons

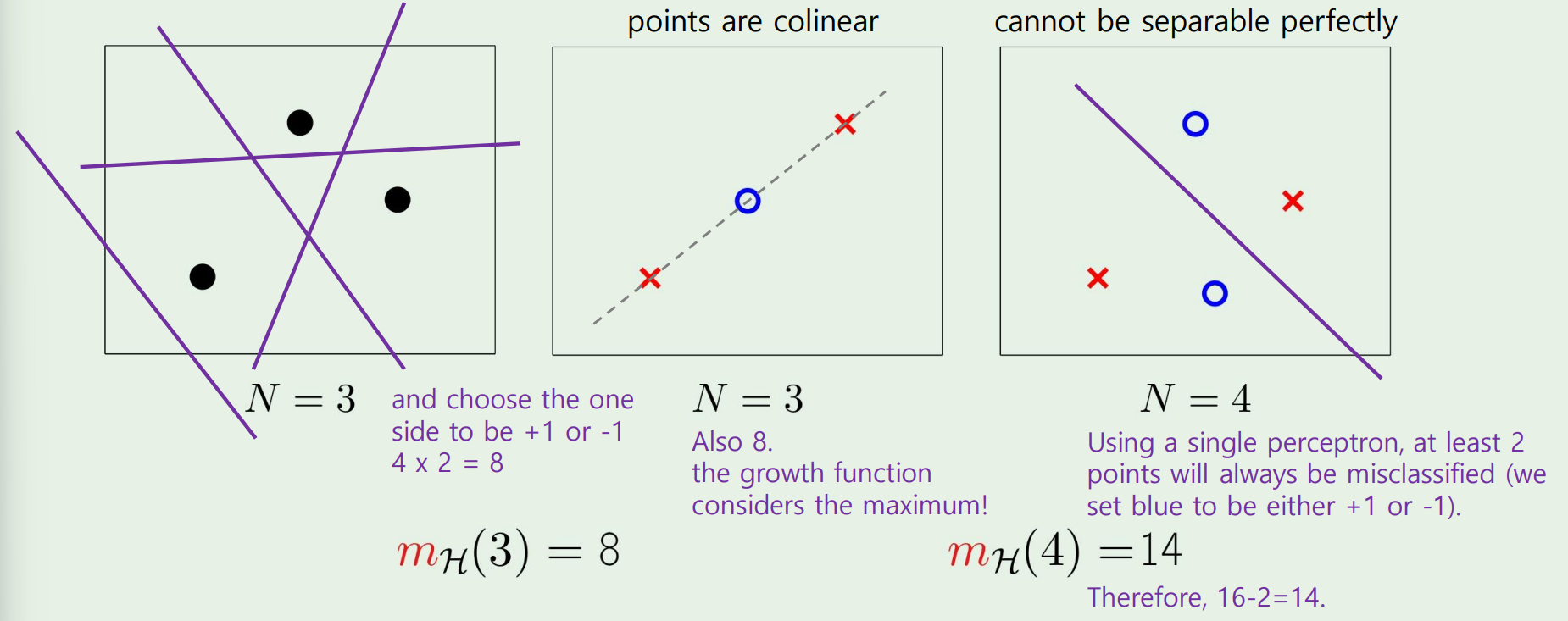
맨 왼쪽의 그림과 가운데 그림은 잠깐 생각해보면, 같은 경우라고 생각할수있다.

그런데 맨 오른쪽 샘플은 conlinear한 점이 2개씩 있기때문에 2만큼 뺀 경우의 14개이다.

여기서 우리가 알수있는점은 growth function이 bound를 정할때 항상 2N2^N으로 정의되지 않는다는것을 알수있다.

그렇다면 우리는 어떻게 그 bound식을 정의할수있을지가 궁금한 것이다.

다음의 예제들을 좀 보자

Example 1: positive rays

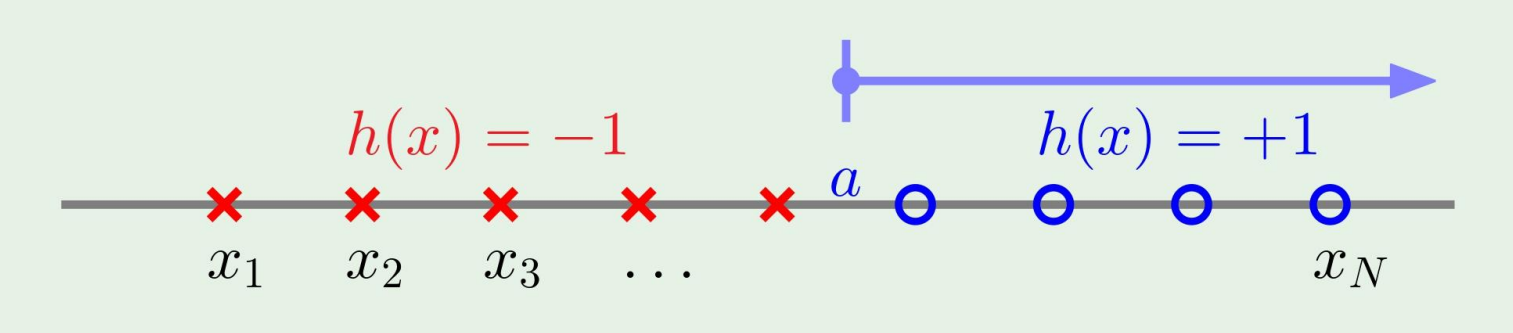
한쪽은 빨간색, 한쪽은 파란색이라고 구분하고 싶으면,
growth function은 다음처럼 된다.

mH(N)=N+1{\color{Red} m}_\mathcal{H}(N) = N+1

Example 2: positive intervals

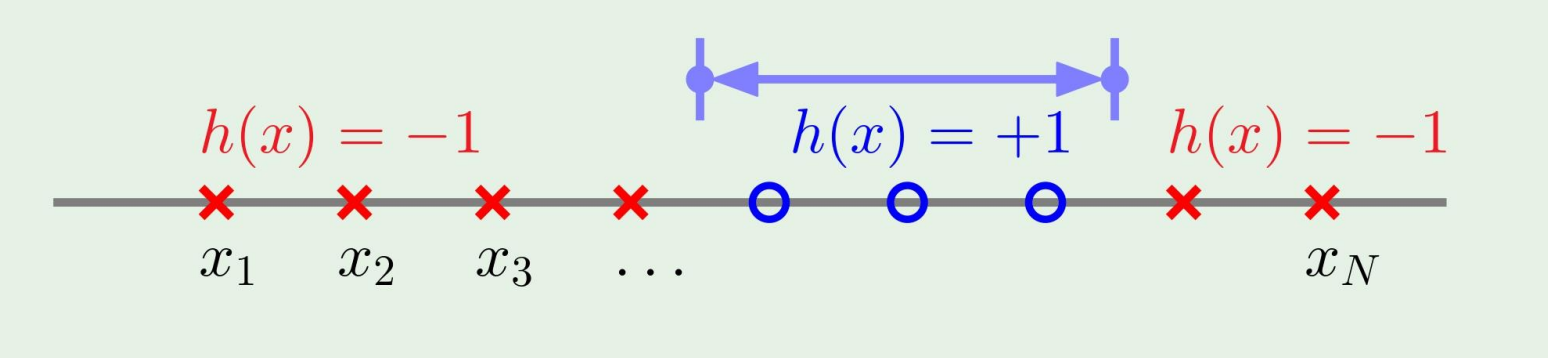
한 줄에서 어떤 간격만 우리가 파란색을 칠하고 싶다고 생각하면, N+1N+1개의 점중에 2개를 선택해야된다.

mH(N)=(N+12)+1=12N2+12N+1{\color{Red} m}_\mathcal{H}(N) = \binom{N+1}{2} + 1 = \frac{1}{2}N^2 + \frac{1}{2}N + 1

그러면 다음처럼 생각할수있다.

Example 3: convex sets

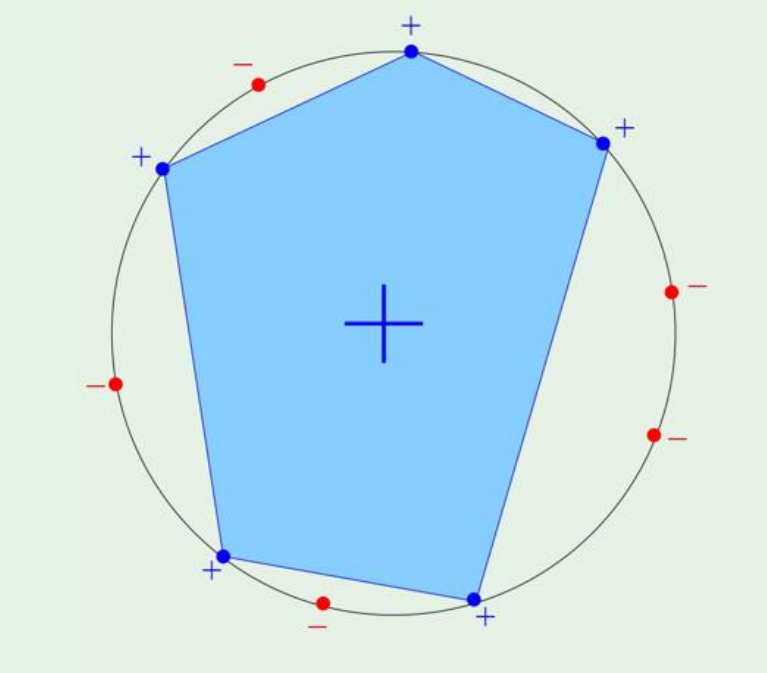
H\mathcal{H} is set of h:R2→{−1,+1}h : \mathbb{R}^2 \to \left \{ -1, +1\right \} 이다.

이때는

mH(N)=2N{\color{Red} m}_\mathcal{H}(N) = 2^N

이게 된다.
The N points are shatterd by convex sets

이제 3개의 growth function에 대해 살펴보았다.

다시 맨처음으로 돌아가보자.

Hoeffding's inequality를 기억해보자

P[∣Ein−Eout∣>ϵ]≤2Me−2ϵ2N\mathbb{P}\left [ \left | E_{\text{in}}-E_{\text{out}} \right | >\epsilon\right ]\leq 2{\color{Red} M}e^{-2\epsilon^2 N}

우리가 M{\color{Red} M}대신에 mH(N){\color{Red} m}\mathcal{H}(N)을 대체해보려했다.

근데 이제 과연 mH(N){\color{Red} m}\mathcal{H}(N)을 polynomial하게 정의할수있을까?

⇒\Rightarrow Yes! Use Break point

Break point of H\mathcal{H}

아까의 예제를 들고오자.

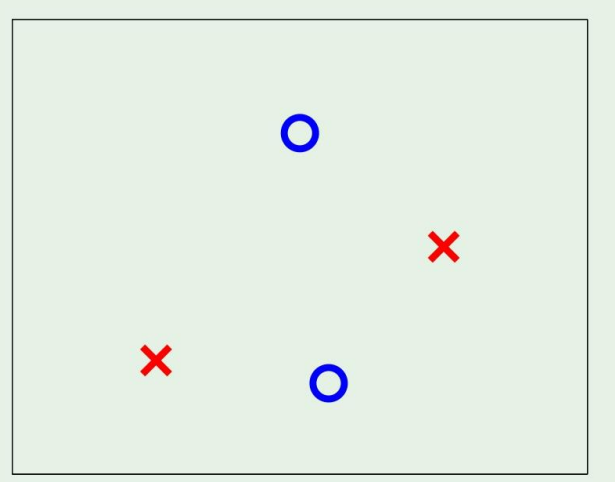
아까 이 예제에서 M을 대신할수있는 점을 가져와서 2N−2=142^N - 2 = 14라고 찾았었다

여기서 break point란 만약에 점의 갯수가 k보다 커지는 순간, 내 dichotomiy의 갯수는 2k2^k개보다 작아지게 된다.

쉽게말해서, mH(k)<2k{\color{Red} m}_\mathcal{H}(k) < 2^k가 되는 k가 바로 break point이다.

다시 아까의 3개 예제를 살펴보자

  • positive rays mH(k)=N+1{\color{Red} m}_\mathcal{H}(k) = N + 1
    break point = 2
  • positive intervals mH(k)=12N2+12N+1{\color{Red} m}_\mathcal{H}(k) = \frac{1}{2}N^2 + \frac{1}{2}N + 1
    break point = 3
  • Convex sets mH(k)=2N{\color{Red} m}_\mathcal{H}(k) = 2^N
    break point = ∞\infin

결론적으로,

No break point⇒mH(k)=2NAny break point⇒mH(k) is polynomial in N\text{No break point} \Rightarrow {\color{Red} m}_\mathcal{H}(k) = 2^N \\ \text{Any break point} \Rightarrow {\color{Red} m}_\mathcal{H}(k) \text{ is polynomial in }N

The breakpoint does exist and ti is polynomial in N{\color{Red} \text{The breakpoint does exist and ti is polynomial in N}}

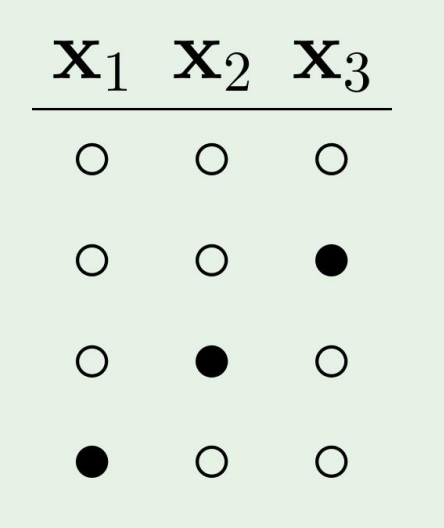
마지막으로, 이 문제에 대해서 break point가 2라고 하자.
그러면 어떻게 될지 한번 생각해보자.

그림의 예제말고 다른방법에 대해서는 어떠한 점도 break point가 존재하므로 발생할 수 없다!

profile
김민재
이전 포스트

Error and Noise

다음 포스트

Theory of Generalization

0개의 댓글