
📌 사용 환경
Python 3.10.2
conda 24.9.0
JupyterLab 4.2.5
0. RNN(Recurrent Neural Network)
지금까지 딥러닝의 기본적인 부분을 배웠다.
딥러닝 모델을 설계해봤으며, 이제 배울 것은 RNN이다.
지금까지의 ANN(Arificial NN)에서는 Activation Function을 relu를 사용했는데(CNN도 relu를 사용), 딥러닝 시계열에서는 tanh를 사용한다.
앞서 Activation Function에 여러 종류가 있다고 하여 sigmoid와 softmax, relu, tanh가 있다고 했다.
sigmoid는 0.5를 기준으로 0또는 1로, softmax는 0~1 사이의 값으로 합치면 1이 되는 비율들로 하여 가장 큰 값으로 분류,
relu는 계속한 내용과 같이 0이하(음수)는 0, 나머지(양수)는 자기 값으로.
마지막 tanh는 -1부터 1까지의 범위를 가진다. 그러면 어떻게 보면 정규화가 되는 것이다.
relu를 사용한다면 음수는 상관이 없는데 양수의 경우 자기 자신의 값을 가지다보면 무한대의 범위가 되어 버린다.
따라서 tanh를 사용하여 정규화를 하는 거라고 생각하는 것이다.
그리고 시계열이기 때문에 물론 시간단계 t가 들어간다.
참고로 신경망도 시간의 흐름을 표현하기 위해서 세로로 표현하는 경우가 많다.
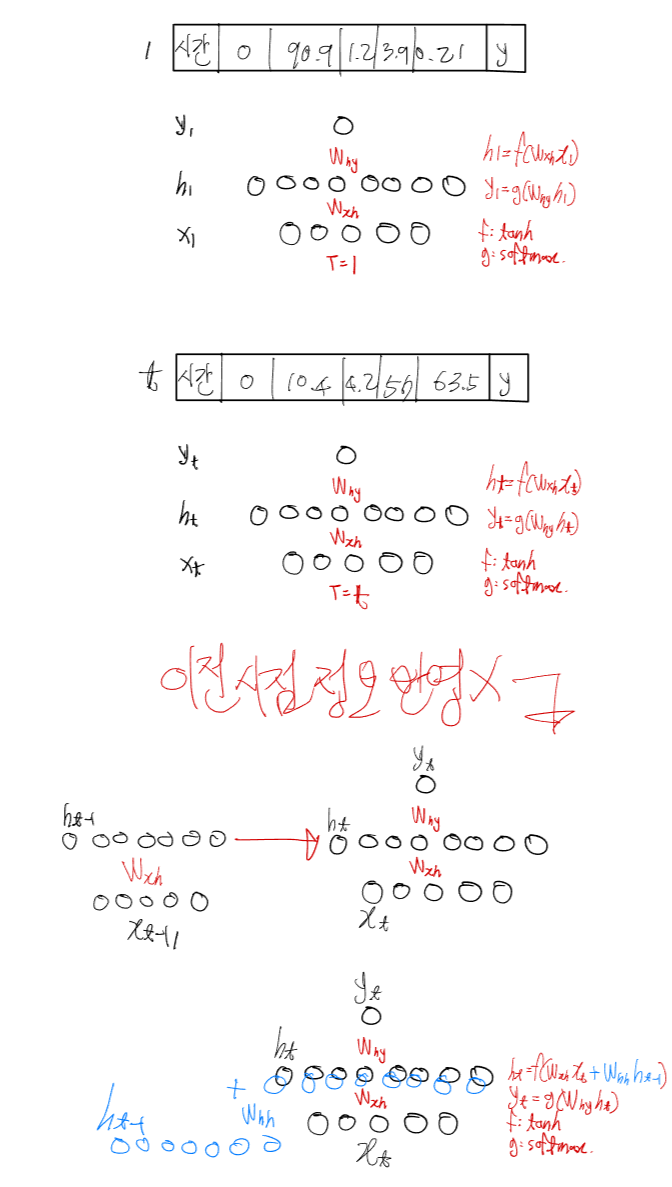
이렇게 이전 시점 정보가 반영되지 않기 때문에 이를 더해줘서 반영시키는 것이다. 이후로 히든레이어가 계속 더해진다.
그리고 이런 이전 정보들이 순환(반복)하여 입력되기 때문에
Recurrent Neural Network 라고 한다.
따라서 t-2 정보까지 반영하려면 식은 다음과 같다.
그런데 이 RNN에 문제가 생겼다.
만약 장기 과거데이터를 계속 갖고 있어서 h100 정도가 된다면, 문제가 발생한다.
앞서 말했듯, 역전파를 진행하면서 learning rate를 0.0001과 같이 줘서 곱해서 w와 b값이 새로 나오고, 그거를 다시 이용해서 순전파로 진행했었는데,
tanh는 -1에서 1의 값을 갖게끔 하는게 궁극적인 목표다.
근데 얘도 미분을하면, 0~1 사이의 값이 되어버린다.
그러면 0의 값을 가지고 되면, 빼면 업데이트가 안일어나게되어버리는 것이다.
이게 문제다.
RNN을 썼더니 3개 시점 정도면 문제가 없지만, 100시점 정도 되어버리니까 업데이트가 안일어나 버리는 것이다.
그래서 학습이 안되어 버린다.
결국에 오차 역전파에서 하는 일은 계산을 해서 learning rate와 미분 등을해서 결과적으로 업데이트를 해서 다시 또 w, b값을 가지고 순전파로 계산을 다 해서 loss가 0에 가깝게 하는게 목표인데, 100개씩 곱하다 보니까 0값이 되어버리니까 0의 값을 가지면 비용함수를 구하지 못하니까 업데이트가 안되는 문제가 발생한 것이다.
즉 지우지 말아야하는 정보를 지워버리니까 이를 방지해야했고, 그래서 나온게 LSTM이다.
1. LSTM(Long Short-Term Memory)
LSTM은 이런 장기 의존성 문제를 완화한 RNN의 개선된 모델로, Cell State()구조와 세가지의 gate를 추가한 구조다.
이 세가지 gate는
과거 정보를 기억하는 Forget gate(),
현재 정보 Input gate(),
그리고 현재 정보를 가지고 밖으로 나가는 Output gate()가 있다.
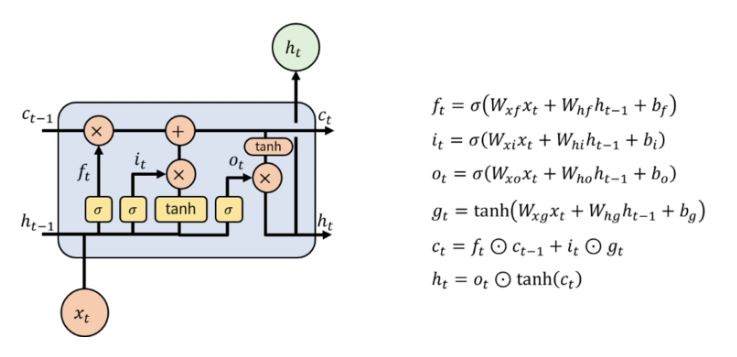
출처: https://velog.io/@aksen1317/LSTM-long-short-term-memory-GRU-Gated-recurrent-unit
이와 같은데, 결국에는 gate들은 다 시그모이드를 적용하고,
나머지는
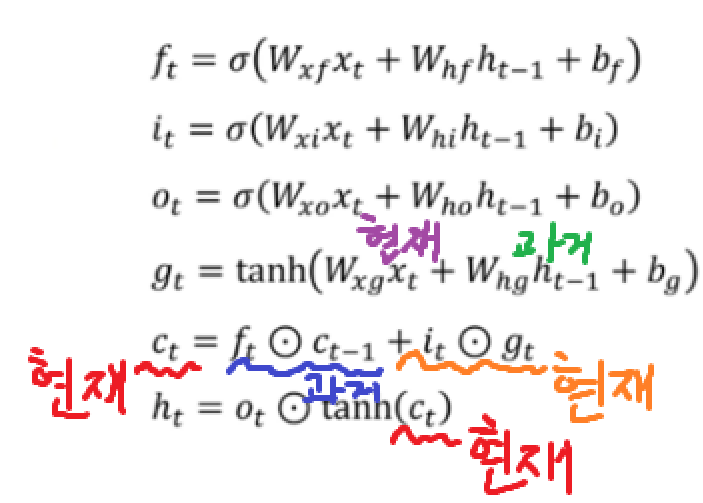
이와 같다.
이제 코드를 보자.
CNN, RNN, LSTM은 입력 데이터를 3차원 형태로 받는다.
그래서 전처리가 중요하다.
먼저 필요한 라이브러리부터 import
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rc("font", family="Malgun Gothic")
plt.rcParams["axes.unicode_minus"]=False
import tensorflow as tf
from tensorflow import keras
from keras.models import Sequential
from keras.optimizers import SGD, Adam
from keras.models import load_model
from keras.callbacks import ModelCheckpoint, EarlyStopping
from keras.callbacks import LambdaCallback
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from sklearn import metrics
import FinanceDataReader as fdr
from keras.layers import LSTM
from sklearn.metrics import r2_score, mean_squared_error, root_mean_squared_error, mean_absolute_error1.1. Sliding Window
시간 순서대로 데이터를 일정한 크기로 자르면서 이동하는 기법
데이터를 먼저 정의해주고,
data=np.array([1,2,3,4,5,6,7,8,9,10])
print(len(data))10이제 slide라는 함수를 하나 정의하여 구현해주자.
def slide(data, window):
train=[]
target=[]
for i in range(len(data)-window): # range(7)
train.append(data[i: i+window]) # data[0:3]: 123
target.append(data[i+window]) # data[3]: 4
return np.array(train), np.array(target) # 리스트로 학습을 안하기 때문에X, Y=slide(data, 3)
print(X)
print(Y)
print(X.shape, Y.shape)[[1 2 3]
[2 3 4]
[3 4 5]
[4 5 6]
[5 6 7]
[6 7 8]
[7 8 9]]
[ 4 5 6 7 8 9 10]
(7, 3) (7,)이렇게 1차원을 2차원배열로 만들었다.
이 개념을 잘알아야 계속해서 사용할 수 있다.
2. 삼성전자 주식 예측
2.1. 데이터 로드
samsung=fdr.DataReader("005930", start="2020-01-01")
print(samsung.shape)
samsung.tail()(1299, 6)| Open | High | Low | Close | Volume | Change | |
|---|---|---|---|---|---|---|
| Date | ||||||
| 2025-04-08 | 55000 | 55300 | 53300 | 53500 | 25532845 | 0.005639 |
| 2025-04-09 | 53300 | 54300 | 52900 | 53000 | 20576960 | -0.009346 |
| 2025-04-10 | 56600 | 56700 | 55000 | 56400 | 22948172 | 0.064151 |
| 2025-04-11 | 55600 | 55700 | 54800 | 55200 | 13930480 | -0.021277 |
| 2025-04-14 | 56300 | 56700 | 55800 | 56300 | 3941927 | 0.019928 |
종가(Close)를 LSTM으로 예측해보자.
우선 빈 값을 먼저 채워주자
samsung=samsung.asfreq("B", method="pad")
samsung.shape(1378, 6)seq_data=samsung[["Close"]]
seq_data.tail()| Close | |
|---|---|
| Date | |
| 2025-04-08 | 53500 |
| 2025-04-09 | 53000 |
| 2025-04-10 | 56400 |
| 2025-04-11 | 55200 |
| 2025-04-14 | 56300 |
2.2. 데이터 전처리
딥러닝에서는 무조건 정규화를 시켜줘야 빠르다.
min_max_scaler=MinMaxScaler()
min_max_scaled=min_max_scaler.fit_transform(seq_data)
train, test = train_test_split(min_max_scaled, test_size=0.2, shuffle=False)
train.shape, test.shape((1102, 1), (276, 1))2.3. Sliding Window
def slide(data, window):
train=[]
target=[]
for i in range(len(data)-window):
train.append(data[i: i+window])
target.append(data[i+window])
return np.array(train), np.array(target)X_train, Y_train=slide(train, 30)
X_train.shape, Y_train.shape((1072, 30, 1), (1072, 1))1072: 학습에 사용할 총 시계열 조각 수, 샘플 수
30: 각 조각이 과거 며칠짜리인지, 시퀀스 길이, 타입스텝 수
1: 종가 Close로 특성 수
train은 정규화된 종가 데이터가 쭉 있는 배열이다.
이걸 slide() 함수로 쪼개서 0.1, 0.11, ..., 0.4 -> 타겟: 0.41 이런식으로
30일 간의 가격 -> 다음 날 가격 예측이라는 패턴을 슬라이딩 윈도우로 만들어서 쌓는 것이다.
그리고 2차원이 아닌 3차원인 이유는,
RNN 계열 모델은(LSTM 등) 입력을 (batch_size, time_steps, features)로 기대하여,
batch_size에 한번에 학습에 들어갈 샘플 수를 지정하고 (1072)
time_steps에 각 샘플이 가진 시퀀스 길이(30일)
features에 각 시점의 feature 수 (종가)가 된다.
그래서 자연스럽게 slide함수가 리턴한 배열은 3차원이 되는 거고, 모델에 바로 넣을 수 있는 구조가 된다.
2.4. LSTM 모델 학습
model=keras.Sequential()
model.add(keras.layers.Input(shape=(30, 1)))
# LSTM이 여러개면, 마지막에만 False(디폴트, 생략가능) 나머지(위)는 True
# model.add(keras.layers.LSTM(64, activation="tanh", return_sequences=True))
model.add(keras.layers.LSTM(16, activation="tanh", return_sequences=False))
model.add(keras.layers.Dense(1))
model.summary()Model: "sequential"┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ lstm (LSTM) │ (None, 16) │ 1,152 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense (Dense) │ (None, 1) │ 17 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 1,169 (4.57 KB)
Trainable params: 1,169 (4.57 KB)
Non-trainable params: 0 (0.00 B)model.compile(optimizer="adam", loss="mean_squared_error", metrics=["mse"])def on_epoch_end_fun(epoch, logs):
if(epoch + 1) % 20 == 0:
print(f"Epoch {epoch+1}: loss={logs['loss']:.4f}, mse={logs['mse']:.4f}")
print_callback=LambdaCallback(on_epoch_end=on_epoch_end_fun)
stopping_callback=EarlyStopping(monitor="loss",
patience=10, # 보통 10 정도로 지정해줌(데이터 적으면 5, 많으면 20~30 정도)
verbose=1,
restore_best_weights=True)model.fit(X_train, Y_train, epochs=100, batch_size=16, verbose=0, shuffle=False, callbacks=[print_callback, stopping_callback])Epoch 20: loss=0.0014, mse=0.0014
Epoch 40: loss=0.0009, mse=0.0009
Epoch 60: loss=0.0008, mse=0.0008
Epoch 80: loss=0.0007, mse=0.0007
Epoch 100: loss=0.0006, mse=0.0006
Restoring model weights from the end of the best epoch: 100.
<keras.src.callbacks.history.History at 0x164f7732530>shuffle을 하지 않도록 해야 배치들이 순서대로 쭉 진행하면서 다음 배치로 순서대로 w와 b값을 전달하게 된다.
2.5. 평가
X_test, Y_test=slide(test, 30)
X_test.shape, Y_test.shape((246, 30, 1), (246, 1))pred=model.predict(X_test)
r2_score(Y_test, pred)[1m8/8[0m [32m━━━━━━━━━━━━━━━━━━━━[0m[37m[0m [1m0s[0m 40ms/step
0.9799498339678935plt.figure(figsize=(10,5))
plt.plot(Y_test, label="실제 가격")
plt.plot(pred, label="예측 가격")
plt.legend()
plt.show()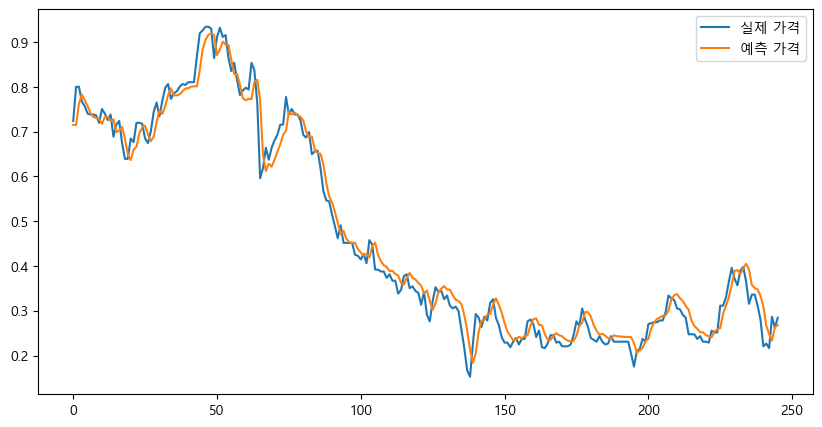
아주 잘 맞췄다.
그렇다면 이제 이 최근 30일 데이터를 사용해서 다음날 가격을 예측해보면,
last_seq=X_test[-1:]
print(last_seq.shape)
last_seq(1, 30, 1)
array([[[0.24742268],
[0.24742268],
[0.2371134 ],
[0.24329897],
[0.23092784],
[0.23092784],
[0.22886598],
[0.2556701 ],
[0.25154639],
[0.25154639],
[0.31134021],
[0.31134021],
[0.32989691],
[0.36494845],
[0.39587629],
[0.37113402],
[0.35670103],
[0.38969072],
[0.39793814],
[0.36494845],
[0.31546392],
[0.33608247],
[0.33608247],
[0.31134021],
[0.28041237],
[0.22061856],
[0.22680412],
[0.21649485],
[0.28659794],
[0.26185567]]])이렇게 가장 마지막의 30행의, 1열로 구성되어있는 Close데이터를 가져왔다.
pred=model.predict(last_seq)
pred[1m1/1[0m [32m━━━━━━━━━━━━━━━━━━━━[0m[37m[0m [1m0s[0m 47ms/step
array([[0.268124]], dtype=float32)이렇게 예측값이 나오는데, 이렇게는 얼마인지 정확히 알 수 없기때문에 역정규화가 필요하다.
price=min_max_scaler.inverse_transform(pred)
print(f"예측 가격: {price[0][0]}원")예측 가격: 55504.01171875원이렇게 다음날 예측된 가격은 55504원이다.
마지막 데이터와 비교해보면,
seq_data.tail(1)| Close | |
|---|---|
| Date | |
| 2025-04-14 | 56300 |
이렇게 꽤 유사하게 잘 나온 것을 알 수 있다.
참고
딥러닝 모델 구축 정리
ANN
- 단층: input -> output
- 다층: input -> hidden -> output
DNN(Deep NN) - 은닉층 3개 이상
RNN
데이터를 가져와서 정제를 한 다음에
딥러닝 모델을 쌓을때 고생을 좀 하는데,
경험상 간단하게 일단 돌려보자.
- 은닉층 1개로 쌓기
- 결과보고 전체적으로 낮으면
지금까지 진행하면서 LSTM에서
가중치를 저장할 수 있다.
3. 마트 가격 예측
앞서 기저귀 관련하여 마트 가격 예측을 했던 부분에서 코드를 다시 실행해서 csv파일로 저장해왔다.
이를 사용한다.
3.1. 데이터 불러오기
mart=pd.read_csv("./data/mart_diaper.csv")
mart| 구매일 | 구매금액 | |
|---|---|---|
| 0 | 2019-01-01 | 3051240 |
| 1 | 2019-01-02 | 2556280 |
| 2 | 2019-01-03 | 2729480 |
| 3 | 2019-01-04 | 2238440 |
| 4 | 2019-01-05 | 2478680 |
| ... | ... | ... |
| 580 | 2020-08-03 | 3075900 |
| 581 | 2020-08-04 | 4010200 |
| 582 | 2020-08-05 | 2937800 |
| 583 | 2020-08-06 | 2647000 |
| 584 | 2020-08-07 | 1022300 |
585 rows × 2 columns
mart.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 585 entries, 0 to 584
Data columns (total 2 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 구매일 585 non-null object
1 구매금액 585 non-null int64
dtypes: int64(1), object(1)
memory usage: 9.3+ KB우선은 object형으로 되어있기 때문에, datetime으로 바꿔준 후,
구매일 컬럼을 인덱스로 지정해준다.
mart["구매일"]=pd.to_datetime(mart["구매일"])
mart.set_index("구매일", inplace=True)
mart.head()| 구매금액 | |
|---|---|
| 구매일 | |
| 2019-01-01 | 3051240 |
| 2019-01-02 | 2556280 |
| 2019-01-03 | 2729480 |
| 2019-01-04 | 2238440 |
| 2019-01-05 | 2478680 |
3.2. 데이터 전처리
학습, 검증, 테스트 -> 순서 유지 해야 함
과거 시점(time steps) 며칠을 기준으로 할 건지 -> 30, 15, 60, 1
스케일링 -> MinMaxScaler
min_max_scaler=MinMaxScaler()
min_max_scaled=min_max_scaler.fit_transform(mart)
train, test=train_test_split(min_max_scaled, test_size=0.2, shuffle=False)
train.shape, test.shape((468, 1), (117, 1))# Sliding Window
def slide(data, window):
train=[]
target=[]
for i in range(len(data)-window):
train.append(data[i: i+window])
target.append(data[i+window])
return np.array(train), np.array(target)seq_length=7
X_train, Y_train=slide(train, seq_length)
X_train.shape, Y_train.shape((461, 7, 1), (461, 1))7일과 1개의 target으로 묶인 세트가 461개가 만들어졌다.
그러면 이제 검증 데이터를 나눠야하는데, 앞서서 0.2로 split하였는데 그는 랜덤으로 뽑아서 나눠준다.
그러나 시게열의 검증 데이터는 그렇게 하면 안된다.
랜덤이면 안되기 때문에 검증 데이터를 수기로 나눠줘야한다.
split=int(len(X_train)*0.8) # 8:2로 나누기
print(split)
X, X_val=X_train[:split], X_train[split:]
Y, Y_val=Y_train[:split], Y_train[split:]
X.shape, X_val.shape, Y.shape, Y_val.shape368
((368, 7, 1), (93, 7, 1), (368, 1), (93, 1))3.3. 모델 구성 및 학습
## 모델 구성 및 학습
model=keras.Sequential()
model.add(keras.layers.Input(shape=(seq_length, 1))) # 입력은 7일짜리 데이터 1개
# LSTM이 여러개면, 마지막에만 False(디폴트, 생략가능) 나머지(위)는 True
# model.add(keras.layers.LSTM(64, activation="tanh", return_sequences=True))
model.add(keras.layers.LSTM(16, activation="tanh", return_sequences=False))
model.add(keras.layers.Dense(1))
model.summary()Model: "sequential_1"┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ lstm_1 (LSTM) │ (None, 16) │ 1,152 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 1) │ 17 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 1,169 (4.57 KB)
Trainable params: 1,169 (4.57 KB)
Non-trainable params: 0 (0.00 B)이제 컴파일 및 fit을 진행하면 된다.
def on_epoch_end_fun(epoch, logs):
if(epoch + 1) % 20 == 0:
print(f"Epoch {epoch+1}: loss={logs['loss']:.4f}, mse={logs['mse']:.4f}",
f"val_loss={logs['val_loss']:.4f}, val_mse={logs['val_mse']:.4f}")
print_callback=LambdaCallback(on_epoch_end=on_epoch_end_fun)
stopping_callback=EarlyStopping(monitor="val_loss",
patience=20,
verbose=1,
restore_best_weights=True)model.compile(optimizer="adam", loss="mean_squared_error", metrics=["mse"])
history=model.fit(X_train, Y_train,
epochs=300, batch_size=16, shuffle=False,
validation_data=(X_val, Y_val), # validation split이 아닌 앞에서 만든 거를 그대로 넣어주기
verbose=0, callbacks=[print_callback, stopping_callback])Epoch 20: loss=0.0113, mse=0.0113 val_loss=0.0132, val_mse=0.0132
Epoch 40: loss=0.0093, mse=0.0093 val_loss=0.0100, val_mse=0.0100
Epoch 60: loss=0.0083, mse=0.0083 val_loss=0.0087, val_mse=0.0087
Epoch 80: loss=0.0081, mse=0.0081 val_loss=0.0086, val_mse=0.0086
Epoch 100: loss=0.0080, mse=0.0080 val_loss=0.0085, val_mse=0.0085
Epoch 120: loss=0.0080, mse=0.0080 val_loss=0.0085, val_mse=0.0085
Epoch 140: loss=0.0079, mse=0.0079 val_loss=0.0084, val_mse=0.0084
Epoch 160: loss=0.0078, mse=0.0078 val_loss=0.0084, val_mse=0.0084
Epoch 180: loss=0.0077, mse=0.0077 val_loss=0.0084, val_mse=0.0084
Epoch 200: loss=0.0076, mse=0.0076 val_loss=0.0084, val_mse=0.0084
Epoch 220: loss=0.0076, mse=0.0076 val_loss=0.0084, val_mse=0.0084
Epoch 223: early stopping
Restoring model weights from the end of the best epoch: 203.
학습과 검증이 둘 다 잘 떨어지면서,
학습의 loss값이 더 낮기 때문에(0에 가깝기 때문에) 잘 된 모습이다.
3.4. 평가
plt.plot(history.history["loss"], label="학습 loss값")
plt.plot(history.history["val_loss"], label="검증 loss값")
plt.legend()
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.title("학습과 검증 loss값 비교")
plt.show()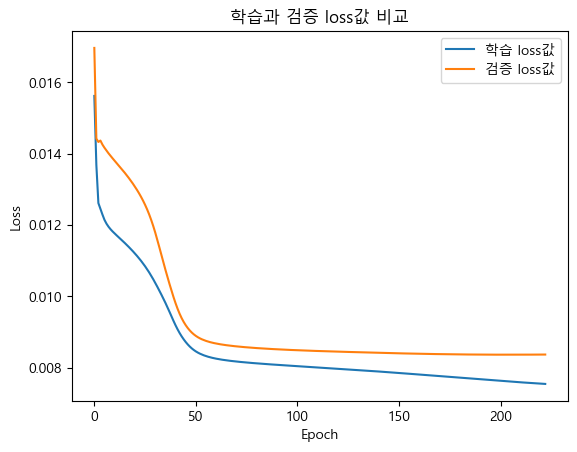
train과 검증은 잘 되었는데,
# 평가
X_test, Y_test=slide(test, seq_length)
X_test.shape, Y_test.shape((110, 7, 1), (110, 1))test_loss, test_mse=model.evaluate(X_test, Y_test)
print(f"test_loss: {test_loss:.4f}, test_mse: {test_mse:.4f}")[1m4/4[0m [32m━━━━━━━━━━━━━━━━━━━━[0m[37m[0m [1m0s[0m 11ms/step - loss: 0.0018 - mse: 0.0018
test_loss: 0.0013, test_mse: 0.0013Epoch 220: loss=0.0076, mse=0.0076 val_loss=0.0084, val_mse=0.0084
이 마지막 검증과 test가 비슷하게 나와야하는데, 현저히 낮게 나왔다.
계절성이 많이 섞여있는거 같다.
pred=model.predict(X_test)
r2=r2_score(Y_test, pred)
r2[1m4/4[0m [32m━━━━━━━━━━━━━━━━━━━━[0m[37m[0m [1m1s[0m 87ms/step
0.33580633472309196앞서 sarima에서는 음수값이 나왔었는데 조금 더 좋게 나왔지만 여전히 안좋긴하다.
plt.figure(figsize=(10,5))
plt.plot(Y_test, label="실제 가격")
plt.plot(pred, label="예측 가격")
plt.legend()
plt.show()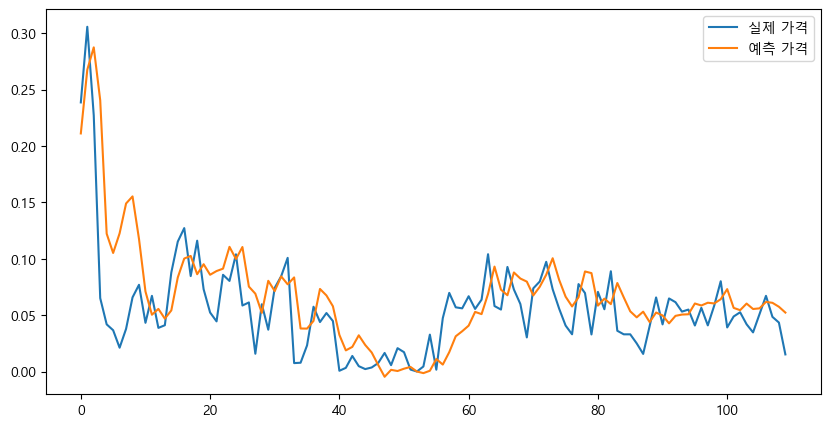
계절적인 요인을 못따라가는 모습을 보인다.
그래도 sarima보다는 잘 나왔다.
그러면 이제 최근 30일 데이터를 사용해서 다음날 가격을 예측해보자.
last_seq=X_test[-1:] # 마지막 샘플
last_seq, last_seq.shape(array([[[0.05255295],
[0.04191647],
[0.0347055 ],
[0.05088192],
[0.0671279 ],
[0.04848058],
[0.04342404]]]),
(1, 7, 1))
pred_price=model.predict(last_seq)
pred_price[1m1/1[0m [32m━━━━━━━━━━━━━━━━━━━━[0m[37m[0m [1m0s[0m 50ms/step
array([[0.05229516]], dtype=float32)# 역정규화
pred_price=min_max_scaler.inverse_transform(pred_price)
print(f"예측 가격: {pred_price[0][0]:.2f}원")
print(f"실제 가격: {mart.tail(1).values[0][0]:.2f}원")예측 가격: 3157175.00원
실제 가격: 1022300.00원4. ⭐ 모델 및 가중치 저장
참고로 프로젝트를 진행하다보면,
모델이 막 쌓여서 값이 이상하게 나올 경우가 많다.
따라서 이럴 경우를 대비해서 미리미리 모델과 가중치를 저장하는 방법이 있다.
모델 저장은 모델의 구성하는 곳 까지여서 이후 fit 과정을 진행해야하며,
가중치 저장은 fit 이후의 과정들이다.
# 모델 저장
model.save("./deep_result/mart.keras")
# 모델 불러오기
mart_load=load_model("./deep_result/mart.keras")
mart_load.summary()Model: "sequential_1"┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ lstm_1 (LSTM) │ (None, 16) │ 1,152 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 1) │ 17 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 3,509 (13.71 KB)
Trainable params: 1,169 (4.57 KB)
Non-trainable params: 0 (0.00 B)
Optimizer params: 2,340 (9.14 KB)
모델은 이렇게 진행하면 되고,
# 가중치 저장
model.save_weights("./deep_result/mart_weights.weights.h5")# 가중치 불러오기
mart_load.load_weights("./deep_result/mart_weights.weights.h5")
new_pred=mart_load.predict(X_test)
r2_score(Y_test, new_pred)[1m4/4[0m [32m━━━━━━━━━━━━━━━━━━━━[0m[37m[0m [1m0s[0m 81ms/step
0.33580633472309196그리고 반드시 가중치는 모델이 존재하는 상태에서 사용해야한다.
그래서 보통 예를들어 컴퓨터를 새로 껐다가 켰다면 다 실행하는게 아니라,
저장된 모델을 불러오고, 가중치를 불러오고, 그러면 된다.
⭐ 참고
뒷 부분이 좀 길어서 다음글에서 이어서 작성하겠다.
