안녕하세요 오늘은 머신러닝에서의 bias와 variance에 대해서 포스트 해보도록 하겠습니다.
먼저 Supervised learning의 개념에 대해서 상기해보죠. 지도학습은 모델에게 정답을 알려주고 이를 잘 맞출 수 있도록 모델을 training 시키는 것이 목표입니다.
모델은 각기 다른 input에 따라 다양한 예측값을 내놓는데, 여기서부터 bias 와 variance에 대한 설명을 시작해 보겠습니다.
Bias vs Variance
예측값들과 정답이 대체로 멀리 떨어져 있으면 결과의 bias 높다.
예측값들이 자기들끼리 대체로 멀리 흩어져있으면 결과의 variance가 높다.
위의 statement들을 잘 설명할 수 있는 그림이 있어서 가져와 보았습니다.

위의 그림에서 보시다시피,
Variance가 높은 부분은 예측값들이 각기 멀리 퍼져있고
Bias가 높은 부분은 정답(빨간색)과는 꽤나 거리가 있는 예측값들로 이루어져 있음을 알 수 있습니다.
Bias 크다 = 정답과 많이 다르다.
Variance 크다 = 많이 퍼져있다.
(확률 distribution에서도 표준편차가 큰 그래프는 멀리 멀리 퍼져있던 것을 상기시켜보자.)
다음은 Bias의 식입니다. 정답과 예측값의 평균의 차이를 제곱한 값이네요.

다음은 Variance의 식입니다. (예측값-예측값들의 평균)을 제곱 해줍니다.그리고 예측값의 수로 나눕니다.

확률분포에서 저희가 분산을 구할때 (각 데이터셋 -데이터셋의 평균)을 제곱하고 데이터 수만큼 나눠서 분산을 구했던 것과 동일한 메커니즘입니다.
자 이제 이걸 머신러닝과 연관지어봅시다.
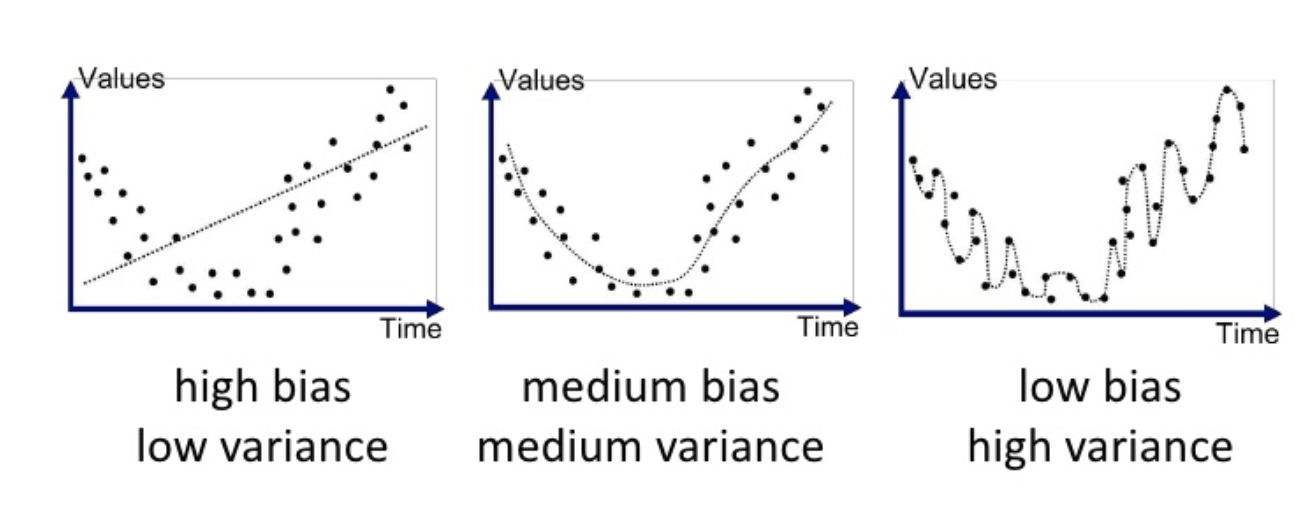
high bias low variance 그림 (맨 왼쪽)
모델이 예측을 잘 못하고 있죠. 정답값과 차이가 크게납니다.
그래서 이 모델은 high biased model 입니다. bias가 크면 Underfitting이 일어났다고도 하는데 말 그대로 Fitting이 덜 되었다고 생각하시면 될 것 같습니다.
예측모델의 분산이 셋중에 가장 작아보이죠 계산없이 직관적으로도
low bias high variance 그림 (맨 오른쪽)
예측 모델이 정답값과 거의 일치하는 모습을 보이고 있습니다. low bias이겠죠.
그래프의 변동성이 매우큽니다. 예측값이 여기저기 퍼져있죠 구불구불하게. high variance입니다.
이 모델은 Overfitting이 일어났다고도 하는데 학습을 너무 잘해서 각 데이터의 노이즈까지 학습을 해버린 경우입니다. 고차 다항식은 더 많은 계수를 가지며 이는 모델이 데이터의 미묘한 변화까지 캡쳐할 수 있고 이러한 민감성은 데이터의 노이즈나 작은 변동성에 대해서도 모델이 반응하게 만듭니다.
말 그대로 fitting이 과도하게 된거죠.
해결방법
앤드류 교수님이 제안하신 각각의 해결방법입니다.
간단명료하네요
high bias
- bigger network
- train longer
high variance
- More data
- regularization
옛날에는 trade-off 때문에 고민이 있었는데 요즘같은 big data era에는 bias만 줄일수도 있고 variance만 줄일수도 있다고 합니다.
의문점 해결
왜 꼭 고차원의 구불구불한 예측모델운 높은 분산을 가질까? 오히려 선형인게 분산이 높을 수도 있는거 아닌가? ----> 구불구불해서 high variance인게 아니다. 고차다항식이여서 high variance인거다.
(더 구불구불해도 분산이 낮을수도 있는거 맞다.)

