이번 포스트에서는 저희의 인공신경망을 더 강건하게 만들어주는 여러가지 방법들을 알아보겠습니다.

Hyperparameter tuning

하이퍼 파라미터는 모델의 학습에 있어서 아주 중요한 역할들을 합니다.

앤드류 교수님께서는 빨강-파랑-보라-초록색순으로 중요하다고 말씀해 주셨습니다.
파란색 베타는 모멘텀 상수, β1, β2 는 Adam optimizer에 쓰이는 상수이구요.
역시 parameter들을 직접적으로 학습시킬때 쓰이는 learning rate α가 가장 중요한걸 확인할 수 있죠.

Grid search vs Random search

이번에는 하이퍼파라미터들을 설정하는 방법론에 대해서 이야기 해보겠습니다.

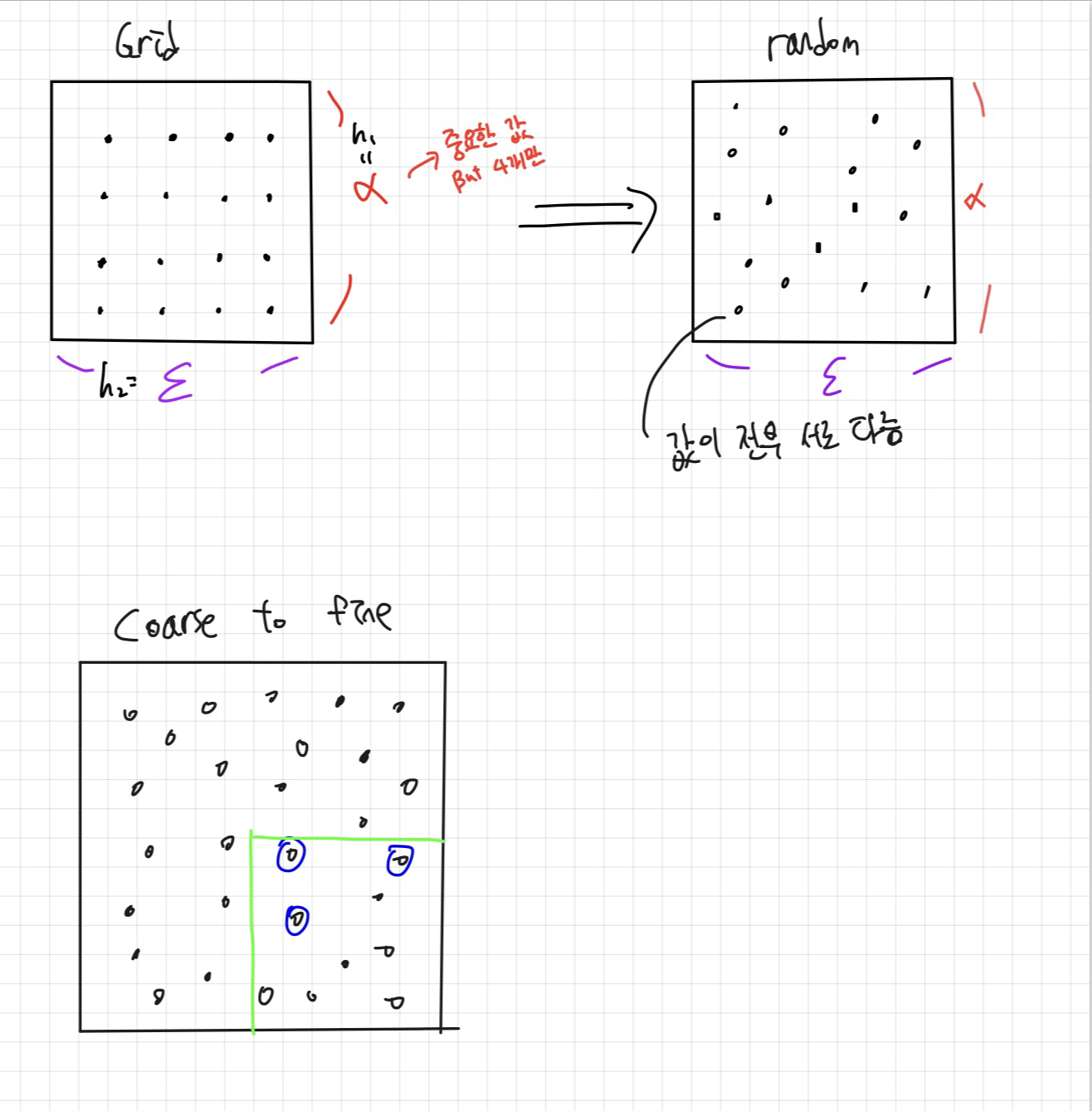
첫번째는 그림의 왼쪽위에 있는 grid search 방식입니다. 가로세로 5등분에서 규칙적으로 hyperparameter들을 고른 것을 확인할 수 있죠. 매우 이상적이여 보이지만 몇가지 문제점들이 존재합니다.

1. 비효율적인 탐색공간 활용

그리드 서치는 모든 하이퍼파라미터가 동등하게 중요하다고 가정하고 동일한 밀도로 탐색 공간을 커버합니다.
하지만 실상은 그렇지 않은경우가 허다하죠.
그림에서 하이퍼파라미터 두개중 하나는 learnig rate고 하나는 layer의 수라고 가정해봅시다.
그리드 서치의 경우 시도해 볼 수 있는 α의 수는 4개이지만 오른쪽 그림(Random search)의 경우 16개 입니다.
훨씬 더 다양한 값들로 성능평가가 가능하죠.

2. 차원의 저주

하이퍼파라미터의 차원이 증가함에 따라, 각 차원을 충분히 탐색하기 위해 필요한 데이터 포인트의 수가 급격히 증가합니다. 예를 들어 4x4=16개 였던 점이 5차원이 되면 1024개가 되죠.
이는 탐색 공간이 넓어짐에 따라 적절한 해를 찾기 위해 필요한 계산량이 크게 증가한다는 것을 의미합니다. 우리는 이렇게 많은 계산을 수행하기 보다는 몇번의 랜덤 서치를 통해 성능을 잘 내는 하이퍼파라미터를 선택하는 방식을 선호합니다.

Coarse to fine

아래 설명된 "Coarse to Fine" 방법은 먼저 랜덤 서치를 수행하여 성능이 좋은 도메인을 식별한 다음, 해당 도메인에 집중하여 더 세밀하게 탐색하는 접근법입니다.
잘하는 애들중에 제일잘하는 애들을 고르겠다는거죠.

Using an appropriate Scale

이번엔 많은 분들이 실수 할 수 있는 부분에 대해 짚고 넘어가보겠습니다.

learning rate 알파를 0.0001 ~ 1의 scale에서 고른다고 할 때
어떻게 고르는게 가장 좋을까요?
uniform 하게 고르는게 좋아보이시나요?
직관적으론 uniform하게 고르는게 아무 문제가 없어 보이지만 이는 우리의 목적과는 다른 결과를 낳곤 합니다.

우리가 0.0001 ~ 1의 scale을 선택한 이유는 10-4~10-3 사이의 범위에선 어떻게 동작할지도 궁금하고 10-3~10-2 사이의 범위에서도 어떻게 동작하는지 궁금하기 때문입니다.
단순히 uniform하게 고르려했더라면 0~1의 범위를 선택했겠죠.

이러한 저희의 목적으로 미루어봤을때 10-1~1 scale에서 90퍼센트를 골라버리는 unifrom한 search는 옳지 않습니다. 저희는 log scale로 변환함으로써 이 문제를 해결할 것 입니다. log를 씌우면 -4~0까지의 범위로 변하게 되는데 여기서 uniform 한 search를 진행하면 저희가 아까 보고싶어 한 각 범위에 대해 동일한 관심을 줄 수 있죠.

학습의 방식

앤드류 교수님은 모델 학습 방식을 두 가지 유형으로 구분하며, 이는 각각 '판다 방식(Panda Approach)'과 '캐비어 방식(Caviar Approach)'으로 불립니다. 이러한 명칭은 자연계에서 볼 수 있는 번식 전략과 유사한 점에서 착안되었습니다.

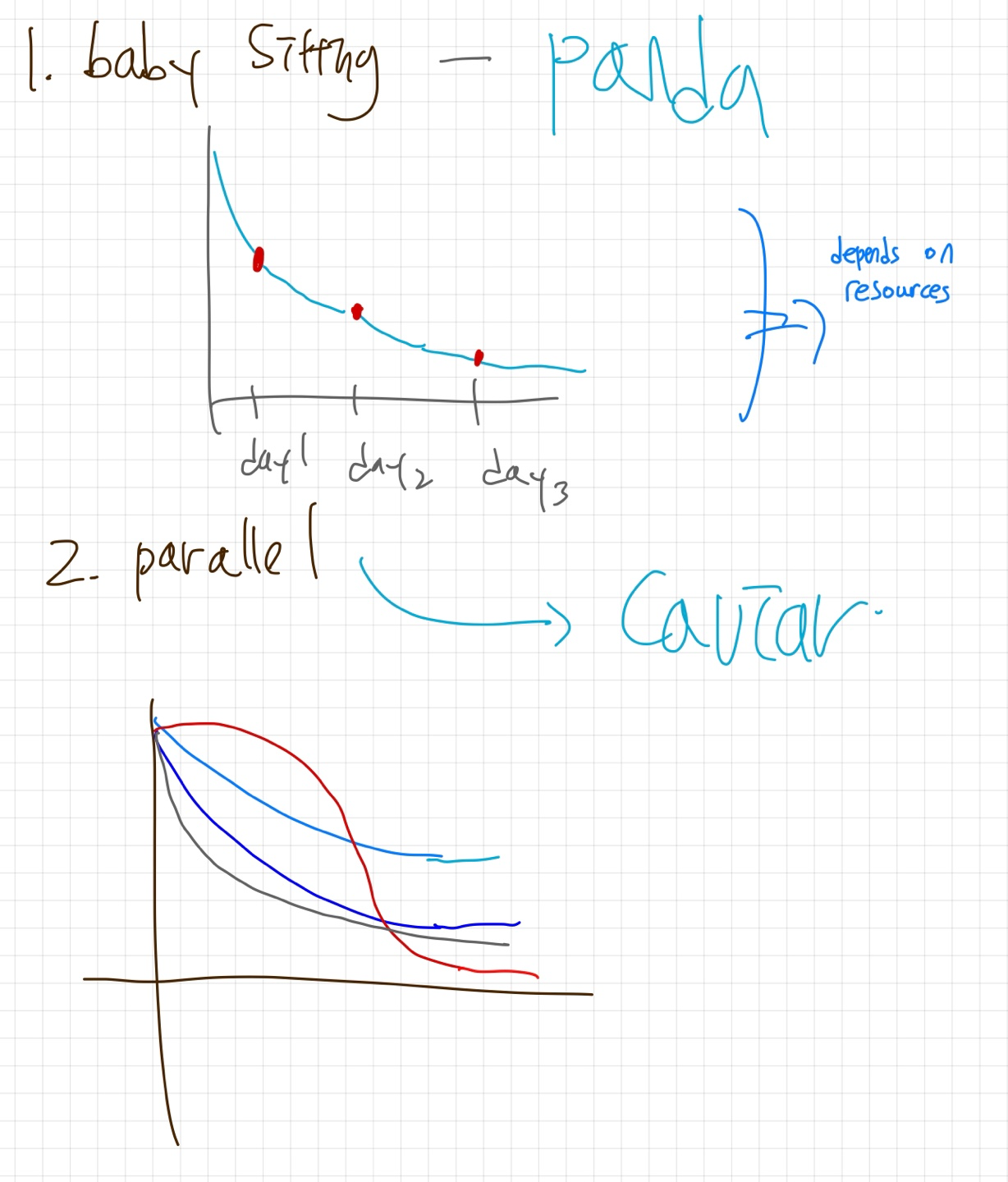
판다 방식은 어미 판다가 새끼를 매우 조심스럽게 그리고 애지중지 키우는 과정에 비유됩니다. 이 방식에서는 많은 시간, 자원, 그리고 주의를 하나의 모델 또는 소수의 모델에 집중적으로 투자하는 것을 의미합니다. 마치 판다가 자신의 새끼에게 매우 집중적인 관심과 보살핌을 제공하는 것처럼, 이 접근법은 모델 하나하나를 세심하게 조정하고 최적화하는 데 중점을 두죠.

반면, 캐비어 방식은 생선이 한 번에 많은 수의 알을 낳는 번식 전략에 빗대어 명명되었습니다. 이 방식은 대규모로 모델을 병렬로 학습시키는 접근법을 나타냅니다. 여러 모델이나 실험을 동시에 실행하여, 그 중에서 가장 성능이 좋은 모델을 선택하는 전략입니다. 이는 대량의 알 중에서 생존하는 몇몇에게만 집중하는 자연의 캐비어 전략과 유사합니다.

resource에 따라 어떤 학습방식으로 학습할지가 결정 되겠죠?

Batch Normalization

모델을 robust하게 만드는 또 하나의 방법은 BN(Batch normalization)을 적용하는 것 입니다.

아래 그림을 통해 Normalization하는게 어떻게 학습에 도움이 될지 생각해봅시다.

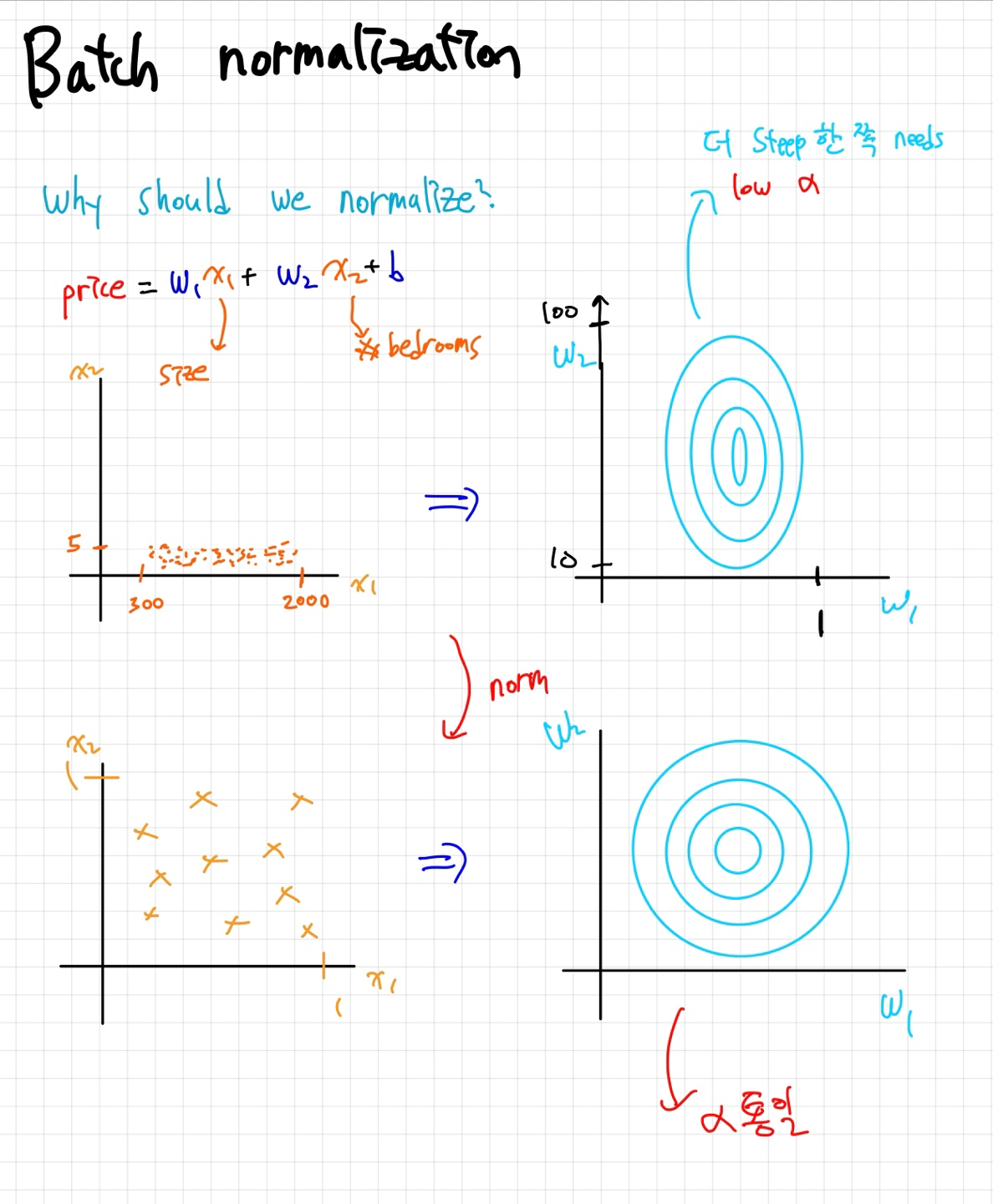
먼저 첫번째, 즉 Normalization을 하기전에는 w1,w2로 그린 loss contour plot이 오른쪽과 같이 나타납니다. 이 경우엔 문제가 생기는데요 dL/dw2 와 dL/dw1의 기울기 차이가 너무 크다는 것입니다 dL/dw1 쪽의 기울기가 훨씬 크다는 것을 쉽게 확인 할 수 있죠. (등고선이라고 생각하고 보시면 이해가 편하실 겁니다.) 이럴 경우에 w1쪽의 learning rate를 적게줘야 하는데 그러면 dw2쪽의 학습이 너무 느려집니다. 그렇다고 learnig rate를 키우면 w1이 아예 converge하지 못할 수도 있구요.

하지만 Normalization을 하면 이런문제가 해결됩니다. 같은 learning rate로 학습을 할 수 있기에 더 안정적이고 빠른 학습이 가능하죠.

Batch Norm은 n번째 layer에서 activation 함수를 통과하기 전의 값에 적용하는 것인데요.

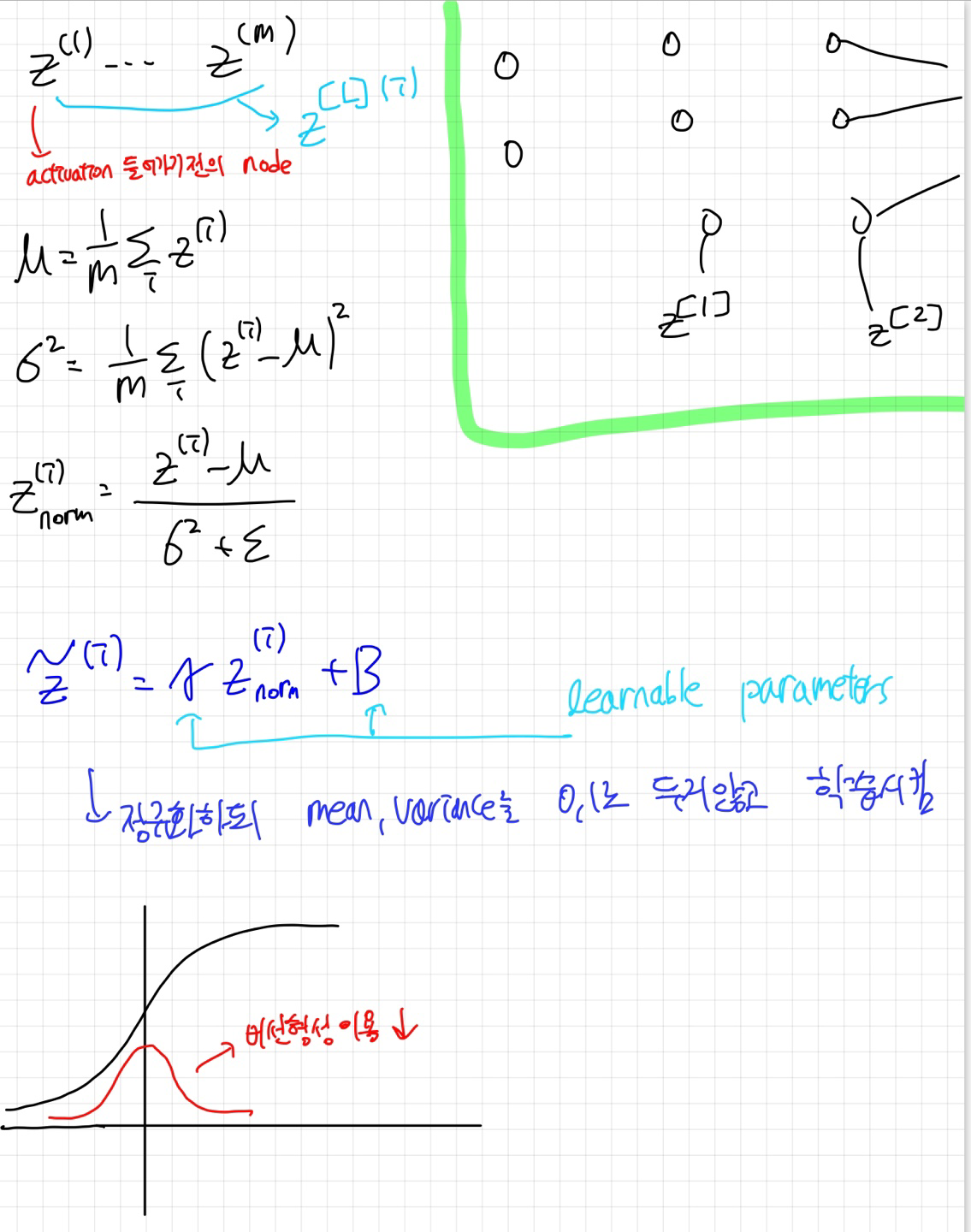
정규화 과정에서는 우선 데이터를 평균이 0이고 표준편차가 1인 정규분포, 즉 N(0,1)로 변환합니다. 이후, 모델이 학습하는 과정에서 결정되는 감마(γ) 값을 곱하고 베타(β) 값을 더함으로써, 데이터에 모델이 학습한 특정 평균과 표준편차를 적용합니다. 이렇게 함으로써, 최종적으로 데이터는 모델이 학습한 맞춤형 정규분포를 따르게 됩니다. 이 과정은 모델이 데이터의 내재된 구조를 더 잘 학습하도록 도와, 학습 과정을 효율적으로 만듭니다.

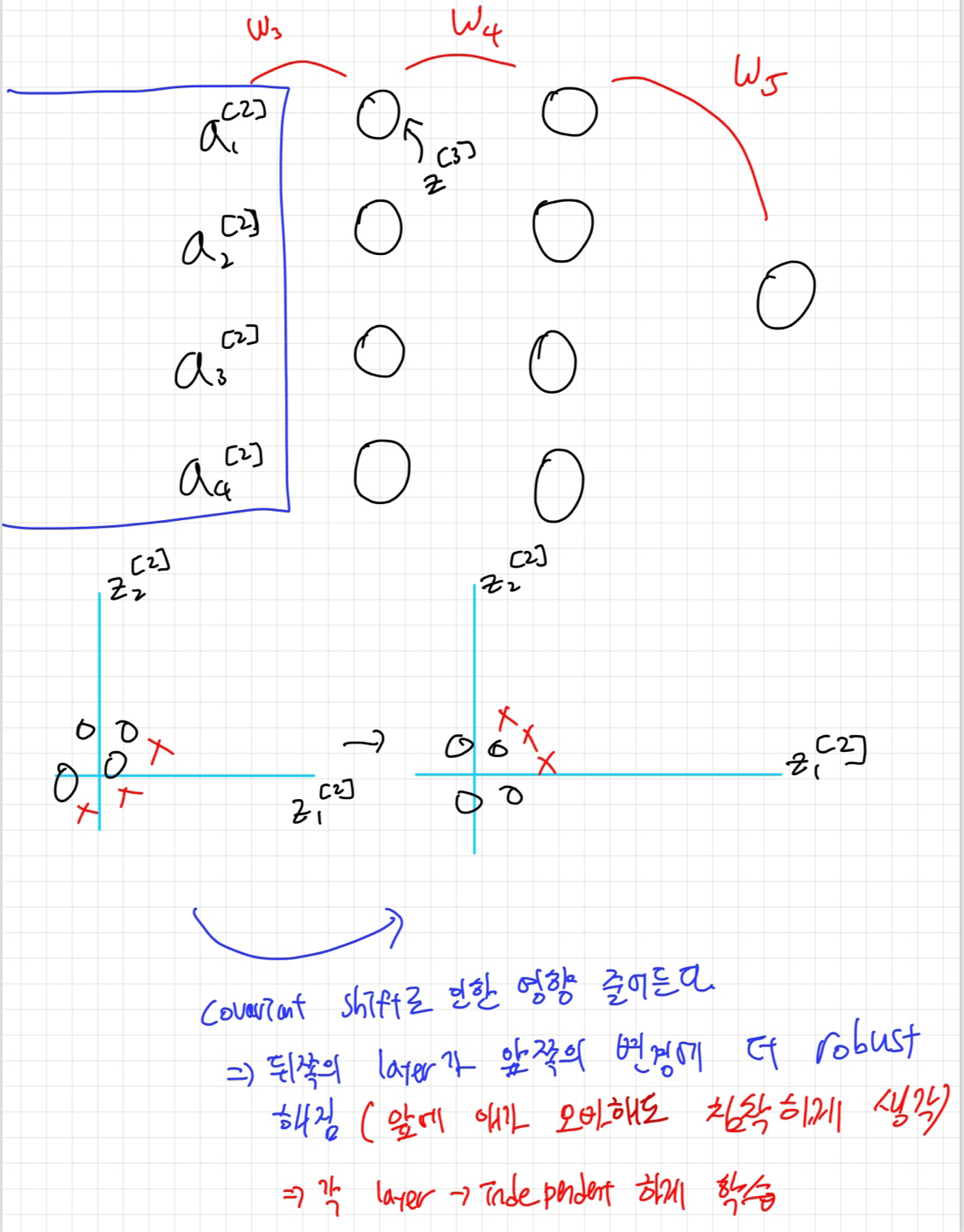
Batch Norm의 또 하나의 장점은 각 layer가 covariant shift에 대해서 robust해진다는 건데요 :)

Covariant shift는 머신러닝에서 모델을 학습시킬 때 사용하는 데이터의 분포와, 실제 모델을 적용할 때의 데이터 분포 사이에 차이가 발생하는 현상을 의미합니다. 간단히 말해, 학습 데이터와 테스트 데이터가 서로 다르게 분포되어 있을 때 이를 covariant shift라고 부릅니다. 이러한 차이가 모델의 성능을 저하시킬 수 있습니다.

검은 고양이로 학습을 시켰는데 다른색의 고양이들이 들어왔다고 개라고 출력하면 안되겠죠.

배치 정규화(Batch Normalization, BN)는 이 문제를 해결하는 데 도움이 되는 기술 중 하나입니다. 배치 정규화를 통해, 학습 과정에서 각 층의 입력 데이터가 일정한 분포를 유지하도록 하여, 코버리언트 시프트의 영향을 줄입니다 (정규화를 통해 색깔과 같은 다양한 조건에 덜 민감해집니다. 즉, 값을 낮춰 색깔이라는 특징을 예전만큼 중요하게 보지 않음). 결과적으로, 배치 정규화는 모델이 학습 데이터의 변화에 더 강건하게 만들고, 학습 속도를 향상시키며, 전반적인 모델의 성능을 개선하는 데 도움을 줍니다.

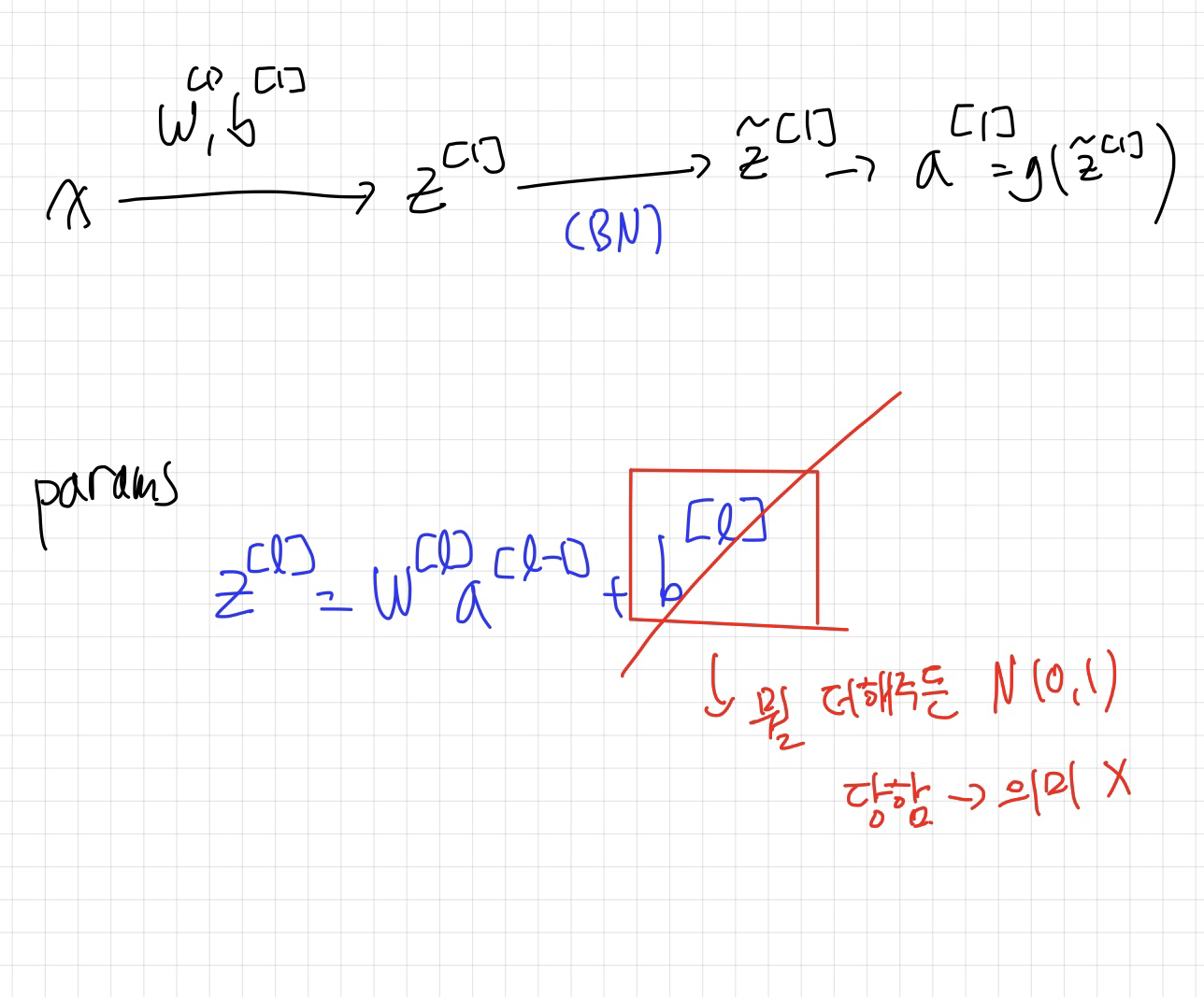
한가지 주의 할 점은 BN이 적용된 layer에서 bias값은 필요 없다는 것 입니다. 어차피 N(0,1)로 정규화되기 때문이죠 무슨값을 더해주던 간에.

test 때는 1번 배치때 산출한 평균, 2번 배치때 산출한 평균.... n번 배치 때 산출한 평균을 EWA해서 평균을 구하고 표준편차도 같은 방식으로 구한뒤 normalize한 후 감마를 곱하고 베타를 더해서 activation function 으로 전달합니다.

Hyperparameter tuning과 Batch Normalization에 대해서 알아보았는데요.
유익한 시간이였으면 합니다 :)