
안녕하세요, Optimization 두번째 파트입니다.😊
더 Advanced된 최적화 방법에 대해서 알아보기 전에 알고 가셔야 할 개념이 있습니다. 같이 한번 살펴보시죠!
Exponentially weighted average
Exponentially Weighted Moving Average (EWMA)는 딥러닝이나 기계 학습에 국한된 개념이 아닙니다. 원래 이 개념은 통계와 신호 처리 분야에서 오랫동안 사용되어 왔으며, 시계열 데이터의 추세를 부드럽게 추정하고 노이즈를 줄이는 데 효과적인 방법으로 알려져 있습니다.
산식은 아래와 같습니다.
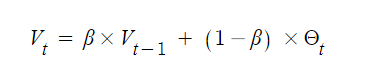
Vt는 현재 추정치 Vt-1는 이전시점에서의 추정치, Θt는 현재 시점 t에서의 실제 관측치, 그리고 β는 평활 계수(smoothing factor)를 나타냅니다.
β 값은 0과 1 사이에 있으며, 이 값에 따라 과거 관측치가 현재 추정치에 미치는 영향의 정도가 결정됩니다.
시간이 흐름에 따라 과거의 영향력(Vt-1)이 지수적으로 감쇠하도록 설계한 것 입니다.
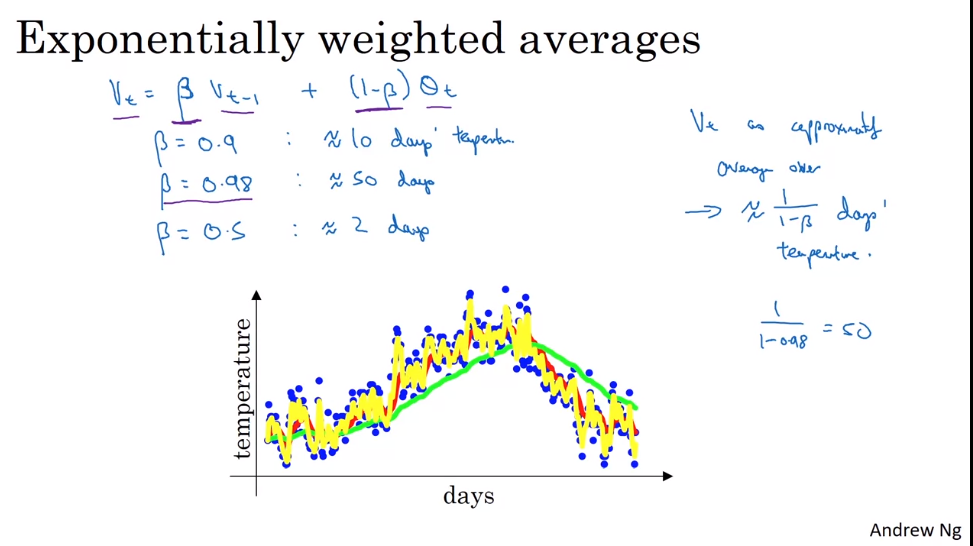
위의 그림은 날짜에 따라 런던의 온도를 추정하는 모델입니다.
수식에서 β 값이 0.9로 주어졌을 때, 이는 Vt가 대략적으로 최근 1⁄1-β 일 동안의 관측치의 평균을 나타낸다는 것을 의미합니다. 이경우 1⁄1-0.9의 값이 10이므로 Vt는 대략적으로 최근 10일 동안의 관측치의 평균을 나타냅니다.
딥러닝에서는 이전에 축적된 데이터의 영향을 지수적으로 감소시키면서 최신 데이터에 더 큰 가중치를 두는 EWA의 특성이 최적화 알고리즘을 설계할 때 매우 유용하게 활용됩니다. 특히, 경사 하강법의 변형인 모멘텀 최적화(momentum optimization) 및 Adam과 같은 고급 최적화 알고리즘에서 EWA는 경사의 변동성을 줄이고, 학습 과정을 안정화시키며, 더 빠른 수렴을 돕는 역할을 합니다.
β의 값이 클수록 EWA에서 과거 데이터가 현재 추정치에 더 큰 영향을 미칩니다. 이는 연속된 그라디언트 업데이트들 사이의 변동을 평활화(smooth out)함으로써 경사의 변동성을 줄이는 효과를 가집니다.
Memory 측면의 장점
지수 가중 이동 평균은 평균을 계산할 때 이전의 모든 값에 가중치를 부여하지만, 가중치는 시간이 지날수록 지수적으로 감소합니다. 이 방식은 메모리를 절약하는데, 모든 과거 값을 저장할 필요 없이 현재의 가중 평균값 하나만 유지하면 됩니다. 반면에, 단순 이동 평균(Simple Moving Average, SMA)을 계산하려면 최근 N일의 데이터를 모두 저장해야 합니다.
단순 이동 평균 (SMA)
- 10일간의 데이터를 모두 저장해야 합니다:
[T1, T2, T3, ..., T10] - 이 데이터를 사용하여 평균을 계산합니다:
SMA = (T1 + T2 + T3 + ... + T10) / 10 - 메모리 사용량은 10개의 온도값을 저장해야 하므로 10개 변수의 메모리가 필요합니다.
지수 가중 이동 평균 (EWA)
- 오직 가장 최근의 가중 평균
V만 저장합니다. - 새로운 온도값
T_new가 주어지면, 새로운 가중 평균을 다음과 같이 갱신합니다:V_new = β * V + (1 - β) * T_new - 여기서
β는 가중치 감소율 (예: 0.9) 입니다. - 메모리 사용량은 단지 하나의 가중 평균 값을 저장하면 되므로 1개 변수의 메모리만 필요합니다.
메모리 사용 예
각 온도값을 저장하는 데 8바이트의 메모리가 필요하다고 가정해 봅시다.
SMA의 경우:
- 10일치 데이터:
10일 * 8바이트/일 = 80바이트
EWA의 경우:
- 1개의 가중 평균 값:
1 * 8바이트 = 8바이트
SMA와 비교했을 때, EWA는 80바이트 대신 8바이트만 사용하므로 메모리 사용량을 90% 감소시킵니다. 이는 특히 대량의 데이터를 다루어야 할 때, 혹은 메모리에 제약이 있는 시스템에서 효율적입니다.
Bias correction
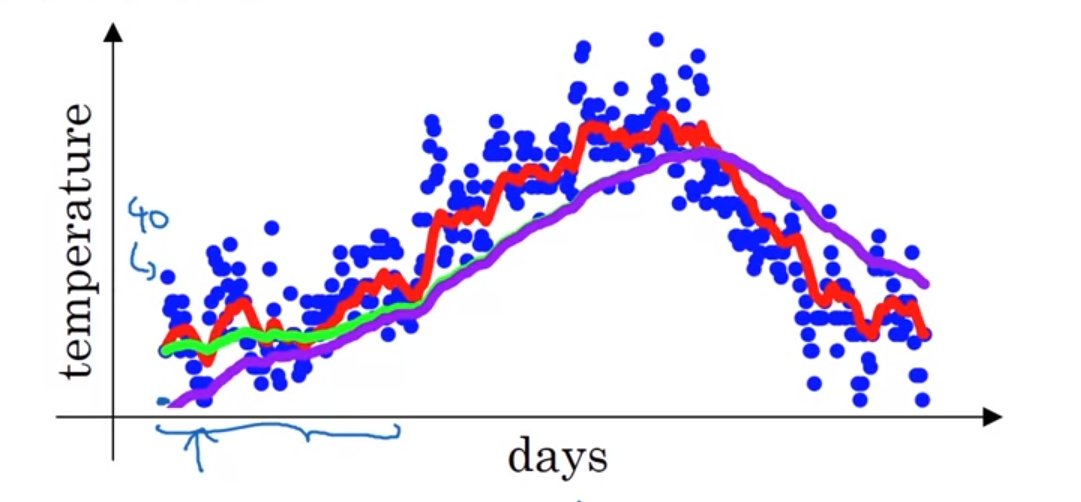
초기 추정 값의 문제
EWA를 0으로 초기화하고 계산을 시작할 때, 초기 값들은 실제 데이터보다 훨씬 낮게 추정되는 경향이 있습니다. 예를 들어, 첫 번째 날의 온도가 40도라면, 베타(β)가 0.98일 때 첫 번째 추정치 ( V_1 )은 0.8도로 계산되어 매우 낮은 값이 됩니다.
초기 추정치의 정확도를 높이기 위해, 각 추정치 ( V_t )를 ( 1 - β^t )로 나누는 편향 보정을 적용합니다. 여기서 ( t )는 현재 날짜(또는 시간 단계)입니다. 이는 초기 추정치가 실제 값에 더 가깝게 되도록 도와줍니다.
편향 보정의 장기적 영향
시간이 지남에 따라 ( β^t )는 0에 가까워지므로, 편향 보정은 시간이 지날수록 영향이 줄어듭니다. 즉, ( t )가 크면 편향 보정은 거의 차이를 만들지 않습니다.
기계 학습에서의 편향 보정 사용 여부
대부분의 기계 학습 구현에서는 초기의 편향된 추정치가 시간이 지남에 따라 빠르게 해소되므로 편향 보정을 종종 생략합니다. 하지만, 초기 단계의 정확도가 중요한 경우에는 편향 보정을 적용하여 더 정확한 초기 추정치를 얻을 수 있습니다.
이번 포스트에는 EWA에 대해서 알아보았는데요! 다음엔 이를 이용한 다양한 최적화 기법들에 대해서 알아보는 시간을 가져보도록 하겠습니다.
