우리는 종종 Loss함수를 minimize하는 과정이 MLE(Maximum likelihood estimation)와 연관있다는 이야기를 듣곤한다.
이것 역시 시간이 지나면 많이 까먹게 되는 개념인 것 같아 오늘은 MSE가 어떻게 MLE와 직접적으로 연결되는지 알아볼 것이다.
MLE(Maximum likelihood estimation)
먼저 아래의 확률 분포를 주목하자.
데이터 x값이 나와있고 그에 따른 distribution 그래프가 두개 나타나 있다.
데이터가 아래 그림과 같이 (1,4,5,6,9)로 주어졌으면 distribution이 주황색인 것과 파랑색인 것, 어떤게 더 합리적일까? 직관적으로 보면 당연히 주황색 확률 분포가 더 합리적이라고 느껴질 것이다.
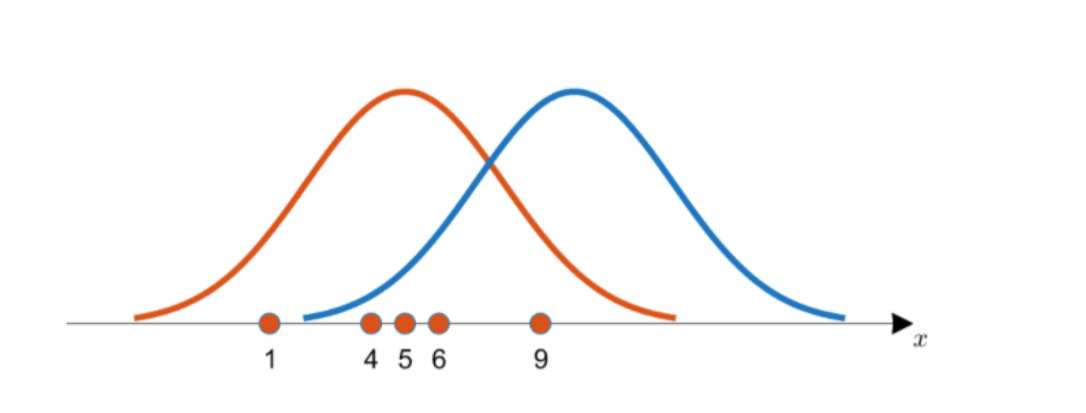
이는 주황색의 likelihood값이 더 크기 때문인데,여기서 likelihood란 이 각 데이터샘플들의 높이값들을 다 곱해준 값이라고 생각하면 된다. 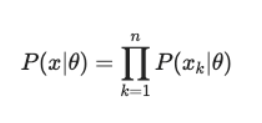
위의 식은 likelihood function, n개의 각 데이터샘플에 해당하는 확률밀도함수값을 곱해준 것이다.
확률분포마다 식이 전부 다르기 때문에 likelihood값을 계산하는 과정도 각기 다르다.
위의 그림은 가우시안분포를 가정했기 때문에 가우시안분포에서 likelihood를 구하는 과정을 봐보자.
가우시안 식이 다음과 같다는 건 고등학교 수학시간에 모두 배웠을 것이다. 여기서 m은 평균을 의미하고 σ는 표준편차를 의미한다.
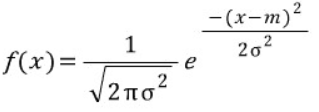
주황색 distribution의 평균을 5라고 가정하고 파랑색 distribution의 평균을 10이라고 가정하자(둘의 표준편차는 계산의 편의상 1로같다고 가정)
각각의 likelihood를 구해보면 아래와 같이 나타나고
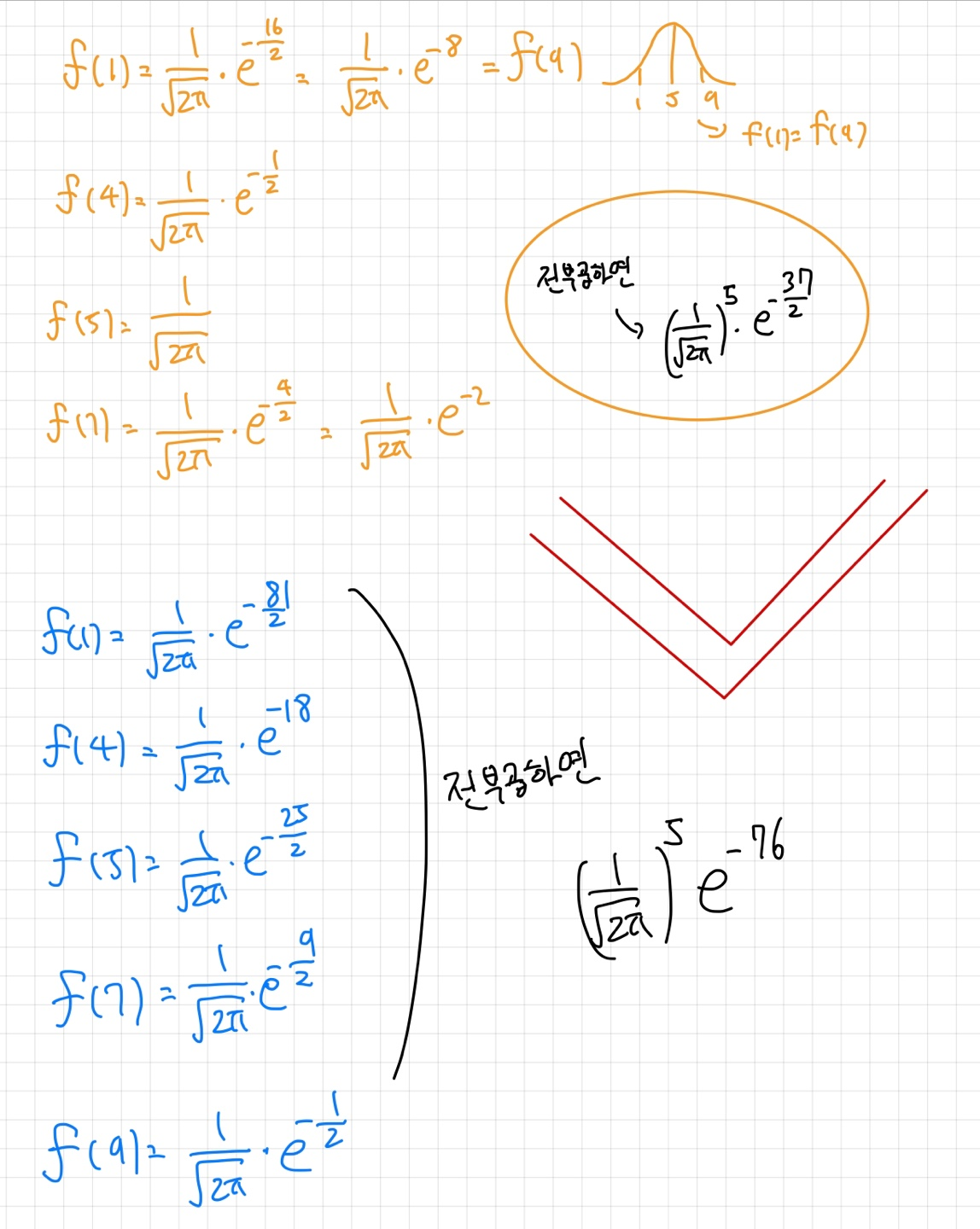
이는 우리가 관찰한 데이터에 대해 주황색 분포가 파란색 분포보다 더 큰 likelihood를 가진다고 직관적으로 판단한 것이 수학적으로도 일치함을 증명해준다
Maximum likelihood를 구하는 것은 이와 같이 여러 분포중에 가장 합리적인 분포를 찾는 것이라고 할 수 있다.
MSE
이제 이 개념을 MSE와 연결시켜볼건데, 가우시안 분포에 대한 MLE를 구하는 과정은 MSE를 최소화시키는 과정과 동일하다는 statement를 잘 기억해주시길 바란다.
우리는 평수(x)에 따라 집값(y)을 예측하는 linear regression task를 받았다. 우리의 목표는 알맞은 w,b값을 구하는 것.
y=wx+b로 놓았고 데이터셋은 총 5개 주어졌다고 해보자.
"y는 평균이 wx+b인 가우시안 분포를 따를 것이다"라고 가정을 하는 것.
우리에겐 아까와는 다르게 두개의 데이터값(x,y)이 주어졌다.
따라서 우리가 likelihood를 최대화 시키는 W,b를 구하는 것은 5개의 각각의 데이터 값에서 모두 합리적인 확률분포를 나타내게 하는 General한 W,b를 구하는 것 과 같다.
즉 이전처럼 평균이 고정된 가우시안 분포를 추정하는게 아니라 x에 따라서 평균이 계속 달라지지만 General하게 잘 동작하는 w,b를 잘 구해 냄으로써 그 어떤 데이터 셋에 대해서도 합리적인 확률분포를 구해낼 수 있는 것이다.
x의 값에 따라 변하는 평균을 갖는 가우시안 분포를 통해, 어떤 데이터셋에 대해서도 타당한 확률 분포를 예측할 수 있게 하는 것--> Likelihood 최대화
a를 최대화시키는 행위와 log a를 최대화시키는 행위는 같다.
y=x와 y=log x가 단조증가함수이기 때문
따라서 MLE를 구하는식은 아래와 같이 변환될 수 있고 이는 MSE를 minimize하는 과정과 동일하다는 것을 잘 나타낸다.

아래 예시는 각기 다른 w,b값이 어떻게 likelihood값을 변화시키는지를 나타낸다.
첫 번째 (x1,y1)=(1,2)에 대해서는 w=1,b=1일때와 w=3,b=-1일때의 확률분포가 같지만
두 번쨰 (x2,y2)=(2,3)에 대해서는 w=1,b=1일때와 w=3,b=-1일 때의 확률분포가 달라서 실제 y2값에 대한 확률밀도값이 크게 달라지는 것을 볼 수 있다.
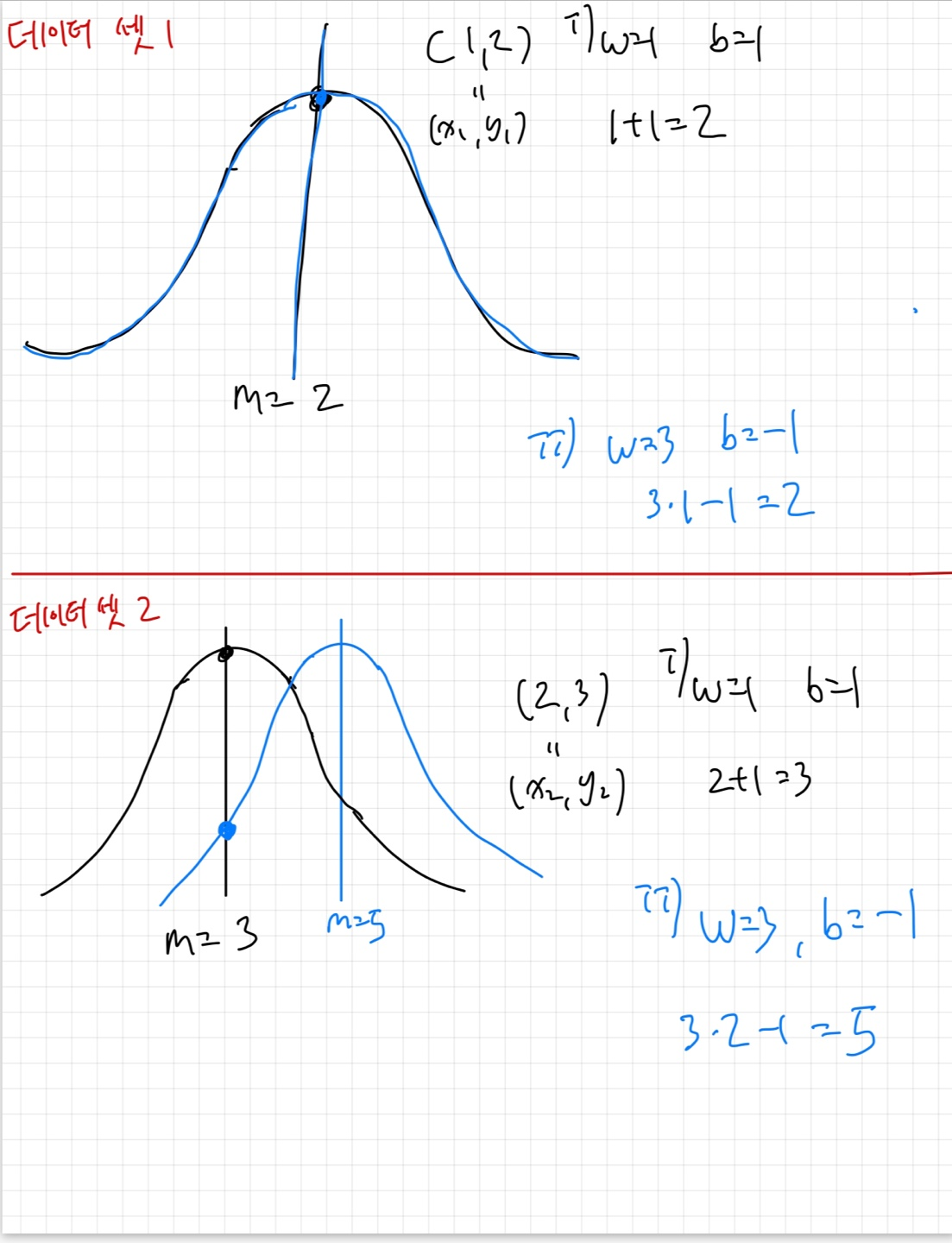
우리의 최종목표는 이러한 확률분포의 likelihood를 최대화하는 w,b를 구하는 것이고 이전의 case와 달리 데이터셋마다 확률분포가 달라진다는 점을 유의하자.
