
Weight를 학습하는 과정에서 우리는 종종 어떠한 경사하강법을 이용해야 할지 결정해야 할 순간들이 옵니다. 실제 모델을 구현할땐 그냥 adam(W)을 쓰긴하지만...강의를 듣다 개념들이 조금은 헷갈려서 정리해 보도록 하겠습니다.
대표적인 경사하강법 세 개에 대해서 짚고 넘어가 보도록 하죠.
Batch Gradient descent
데이터의 총 개수가 50개라고 가정해봅시다.
이 상황에서 배치 경사 하강법을 사용할 때는, 모든 데이터 포인트에 대한 기울기를 계산하고 그 평균값을 취합니다. 이 평균 기울기에 학습률(learning rate)을 곱한 값을 현재 가중치에서 차감함으로써, 모델을 최적화하는 방식으로 진행됩니다. iteration하나당 50개를 다 계산해야하기 때문에 시간이 비교적 오래걸린다는 단점이 있습니다.
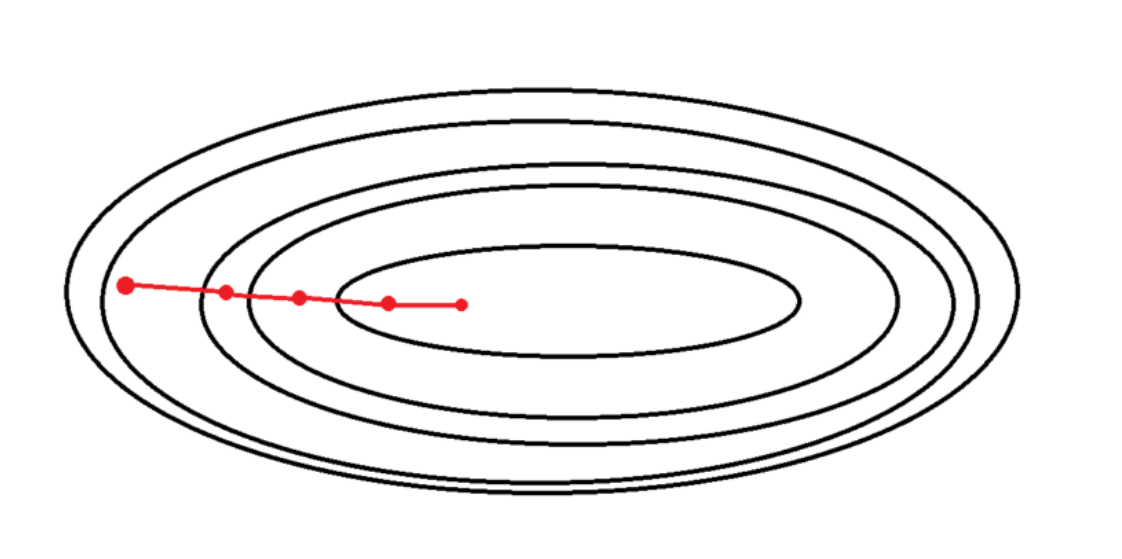
training data가 적을때(m<2000) batch GD를 많이 사용합니다.
시간이 오래 안걸리거든요.
Mini-batch Gradient descent
미니 배치 경사 하강법에서는 전체 데이터 세트를 사용하는 대신,
지정된 크기의 데이터 포인트를 선택하여 미니 배치를 형성합니다.
그런 다음 이 미니 배치에 대한 기울기의 평균을 계산하고, 이 평균에 학습률을 곱한 후, 결과값으로 가중치를 업데이트합니다.
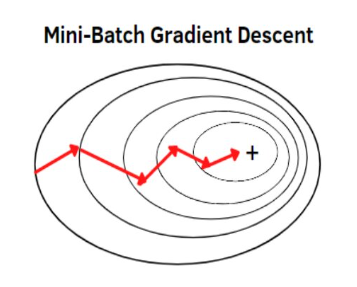
mini-batch size가 5라면, 다섯 개의 데이터 포인트를 하나의 미니배치로 간주하고, 각 데이터 포인트에 대한 기울기를 계산한 후 평균을 내어 가중치 업데이트를 한 번만 수행하는 것입니다.
mini-batch 사이즈는 저희가 지정해야하는 하이퍼파라미터입니다.
typical mini-batch size=64,128,256,512
CPU/GPU memory에 알맞은 mini-batch를 사용하라는 교수님의 첨언이 있었습니다.
Batch GD vs mini-batch GD
이 두가지 방법의 optimization 과정을 비교해봅시다.
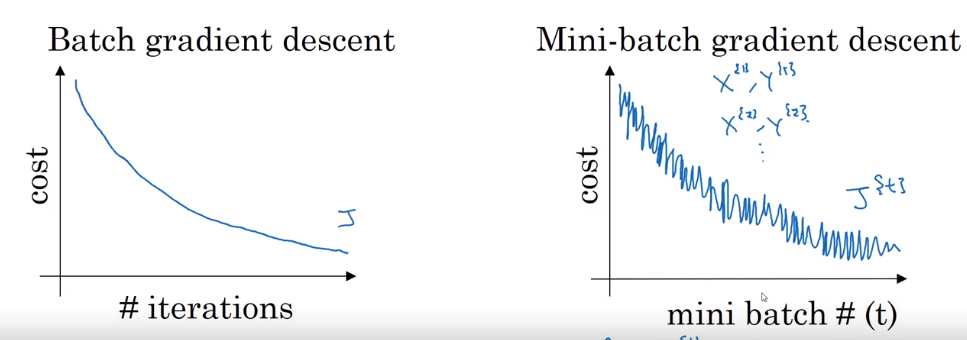
mini batch GD의 cost function그래프가 조금더 noisy 한 것을 확인할 수 있죠.
이는 mini batch GD의 batch사이즈가 더 작고, iteration을 거칠때마다 매번 다른 데이터셋을 학습하다보니 일반적인 특징을 반영하기 보다는,
매번 그때 그때의 mini-batch의 specific한 feature를 반영하기 때문에 그림이 다음과 같이 noise가 섞인 형태로 난다고 보시면 될 것 같습니다.
그래도 이를 여러번 반복하면 general하게 잘 학습이 되는 걸 볼 수 있죠.
그러나 이러한 노이즈는 꼭 부정적인 것만은 아닙니다.이러한 불규칙성은 모델이 local minima에 빠지는 것을 방지하고, 더 좋은 global minimum을 찾는 데 도움이 될 수 있습니다.😁
반면에 batch gradient descent는 같은 전체 데이터셋을 iteration마다 학습하기 때문에 좀 더 general한 feature들을 배운다는 것을 확인하실수 있습니다.
Traditional Stochastic Gradinet descent
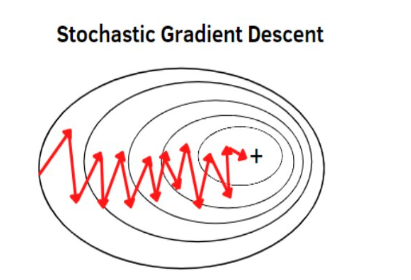
이 방법에서는 각 데이터 포인트마다 개별적으로 가중치를 업데이트합니다. 즉, 1번 데이터에 대해 기울기를 계산하고 가중치를 업데이트한 후, 2번 데이터에 대해 같은 과정을 반복한다. 이 경우, 각 데이터 포인트마다 업데이트가 일어나므로, 50개의 데이터 포인트가 있다면 가중치 업데이트도 50번 발생합니다.
Traditional SGD vs Mini-batch GD
-
잡음 감소: 앞서 언급했듯이 미니배치 경사 하강법은 각 배치에서 여러 데이터 포인트의 평균 기울기를 사용한다. 이렇게 하면 개별 데이터 포인트의 노이즈가 평균화되어 전체 기울기 계산이 더 안정적이 된다. 반면, 확률적 경사 하강법은 개별 데이터 포인트에 대한 기울기를 그대로 사용하기 때문에 노이즈의 영향을 더 많이 받는다.
ex) 1번 데이터의 노이즈가 10만큼 있었다면(굳이 수치화 하자면) mini-batch에서는 평균화 되어서 2만큼 가중치 업데이트에 영향을 주지만 SGD에서는 그대로 10만큼 영향을 주게된다.
-
더 효율적인 계산: 미니배치를 사용하면 데이터 처리를 벡터화하고 행렬 연산을 최적화하여 더 효율적으로 계산할 수 있다. 이는 특히 GPU와 같은 하드웨어 가속을 사용할 때 중요한 이점이 된다. 그러나 확률적 경사 하강법(SGD)에서는 벡터화를 통해 속도를 향상시키는 이점을 활용할 수 없습니다.
-
수렴 속도 및 안정성의 균형: 미니배치는 확률적 경사 하강법의 빠른 수렴 속도와 전체 배치 경사 하강법의 안정성 사이에서 균형을 맞춘다. 미니배치는 노이즈가 적어서 안정적이면서도, 개별 데이터 포인트보다 빠르게 수렴할 수 있다.
Batch gradient descent와 SGD의 장점들만 가져왔다고 생각하자
-
로컬 최소점(Local Minima) 및 안장점(Saddle Points) 탈출: 미니배치의 잡음 수준은 SGD보다 낮지만, 때때로 로컬 최소점이나 안장점에서 벗어나는 데 충분한 변동성을 제공한다. 이는 전체 배치보다 더 효과적일 수 있다.
각 샘플은 전체 데이터 분포를 완벽하게 대표하지 않기 때문에 SGD의 경우 기울기 추정에 비교적 높은 변동성을 초래한다. (예기치 않게 더 안장점을 넘어 더 낮은 지점으로 갈 수 있다.)
