기저벡터의 변경

기저벡터는 특정 공간을 정의할 수 있는 한 단위의 벡터들을 의미한다. 우리가 흔히 사용하는 표준 좌표계에서는 아래와 같은 기저벡터를 갖는다.

우리가 자주 사용하는 표준 좌표계를 선형변환하여 공간을 일그러뜨려도 각 축에서 기저벡터로 그 공간을 표현할 수 있다. 중요한 것은, 같은 벡터여도 기저벡터에 따라서 표현하는 방법이 달라진다는 것이다!

아래 이미지를 보면, 우리가 표현하고 싶은 벡터인 노란색 벡터는 변함이 없다. 하지만 기저벡터가 바뀜에 따라 이 벡터는 $\begin{bmatrix} 3 & 2 \end{bmatrix}^T$와 $\begin{bmatrix} \frac{5}{3} & \frac{1}{3} \end{bmatrix}^T$로 각각 달리 표현된다.

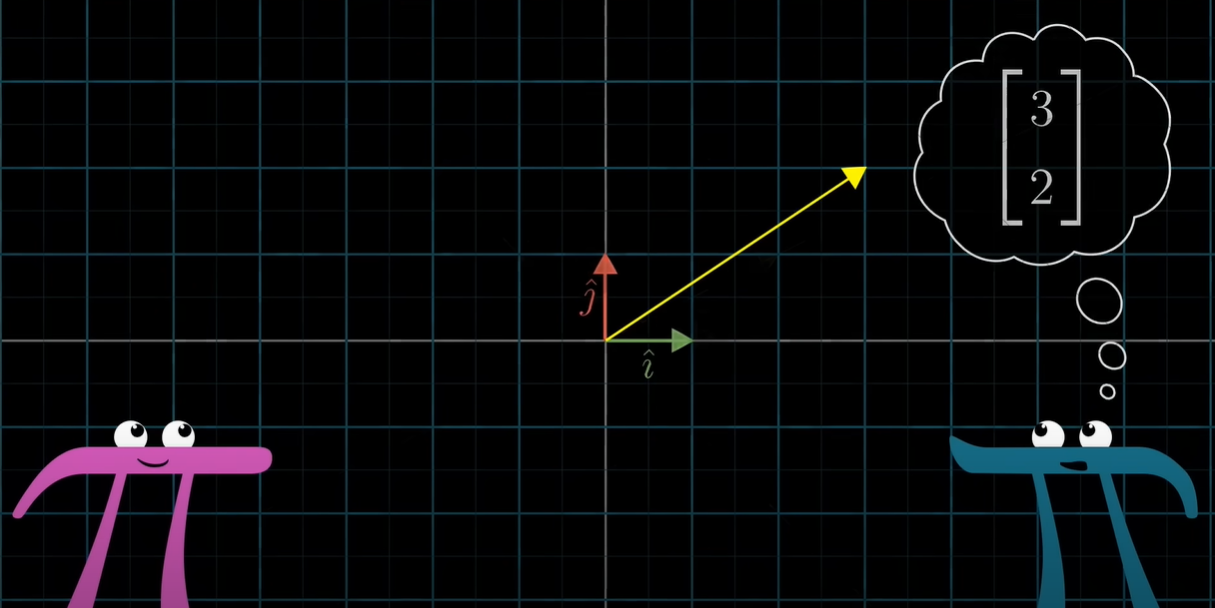
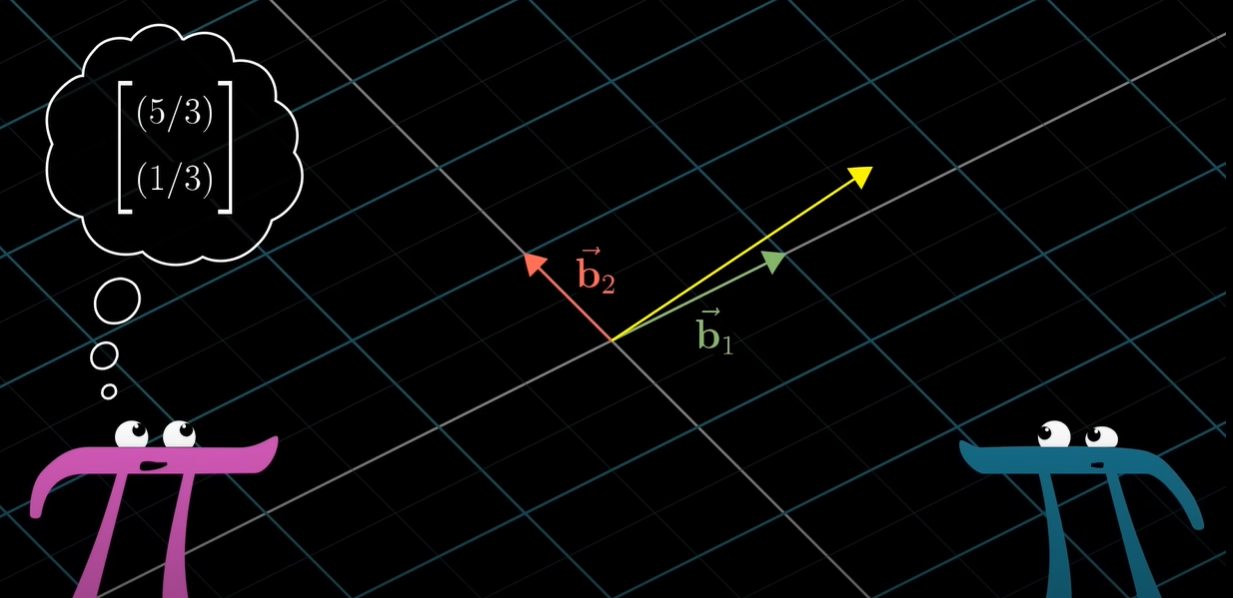
앞서 기저벡터는 그 공간을 표현할 수 있는 한 단위의 벡터라고 정의했다. 이 정의는 무슨 의미일까? 2차원 공간을 예로 들면, 언제나 기저벡터는 아래와 같다는 것이다.

조금 이상하다. 위에서 이미지로 든 예시에서 $\overrightarrow{b}_1, \overrightarrow{b}_2$만 하더라도 선형변환 결과가 $\begin{bmatrix} 1 & 0 \end{bmatrix}^T$, $\begin{bmatrix} 0 & 1 \end{bmatrix}^T$가 아닌데 말이다.

바뀐 기저벡터를 표준 좌표계에서 표현하면 $\begin{bmatrix} 1 & 0 \end{bmatrix}^T$, $\begin{bmatrix} 0 & 1 \end{bmatrix}^T$가 아니겠지만, 공간 자체가 변경 되었으므로 좌표계도 변경 되어야한다는 것이다! 바뀐 좌표계에서는 $\overrightarrow{b}_1, \overrightarrow{b}_2$가 $\begin{bmatrix} 1 & 0 \end{bmatrix}^T$, $\begin{bmatrix} 0 & 1 \end{bmatrix}^T$이라는 점이다.

좌표계가 바뀌면 그 안의 벡터들을 표현하는 방식이 달라지므로, 바뀐 공간 안에서의 벡터를 우리가 흔히 사용하는 표준 좌표계로 표현하는 방법을 알아야한다.

좌표계 변환

앞서 설명한 내용을 요약하자면, 서로 다른 좌표계에서는 같은 벡터를 보더라도 다르게 표현하기 때문에 좌표계를 변환하는 방법이 필요하다는 것이었다.

좌표계를 변환하는 방법은 무엇일까? 바로 행렬과 벡터의 곱이다.

위 식을 해석해보자. 표준 좌표계 입장에서 원본 벡터인 $\overrightarrow{v}$를 $A$라는 선형변환을 하여 $\overrightarrow{w}$가 된다는 것이다.

바뀐 좌표계 입장에서는 위 식은 아래와 같이 바뀐다.

역행렬은 선형변환 결과를 선형변환 이전으로 돌리는 행렬을 의미한다.(챕터 7 참고) 따라서 바뀐 벡터인 $\overrightarrow{w}$를 선형변환 전으로 롤백하는 $A^{-1}$를 거쳐 $\overrightarrow{v}$를 구할 수 있다.

행렬과 벡터의 곱은 생각보다 심오한 의미였던 것이다.