Moving Beyond Linearity

• Often the linearity assumption is good enough
  • When its not...
    • Polynomials
    • Step functions
    • Splines
    • Local regression
    • Generalized additive models
• Offer a lot of flexibility, without losing the ease and interpretability of linear models

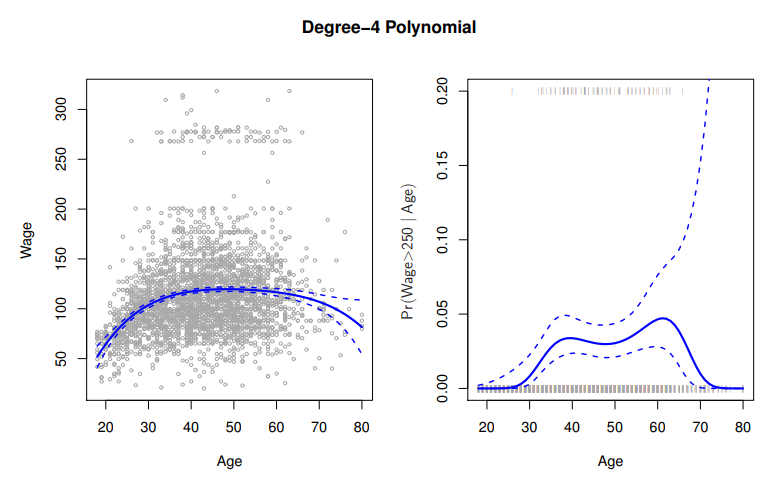
Details

• Create new variables $X_1=X, \;X_2=X^2$, etc and then treat as multiple linear regression
• Not really interested in the coefficients; more interested in the fitted function values at any value $x_0$
  $\hat f(x_0)=\hat\beta_0+\hat\beta_1x_0+\hat\beta_2x^2_0+\hat\beta_3x_0^3+\hat\beta_4x_0^4$
• Since $\hat f(x_0)$ is a linear function of the $\hat \beta_l$, can get a simple expression for pointwise-variances $\text{Var}[\hat f(x_0)]$ at any value $x_0$
• In the figure we have computed the fit and pointwise standard errors on a grid of values for $x_0$
• We show $\hat f(x_0) \pm 2 \times \text{se}[\hat f(x_0)]$
• We either fix the degree $d$ at some reasonably low value, else use cross-validation to choose $d$
• Logistic Regression follows naturally
  $\text{Pr}(y_i > 250|x_i) =\frac{\text{exp}(\beta_0+\beta_1x_i+\cdots+\beta_dx_i^d)}{1 + \text{exp}(\beta_0+\beta_1x_i+\cdots+\beta_dx_i^d)}$
  • To get confidence intervals, compute upper and lower bounds on the logit scale, and then invert to get on probability scale
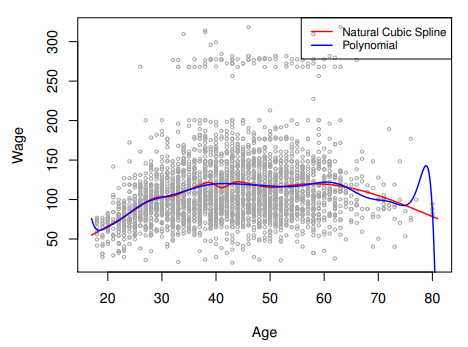
  • Polynomials have notorious tail behavior : very bad for extrapolation
• `Step Functions
  $C_1(X)=I(X<35),\;C_2(X)=I(35\leq X<50)\;C_3(X)=I(X\geq65)$
  
  • Useful way of creating interactions that are easy to interpret
  • Interaction effect of $Year$ and $Age$:
    $I(Year<2005)\times Age,\;I(Year\geq2005)\times Age$
    would allow for different linear functions in each age category
  • Choice of cutpoints or knots can be problematic
  • For creating nonlinearities, smoother alternatives such as splines are available

Picewise Polynomials

• Instead of a single polynomial in $X$ over its whole domain, we can rather use different polynomials in regions defined by knots
  $y_i = \begin{cases} \beta_{01} + \beta_{11} x_i + \beta_{21} x_i^2 + \beta_{31} x_i^3 + \epsilon_i & \text{if } x_i < c, \\ \beta_{02} + \beta_{12} x_i + \beta_{22} x_i^2 + \beta_{32} x_i^3 + \epsilon_i & \text{if } x_i \geq c. \end{cases}$
• Better to add contraints to the polynomials e.g. continuity
• Splines have the maximum amount of continuity
  

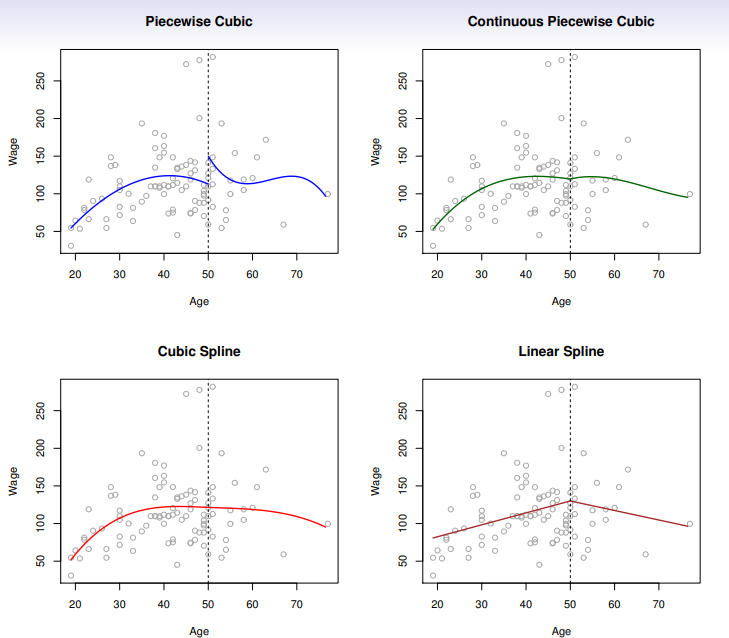
Linear Splines

• A linear spline with knots at $\xi_k$, $k=1,\dots,K$ is a piecewise linear polynomial continuous at each knot
• We can represent this model as
  $y_i = \beta_0 + \beta_1 b_1(x_i) + \beta_2 b_2(x_i) + \cdots + \beta_{K+1} b_{K+1}(x_i) + \epsilon_i,$
  where the $b_k$ are basis functions
  $b_1(x_i) = x_i \\ b_{k+1}(x_i) = (x_i - \xi_k)_+, \quad k = 1, \dots, K$
  Here the $()_+$ means positive part
  $(x_i - \xi_k)_+ = \begin{cases} x_i - \xi_k & \text{if } x_i > \xi_k, \\ 0 & \text{otherwise}. \end{cases}$
  

Cubic Splines

• A cubic spline with knots at $\xi_k$, $k=1, \dots, K$ is a piecewise cubic polynomial with continuous derivatives up to order $2$ at each knot
• Again we can represent this model with truncated power basis functions
  $y_i = \beta_0 + \beta_1 b_1(x_i) + \beta_2 b_2(x_i) + \cdots + \beta_{K+3} b_{K+3}(x_i) + \epsilon_i, \\ b_1(x_i) = x_i \\ b_2(x_i) = x_i^2 \\ b_3(x_i) = x_i^3 \\ b_{k+3}(x_i) = (x_i - \xi_k)^3_+, \quad k = 1, \dots, K$
  where
  $(x_i - \xi_k)^3_+ = \begin{cases} (x_i - \xi_k)^3 & \text{if } x_i > \xi_k, \\ 0 & \text{otherwise}. \end{cases}$
  

Natural Cubic Splines

• A natural cubic spline extrapolates linearly beyond the boundary knots
• This adds $4=2\times 2$ extra contraints, and allows us to put more internal knots for the same degrees of freedom as a regular cubic spline
  
  

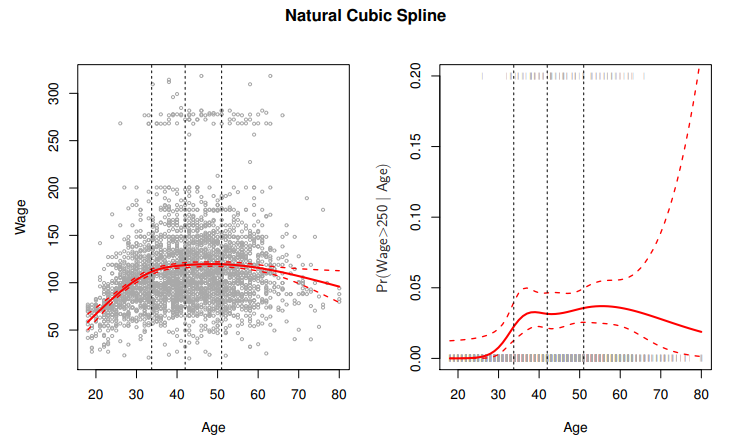
Knot Placement

• One strategy is to decide $K$, the number of knots, and then place them at appropriate quantiles of the observed $X$
• A cubic spline with $K$ knots has $K+4$ parameters or degrees of freedom
• A natural spline with $K$ knots has $K$ degrees of freedom
  

Smoothing Splines

• Consider this criterion for fitting a smooth function $g(x)$ to some data:
  $\text{minimize}_{g \in S} \sum_{i=1}^{n} \left( y_i - g(x_i) \right)^2 + \lambda \int \left( g''(t) \right)^2 dt$
• The first term is RSS, and tries to make $g(x)$ match the data at each $x_i$
• The second term is a roughness penalty and controls how wiggly $g(x)$ is
• It is modulated by the tuning parameter $\lambda \geq 0$
  • The smaller $\lambda$, the more wiggly the function
  • Eventually interpolating $y_i$ when $\lambda = 0$
  • As $\lambda \rightarrow \infty$, the function $g(x)$ becomes linear

Some issues

• Smoothing splines avoid the knot-selection issue, leaving a single $\lambda$ to be chosen
• The vector of $n$ fitted values can be written as $\hat g_\lambda = S_\lambda y$, where $S_\lambda$ is a $n\times n$ matrix
• The effective degrees of freedom are given by
  $df_{\lambda} = \sum_{i=1}^{n} \{S_{\lambda}\}_{ii}.$

Choosing lambda

• The leave-one-out(LOO) cross-validation error is given by
  $RSS_{cv}(\lambda) = \sum_{i=1}^{n} \left( y_i - \hat{g}_{\lambd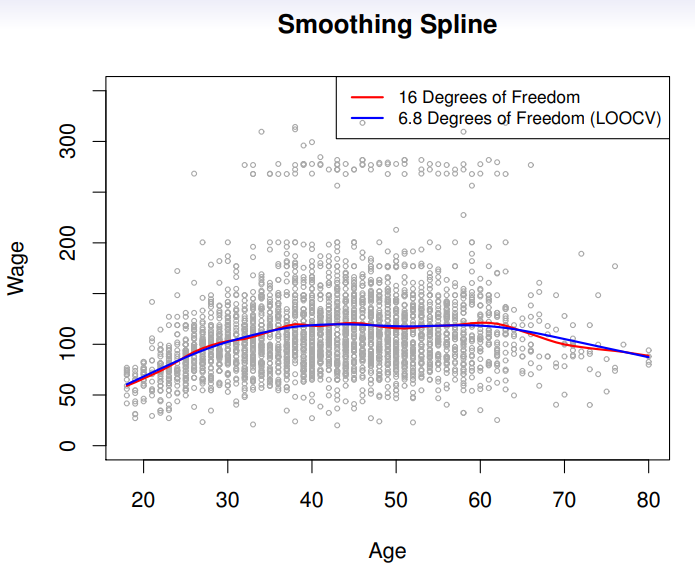a}^{(-i)}(x_i) \right)^2 = \sum_{i=1}^{n} \left[ \frac{y_i - \hat{g}_{\lambda}(x_i)}{1 - \{S_{\lambda}\}_{ii}} \right]^2.$
  

Local Regression

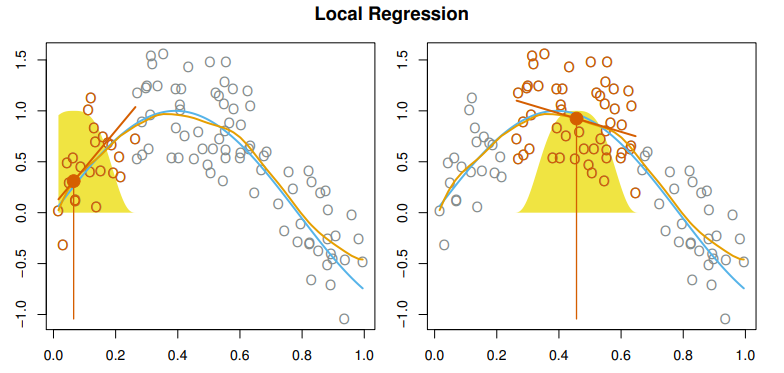
• With a sliding weight function, we fit seperate linear fits over the range of $X$ by weighted least squares

Generalized Additive Models

• Allows for flexible nonlinearities in several variables, but retains the additive structure of linear models

  $y_i = \beta_0 + f_1(x_{i1}) + f_2(x_{i2}) + \cdots + f_p(x_{ip}) + \epsilon_i.$

  

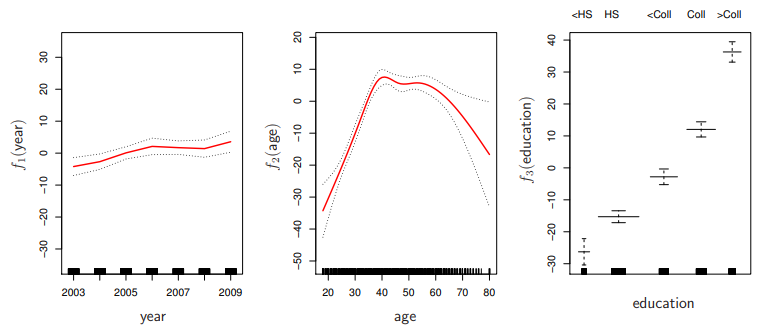
• Can fit a GAM simply using, e.g. natural splines

lm(wage~ns(year,df=5) +ns(age, df = 5) + education)

• Coefficients not that interesting; fitted functions are
• Can mix terms - some linear, some nonlinear - and use anove() to compare models

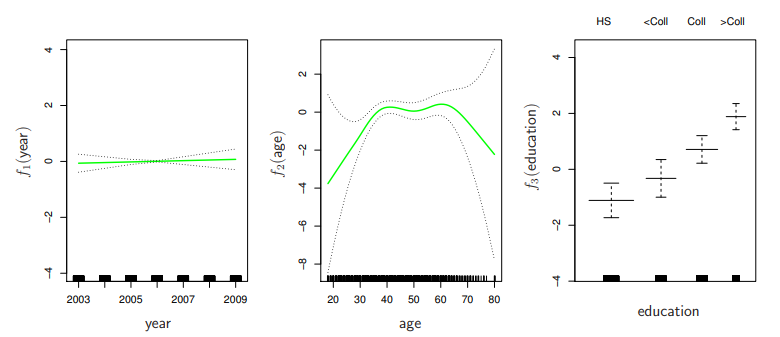
GAMs for Classification

All Contents written based on GIST - Machine Learning & Deep Learning Lesson(Instructor : Prof. sun-dong. Kim)