Cross-validation and the Bootstrap

• In the section we discuss two resampling methods
  • Cross-validation
  • Bootstrap
• These methods refit a model of interest to samples formed from the training set, in order to obtain additional information about the fitted model

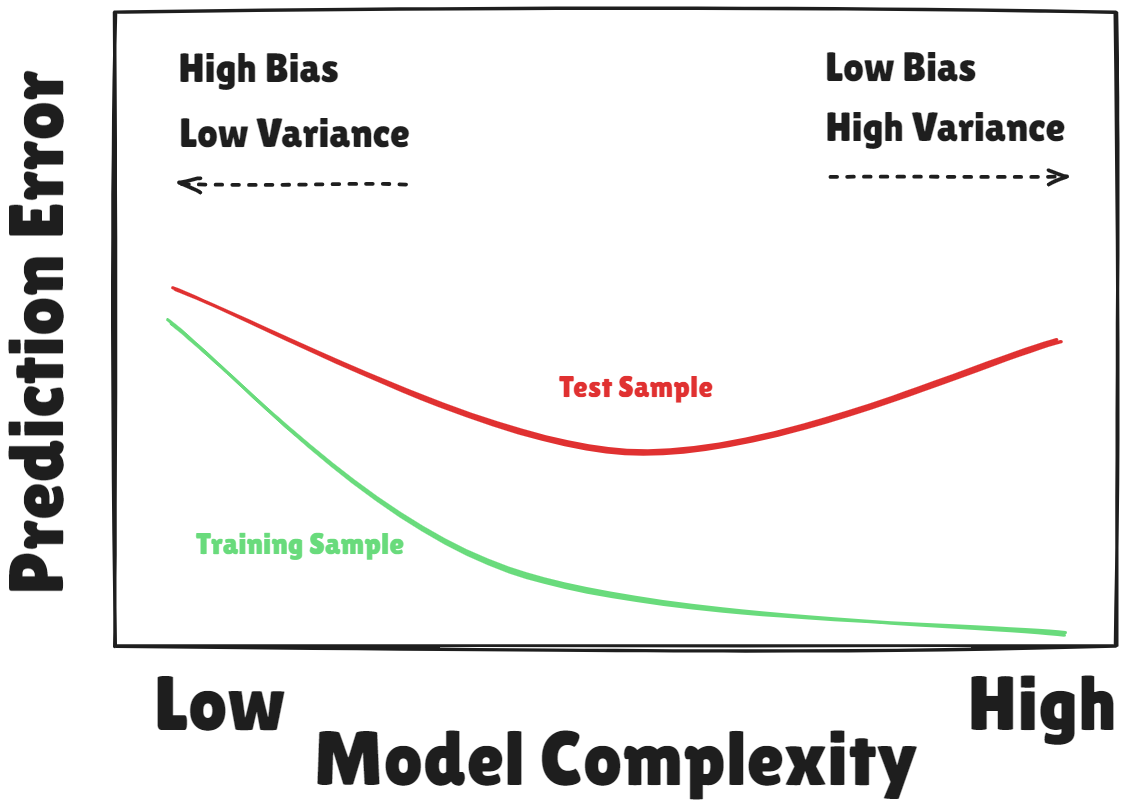
Training Error versus Test Error

• Recall the distinction between the test error and the training error
• test error is the average error that results from using a statistical learning method to predict the response on a new observation, one that was not used in training the method
• training error can be easily calculated by applying the statistical learning method to the observations used in its training

  But the training error rate often is quite different from the test error rate, and in particular the former can dramatically understimate the latter
  

More on prediction-error estimates

• Best solution : a large designated test set. Often not available
• Some methods make a mathematical adjustment to the training error rate in order to estimate the test error rate
  (These include the Cp statistic, AIC and BIC)
• Here we instead consider a class of methods that estimate the test error by holding out a subset of the training observations from the fitting process, and then applying the statistical learning method to those held out observations

Validation-set approach

• Here we randomly divide the available set of samples into two parts
  • training set
  • validation or hold-out set
• The model is fit on the training set, and the fitted model is used to predict the responses for the observations in the validation set
• The resulting validation-set error provides an estimate of the test error
• This is typically assessed using MSE in the case of a quantitative response and misclassification rate in the case of a qualitative (discrete) response
  
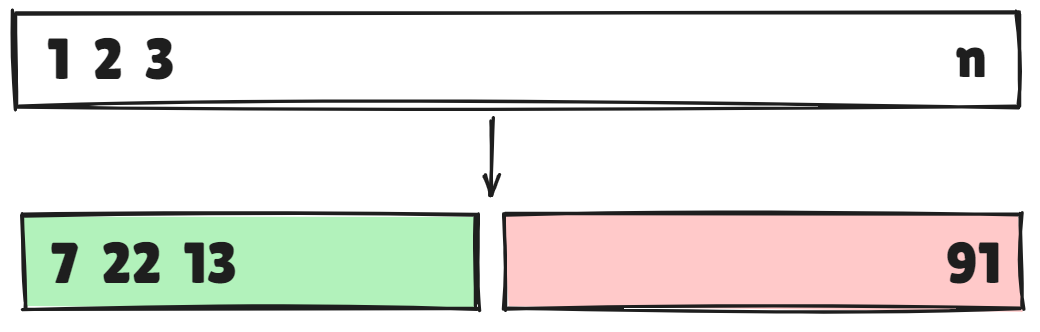
• A random splitting into two halves : left part is training set, right part is validation set
• The validation estimate of the test error can be highly variable, depending on precisely which observations are included in the training set and which observations are included in the validation set
• This suggests that the validation set error may tend to overestimate the test error for the model fit on the entire data set.

K-fold Cross-validation

• Widly used approach for estimating test error
• Estimates can be used to select best model, and to give an idea of the test error of the final chosen model
  • Idea is to randomly divide the data into $K$ equal-sized parts
  • We leave out part $k$, fit the model to the other $K-1$ parts (combined)
  • Obtain predictions for the left-out $k$th part
  • This is done in turn for each part $k=1,2,\dots ,K$, and then the results are combined
    
  • Divide data into $K$ roughly equal-sized parts $(K=5 \;\text{here})$
• Let the $K$ parts be $C_1,C_2,\dots ,C_K$, where $C_k$ denotes the indices of the observations in part $k$
• There are $n_k$ observations in part $k$ : if $N$ is a multiple of $K$, then $n_k =n/K$
• Compute
  $CV_{(K)}=\displaystyle\sum_{k=1}^K\frac{n_k}{n}\text{MSE}_k$
  where $\text{MSE}_k =\sum_{i \in C_k}(y_i -\hat y_i)^2 /n_k$, and $\hat y_i$ is the fit for observation $i$, obtained from the data with part $k$ removed
• Setting $K=n$ yields $n$-fold or leave-one out cross-validation(LOOCV)
• With least-squares linear or polynomial regression, an amazing shorcut makes the cost of LOOCV the same as that of a single model fit! The following formula hods:
  $CV_{(n)}=\frac{1}{n}\displaystyle\sum_{i=1}^n\left(\frac{y_i-\hat y_i}{1 -h_i}\right)^2$
  where $\hat y_i$ is the $i$th fitted value from the original least squares fit, and $h_i$ is the leverage(diagonal of the "hat" matrix)
• LOOCV sometimes useful, but typically doesn't shake up the data enough
• The estimates from each fold are highly correlated and hence their average can have high variance
• a better choice is $K=5$ or $10$

Other issues with Cross-validation

• Since each training set is only $(K-1)/K$ as big as the original training set, the estimates of prediction error will typically be biased upward why...?
• This bias is minimized when $K=n (LOOCV)$, but this estimate has high variance
• $K=5$ or $10$ provides a good compromise for this bias-variance tradeoff

Cross-Validation for Classification Problems

• We divide the data into $K$ roughly equal-sized parts $C_1, C_2, \dots ,C_k$
• $C_k$ denotes the indices of the observations in part $k$
• There are $n_k$ observations in part $k$: if $n$ is a multiple of $K$, then $n_k =n/K$
• Compute
  $CV_K=\displaystyle\sum_{k=1}^K\frac{n_k}{n}\text{Err}_k$
  where $\text{Err}_k =\sum_{i\in C_k}I(y_i\neq \hat y_i)/n_k$
• The estimated standard deviation of $CV_k$ is
  $\hat{\text{SE}}(\text{CV}_K) = \sqrt{\frac{1}{K} \sum_{k=1}^{K} \frac{(\text{Err}_k - \overline{\text{Err}}_k)^2}{K - 1}}$
• This is a useful estimate, but strictly speaking, not quite valid why...?

Cross-validation: right and wrong

• Consider a simple classifier applied to some two-class data:
  • Starting with 5000 predictors and 50 samples, find the 100 predictors having the largest correlation with the class labels
  • We then apply a classifier such as logistic regression, using only these 100 predictors
• How do we estimate the test set performance of this classifier?
• Can we apply cross-validation in step 2, forgetting about step 1?

No!

• This would ignore the fact that in Step 1, the procedure has already seen the labels of the training data, and made use of them
• This is a form of training and must be included in the validation process
• It is easy to simulate realistic data with the class labels independent of the outcome, so that true test error $= 50\%$, but the CV error estimate that ignores Step 1 is zero!
• We have seen this error made in many high profile genomics papers

The Wrong and Right Way

• Wrong : Apply cross-validation in step 2
• Right : Apply cross-validation in steps 1 and 2

The Bootstrap

• The bootstrap is a flexible and powerful statistical tool that can be used to quantify the uncertainty associated with a given estimator or statistical learning method
• For example, it can provide an estimate of the standard error of a coefficient, or a confidence interval for that coefficient

Bootstrap example

• Suppose that we wish to invest a fixed sum of money in two financial assets that yield returns of $X$ and $Y$, respectively, where $X$ and $Y$ are random quantities
• We will invest a fraction $\alpha$ of our money in $X$, and will invest the remaining $1-\alpha$ in $Y$
• We wish to choose $\alpha$ to minimize the total risk, or variance, of our investment
• In other words, we want to minimize $\text{Var}(\alpha X + (1-\alpha)Y)$
• One can show that the value that minimizes the risk given by
  $\alpha = \frac{\sigma^2_Y-\sigma_{XY}}{\sigma^2_X+\sigma^2_Y-2\sigma_{XY}}$
  where $\sigma^2_X=\text{Var}(X),\;\sigma^2_Y=\text{Var}(Y),\;\text{and}\;\sigma_{XY}=\text{Cov}(X,Y)$
• But the values of $\sigma^2_X, \sigma^2_Y$, and $\sigma_{XY}$ are unknown
• We can compute estimates for these quantities $\hat\sigma^2_x, \hat\sigma^2_Y,\;\text{and}\;\hat\sigma_{XY}$, using a data set that contains measurements for $X$ and $Y$
• We can then estimate the value of $\alpha$ that minimizes the variance of our investment using
  $\hat\alpha = \frac{\hat\sigma^2_Y-\hat\sigma_{XY}}{\hat\sigma^2_X+\hat\sigma^2_Y-2\hat\sigma_{XY}}$
• To estimate the standard deviation of $\hat \alpha$, we repeated the process of simulating 100 paired observations of $X$ and $Y$, and estimating $\alpha$ 1,000 times
• We thereby obtained 1,000 estimates for $\hat\alpha$, which we can call $\hat\alpha_1,\hat\alpha_2,\dots,\hat\alpha_{1000}$
• So roughly speaking, for a random sample from the population, we would expect $\hat\alpha$ to differ from $\alpha$ by approximately 0.08, on average
  

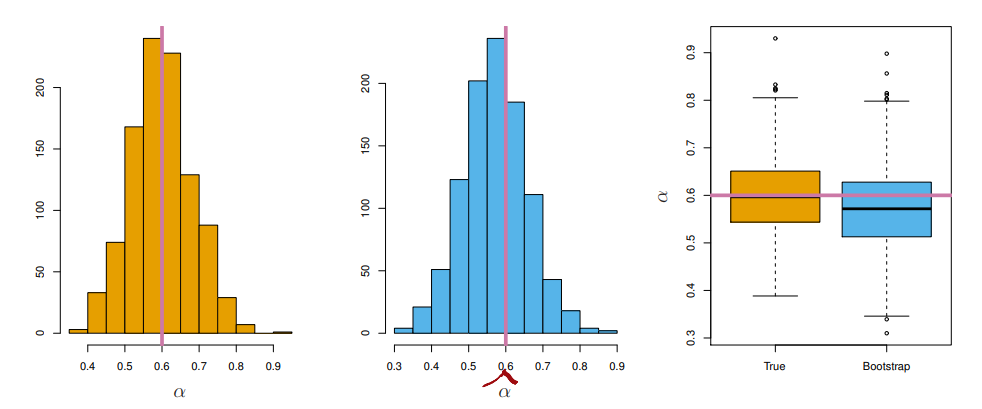
Real world Bootstrap

• The procedure outlined above cannot be applied, because for real data we cannot generate new samples from the original population
• However, the bootstrap approach allows us to use a computer to mimic the process of obtaining new data sets, so that we can estimate the variabillity of our estimate without generating additional samples
• Rather than repeatedly obtaining independent data sets from the population, we instead obtain distinct data sets by repeatedly sampling observations from the original data set with replacement
  
• In more complex data situations, figuring out the appropriate way to generate bootstrap samples can require some thought
• For example, if the data is a time seires, we can't simply sample the observations with replacement
• We can instead create blocks of consecutive observations, and sample those with replacements
• Then we paste together sampled blocks to obtain a bootstrap dataset

Can the bootstrap estimate prediction error?

• In cross-validation, each of the $K$ validation folds is distinct from the other $K-1$ folds used for training

  There is no overlap

• To estimate prediction error using the bootstrap, we could think about using each bootstrap dataset as our training sample, and the original sample as our validation sample
• But each bootstrap sample has significant overlap with the original data
• About two-thirds of the original data points appear in each bootstrap sample

  This will cause the bootstrap to seriously underestimate the true prediction error

• The other way around with original sample = training sample, bootstrap dataset = validation sample is worse

  Can partly fix this problem by only using predictions for those observations that did not (by chance) occur in the current bootstrap sample

• But the method gets complicated, and in the end, cross-validation provides a simpler, more attractive approach for estimating prediction error

Pre-validation

• Pre-validation can be used to make a fairer comparison between the two sets of predictors
• Divide the cases up into $K=13$ equal-sized parts of 6 cases each
• Set aside one of parts. Using only the data from the other 12 parts, select the features having absolute correlation at least
• 3 with the class labels, and form a nearest centroid classification rule
• Use the rule to predict the class lables for the 13th part
• Do steps 2 and 3 for each of the 13 parts, yielding a "pre-validated" microarray predictor $\hat z_i$ for each of the 78 cases
• Fit a logistic regression model to the pre-validated microarray predictor and the 6 clinical predictors

The Bootstrap versus Permutation tests

• The bootstrap samples from the estimated population, and uses the results to estimate standard errors and confidence intervals
• Permutation methods sample from an estimated null distribution for the data, and use this to estimate p-values and False Discovery Rates for hypothesis tests
• The bootstrap can be used to test a null hypothesis in simple situations
• Can also adapt the bootstrap to sample from a null distribution but there's no real advantage over permutations
  a

All Contents written based on GIST - Machine Learning & Deep Learning Lesson(Instructor : Prof. sun-dong. Kim)