1. Evaluation Metrics for Classification
1.1 Confusion matrix(혼동 행렬)
TP, TN, FP, FN으로 이루어진 매트릭스
분류모델의 성능 평가지표
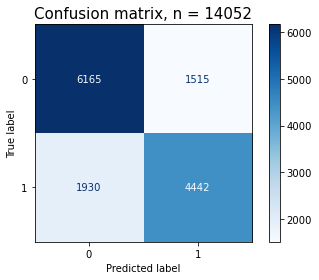
1.1.1 TP(True Positive)
실제 양성인데 검사 결과도 양성
잘 맞춰서, Positive(1)를 잡아냈다.
올바르게 1을 1이라고 예측. 찐양성, 찐양성
1.1.2 TN(True Negative)
실제 음성인데 검사 결과도 음성
잘 맞춰서 Negative(0)를 잡아냈다.
1.1.3 FP
실제 음성인데 검사 결과가 양성
잘 못해서 Positive라고 예측 → 원래는 Negative(0)인 것을 Positive(1)로 예측
1.1.4 FN
잘 못해서 Negative라고 예측 → 원래는 Positive(1)인데 Negative(0)로 예측
1.1.5 혼동 행렬의 사례
1.1.5.1 암 검진
암 검진에서 주로 봐야 할 지표는? False Negative!!
암 검진이 양성(1) → 암에 걸린 것
암 검진이 음성(0) → 암이 아닌 것
→ 암에 걸렸는데(Positive, 1) 암이 아니라고(Negative, 0) 오진하면 문제!!
1.1.5.2 스팸 분류
스팸 분류에서 주로 봐야 할 지표는? False Positive!!
스팸이면 1, 스팸이 아니면 0으로 분류
→ 원래는 스팸이 아닌데 스팸으로 분류
1.2 정밀도와 재현율, 임계값, F1_score
1.2.1 Accuracy(정확도)만으로 평가하면 안 되나요?

데이터 불균형이 있으면 정확도를 신뢰할 수 없다. 그 범주로만 찍어도 적당한 정확도가 나오니까...
→ 학습 데이터가 주로 0으로만 구성 → 0을 잘 맞추는 모델
진짜 문제를 해결하기 위한 예측이 잘 되었는 지를 볼 수 있는 지표가 필요!
1.2.2 정밀도와 재현율, 임계값
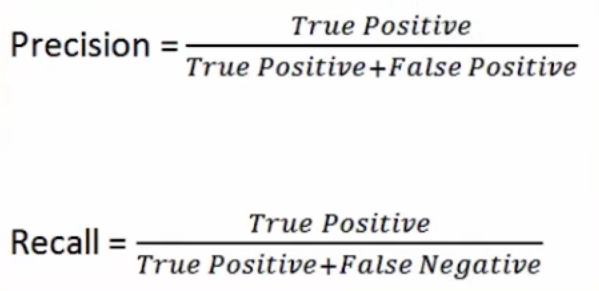
분모(FP, FN)가 커지면 문제가 커짐. 점수는 그만큼 낮게 나옴
1.2.2.1 정밀도(Precision)
1로 예측한 경우 중 모델이 1을 잘 맞춘 것의 비율
스팸 분류를 다룰 때 정밀도를 살펴봄!
1.2.2.2 재현율(Recall)
진짜 1인 것들 중 모델이 1로 맞춘 것의 비율
암 검진을 할 때 재현율을 살펴 본다.
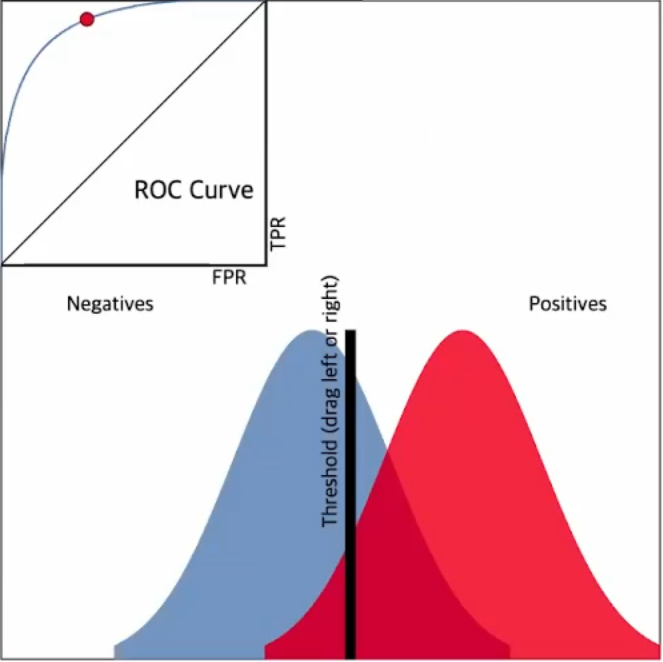
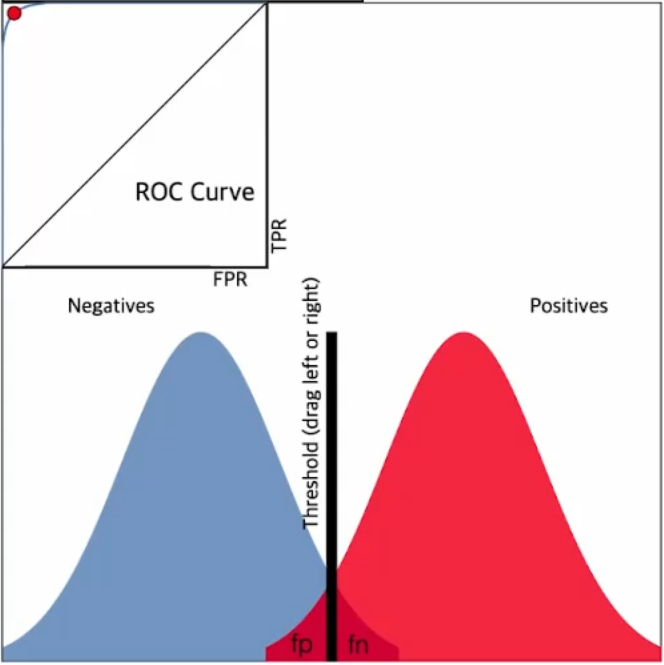
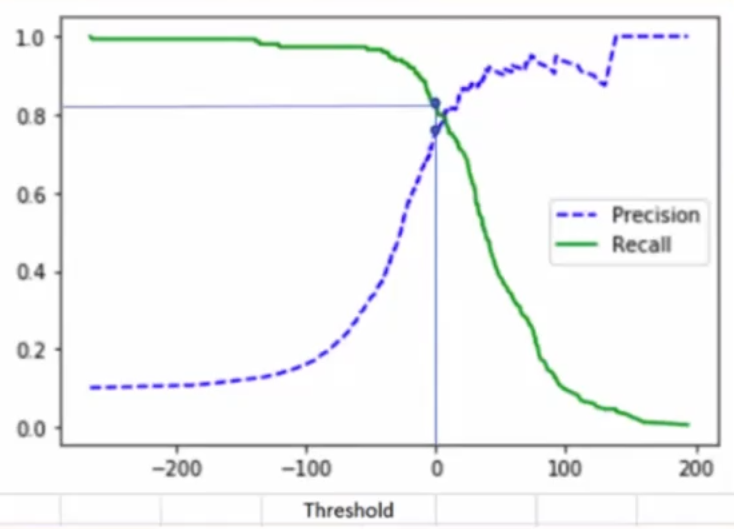
1.2.2.3 임계값(Threshold)
임계값을 낮추면? → 정밀도(Precision)가 낮아진다. 재현율(Recall)이 증가한다.
임계값을 높이면? → 정밀도(Precision)가 증가한다. 재현율(Recall)이 감소한다.
정밀도(Precision)와 재현율(Recall)은 트레이드오프 관계
1.2.2.4 F1_score(조화 평균)
정밀도(Precision)와 재현율(Recall)의 조화 평균
베타가 1이라는 말의 뜻? → 정밀도(Precision)와 재현율(Recall)의 가중치가 같다.
베타 > 1 → Recall에 가중치를 둔다.
베타 < 1 → Precision에 가중치를 둔다.
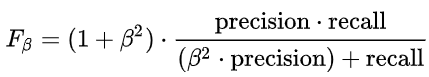
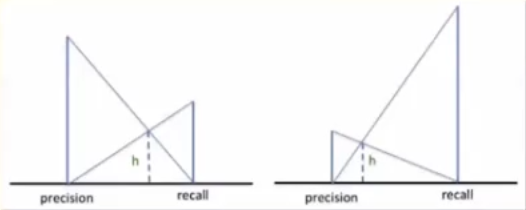
1.2.2.5 Accuracy(정확도)는 높아지는데, F1은 낮아진다. 무엇을 우선하여 보아야 하는가?
1.3 ROC curve, AUC
1.3.1 ROC curve란?
ROC = Receiver Operating Characteristic
AUC(=Area Under the Curve)는 ROC curve의 아래 면적을 의미함.
ROC curve, AUC를 사용하면 분류문제에서 여러 임계값 설정에 대한 모델의 성능을 구할 수 있음.
ROC curve는 여러 임계값에 대해 TPR(True Positive Rate, recall)과 FPR(False Positive Rate) 그래프를 보여줌.
임계값에 따른 재현율(Recall, TPR)과 위양성률(FPR, Fall-out)
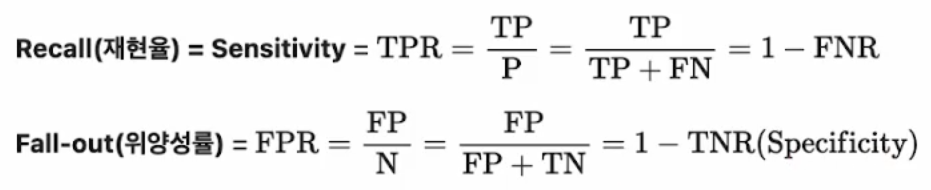
재현율(Recall, TPR)은 최대화 하고 위양성률(FPR, Fall-out)은 최소화 하는 임계값(Threshold)을 찾아내는 게 목적!!
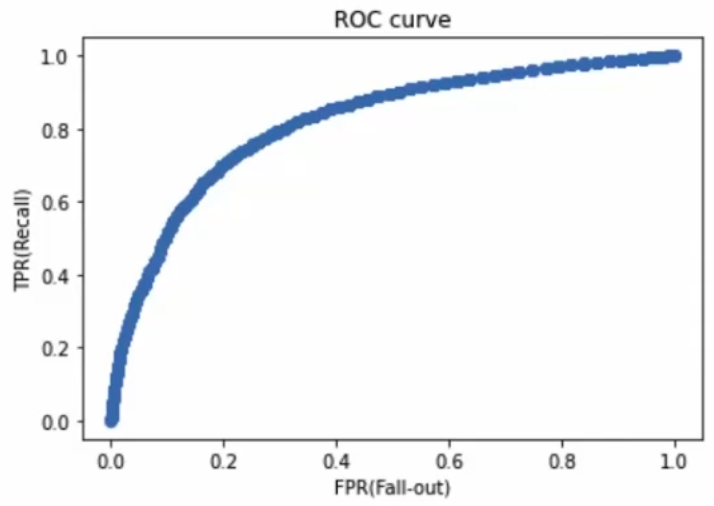
ROC curve가 좌상단에 밀접할 수록 좋은 모델!! = AUC 면적이 클 수록 좋은 모델!!
ROC curve는 이진분류 문제와 다중분류 문제에서 사용 가능. 다중분류 문제에서는 각 클래스를 이진클래스 분류문제로 변환(One vs All)하여 구할 수 있음.
Q&A
1. F1이 precision, recall의 조화평균이어서 가장 정확할 것 같은데, F1_Score 대신에 precision과 recall을 개별적으로 사용하는 경우가 있을까요?
- F_beta_score의 수식은 precision과 recall로 되어 있다.
- precision과 recall이 사용되는 곳이 f1 이외에 있는가?
→ TPR & FPR, 임계값(Threshold)
→ F1_Score 대신에 precision과 recall을 개별적으로 사용하는 경우가 있음.
2. 상황에 따라 precision 및 recall을 평가지표로 사용될 것 같은데 F1_Score를 봐야할까요? 어떤 경우에 어떤 평가지표를 중점적으로 봐야 하는 지 알고 싶습니다.
Accuracy와 Confusion Matrix, Precision, Recall, ROC_curve, AUC_score를 문제에 따라 종합적으로 봐야 한다!!
3. 정밀도 vs 재현율 예시
공산품 불량품 분류 → FN이 문제 → Recall을 유심히 본다.
접종 여부(1 = 접종) → FP가 문제
금융사기탐지, 약 부작용, 모조품 판별, 예약 취소 여부, 광고 대상자, 사기꾼 판별, 유형에 따른 마스크 착용 여부, 기타 등등
문제 설정이 매우 중요함!!
4. 보통 구하고자 하는 것을 1(Positive)로 설정하는 게 맞나요?
그렇다. 접종 여부를 예시로 보자면, 1 = 접종, 0 = 접종 X
5. 임계값이란?
엄격하게 판단하기 위한 기준!! 움직일 수 있다.
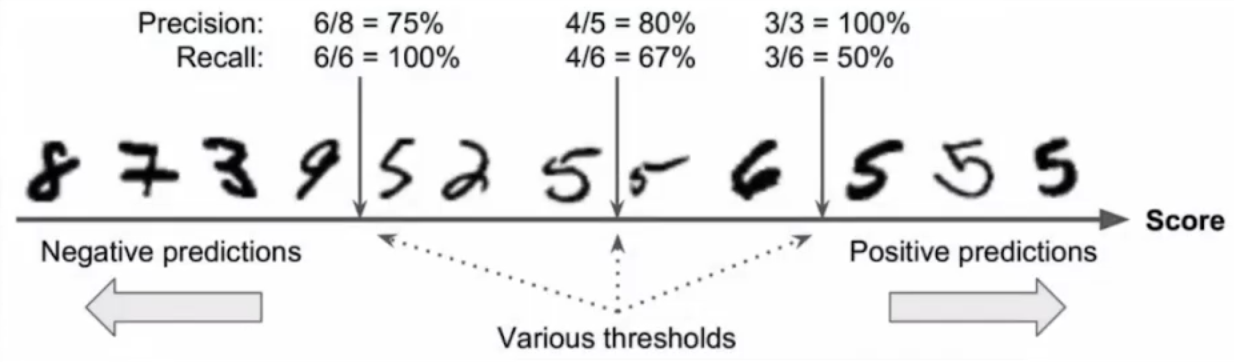
6. F_beta_score vs Threshold 차이점
beta → 모델 성능을 평가(train)
Threshold → 분류할 때 확률의 기준(연구자가 직접 엄격함을 정해주는 것)
7. '최적의 Threshold를 찾는다'에서 '최적'이 무엇에 대한 최적인가요? F1인가요?
???
8. 가중치는 어떤 기준으로 정하나요? 예컨대 beta 값이 2일 때 recall이 precision보다 중요한 것은 알겠는데 얼마나 중요한 것인지 가늠을 못 하겠습니다.
스스로 연구하라는 답변이었음.