Quaternions
Notation
-
회전을 표현할 때, 행렬 대신 사용하는 수학적 개념으로 4개의 값으로 이루어진 복소수 체계이다.
-
q=[qq] with q=[q1,q2,q3]T
-
q=q+q1i+q2j+q3k
(i,j,k는 허수)
-
i2=j2=k2=ijk=−1
-
오일러 각의 짐벌락 현상을 해결하기 위해 세 축을 차례대로 회전하는 대신 동시에 회전시키는 방식을 사용한다.
Rotation at complex plane
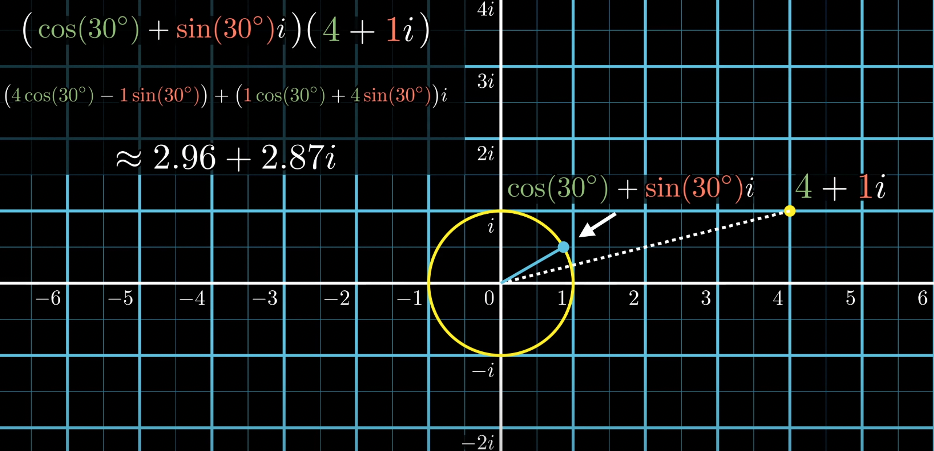
- 단위원에서 30도 회전의 좌표는 cos(30°)+sin(30°)i
- (cos(30°)+sin(30°)i)(4+1i)를 계산하여 복소평면에서 4+1i를 30도 회전한 좌표를 구할 수 있다.
Caculation of Quaternions
Addition(p=q+r)
⎣⎢⎢⎢⎡p0p1p2p3⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡q0+r0q1+r1q2+r2q3+r3⎦⎥⎥⎥⎤
Multiplication(p=qr)
⎣⎢⎢⎢⎡p0p1p2p3⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡q0r0−q1r1−q2r2−q3r3q1r0+q0r1−q3r2+q2r3q2r0+q3r1+q0r2−q1r3q3r0−q2r1+q1r2+q0r3⎦⎥⎥⎥⎤
Inverse
q=∣q∣2q∗
- q∗=[q−q]
- ∣q∣2=q02+q12+q22+q32
Rotation of Quaternions
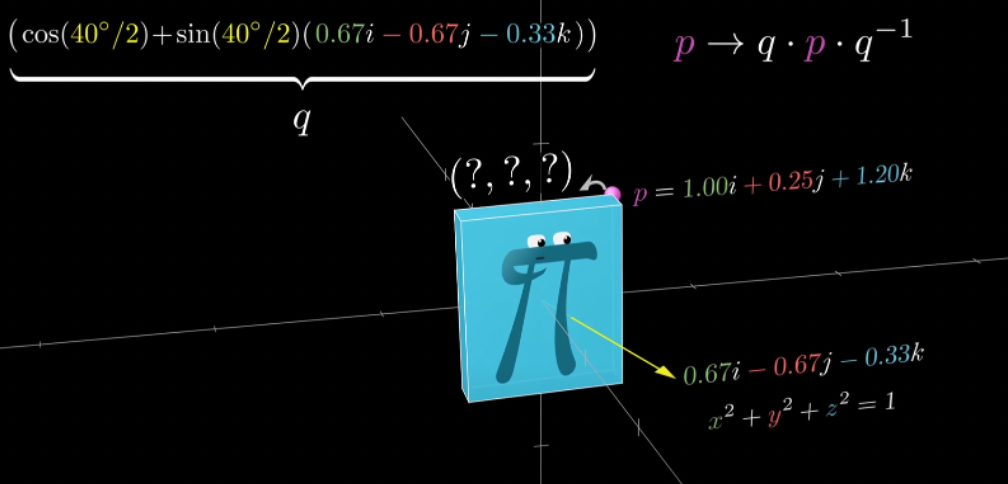
p′=qpq−1
- q=[qq]=[cos(θ/2)sin(θ/2)r]
- r=[r1,r2,r3]T with ∣∣r∣∣=1
- 정규화된 회전축 r을 중심으로 θ만큼 회전
Composition
- p′=q′pq′−1
- p′′=q′′p′q′′−1
- p′′=q′′q′pq′−1q′′−1
=(q′′q′)p(q′−1q′′−1)
=qpq−1
- q′ 회전 후 q′′ 회전을 하는 것은 multiplication 연산을 통해 q 회전으로 표현할 수 있다.
q=q′′q′
Materials
Reference


