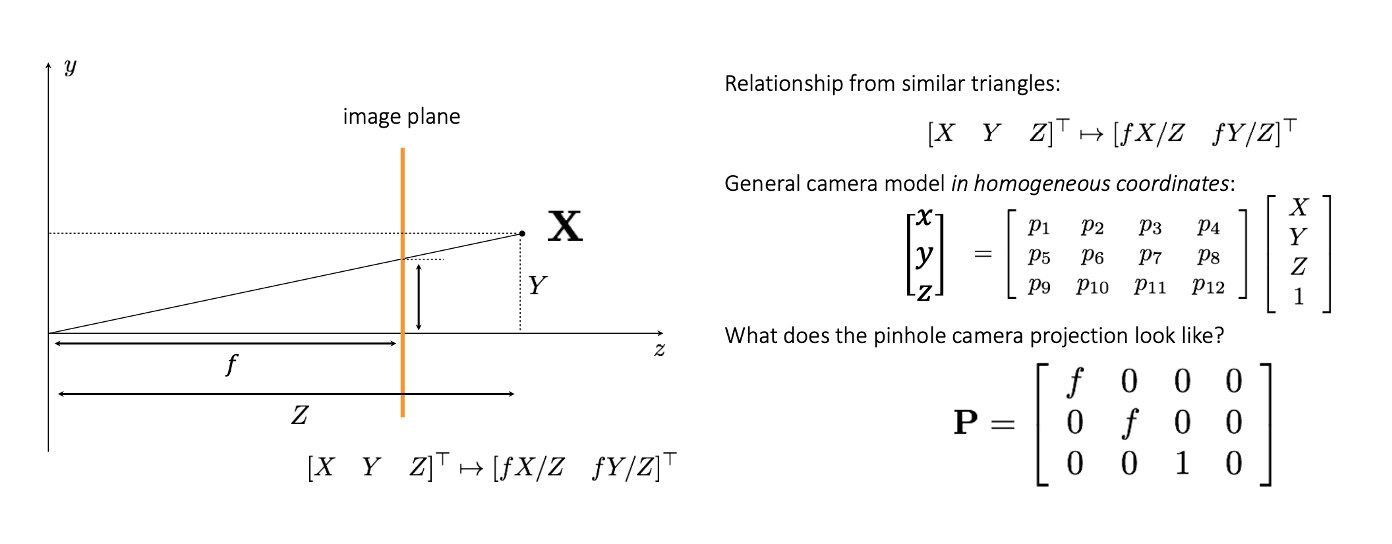
Pinhole camera matrix

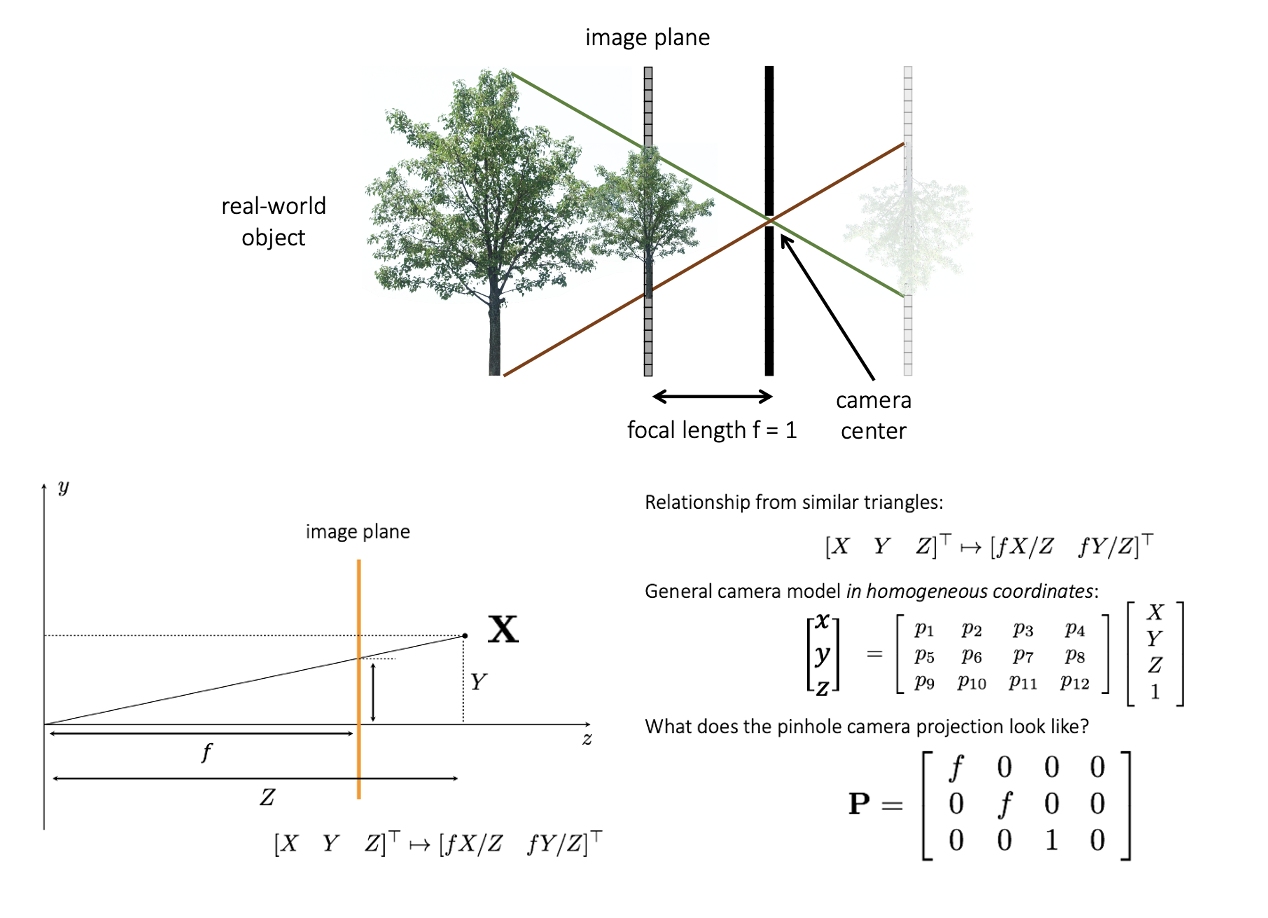
• Pinhole camera를 사용할 때 image plane에 맺히는 상은 뒤집힌 상태이기 때문에 object와 카메라 사이에 virtual image plane을 만든다.
• 3차원의 object를 2차원의 image plane에 투영시키는 행렬 $P$가 존재할 때 $x = PX$로 표현할 수 있다.
• 닮음 삼각형을 이용하면 $x=fX/Z$, $y=fY/Z$이므로 행렬 $P$를 위와 같이 쓸 수 있다.
• $f$(focal length)가 1일 때는 $P=[I|O]$가 된다.

Camera to image coordinate system

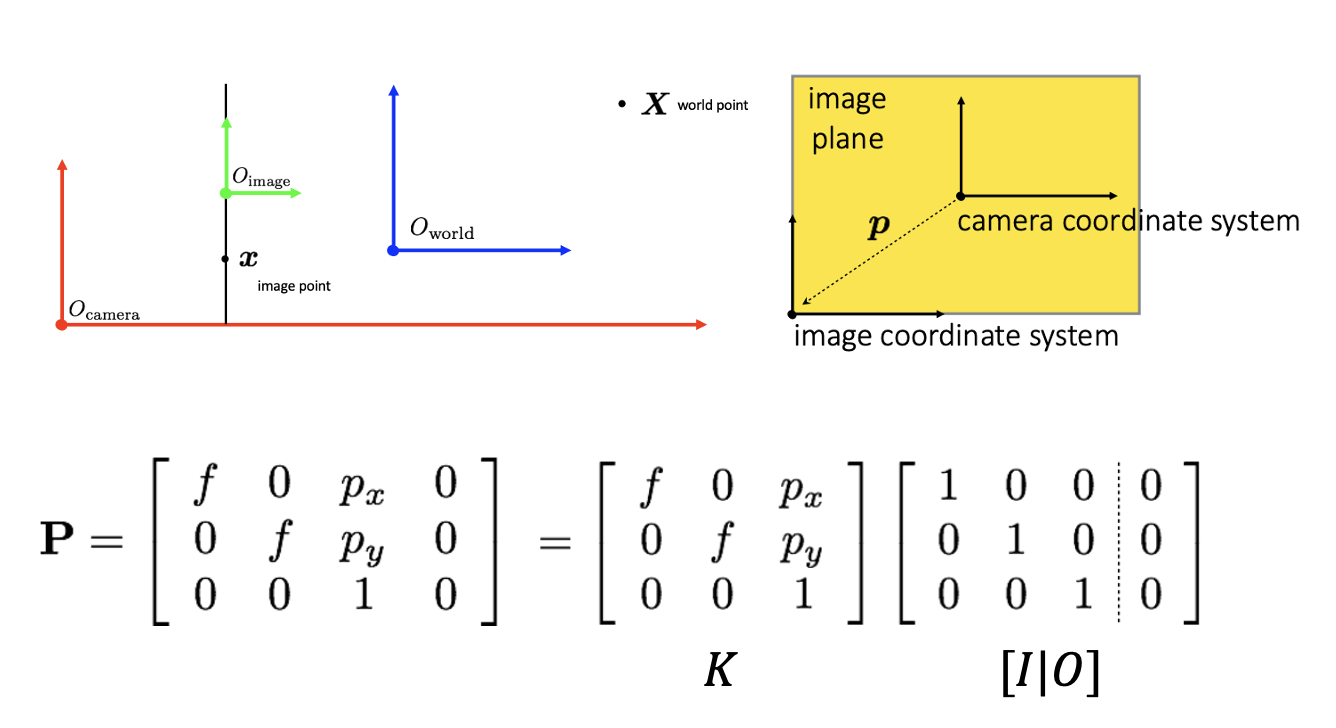
• 하지만, 일반적으로 카메라와 이미지의 좌표계는 다르기 때문에 카메라 좌표계를 구해주어야 한다.
• 카메라는 이미지의 중심에 위치 $p_x, p_y$로 shift하는 과정이 필요하다.
• $P$는 분해가 가능하며 $[I|O]$는 focal length가 1이라는 가정 하의 3D에서 2D로의 변환을, $K$는 focal length와 카메라 좌표계의 움직임을 표현한 2D에서 2D로의 변환을 의미한다.
• 이 때, $K$의 변수들을 intrinsic parameters라고 한다.

World to camera coordinate system

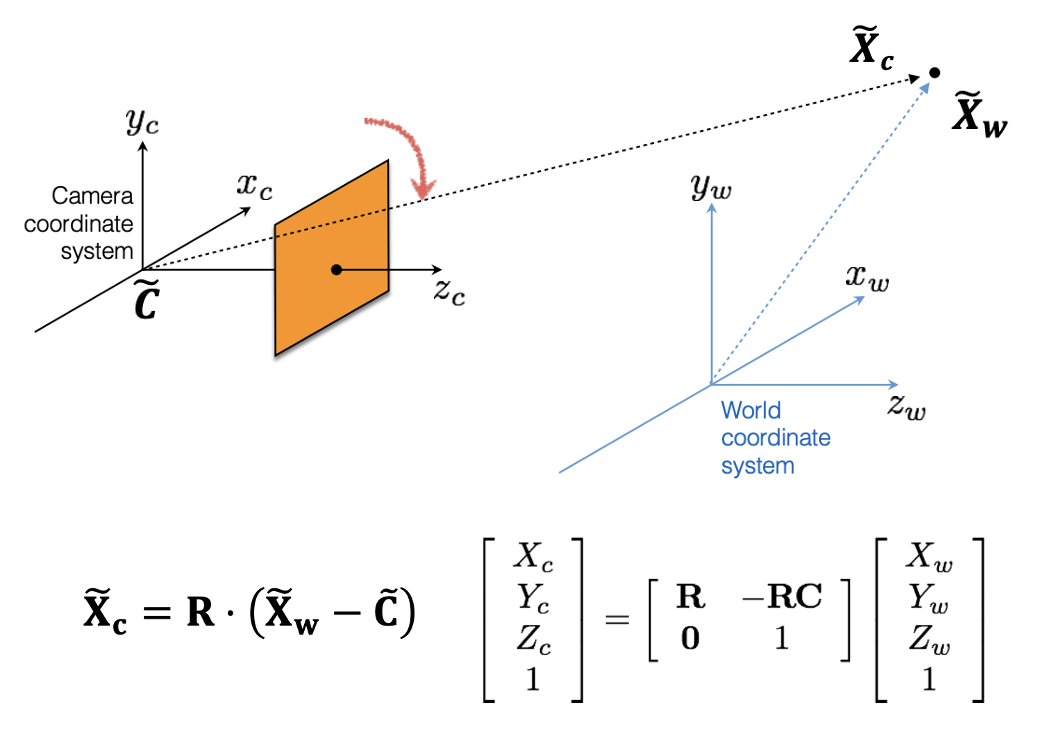
• World 좌표계와 카메라 좌표계는 다르기 때문에 $R$(Rotation)과 $\tilde{C}$(Tlanslation)을 통해 변환해준다.
• 이 때 homogeneous coordinate을 이용하기 때문에 선형식으로 표현할 수 있다.
• 위 과정에서 쓰이는 행렬의 변수들을 extrinsic parameters라고 한다.

Total system

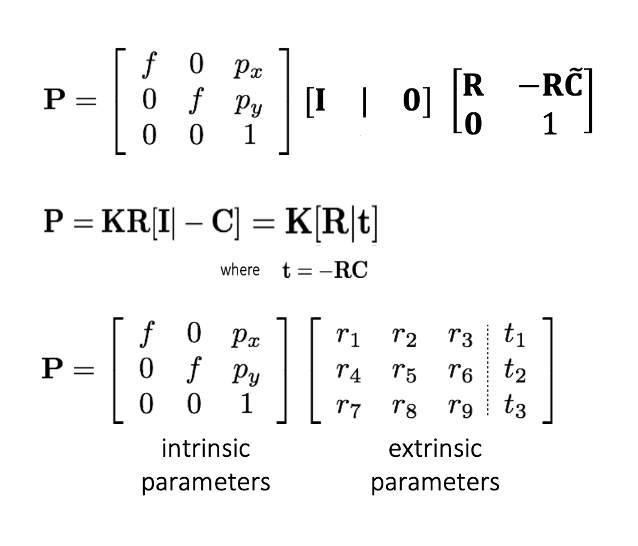
• Extrinsic parameters를 활용한 world to camera 변환과 intrinsic parameters를 활용한 camera to image 변환을 한꺼번에 표현하면 위와 같다.
• $K$의 2행 2열에는 공정상 오차로 이미지 센서가 y축으로 기울어진 정도인 $skew_c$가 있지만 최신 카메라들은 이 오차가 0에 가까워 고려하지 않는다.

강의

• linear camera model: https://www.youtube.com/watch?v=qByYk6JggQU
• CMU course: http://16385.courses.cs.cmu.edu/spring2022/