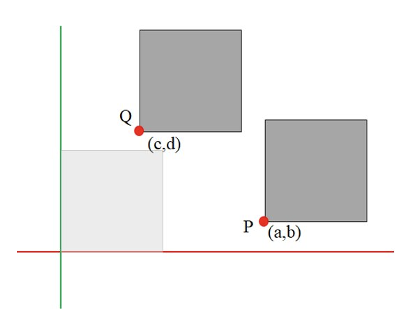
Vector space

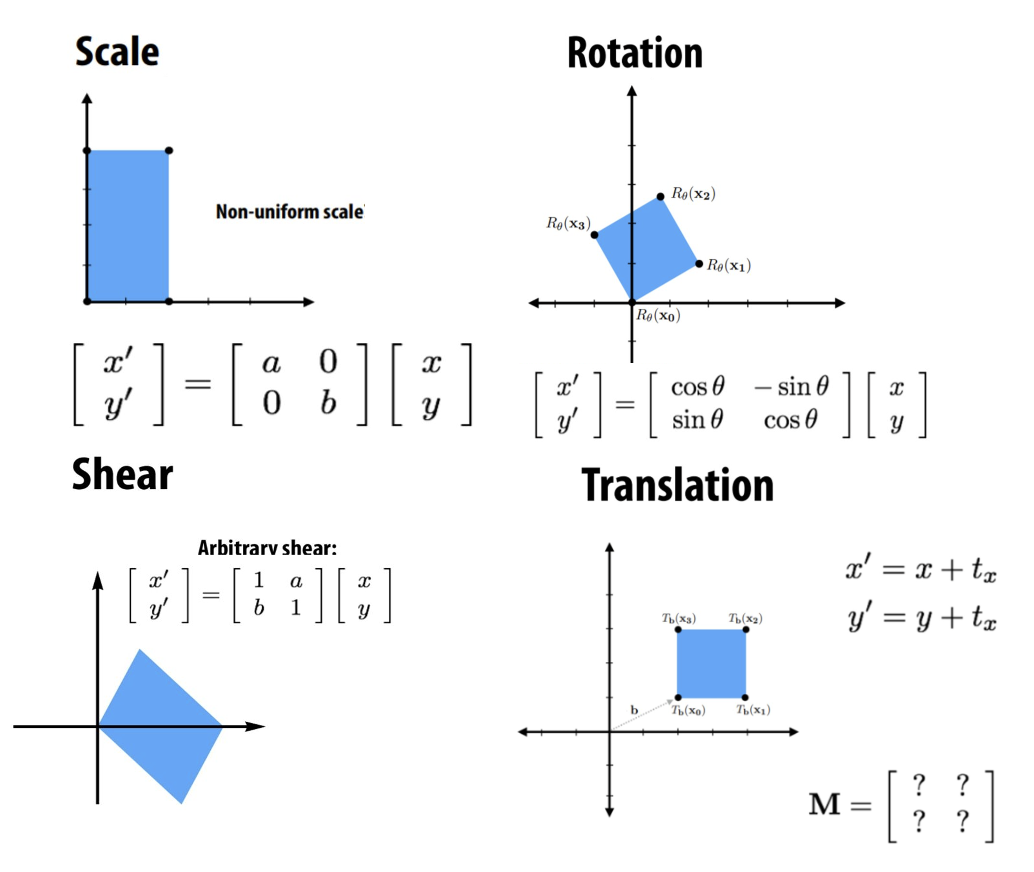
• Vector space에서의 값은 원점에서 뻗어나가는 방향을 의미하며 선형성(linearity)을 지닌다.
• 벡터의 위치와 관계없이 크기와 방향이 같다면 모두 같은 벡터로 인식되기 때문에 위치가 중요한 경우를 표현할 수 없다.
• Translation은 scale, rotation, shear과는 달리 vector space 내에서 transformation matrix를 정의할 수 없다
• 이를 해결하고자 차원을 추가하였고 Affine space, homogeneous coordinate가 탄생한다.

Affine space

• 위치 정보를 표현하기 위해 Affine space에서는 벡터에 점(Point)를 더해준다.
• $(a,b,0)$와 같이 마지막 값이 0인 경우는 vector, $(a,b,1)$과 같이 1인 경우는 point를 표현하는 것이 된다.

Affine sapce의 특징

• Affine space에 속한 모든 점 $P$에 대해서$P+\vec{0} = P+\vec{0} = P$이다. 즉, 영벡터는 벡터 공간의 항등원이다.
• Affine space에 속한 모든 점 $P$와 Vector space에 속한 모든 vector $v,w$에 대해서 $P+(v+w) = (P+v)+w$가 성립한다. 즉, 결합법칙이 성립한다.
• Affine space에 속한 점 $P,Q$가 있을 때, 두 점을 연결하는 vector는 단 하나이다

Tlanslation in Affine space

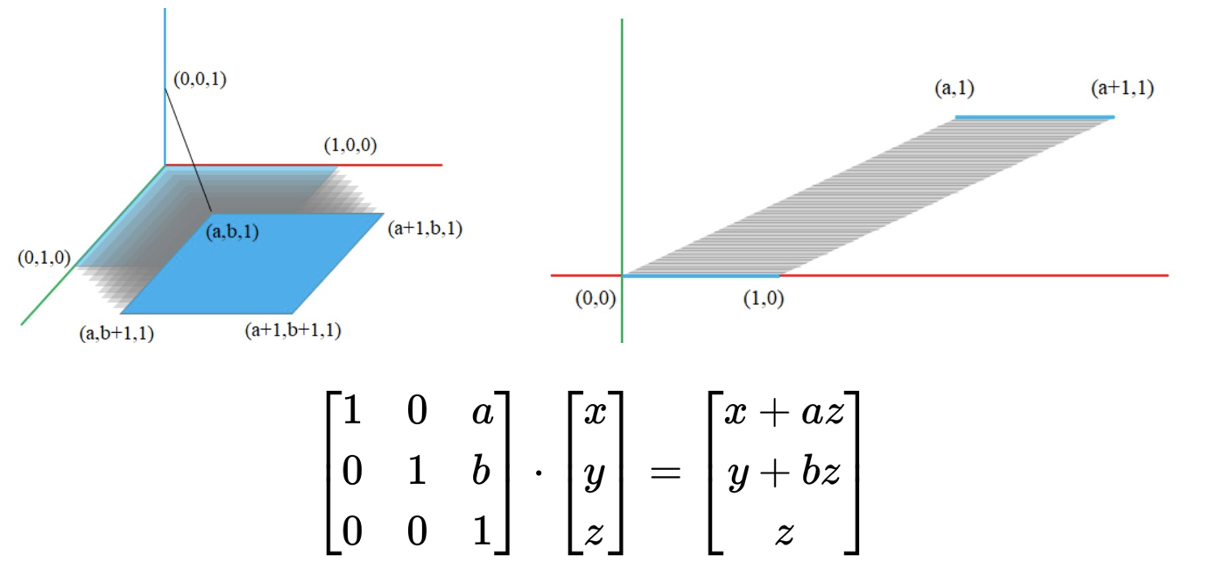
Affine space에서는 translation도 행렬로 표현할 수 있다.

Homogeneous coordinate

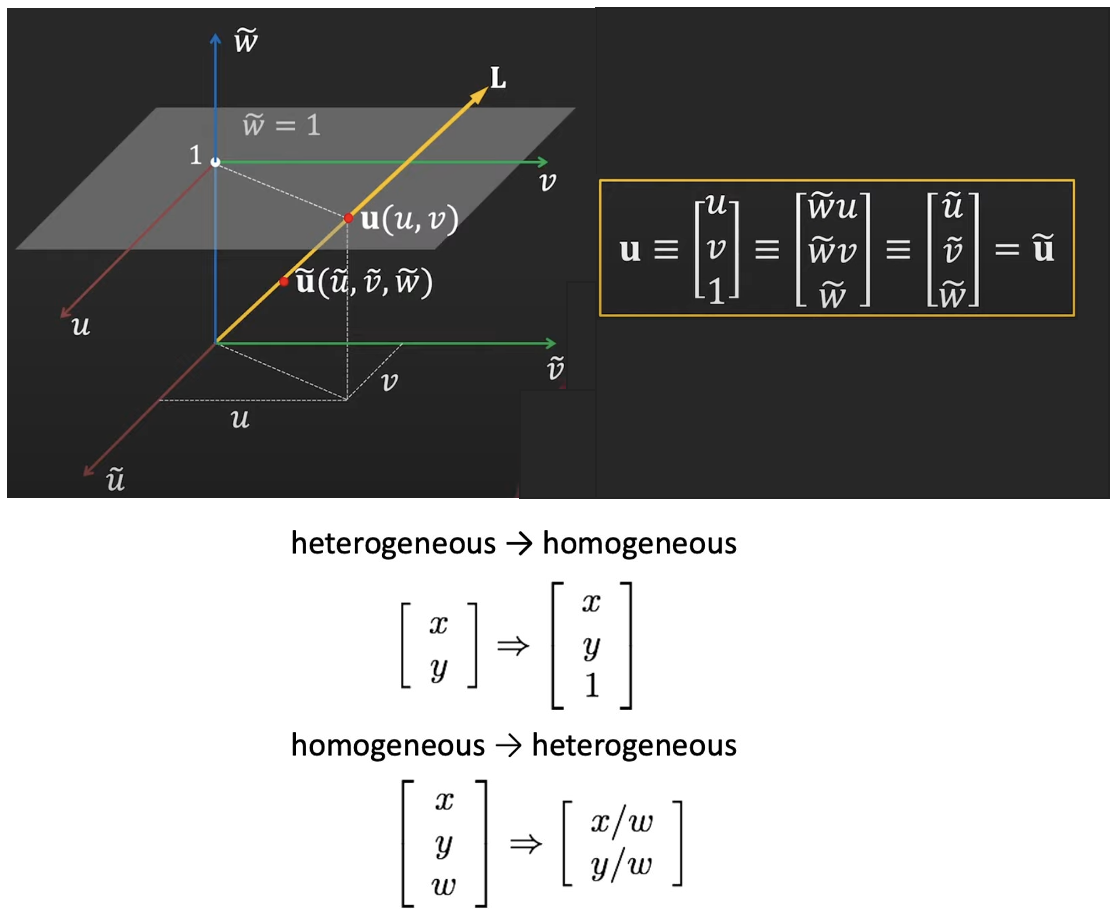
• 카메라의 ray는 무한대로 뻗어나가기 때문에 $P+\alpha$로 표현
• 이를 전부 표현하기 위해 homogeneous 좌표계에서 $(x,y)$는 $(wx,wy,w)$로 표기되어 scale을 무시하고 무한하게 존재하게 된다.
• 역으로 homogeneous 좌표에서 원래의 좌표를 구하기 위해서는 $w$로 나눠주면 된다.
• Homogeneous 좌표는 projection 좌표라고도 부르며 ray 상의 모든 좌표들은 하나의 평면에 투영시켜 표현할 수 있다는 점에서 의미가 있다.
• 3D 공간의 물체를 2D로 사영시킬 때 길이, 각도, 평행성은 보존되지 못한다.

강의

• linear camera model: https://www.youtube.com/watch?v=qByYk6JggQU
• CMU course: http://16385.courses.cs.cmu.edu/spring2022/

Reference

• https://darkpgmr.tistory.com/78