<CS224W> Lecture 12. Frequent Subgraph Mining with GNNs

김경준·2022년 4월 16일

CS224W Graph study

CS224W

목록 보기

12/17

1. Subgraphs and Motifs

Subgraph

Subgrpah는 노드와 엣지 중 어느 것을 중심으로 subset을 구성하냐에 따라 node-induced subgraph와 edge-induced subgraph로 나뉜다.
도메인에 따라 두 방식 중 하나가 선택되며 예를 들어 chemistry는 노드가 중요하므로 node-induced를 knowledge graph에서는 엣지가 중요하므로 edge-induced를 활용한다.
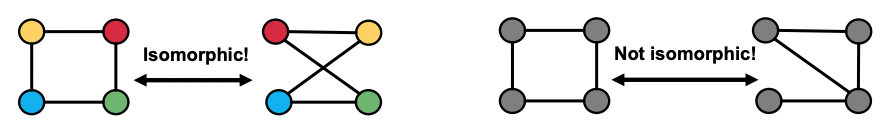
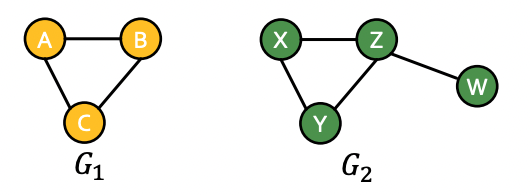
두 개의 그래프가 동일한지 확인하는 것은 중요한 문제이며 Graph isomorphism problem이라 한다.
그래프의 크기가 같더라도 엣지의 수 및 방향에 따라 다양한 non-isomorphic 그래프가 존재한다.

Network Motifs

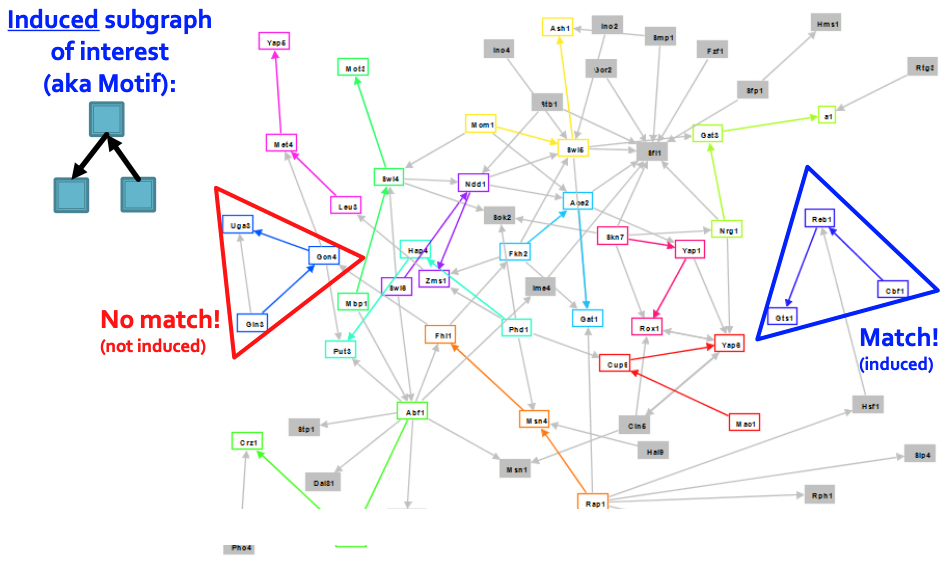
Network motifs는 "recurring, significant patterns of interconnections"로 정의된다.

1. Pattern: 찾고자 하는 node-induced subgraph로 motif이라고도 부르다.
2. Recurring: pattern이 전체 그래프에서 나타나는 빈도를 의미한다.
3. Significant: 랜덤하게 생성된 그래프에서 기대보다 빈번하게 있는가를 의미한다.

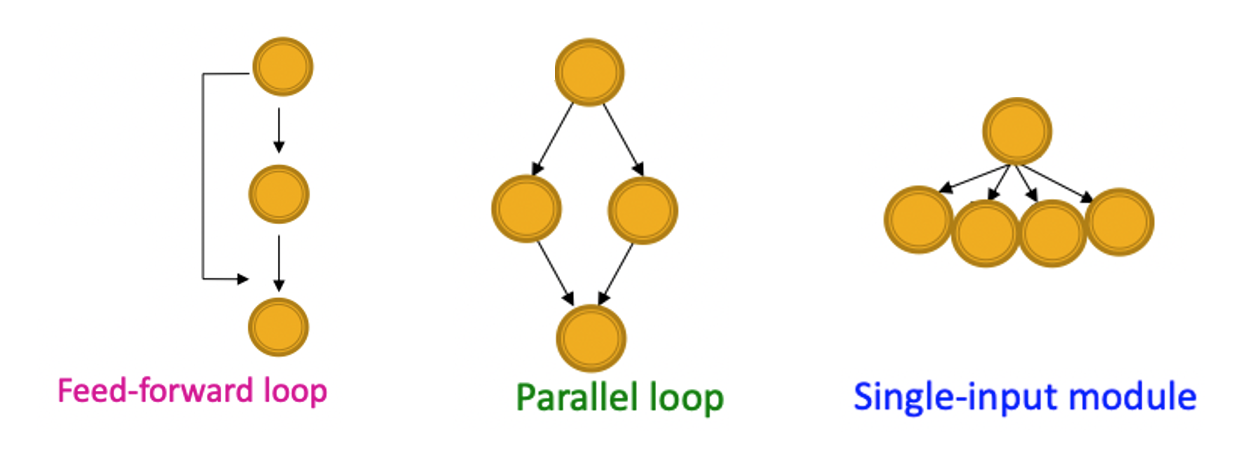
Motif을 통해 그래프의 작동방식을 이해할 수 있으며 예측하는데 도움이 된다.
예를 들어, feed-forward loop는 noise를 제거하는 용도로 뇌의 뉴런 네트워크에서 흔히 볼 수 있으며, parallel loops는 먹이사슬 관계에서 볼 수 있다.

Subgraph Frequency

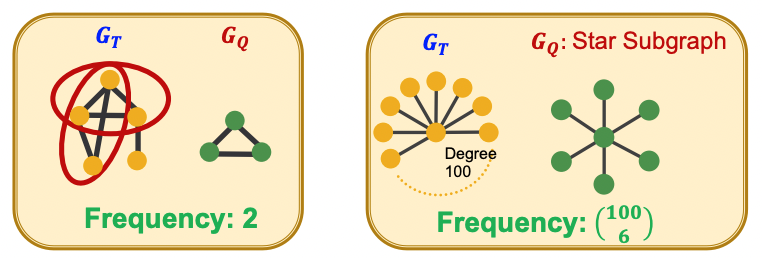
Graph-level에서는 거대 그래프 $G_T$ 에 포함되는 작은 그래프 $G_Q$ 의 개수로 빈도를 정의할 수 있다.
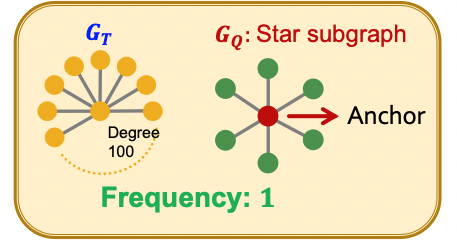
Node-level에서는 $G_Q$ 의 anchor 노드를 $v$ 라 할 때 $G_Q$ 와 isomorphicg한 $G_T$ 의 subgraph들 중 $u$ 로 맵핑되는 노드 $v$ 의 개수를 빈도로 정의한다.
이러한 방식은 outlier에 더 robust하다.
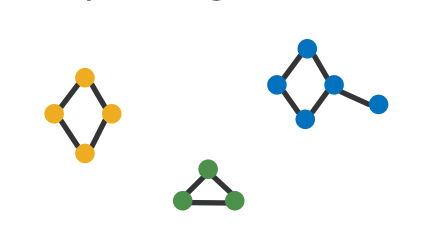
데이터셋이 여러개의 그래프를 가진다면 연결되지 않은 부분을 가진 하나의 거대 그래프 $G_T$ 로 보고 빈도를 계산한다.

Significance

Significance는 랜덤하게 생성된 네트워크에서의 motif 빈도보다 real nework의 빈도가 더 많을 것이라는 가정 하에 정의된다.
랜덤 네트워크를 만드는 방식에는 세가지가 있다.

Random Graph Generation

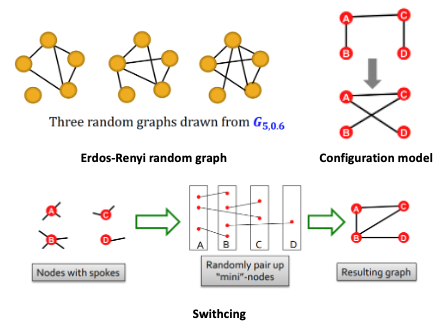
Erdos-Renyi random graph: $G_{n,p}$ 는 $n$ 개의 노드에서 확률 $p$ 에 의해 엣지를 랜덤하게 만들어주는 undirected graph이다.
Configuration model: Degree sequence를 이용하는 방법으로 같은 degree sequence를 가진 $G^{real}$ 과 비교할 수 있다. 각 노드는 degree만큼 랜덤하게 엣지를 연결하여 그래프를 생성한다.
Switching: 엣지 쌍을 무작위로 선택하여 endpoint를 바꿔 새로운 그래프를 생성한다. 비교될 그래프와 node degree가 같다는 특징이 있다.

Z-score for Statistical Significance

$Z_i = (N_i^{real}-\bar N_i^{rand})/std(N_i^{rand})$
$N_i^{real}$ 은 $G^{real}$ 에서 motif $i$ 의 수, $\bar N_i^{rand}$ 는 random graph들의 motif $i$ 의 수의 평균이다.
$S P_{i}=Z_{i} / \sqrt{\sum_{j} Z_{j}^{2}}$
Significance에 대한 통계학적 지표는 정규화된 z-score의 벡터로 나타낸다.
$SP_i$ 의 차원은 motifs의 수가 된다.
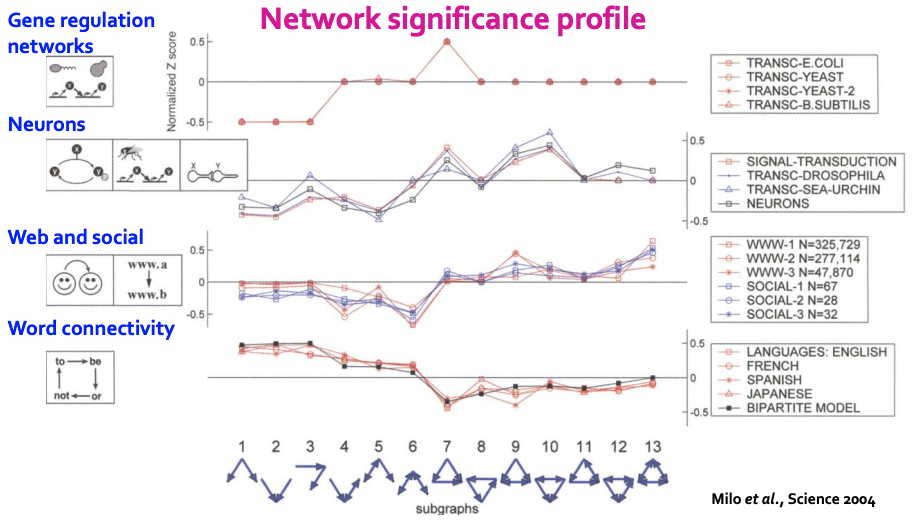
위와 같은 network significance profile을 만들 수 있다.
도메인에 따라 서로 다른 모습을 가지는 것을 확인할 수 있다.

2. Neural Subgraph Matching

Subgraph Matching

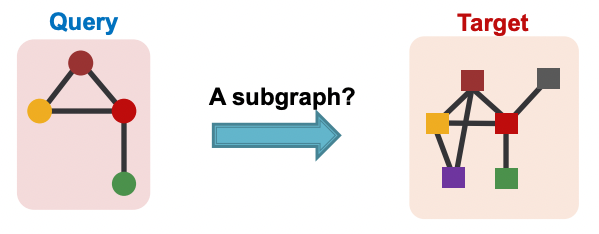
Subgraph matching이란 query 그래프가 target 그래프의 subgraph isomorphism인지 확인하는 task이다.
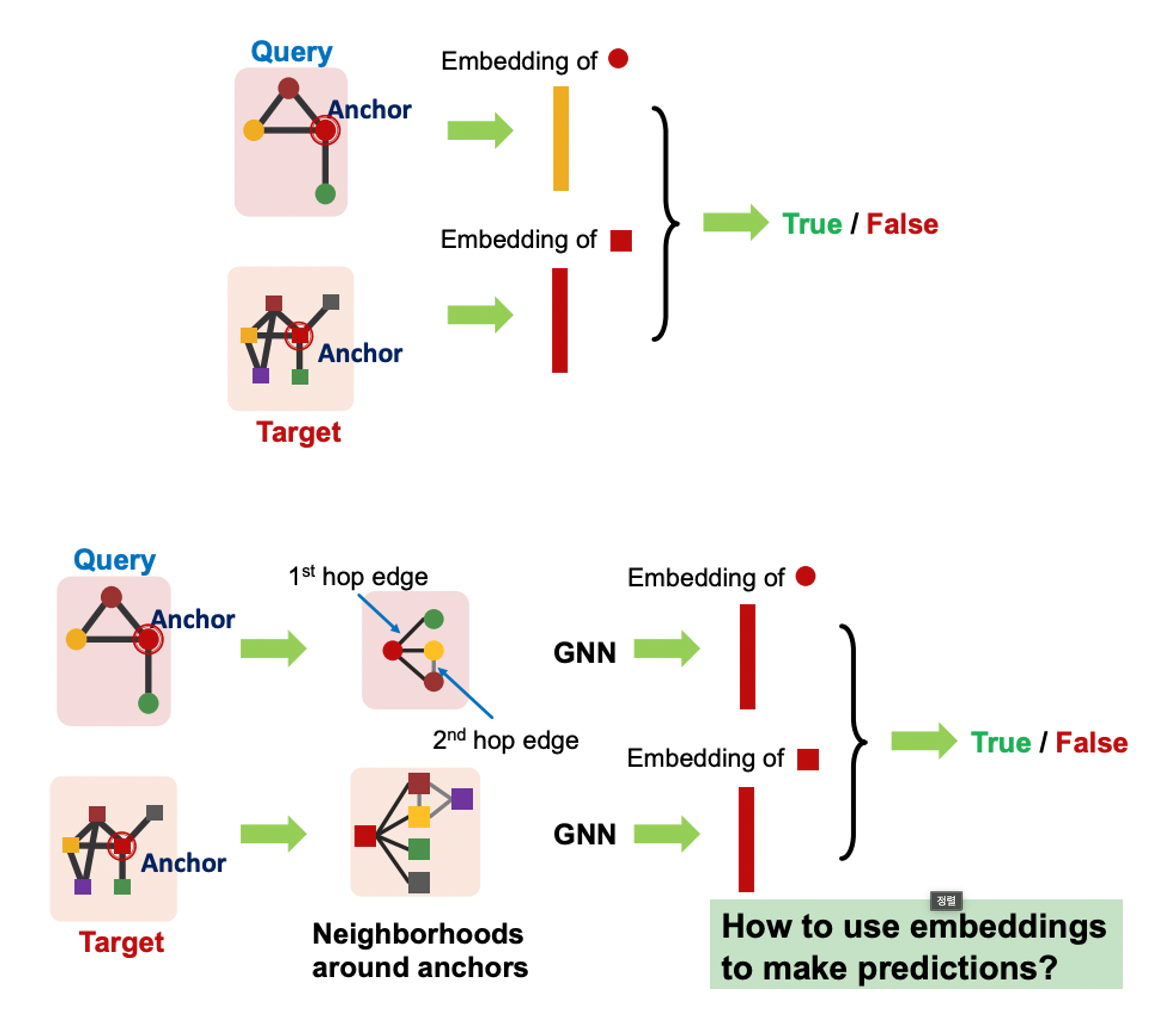
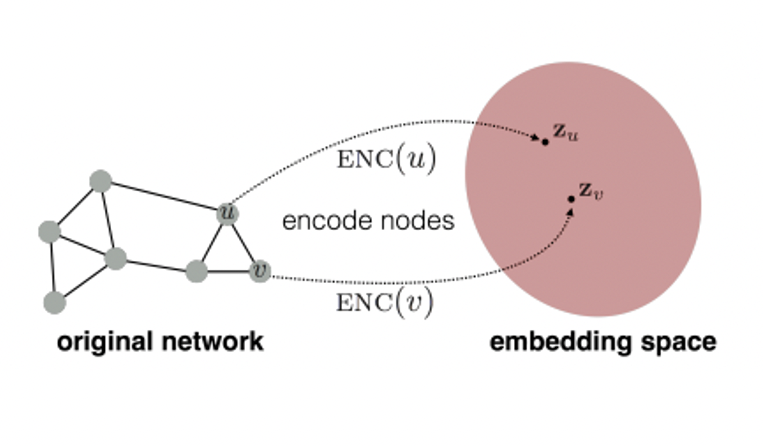
Node anchor를 활용하여 query의 노드 $v$ 와 target의 노드 $u$ 의 임베딩이 동일한지 확인한다.
Query의 anchor node가 n-hop을 가질 때 n-hop 내에 있는 이웃노드들의 임베딩 또한 비교한다.

Order Embedding Space

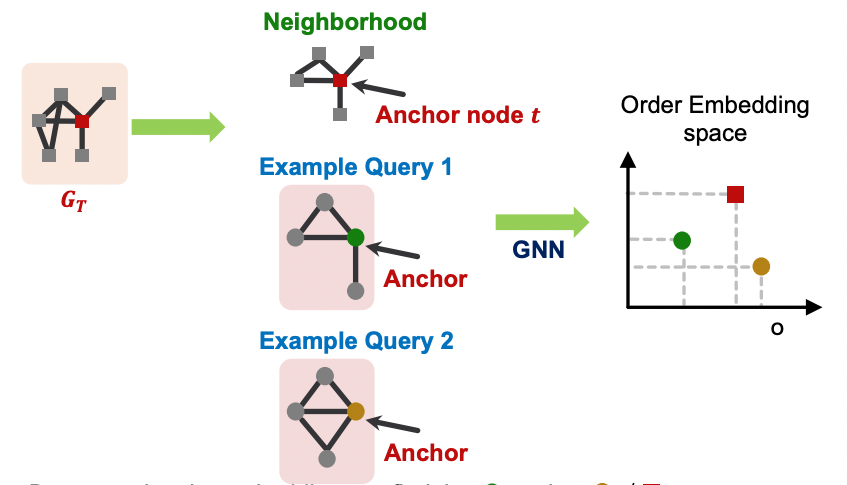
임베딩 공간에서 두 그래프 중 하나가 다른 하나의 좌하단에 위치한다면 subgraph임를 의미한다.

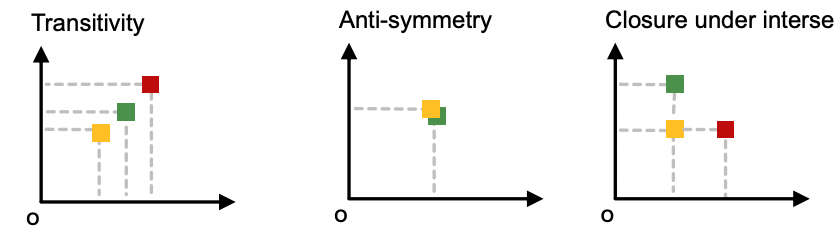
Transitivity: $G_1$ 이 $G_2$ 의 subgraph이고 $G_2$ 가 $G_3$ 의 subgraph라면 $G_1$ 은 $G_3$ 의 subgraph이다.
Anti-symmetry: $G_1$ 이 $G_2$ 의 subgraph이고 $G_2$ 가 $G_1$ 의 subgraph라면 두 그래프는 isomorphic하다.
Closure under intersection: 노드가 하나인 그래프는 모든 그래프의 sugraph이다. 음수를 가지는 임베딩은 없으며 $a \le b$ , $a \le c$ 라면 $a$ 는 유효한 값을 가진다.

Loss Function

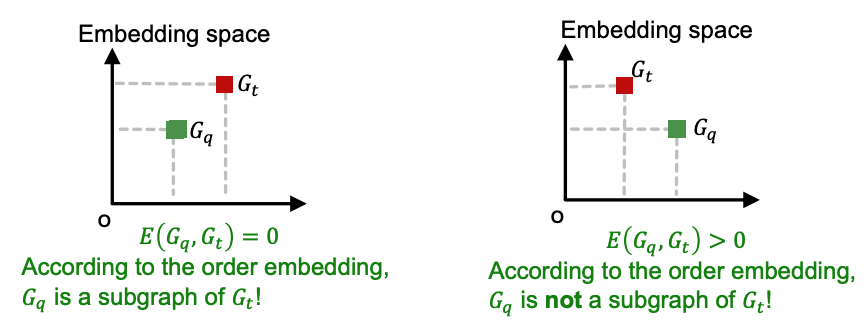
위와 같은 순서관계를 잘 보존하는 임베딩을 만들기 위한 max-margin loss를 사용한다.
$E\left(G_{q}, G_{t}\right)=\sum_{i=1}^{D}\left(\max \left(0, z_{q}[i]-z_{t}[i]\right)\right)^{2}$
$G_q$ 가 $G_t$ 의 subgraph라면 loss가 0, 그렇지 않으면 loss가 양수가 된다.

Training

학습 데이터셋 $(G_q, G_t)$ 는 $G_t$ 의 subgraph인 $G_q$ 가 반, 그렇지 않은 것이 반이 되도록 구성해야 한다.
Positive sample에 대해서는 $E(G_q, G_t)$ 를 최소화하도록 negative smaple에 대해서는 $max(0, \alpha - E(G_q, G_t)$ )를 최소화하도록 학습하는데 이는 모델이 임베딩을 너무 멀리 이동시키는 것을 방지하기 위함이다.
데이터셋 $G$ 로부터 학습을 위한 $G_T$ 와 $G_Q$ 를 샘플링하는 과정이 필요하다.
$G_T$ 는 무작위로 anchor 노드 $v$ 를 뽑은 뒤 거리가 $K$ 인 모든 노드를 포함시켜 만든다.
Positive example $G_Q$ 는 BFS 샘플링을 거친다.
1. $S={v}, V = \phi$ 로 초기화한다.
2. 매 스텝마다 $S$ 의 모든 이웃 노드 집합 $N(S)$ 의 10%를 샘플링하여 $S$ 로 업데이트하며 나머지 노드들은 $V$ 로 업데이트 한다.
3. $K$ 스텝을 거치면 $G_Q$ 를 얻게 된다.
Negative example은 $G_Q$ 로부터 노드/엣지들은 제거하거나 추가하여 만든다.

3. Finding Frequent Subgraphs

Problem

가장 빈도가 높은 motif을 찾는데는 구성할 수 있는 subgraph의 종류가 매우 많고 그 그래프들이 $G_T$ 에서 나타나는 빈도를 세는데 드는 연산량이 매우 크다는 문제가 있다.
따라서, representation learning을 통해 임베딩 공간 내에서 GNN을 활용하고자 한다.

SPMinier

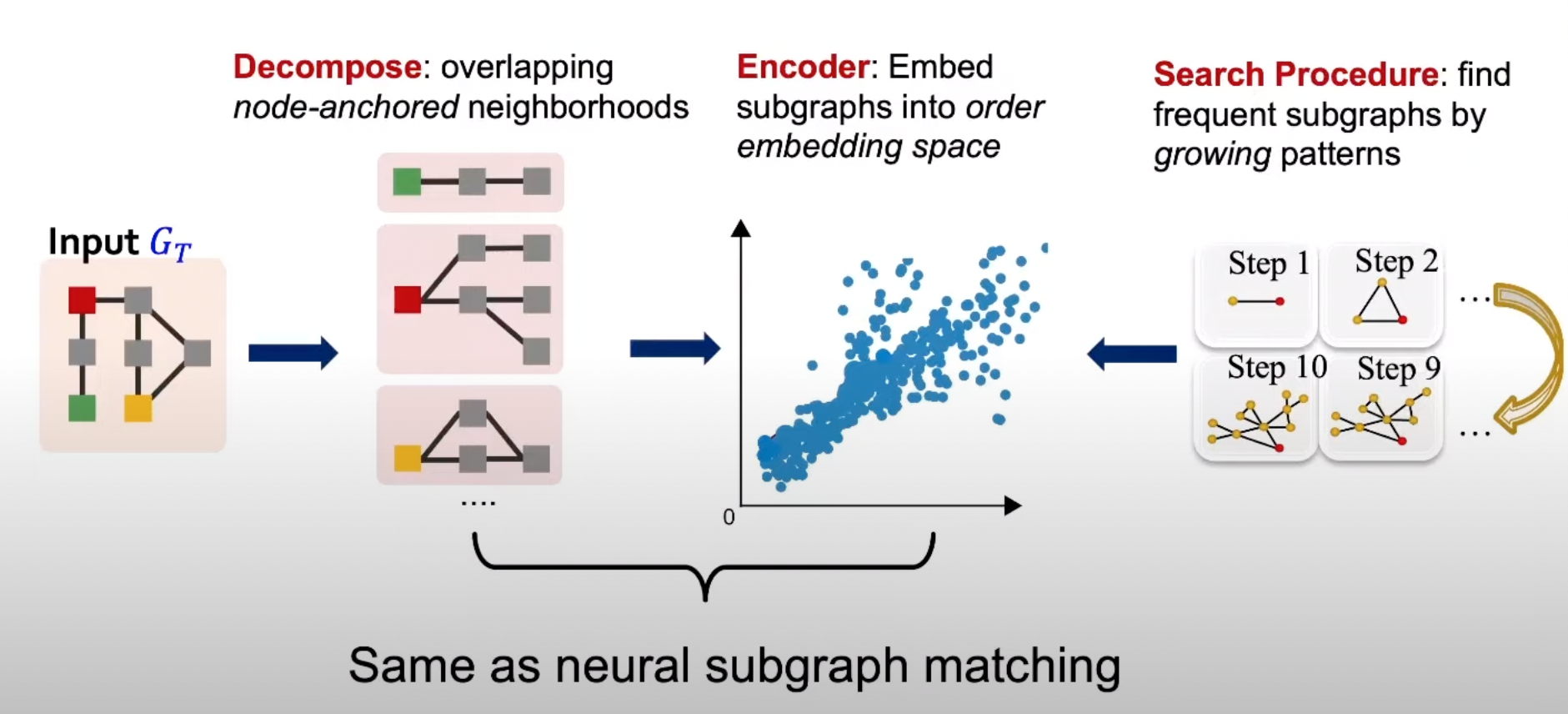
입력 그래프 $G_T$ 를 분해하여 order embedding space로 보낸뒤 subgraph들의 빈도를 확인한다.
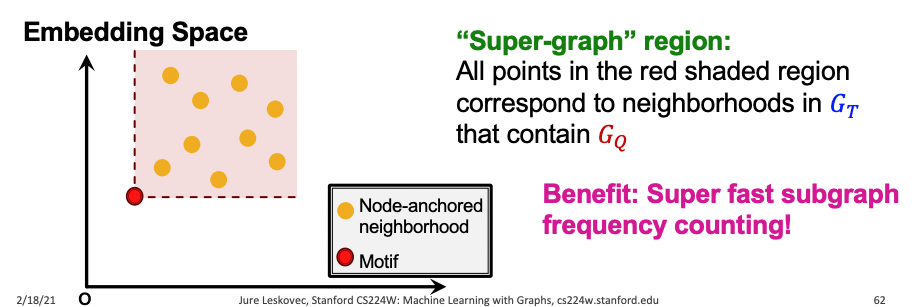
Order embedding space에서는 subgraph의 여부를 쉽게 알 수 있으며 위 그림에서 붉은색 영역 내의 모든 노란 점들은 $G_Q$ 를 포함하는 모든 $G_T$ 의 neighborhoods가 된다.
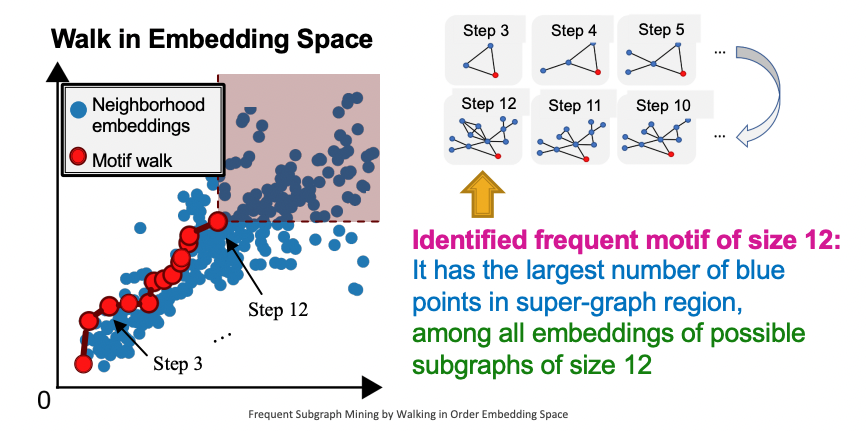
무작위로 선택한 노드 $u$ 로부터 시작하며 $S={u}$ 로 설정한다.
Motif의 사이즈는 $S$ 의 이웃 노드들을 골라 점진적으로 늘리며 $k$ 스텝 후에 붉은 영역에 속하는 neighborhoods의 수를 최대화하는 것이 목적이다.
원했던 motif size에 도달하면 멈추고 $S$ 로부터 subgraph를 도출한다.