1. Community Detection in Networks
Granovetter's Answer
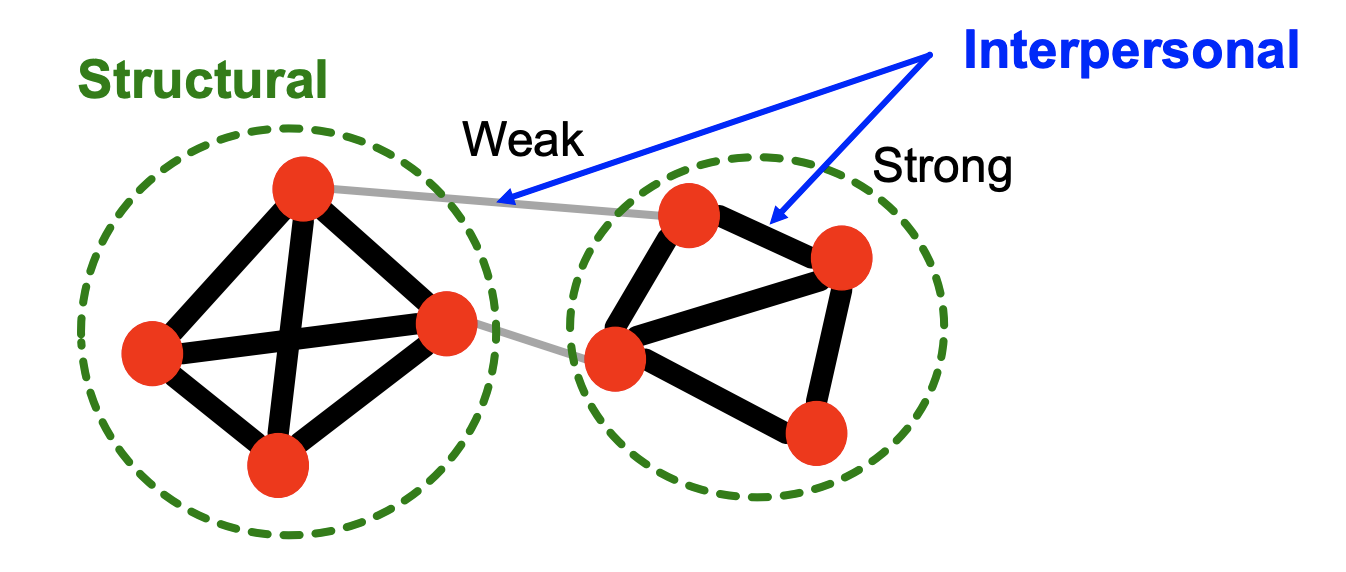
- Social network에서의 관계는 가까운 친구와 지인으로 나뉠 수 있다.
- 구직을 하는 과정에서 친한 친구보다는 지인으로부터 소개를 받는 경우가 많다.
- Granovetter는 엣지의 사회적인 역할과 구조적인 역할의 관계를 다음과 같이 나타냈다.
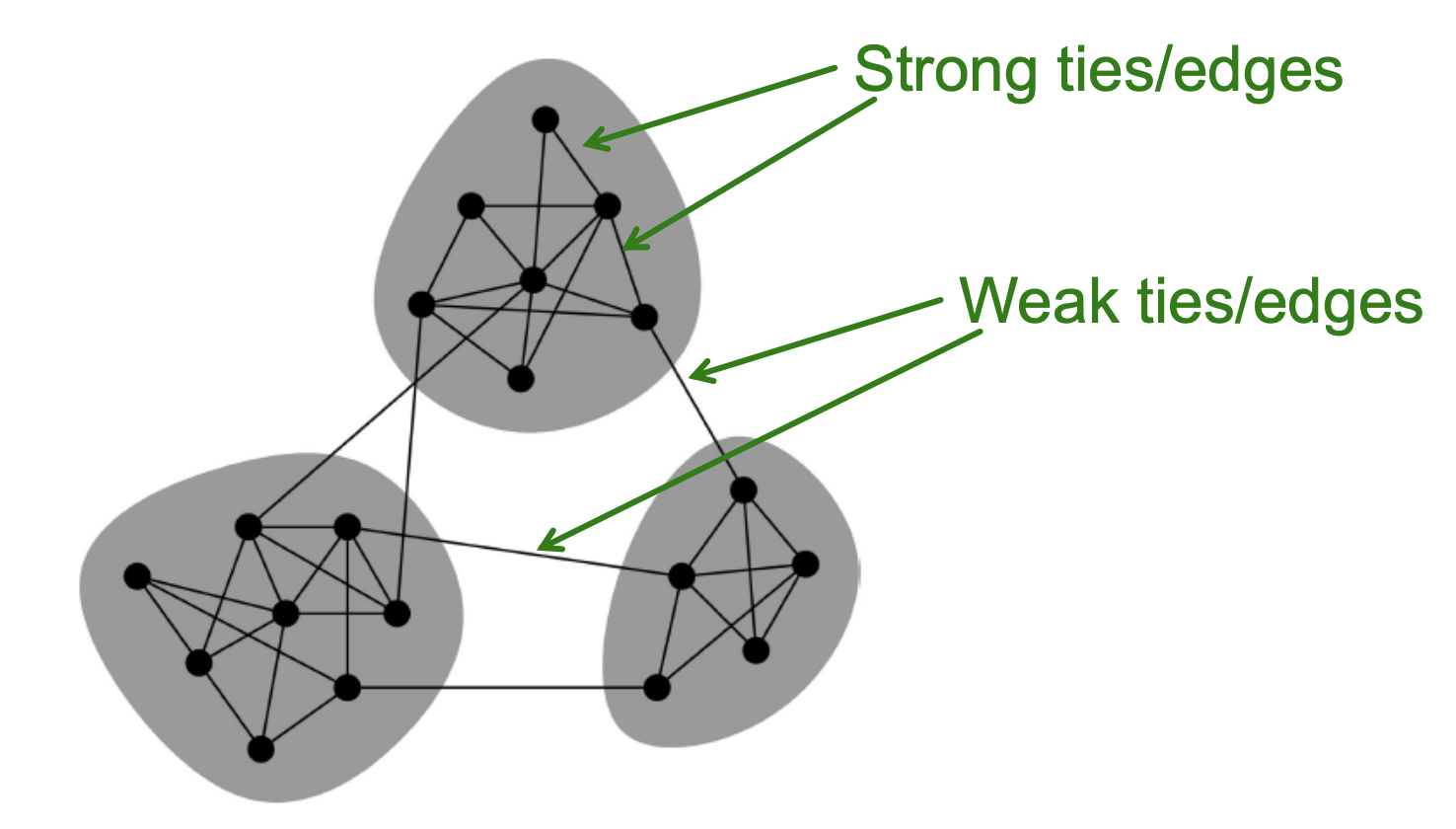
Structure: Structually embedded(밀접하게 연결된) 엣지는 사회적으로도 강하게 연결되며 다른 part를 연결하는 logn-range 엣지는 사회적으로 약한 연결 관계에 있다.
Information: Long-range 엣지는 다른 part의 정보를 얻는데 용이하며 structually embedded 엣지는 정보의 접근이 어렵다.
Triadic Closure
- Triadic closure = High clusetering coefficient
- 와 가 공통적으로 를 친구로 두고 있을 때 가 와 만날 확률은 높아지고 서로를 비교적 더욱 신뢰할 수 있으며 는 두 친구를 함께 데려올 수 있다.
Edge Overlap
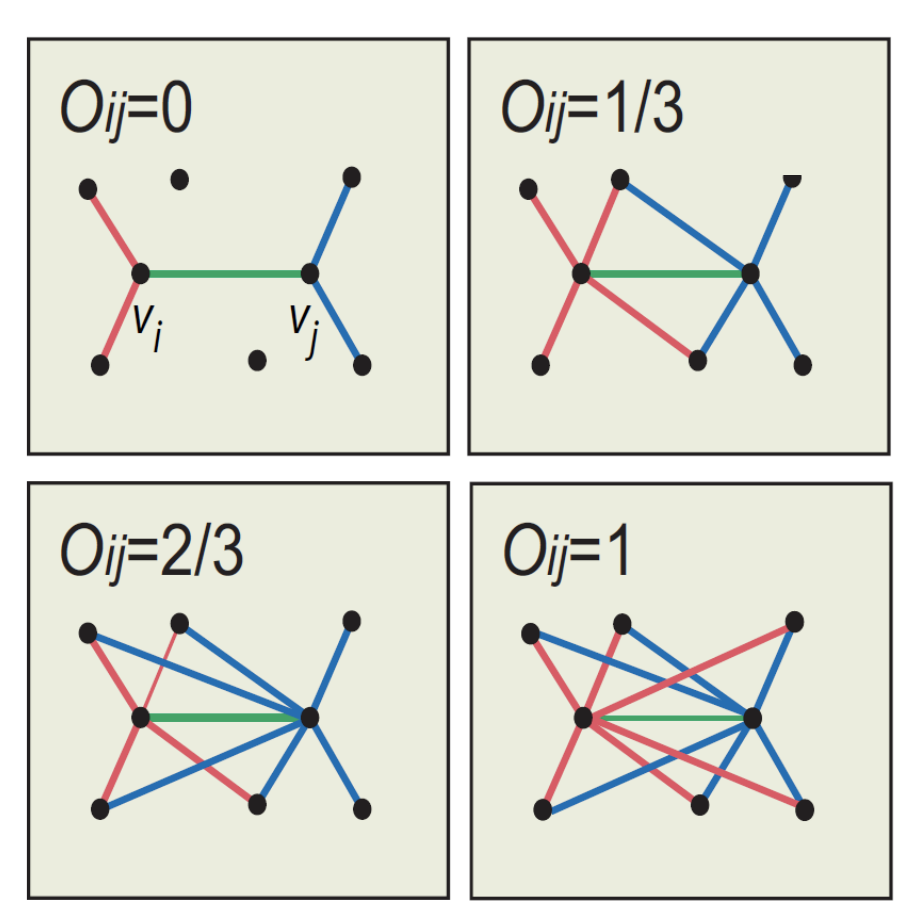
-
오랜 기간 test 되지 않았던 Granovetter의 이론은 Onnela가 통화횟수을 edge weight로 정의하고 휴대폰 네트워크에 대해 분석함으로써 증명되었다.
-
(Edge overlap)은 두 사람이 얼마나 많은 지인을 공유하는가에 대한 정보를 제공한다.
, 는 노드 의 이웃노드 집합
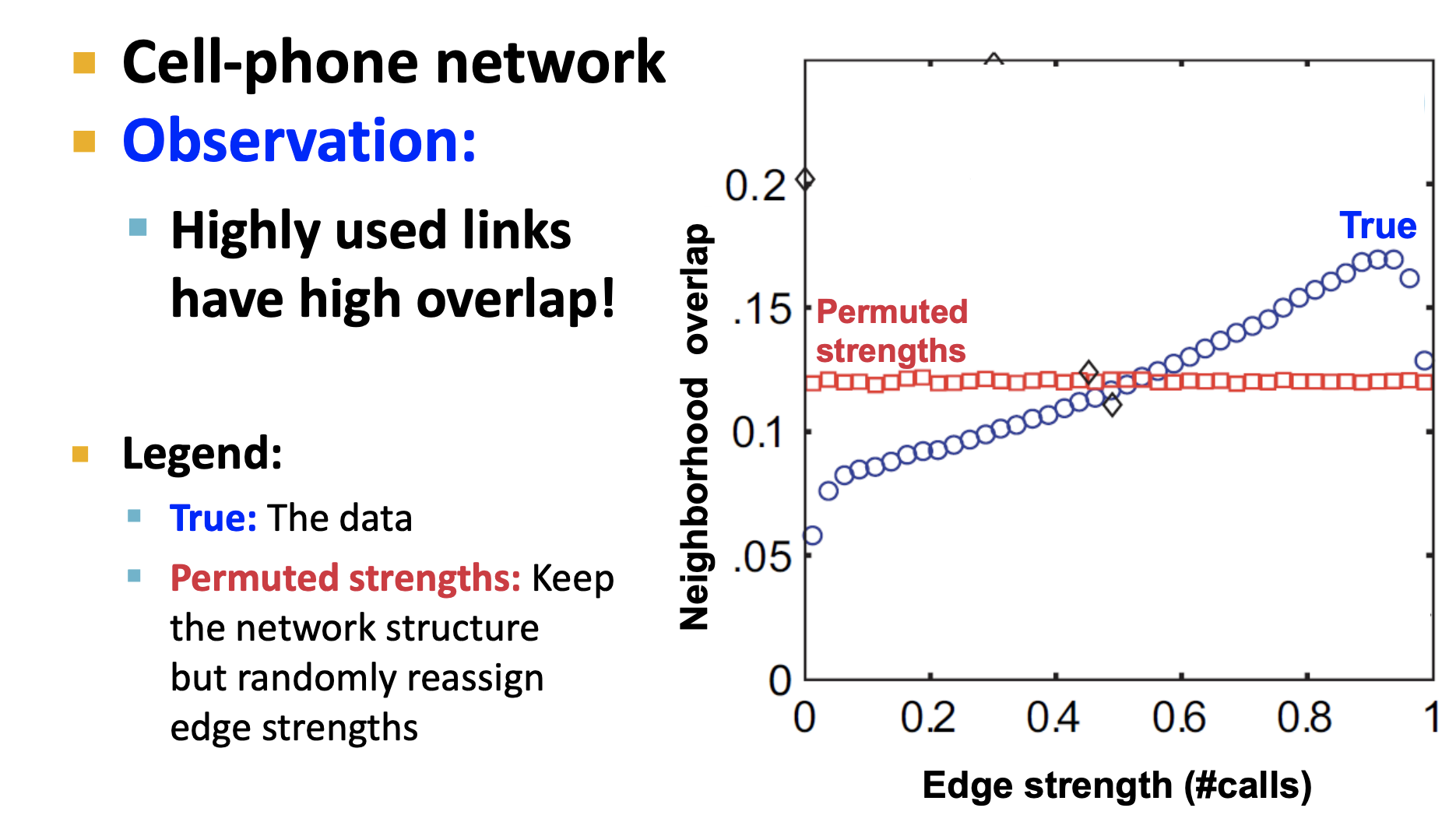
-
결과가 의미하는 바를 정확히 이해 못했지만 네트워크가 밀접하게 연결된 노드들의 집합들로 구성됨을 보인다고 한다..
2. Network Communities
- Communities: 밀접하게 연결된 노드들의 집합
- Modularity : 네트워크가 communities로 얼마나 잘 나뉘었는지 측정하는 척도로 모든 partition에 대해 [group 내의 엣지의 수-기대 엣지의 수]의 합으로 정의한다.
[(# edges within group ) - (expected # edges within group )]
Null Model: Configuration Model
- Modularity 계산 시 필요한 기대 엣지에 대한 비교 그래프를 생성한다.
- 개의 노드와 개의 엣지로 구성된 로부터 동일한 degree 분포와 총 엣지의 수를 가지지만 uniformly random connections와 두 노드 사이의 multi edges가 가능한 을 만든다.
- 의 degree를 가지는 노드 의 기대 엣지 수는
이다.
-> 노드 에서 나가는 엣지들 개가 노드 로 향할 확률이 이기 때문. 은 directed edges를 의미한다. - 의 총 기대 엣지 수는 와 동일하게 유지된다.
Modularity
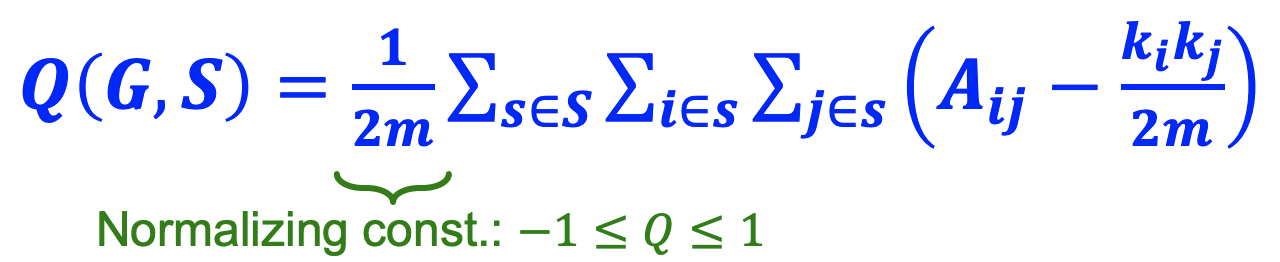
- Modularity의 값은 -1 ~ 1 사이의 값으로 정규화된다.
- Group 내의 엣지의 수가 기대 엣지 수보다 크면 양수이며 가 0.3~0.7 이상일 때 community를 이룬다고 본다.
- Weighted 네트워크에 대해서도 적용 가능하다.
3. Louvain Algorithm
- Community detection을 위한 그리디 알고리즘으로 시간복잡도는 이다.
Phase 1
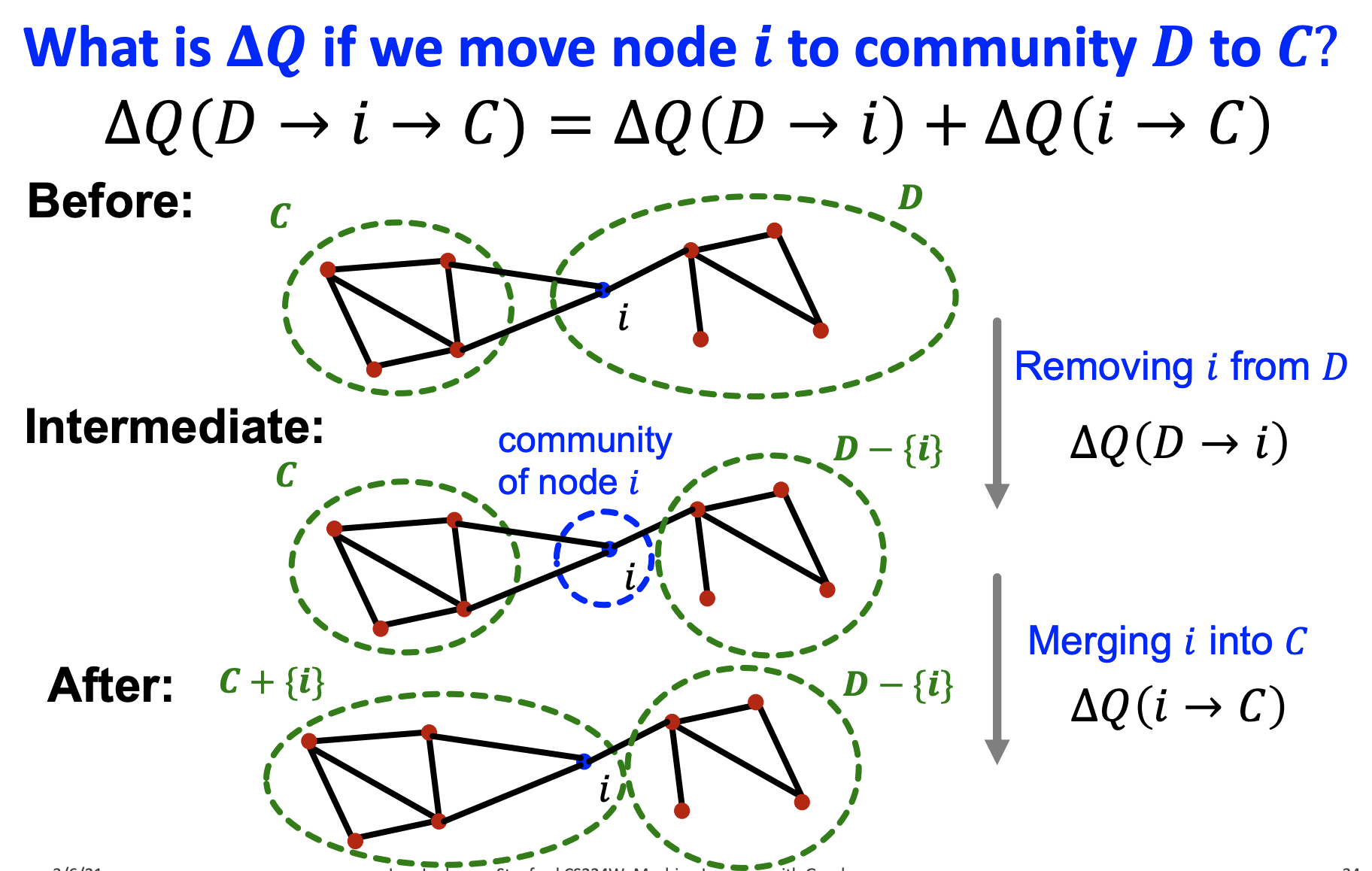
- 모든 노드를 각각의 community라고 생각한다.
- 노드 를 이웃노드 의 community로 옮길 때 발생하는 modularity의 증가량 를 구한다.
- 노드 를 가 가장 큰 community로 이동시킨다.
- 의 변화가 없을 때까지 위 과정을 반복한다.
Phase 2(Restructuring)
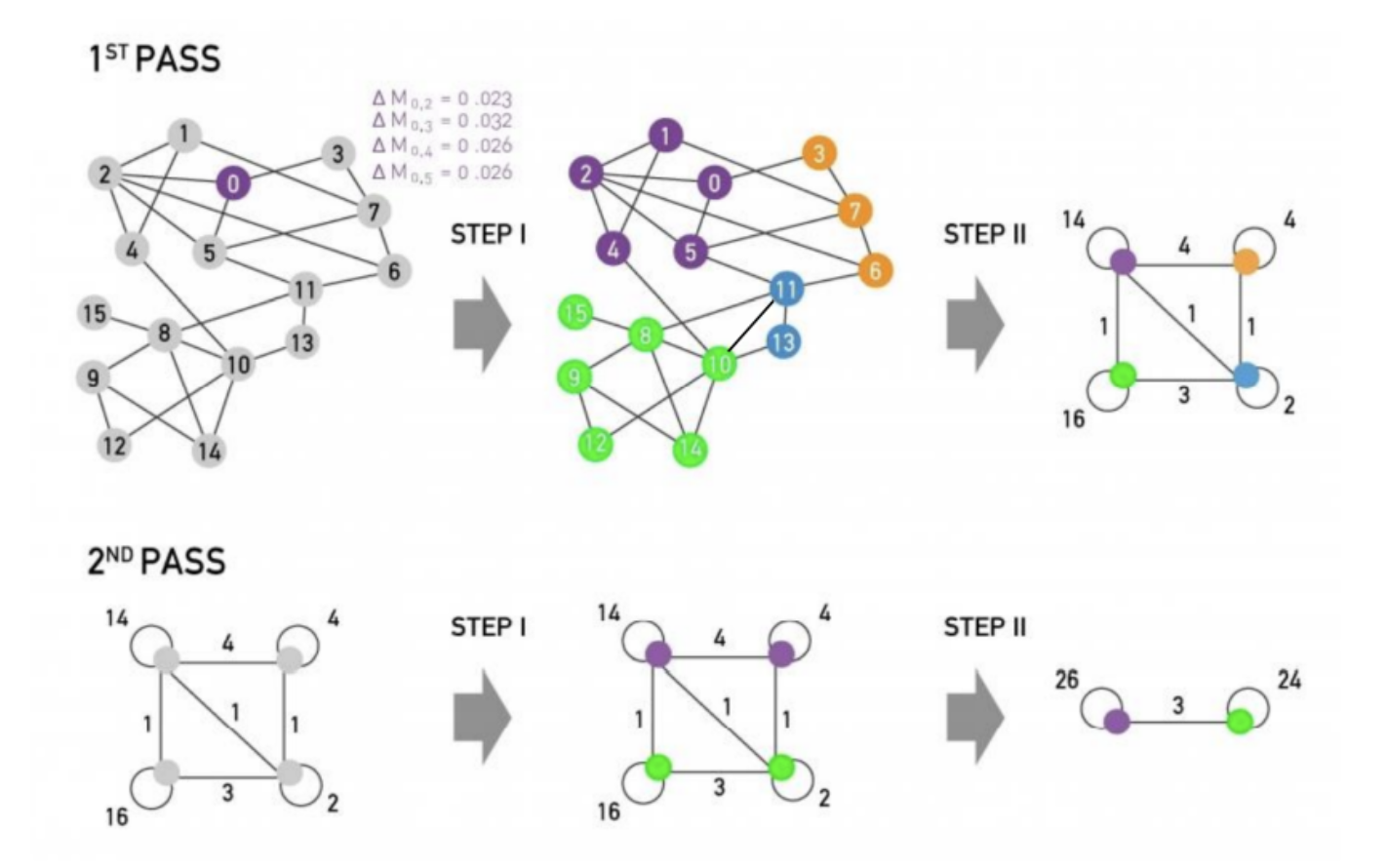
- 같은 community의 노드들을 합쳐 하나의 super node로 표현한다.
- Super node들 사이에 하나의 edge라도 있으면 연결한다.
- 두 super node 간의 edge 가중치는 community 간의 모든 edge 가중치들의 합이다.
- Super graph를 구한 후에는 다시 phase 1으로 돌아가며 한 개의 community가 나올 때까지 반복한다.
- 2개의 communities를 가지는 그래프 -> 4개의 communities를 가지는 그래프와 같은 식으로 hierarchical structure를 만들 수 있다.
4. Detecting Overlapping Communities : BigCLAM
AGM(Community Affiliation Graph Model)

- 실세계에서 사람들은 고등학교 동창이면서 대학교 동창인 것처럼 community가 ovelap 될 수 있다.
- 인접행렬에서도 community가 겹치지 않는다면 위와 같겠지만 여러 community에 속할 수 있다면 아래와 같이 겹치는 부분이 생길 수 있다.
- Overlapping communities는 2가지 step으로 진행된다.
- Node community affiliations에 기반한 그래프 생성모델을 정의한다.(Community Affiliation Graph Model = AGM)
- 그래프 가 주어졌을 때, 를 만드는 최적의 AGM을 찾는다.
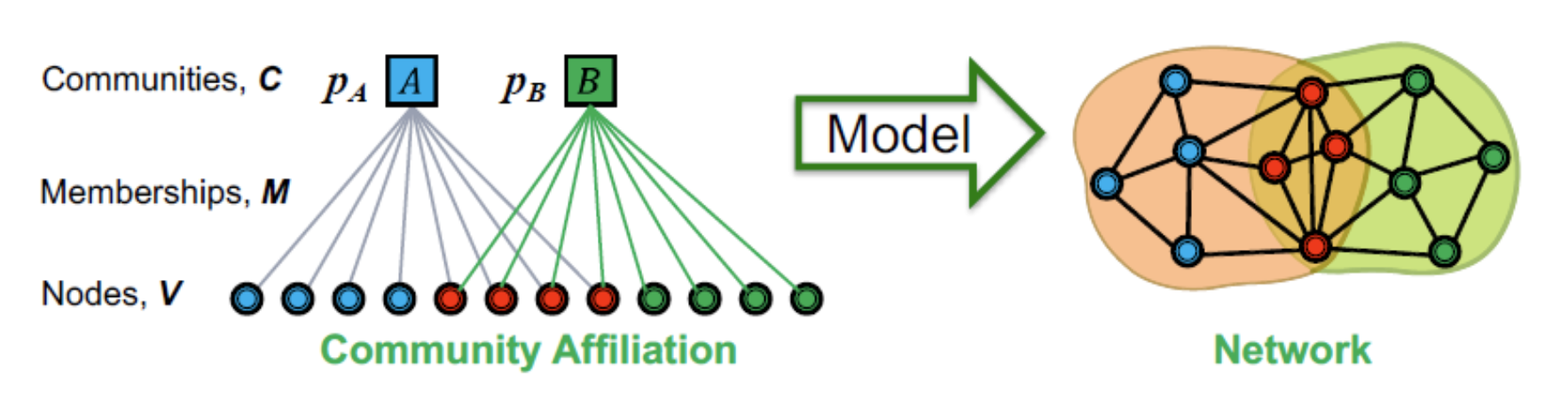
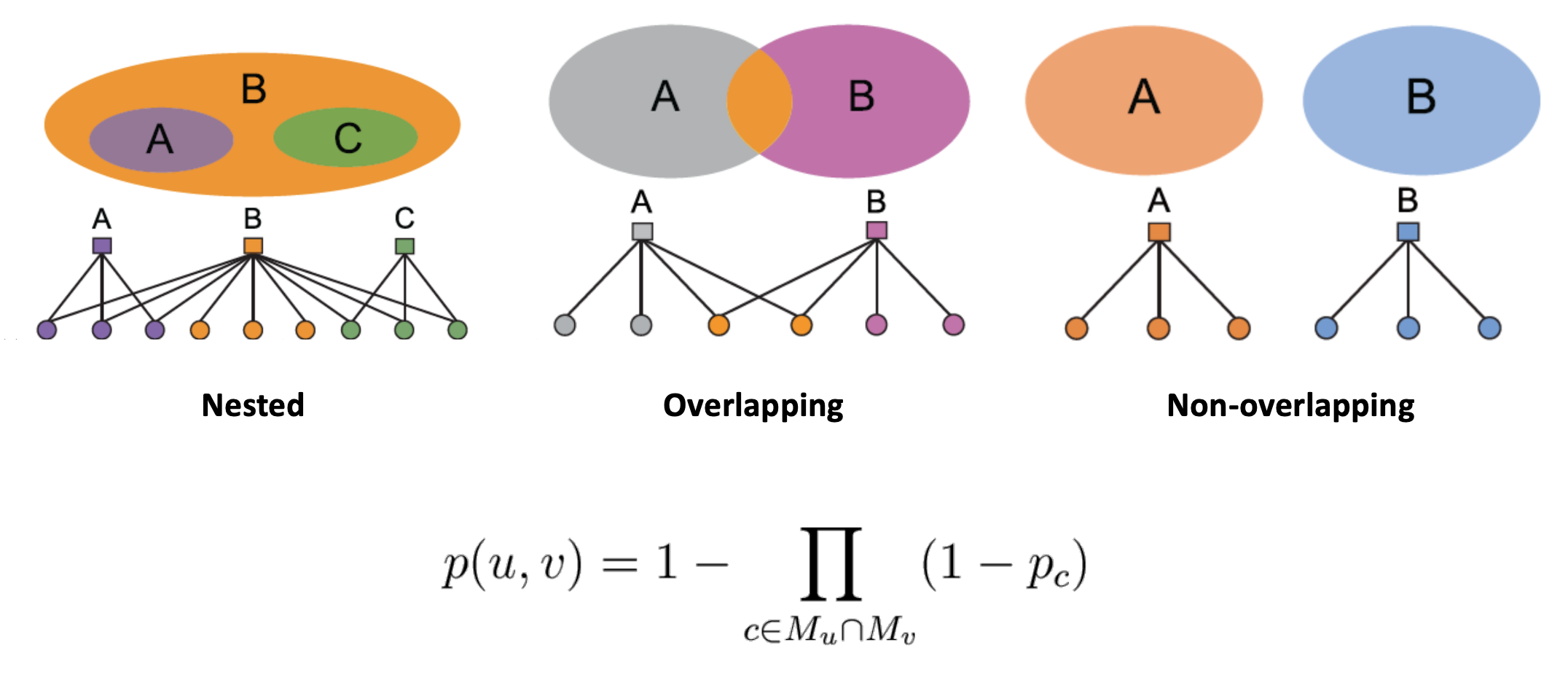
- : 가 서로 연결되어 있을 확률
- 노드 의 공통 communities
- 어떤 노드가 community와 연결될 확률
- 엣지는 위와 같은 식으로 확률값을 구할 수 있다.
- AGM은 다양한 community 구조를 표현할 수 있다.
Detecting Communities
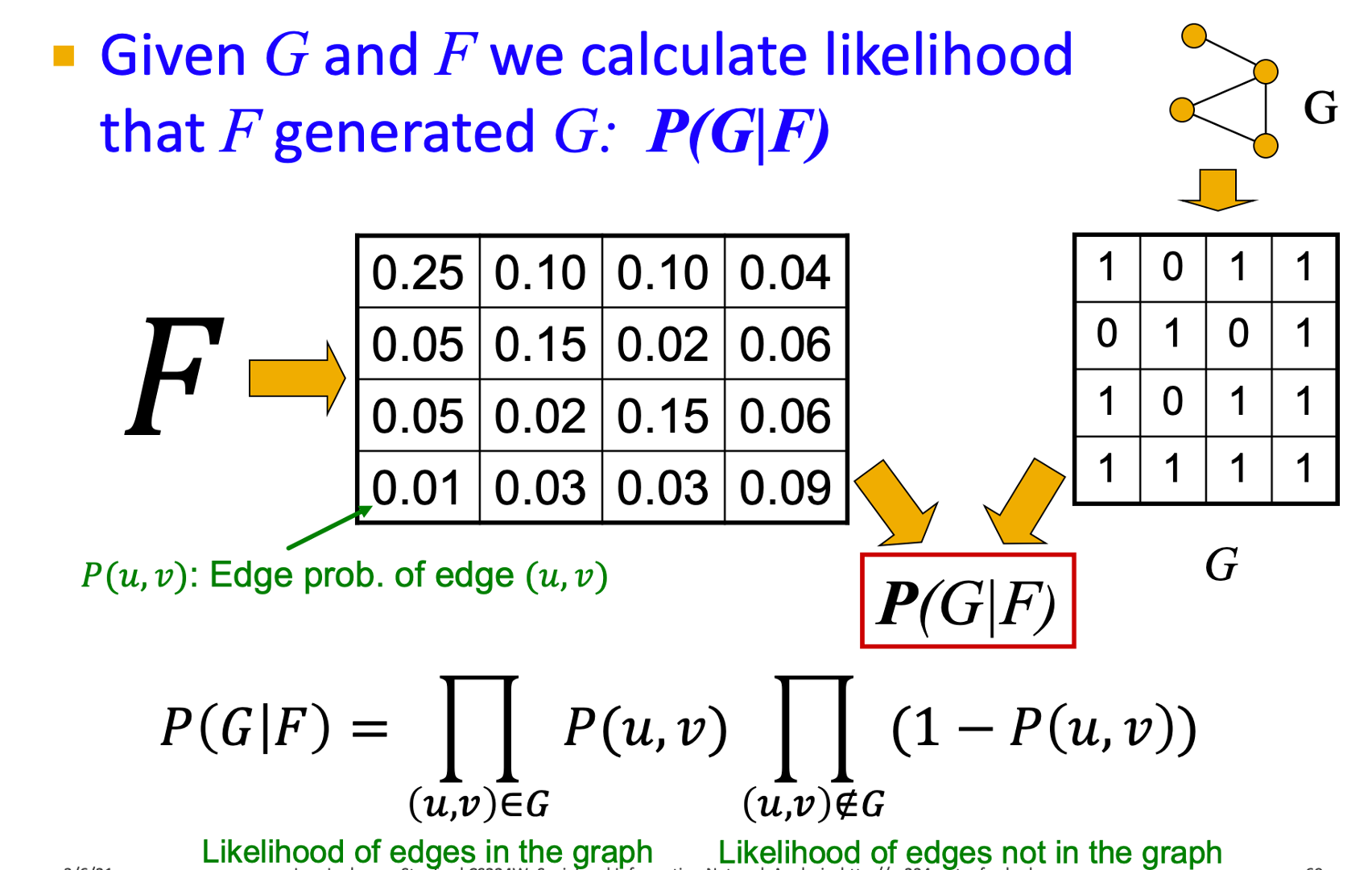
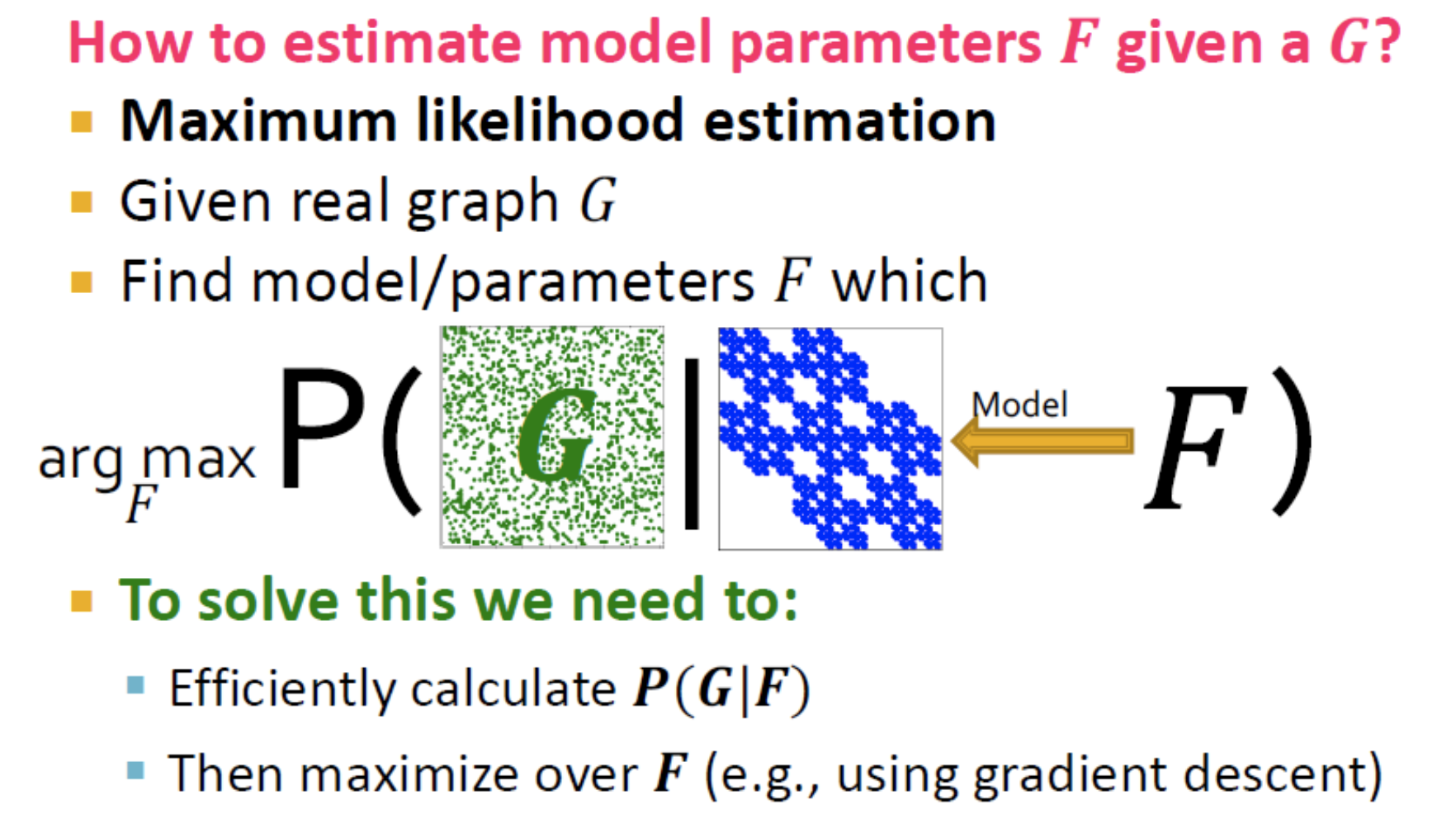
- 그래프 가 주어졌을 때 모델 파라미터 는 MLE를 통해 추정한다.
- 즉, 가 주어졌을 때 가 나올 확률을 최대화하는 를 찾는다.
BigCLAM Model
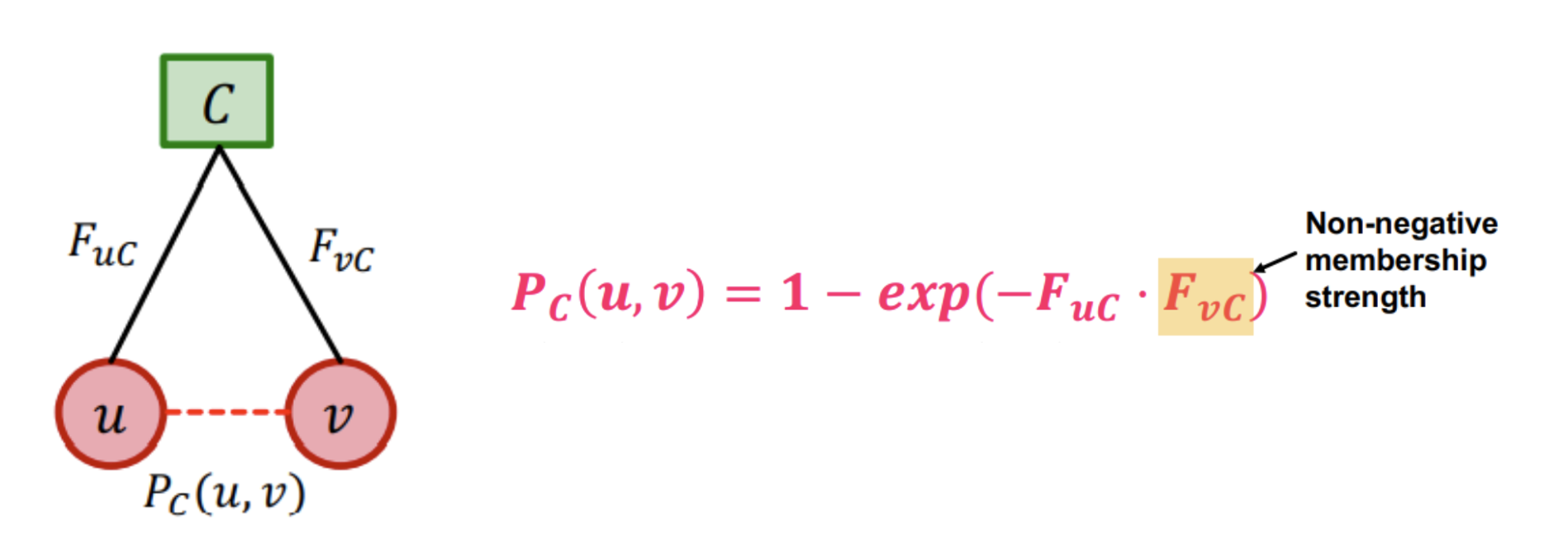
- 위의 모델에서는 노드들이 어떠한 community에 속하는지에 대한 여부만 따졌지만 실제로는 overlapping communities이기 때문에 모든 node community membership의 strength를 구해야 한다.
- 는 community 에 대한 노드 의 strength이며 는 노드 가 community 에 의해 연결될 확률을 의미한다.
- 은 양수이므로 는 0~1 사이의 값을 가진다.
- 노드 가 연결되어 있을 확률은 memberships의 strength에 비례한다.
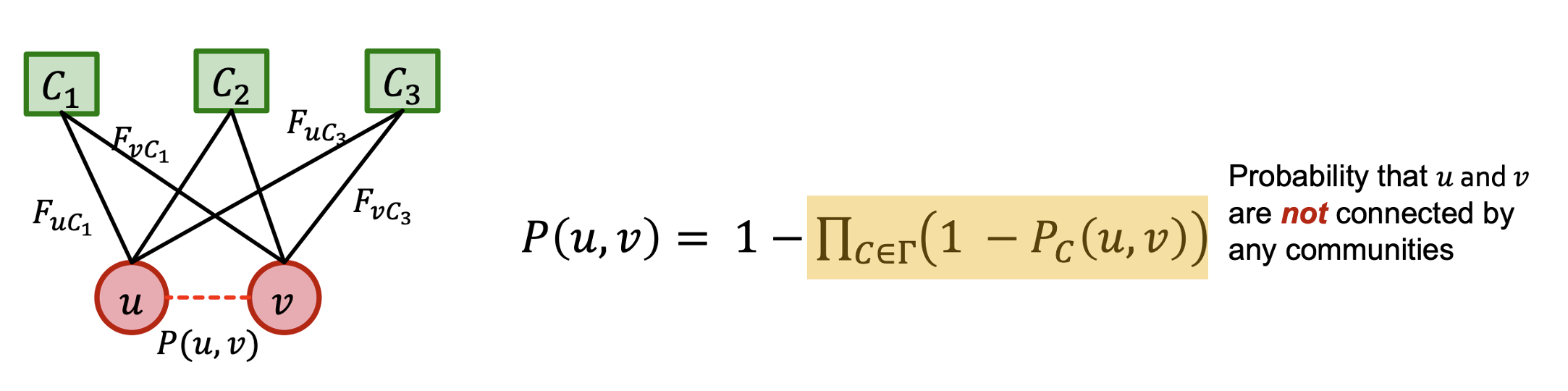
- 노드 는 여러 communities로 연결될 수도 있다.
- 는 모든 communities의 집합을 의미한다.
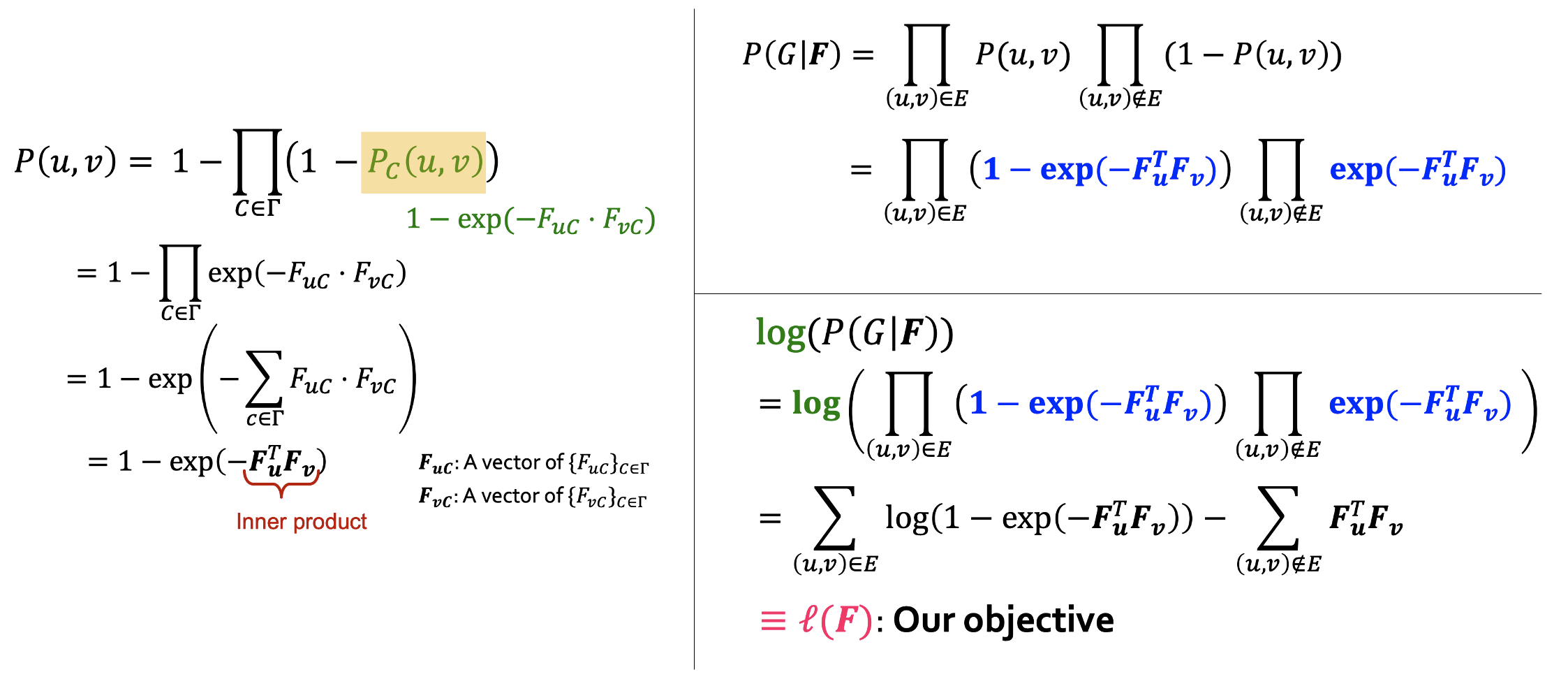
- 를 풀어쓰면 가 되며 에 로그를 취해 strength의 내적에 대한 합 연산으로 objective function을 정의할 수 있다.
References
- Lecture 13.1: https://www.youtube.com/watch?v=KXi4ha79o3s&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=37
- Lecture 13.2: https://www.youtube.com/watch?v=mJQrtXZT5pw&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=38
- Lecture 13.3: https://www.youtube.com/watch?v=0zuiLBOIcsw&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=39
- Lecture 13.4: https://www.youtube.com/watch?v=SHcVHrsgj8w&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=40
