<CS224W> Lecture 11. Reasoning over Knowledge Graphs
1. Reasoning in Knowledge Graphs using Embeddings
Reasoning
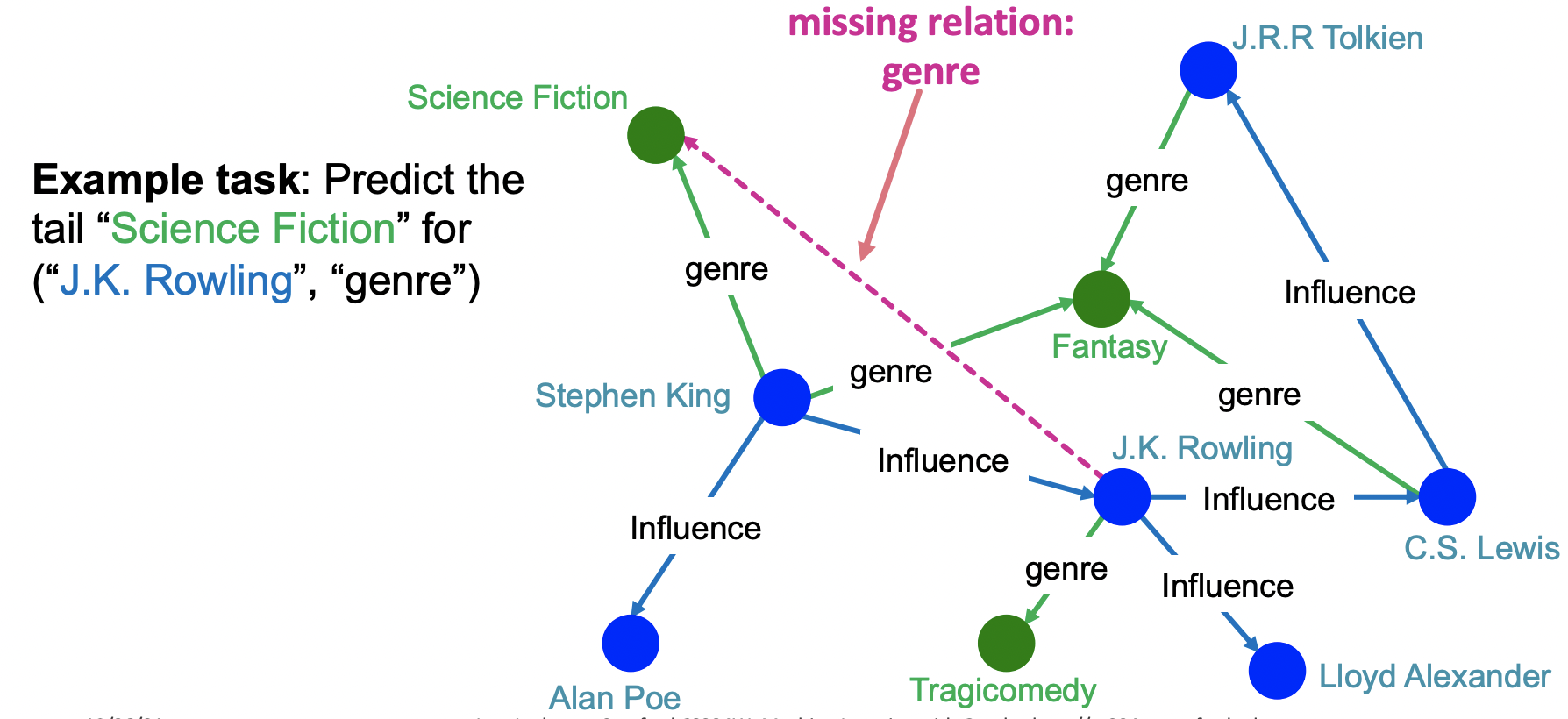
- 이전 lecture에서는 head와 relation이 주어졌을 때 tail을 예측하는 completion task에 대해 보았다.
- 이번 lecture에서 나오는 reasoning은 예측의 범위를 n hop으로 확장하는 task이다.
- Reasoning의 예시로는 One-hop Queries, Path Queries, Conjunctive Queries가 있다.

- One-hop Queries: KG completion과 동일한 task로 head와 relation이 주어졌을 때 tail을 예측한다.
- Path Queries: 출발하는 노드(anchor) va로부터 n개의 관계를 거쳐 도달하는 노드에 대해 예측한다.
q=(va,(r1,...,rn))
- Conjunctive Queries: 다수의 (head, relation) 쌍이 주어졌을 때 공통된 tail을 예측한다.
2. Answering Predicteve Queries on Knowledge Graphs
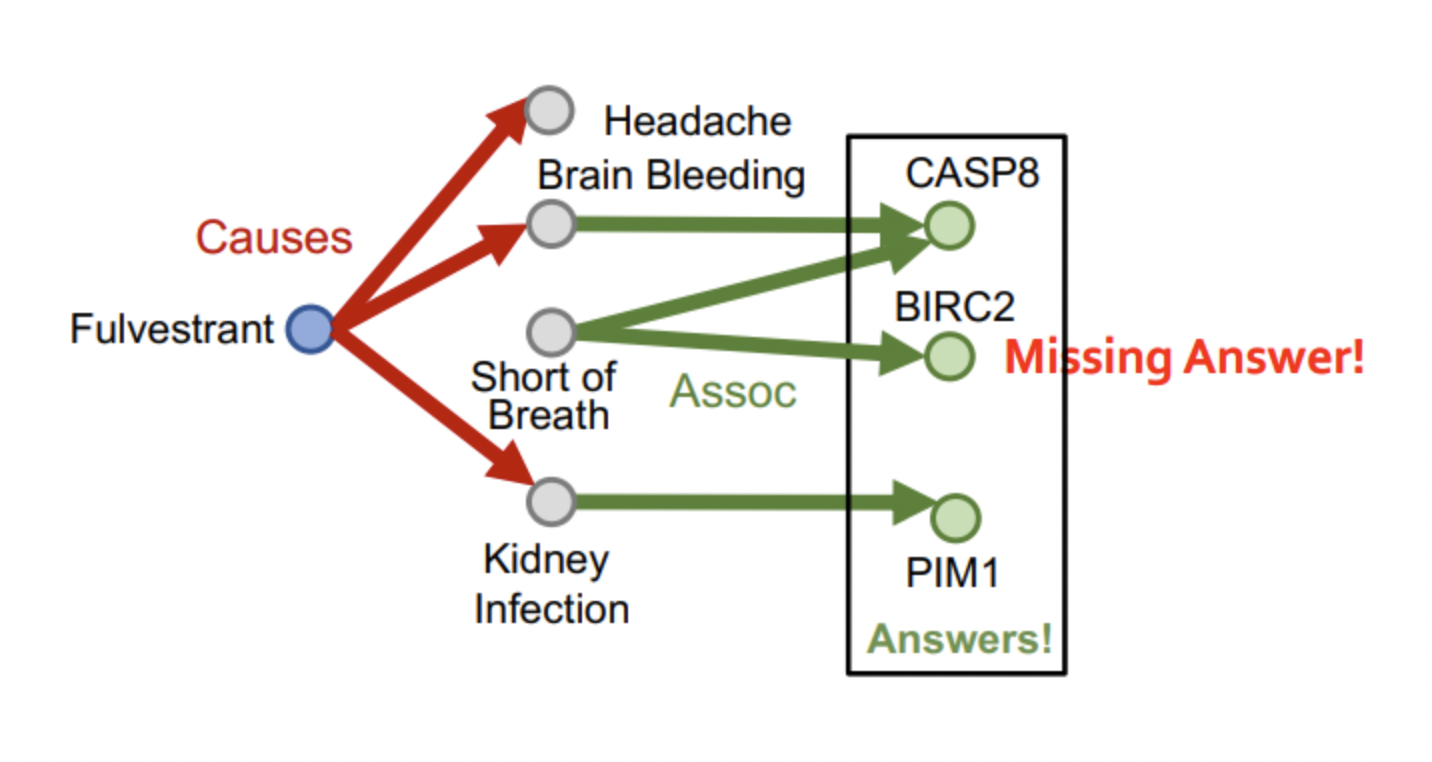
- Path Queries를 위해서는 엣지를 따라가 (va,(r1,...,rn))을 만족하는 노드를 찾으면 되지만 지식 그래프는 불완전한 정보인 경우가 많아 위와 같이 엣지가 빠져있을 경우 정답을 못 찾을 수 있다.
- KG completion을 통해 그래프를 완성시키고 탐색하는 방법이 있지만 Length L에 대해 시간 복잡도가 O(dL)로 너무 크다는 단점이 있다.
- 따라서, 불완전한 그래프 상에서 query에 대해 누락된 정보에 대해 내재적으로 연산하여 정답을 예측하는 predictive queries를 수행한다.
Traversing KG in Vector Space
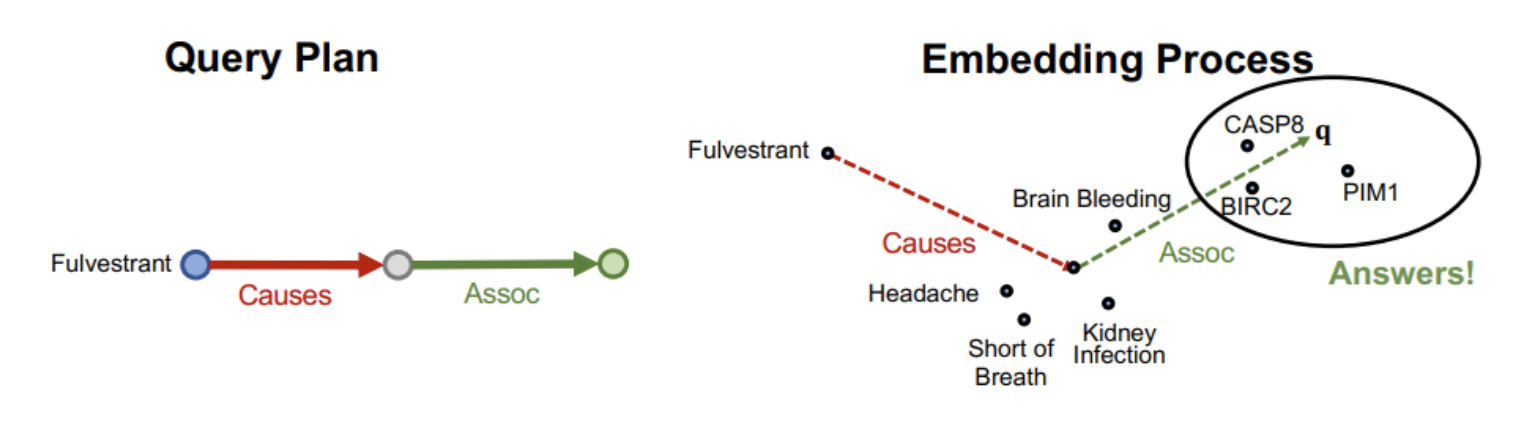
- Lecture10에서 배운 TransE를 활용한다면 임베딩을 통해 합성 관계를 표현할 수 있다.
q=va+r1+⋅⋅⋅rn
- n-hop을 거친 후의 벡터와 가까운 entity 임베딩 벡터를 예측값으로 삼는다.
Conjunctive Queries
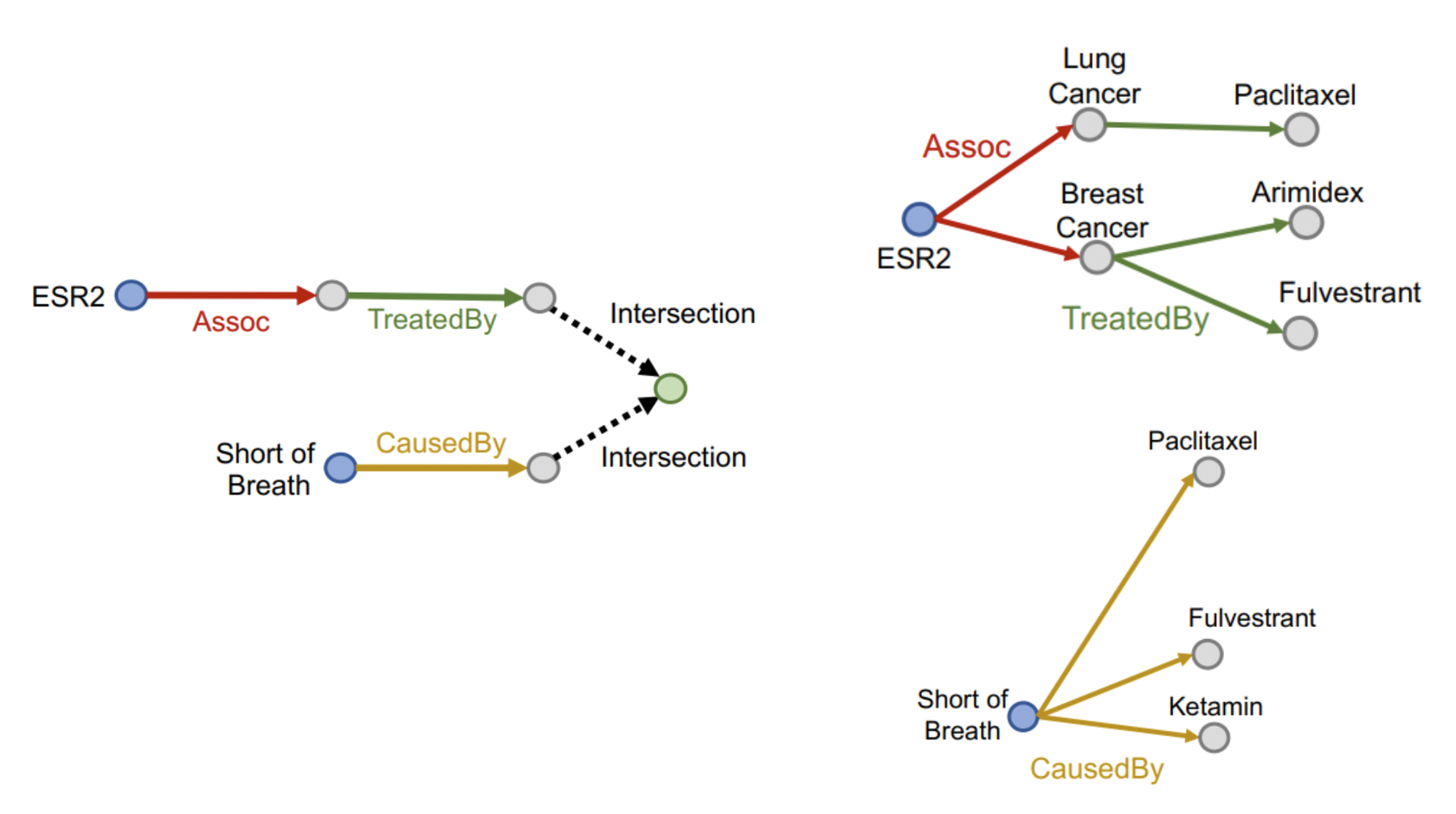
- Conjunctive Queries에서는 anchor가 다수이다.
- ESR2에서 시작하여 예측한 노드들과 Short of Breath에서 시작하여 예측한 노드들의 교집합인 Paclitaxel 혹은 Fulvestrant가 tail로 선택된다.
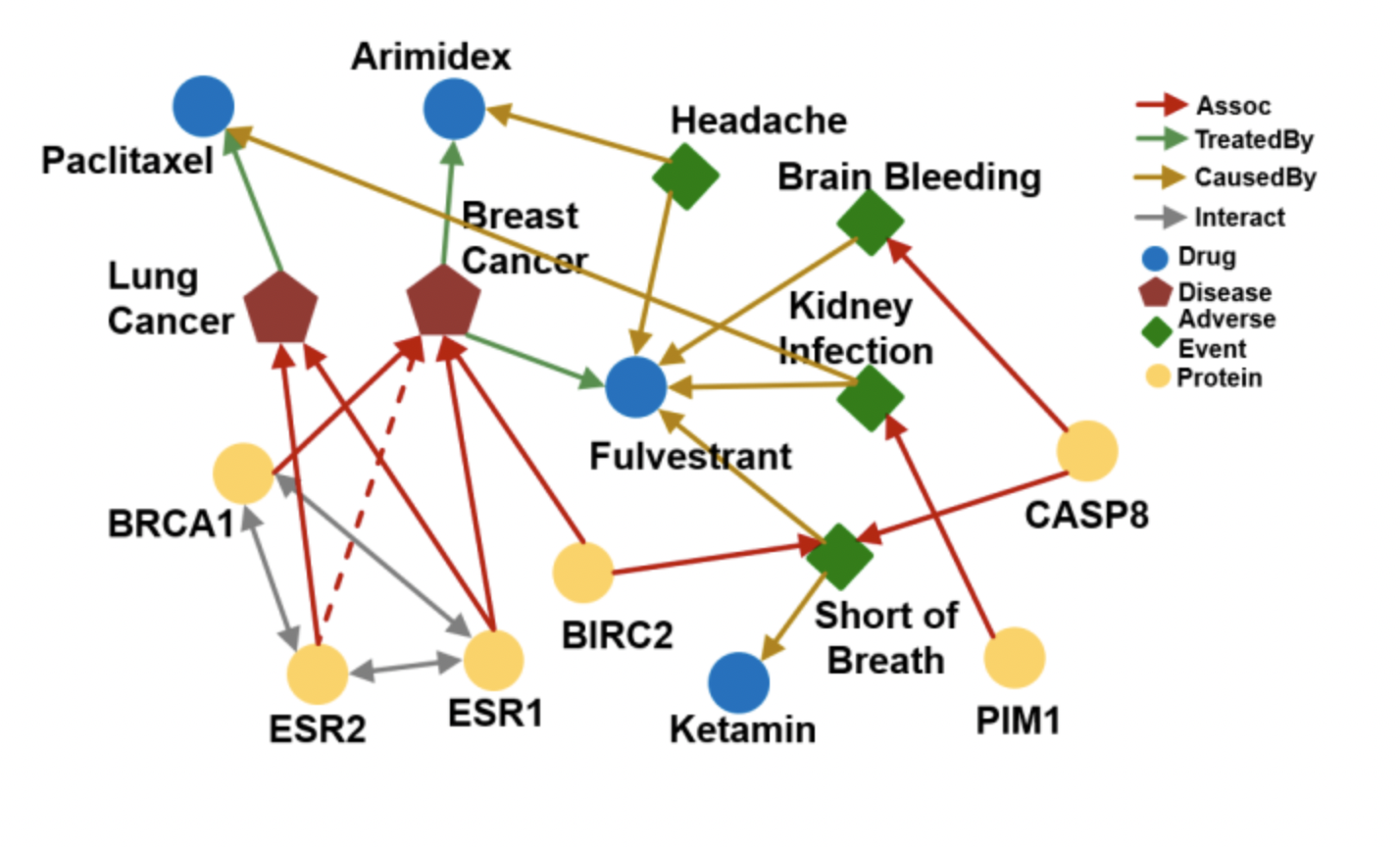
- 하지만, 그래프는 완전하지 않기 때문에 ESR2->Breast Cancer 엣지가 없을 수 있으며 이럴 경우 Fulvestrant는 예측하지 못하게 된다.
- 이 때, Breast Cancer은 BRCA1을 거쳐 ESR2와 연결되어 있기 때문에 둘의 연결관계를 모델이 내재적으로 인지할 수 있어야 한다.
3. Query2Box
Box Embeddings
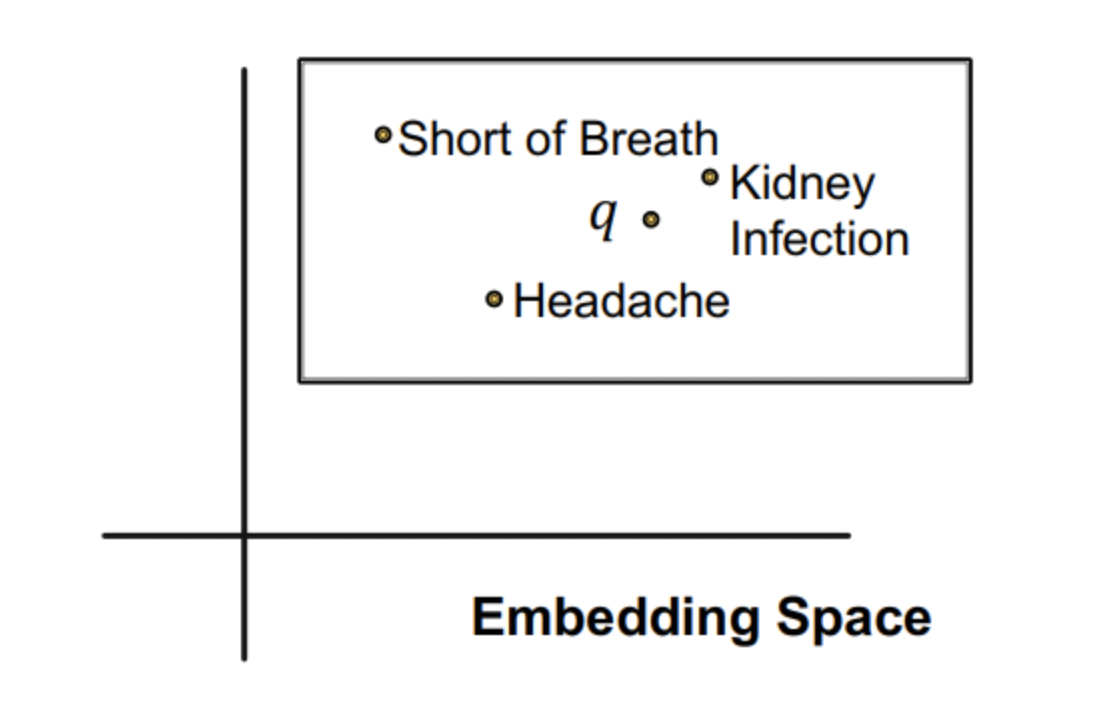
- 임베딩 공간에서 query(entity+relation)는 박스 형태로 표현할 수 있다.
- Query의 tail이 박스 내에 위치하며 q=(Center(q),offset(q))이다.
- 박스를 활용할 경우 Conjunctive queries의 정답을 두 anchor로부터 나오는 예측 tail set들의 교집합으로 쉽게 표현할 수 있다.
- Entity embedding는 크기가 0인 박스로 취급하며 파라미터 수는 d∣V∣이다. d는 out degree, ∣V∣는 entities의 수를 의미한다.
- Relation embedding의 파라미터 수는 2d∣R∣이며 R은 relations의 수를 의미한다.
- f는 두 박스를 받아 교집합 박스를 output으로 내주는 함수이다.
Projection Operator
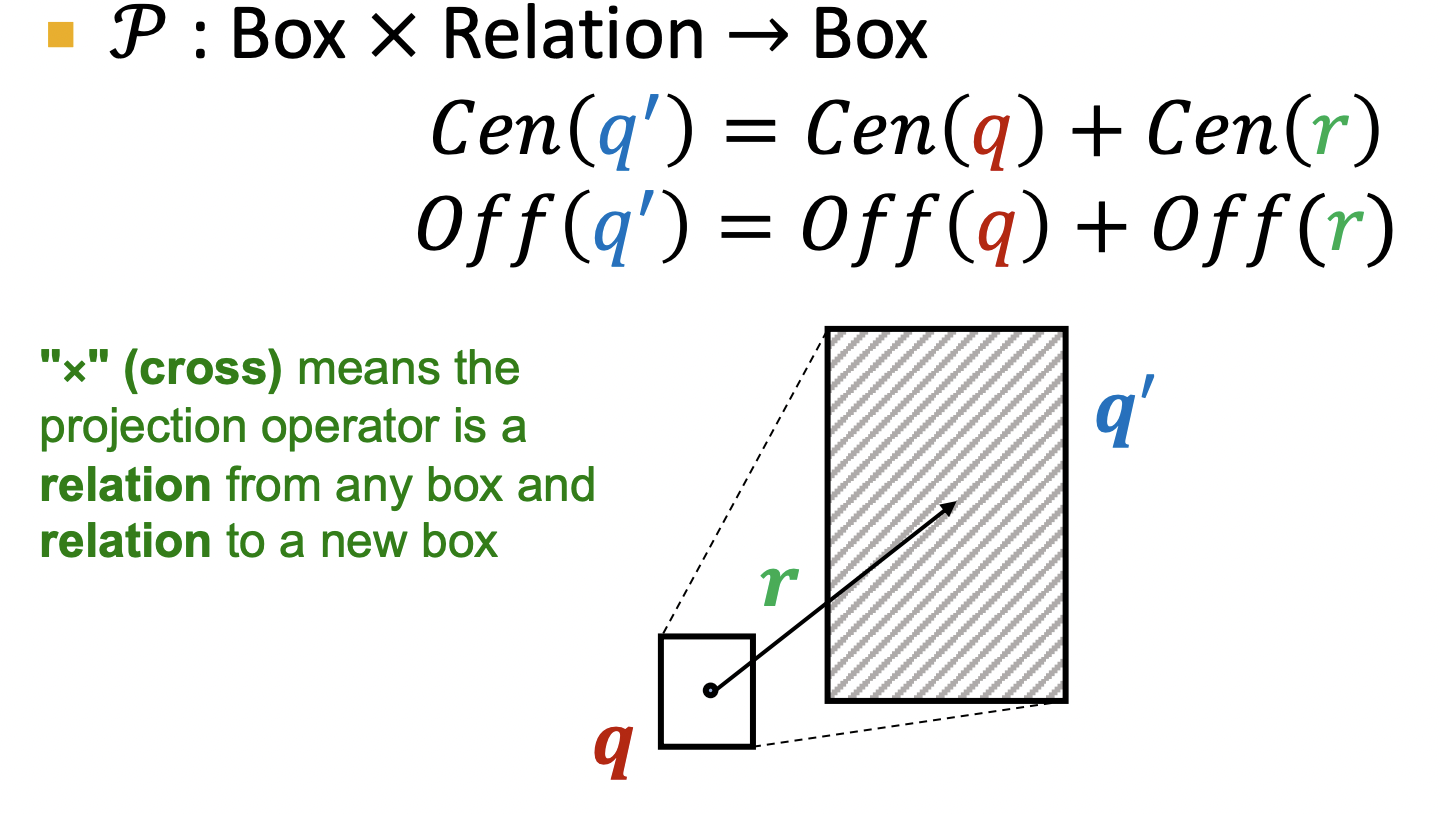
- Projection Operator P는 box와 relation을 입력으로 받아 box의 중심과 크기를 변형시킨다.
- 기존 박스에 대한 벡터 q와 relation 벡터를 선형결합한다.
Embed with Box Embedding
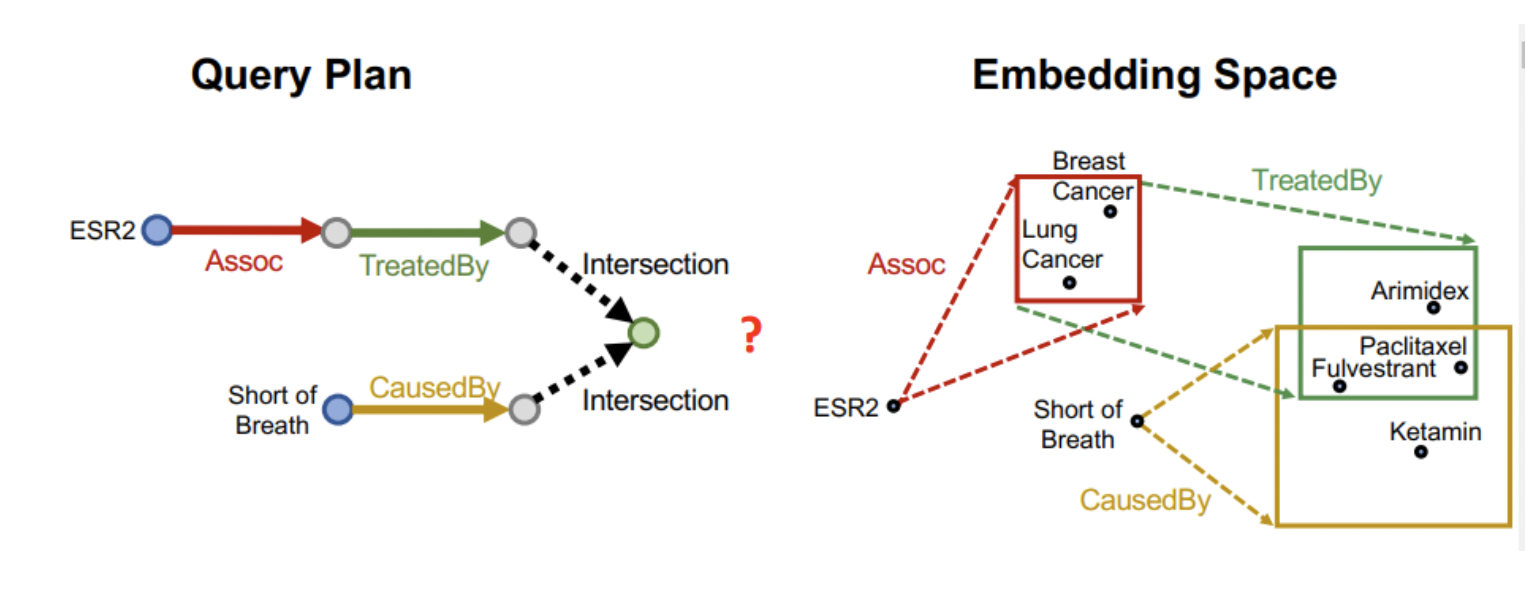
- Anchor 노드의 임베딩 벡터는 크기가 0인 박스로 표현된다.
- q=P(ESR2,Assoc)을 통해 tail에 해당하는 노드 집합을 담는 center와 offset을 갖는 박스 임베딩이 형성된다.
- q′=P(q,TreatedBy)를 통해 새로운 박스 임베딩이 만들어진다.
- 또 다른 anchor인 Short of Breath에서 시작하는 tail에 대한 박스 임베딩도
q=P(ShortofBreath,CausedBy)를 통해 만들어준다.
- 최종적으로 만들어진 초록 박스와 노랑 박스의 교집합을 구한다.
Intersection Operator
Center

- 교집합 박스의 중심은 input 박스들의 중심들과 가까워야 한다.
- 각 박스의 벡터를 함수 fcen을 통과한 후 softmax를 취해 가중치 벡터 wi를 구한다.
- wi와 Cen(qi)를 elment-wise product한 후 summation하여 교집합 박스의 중심을 구한다.
Offset

- 교집합 박스의 크기는 input 박스들보다 작아야 한다.
- Input 박스들의 offset 중 가장 작은 값과 input 박스들을 함수 foff와 시그모이드에 통과시킨 값을 element-wise product하여 교집합 박스의 offset을 구한다.
Entity-to-Box Distance
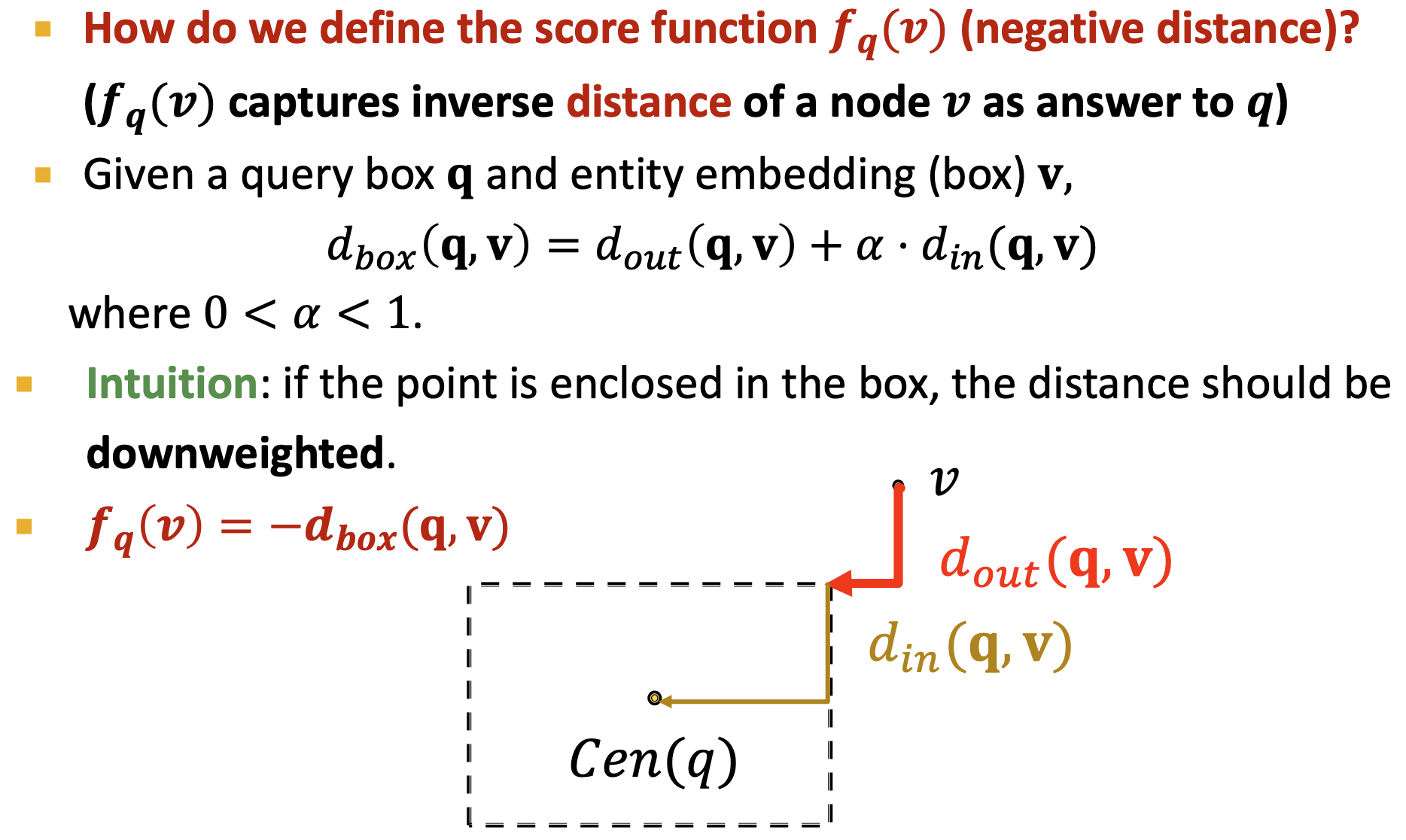
- Score function으로는 negative distance fq(v)를 사용한다.
- 박스 내의 노드에 대해서는 downweight를 적용한다.
And-OR Query
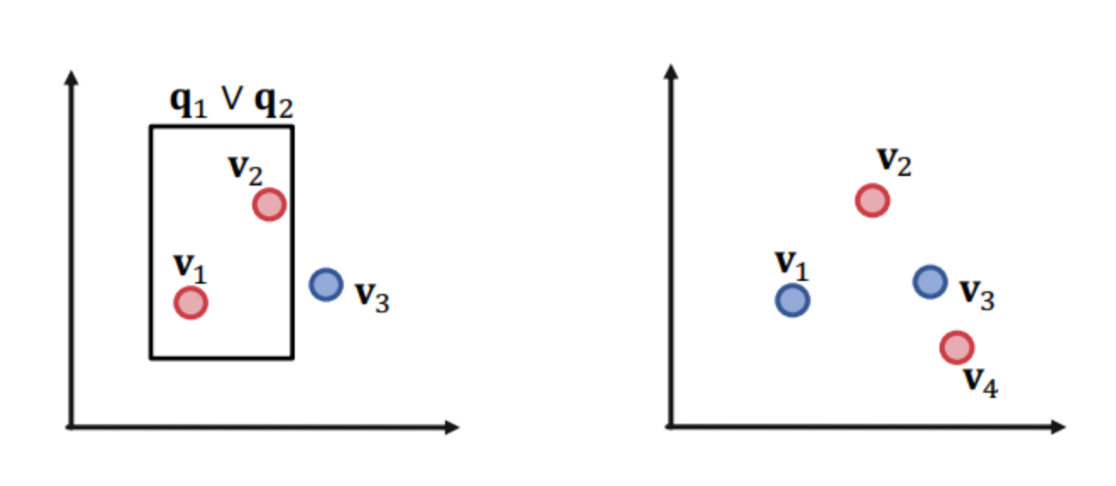
- 임베딩 공간에서 or 연산을 하는 것에는 한계가 있다.
- 2차원에서 query가 3개일 때 or 연산은 가능하지만 4개가 되는 순간 v3를 포함하지 않으면서 v2,v4를 모두 포함하는 박스를 만들수가 없다.
- 즉, m개의 query에 대해 수행하기 위해서는 m+1차원의 공간이 필요하나 그래프에서 노드의 개수는 굉장히 많기 때문에 현실적으로 임베딩 차원을 그렇게까지 늘릴 수는 없다.
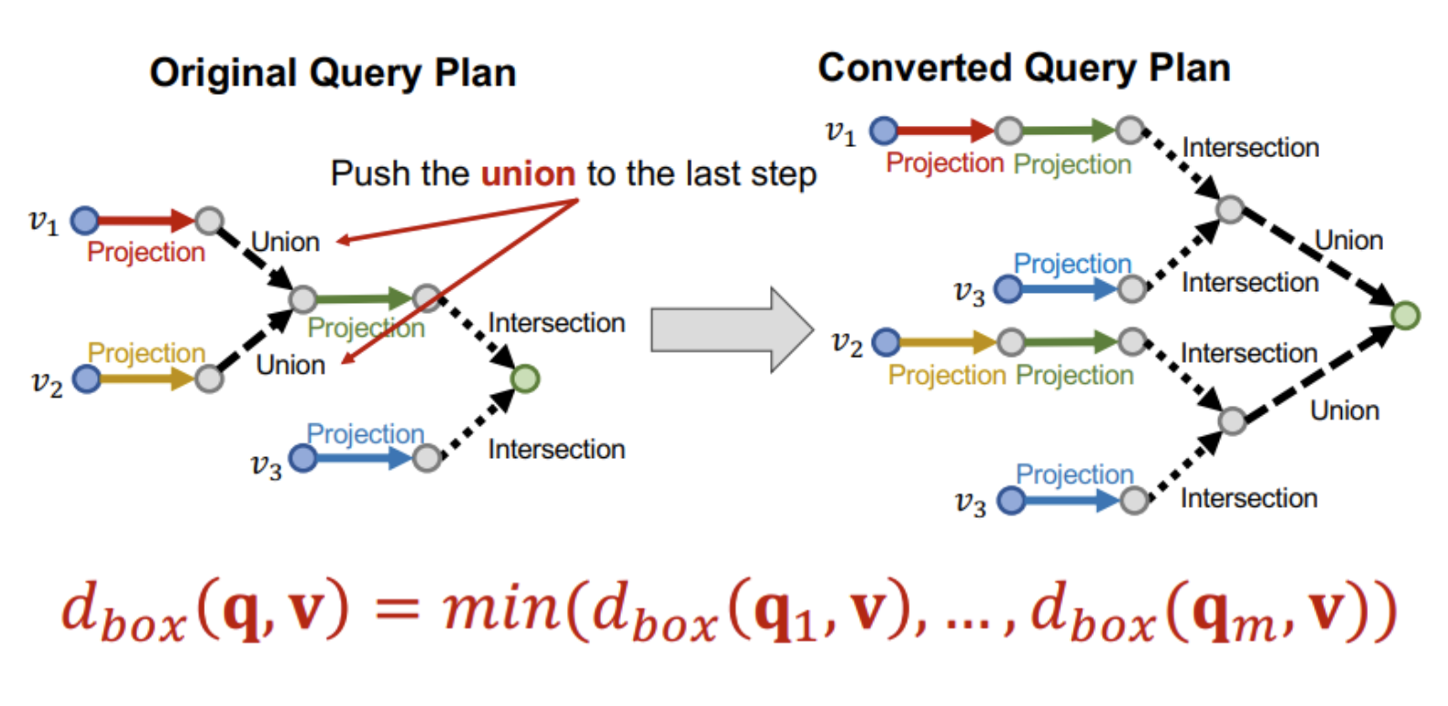
- Or과 and 연산이 함께 있는 경우에는 and 연산을 우선으로 하여 해결할 수 있다.
- 즉, (a∪b)∩c=(a∩c)∪(a∩b)로 변형시켜 활용한다.
- Or 연산은 제일 마지막으로 미뤄놓고 실제로는 수행하지 않는데 q1∨⋅⋅⋅∨qm에서 각 query와 노드 v의 거리 중 최소 거리를 연산하면 되기 때문이다.
4. How to Train Query2box
- 학습시킬 그래프 Gtrain으로부터 query q와 정답 노드 v, 오답 노드v′를 샘플링한다.
- q를 임베딩하여 최종 박스를 구한다.
- 정답 노드와 오답 노드에 대한 스코어 fq(v),fq(v′)를 구한다.
- fq(v)는 최대화하고 fq(v′)는 최소화한다.
l=−logσ(fq(v))−log(1−σ(fq(v′))
- 이 때 샘플링할 query는 편향되지 않도록 모든 노드를 정답으로 하도록 구성해야 한다.
- 따라서 query는 answer 노드를 고른 후 역으로 거슬러 올라가 구성한다.
References














