<CS224W> Lecture 14. Traditional Generative Models for Graphs
1. Properties of Real-world Graphs
Degree Distribution
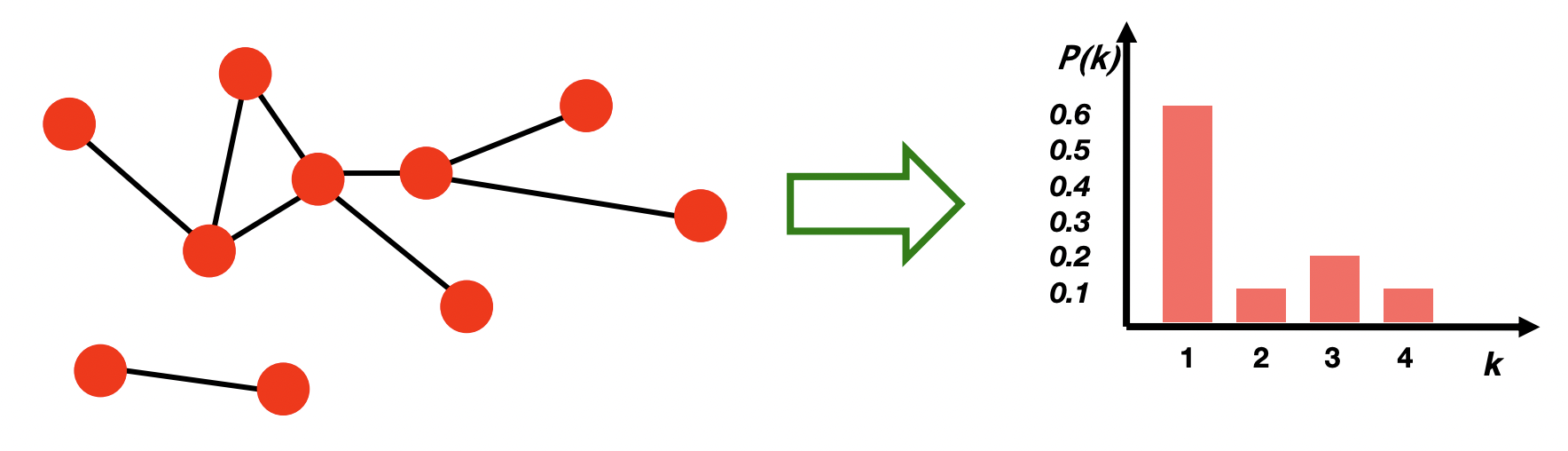
- P(k)로 나타내며 임의로 선택한 노드가 k의 degree를 가질 확률을 의미한다.
- Nk를 degree가 k인 노드의 수라 할 때 정규화된 히스토그램은 P(k)=Nk/N으로 나타낼 수 있다.
Clustering Coefficient
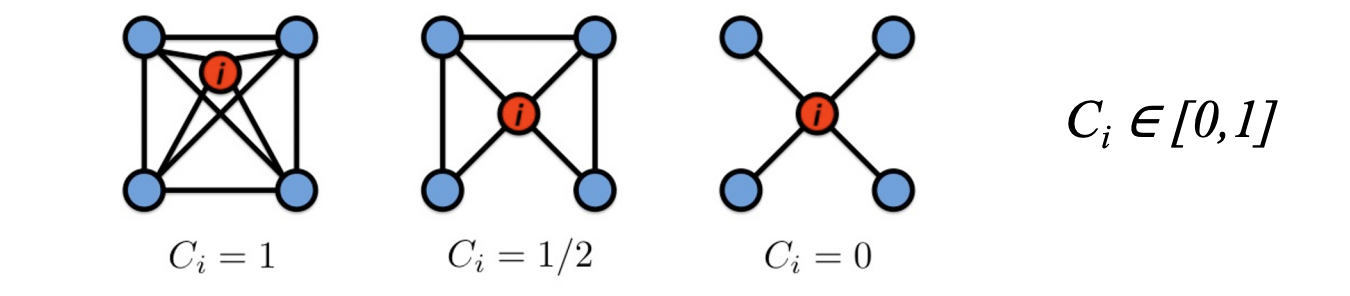
- C로 표기하며 노드 i가 이웃들과 어떻게 연결되어 있는지를 나타낸다.
- Degree가 ki인 노드 i에 대해 Ci=ki(ki−1)2ei
- ei는 노드 i의 이웃 노드들 간의 엣지의 수를 의미한다.
- C=N1∑iNCi. 모든 노드에 대한 평균값으로 C를 정의한다.
Connectivity
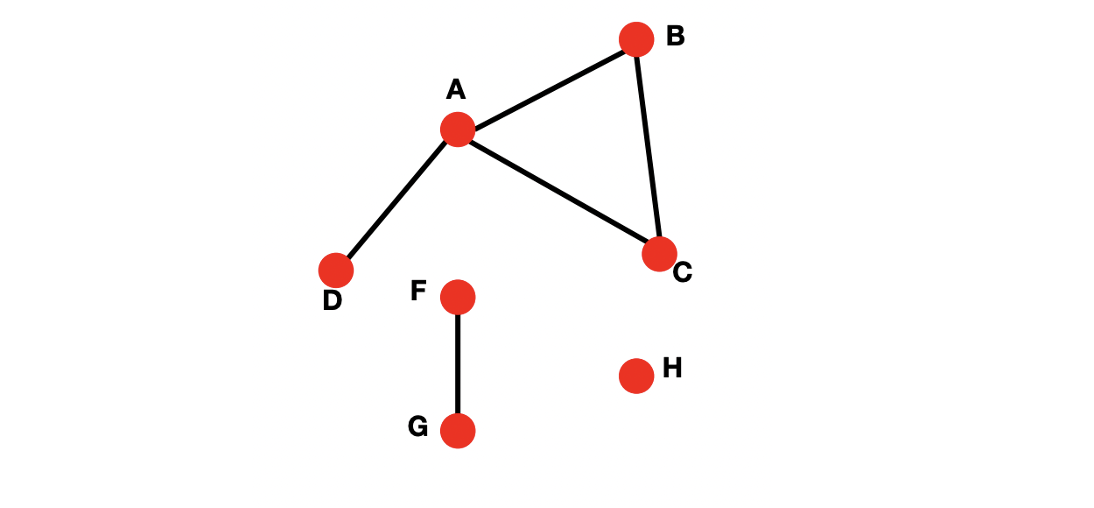
- s로 표기하며 가장 큰 component의 크기를 나타낸다.
- 예를 들어, 99%의 노드들이 연결되어 있으면 s는 매우 크며 giant component라고도 부른다.
- 임의의 노드로부터 출발하며 BFS를 통해 방문한 노드를 표시한다.
- 모든 노드를 방문하면 network는 연결되어 있음을 의미하며 방문하지 않은 노드를 찾으면 BFS를 반복한다.
Path Length
- 최단경로 기준 그래프 내 노드 쌍의 최대 거리를 diameter라 한다.
- 평균 path length는 무한한 길이의 경로를 무시하기 위해 connected grpah에 대해서만 계산한다.
- hˉ=2Emax1∑i,j=ihij
- hij는 노드 i와 j의 거리를, Emax는 엣지의 최대 개수(노드 쌍의 개수)를 의미한다.
Case Study

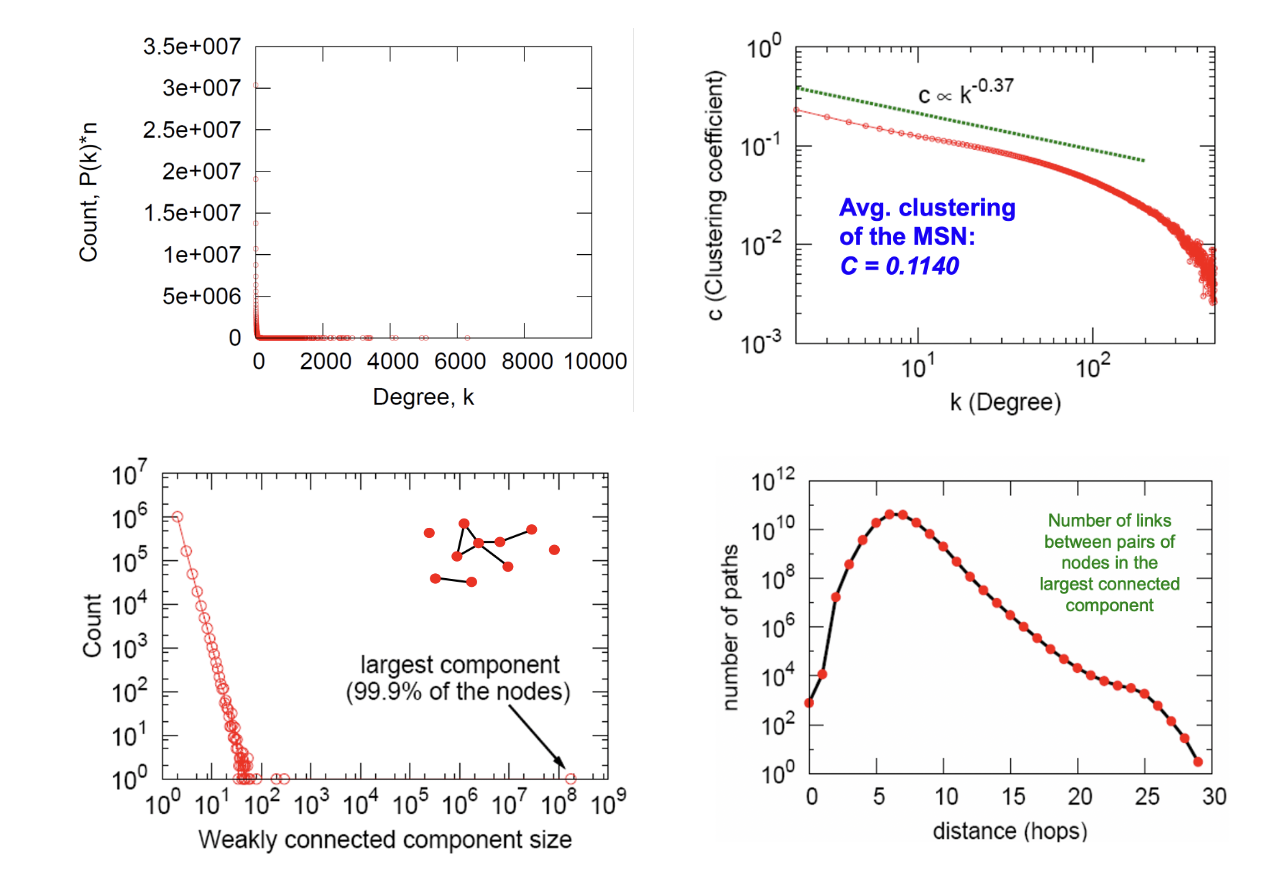
- 메신저 내에서 유저들의 한 달 간 활동내역에 대해 그래프로 나타낼 수 있다.
- Properties에 대한 정보를 얻을 수 있으며 이 값들이 exptected냐 surprising냐에 대해 알기 위해 모델이 필요하다.
2. Erdos-Renyi Random Graphs
- Gnp: 엣지가 독립 항등 분포(iid)의 확률 p를 가지는 노드 n에 대한 undirected graph
- Gnm: m개의 엣지가 균등한 확률로 랜덤하게 뽑히는 노드 n에 대한 undirected graph
- 우리는 Gnp에 대해서만 다룬다.
Properties of Gnp
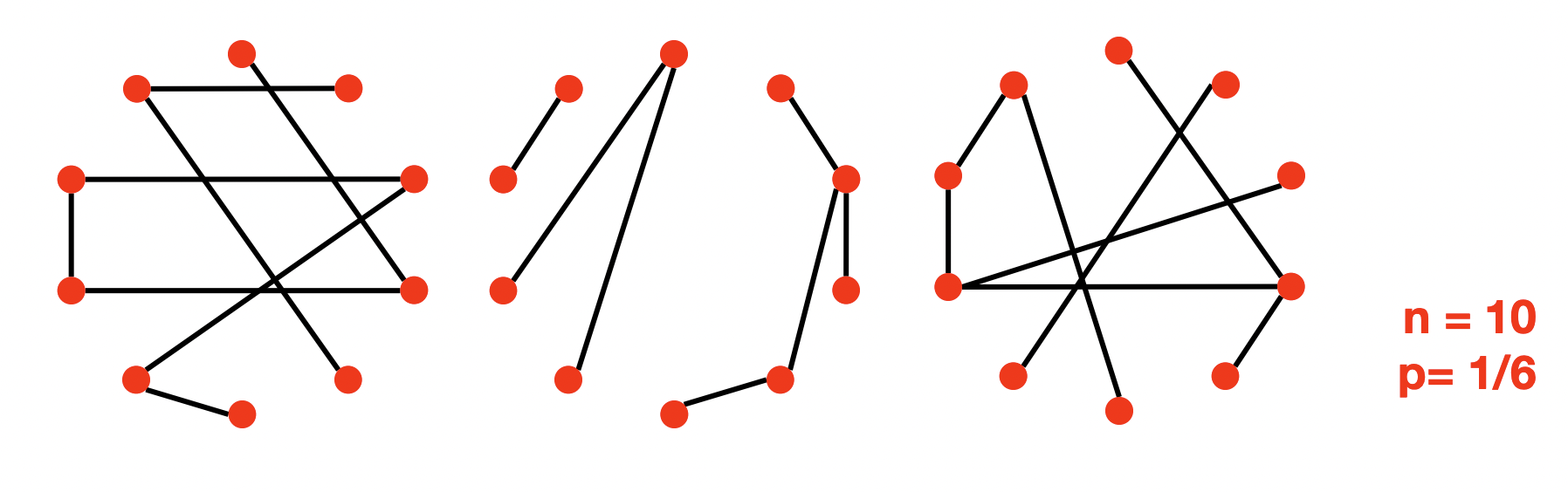
- n,p에 의해 그래프가 unique하게 결정되지 않는다.
- Gnp는 properties로 degree distribution P(k), clustering coefficient C, path length h를 가진다.
Degree Distribution
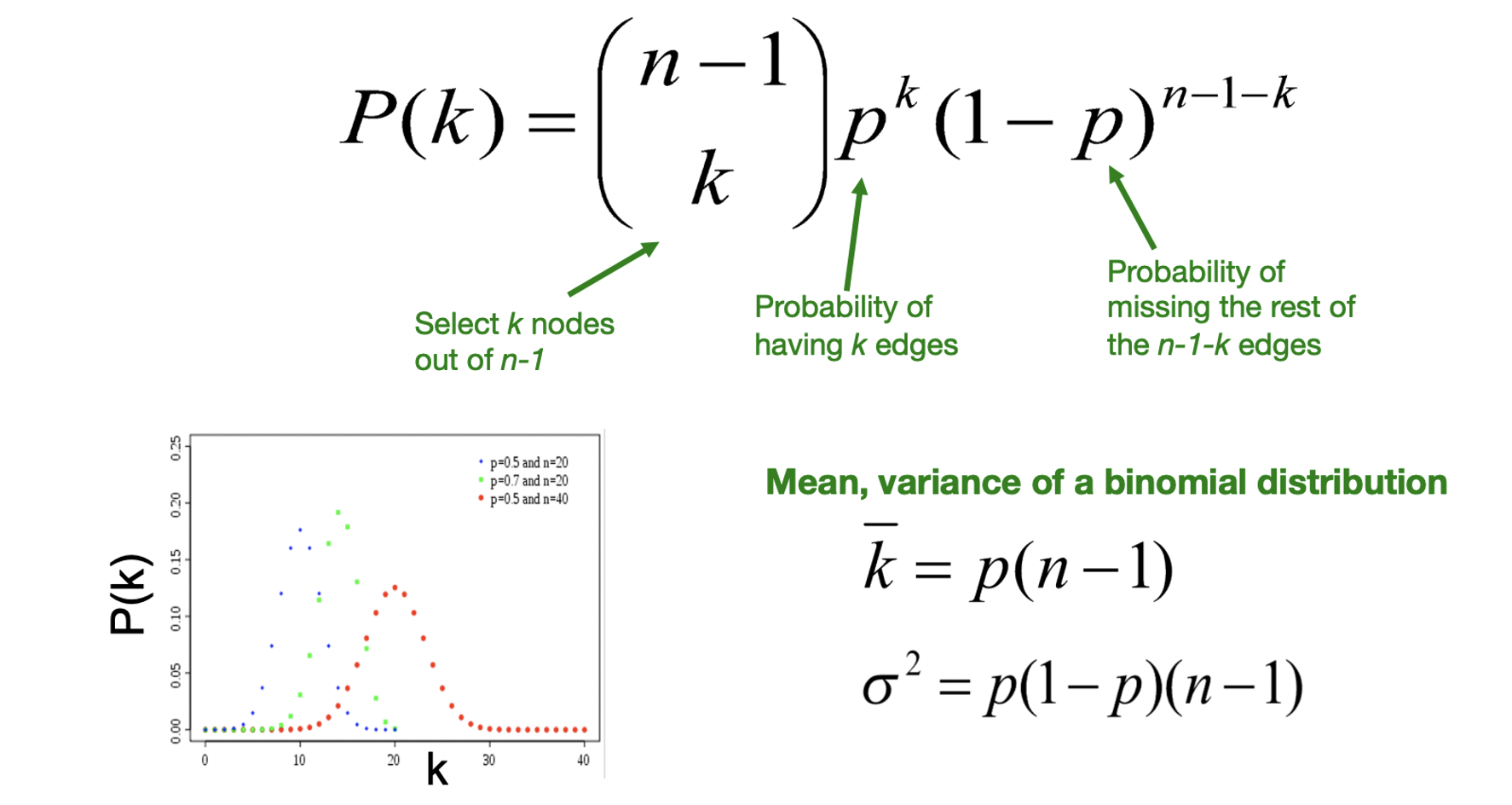
- Gnp의 P(k)는 이항분포를 따른다.
- n−1개 중 선택한 k개는 엣지로 연결되고 나머지는 연결되지 않을 확률이 P(k)가 된다.
Clustering Coefficient
- Ci=ki(ki−1)2ei
- Gnp의 엣지는 p의 확률로 나타나므로 이웃 노드들 간의 엣지의 수의 기댓값 E[ei]는 p2ki(ki−1)가 된다.
- 따라서, E[Ci]==ki(ki−1)p⋅ki(ki−1)=p=n−1kˉ≈nkˉ
Connected Components
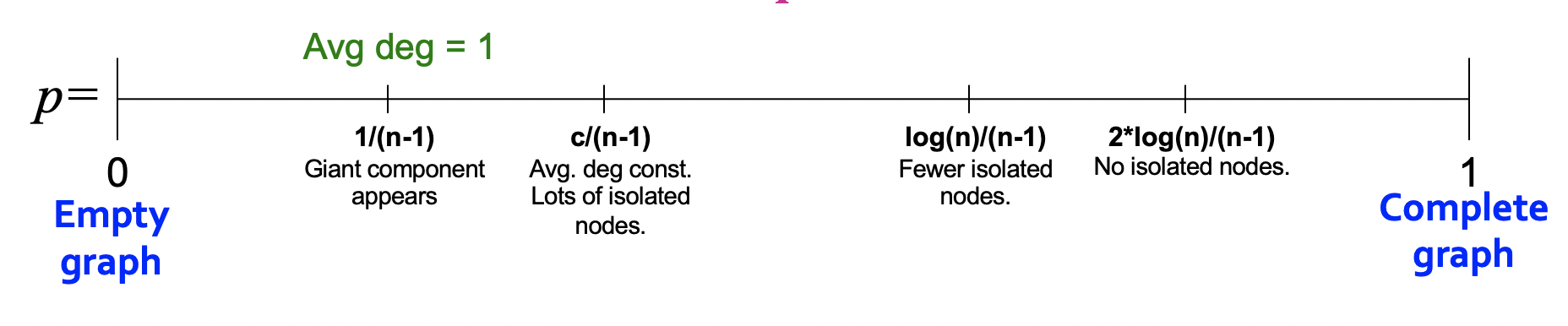
- p=k/(n−1), average degree k=2E/n으로 k=1일 때부터 giant component가 나타난다.
- Degree k=1−ϵ: 모든 components의 크기는 Ω(logn)
- Degree k=1+ϵ: 하나의 component 크기는 Ω(n), 나머지는 Ω(logn)
Expansion
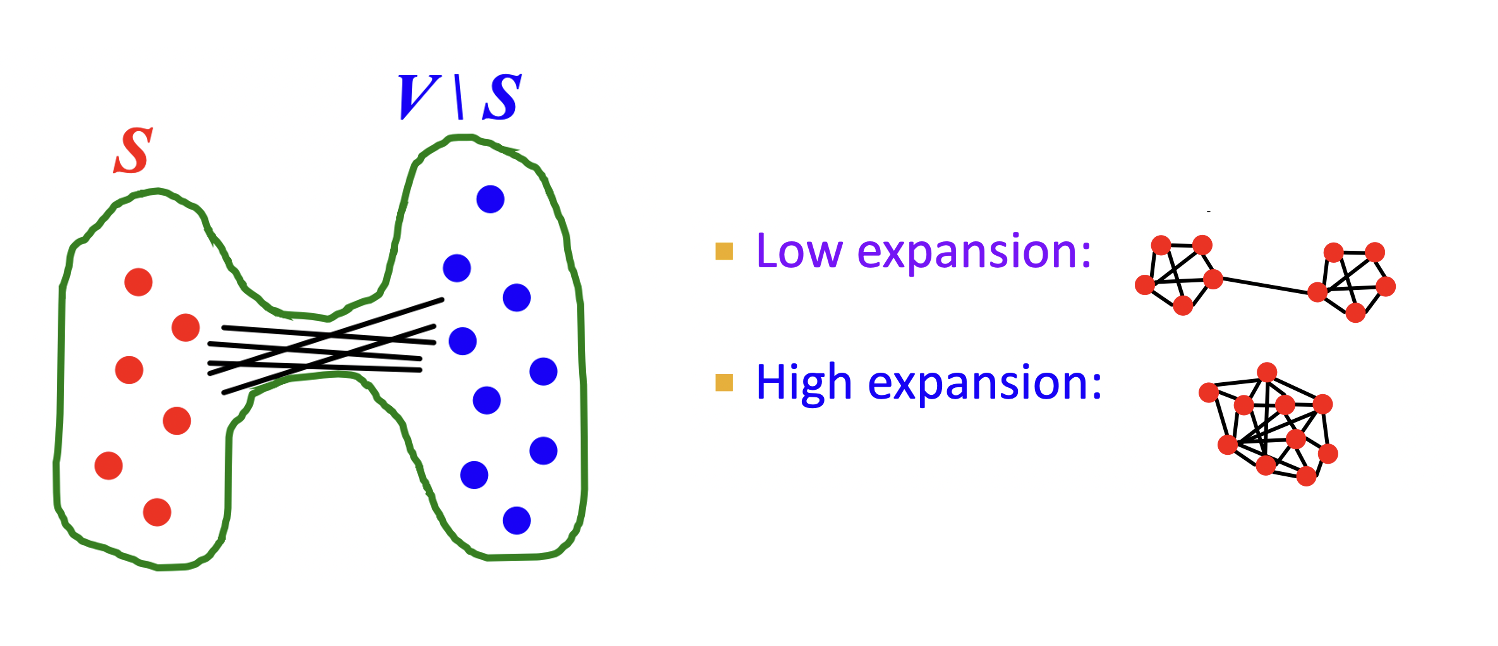
- α=minS⊆Vmin(∣S∣,∣V\S∣)# edges leaving S
- 그래프 G(V,E)에 대해 V의 subset S를 만들기 위해 끊어주어야 하는 엣지의 비율(?)이라고 이해했다.
- 분자인 #edges leaving S는 끊어주는 엣지의 수, V∣S는 S를 뺀 나머지 subset을 의미한다.
- Expansion은 robustness의 척도가 되며 subset을 쉽게 만들 수 있는 구조면 low expansion을, 어려운 구조면 high expansion을 가진다.
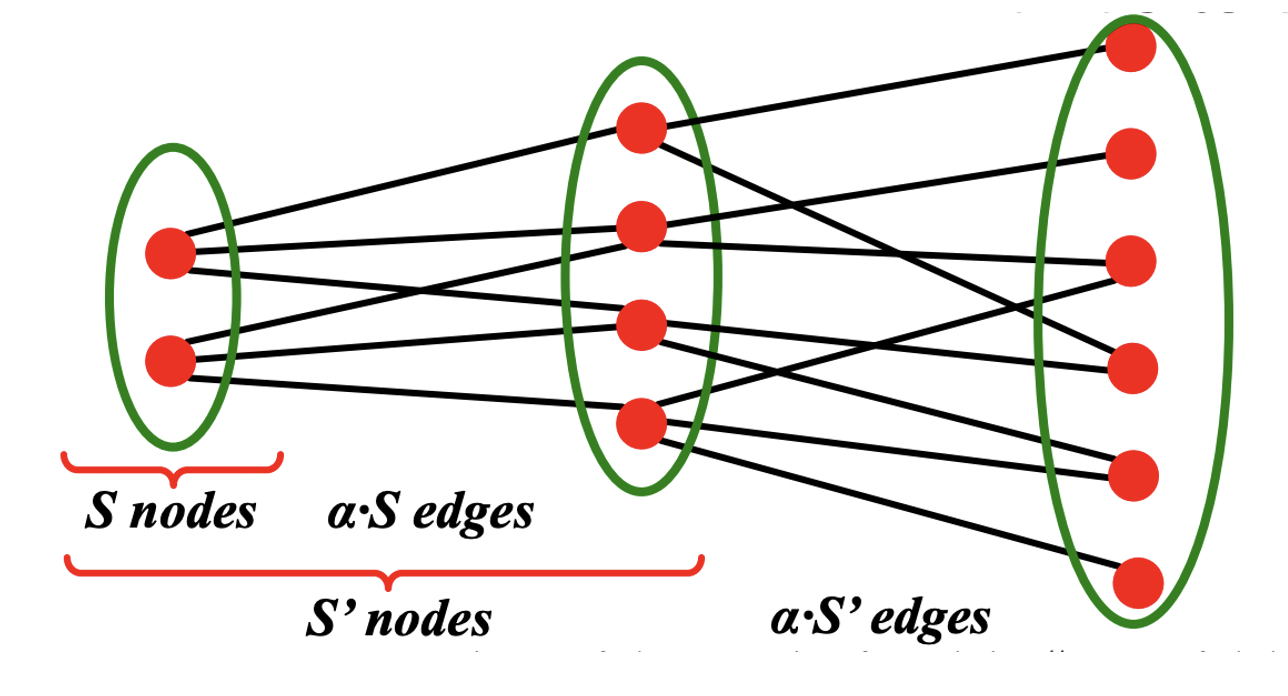
- Expansion이 α이고 n개의 노드를 가지는 그래프의 모든 노드 쌍에 대한 path of length는 O((logn)/α)이다.
- 즉, path length는 노드의 개수에 비례하고 expansion에 반비례한다.
- 랜덤 그래프는 expansion이 커 logn의 BFS로 모든 노드를 방문할 수 있다.
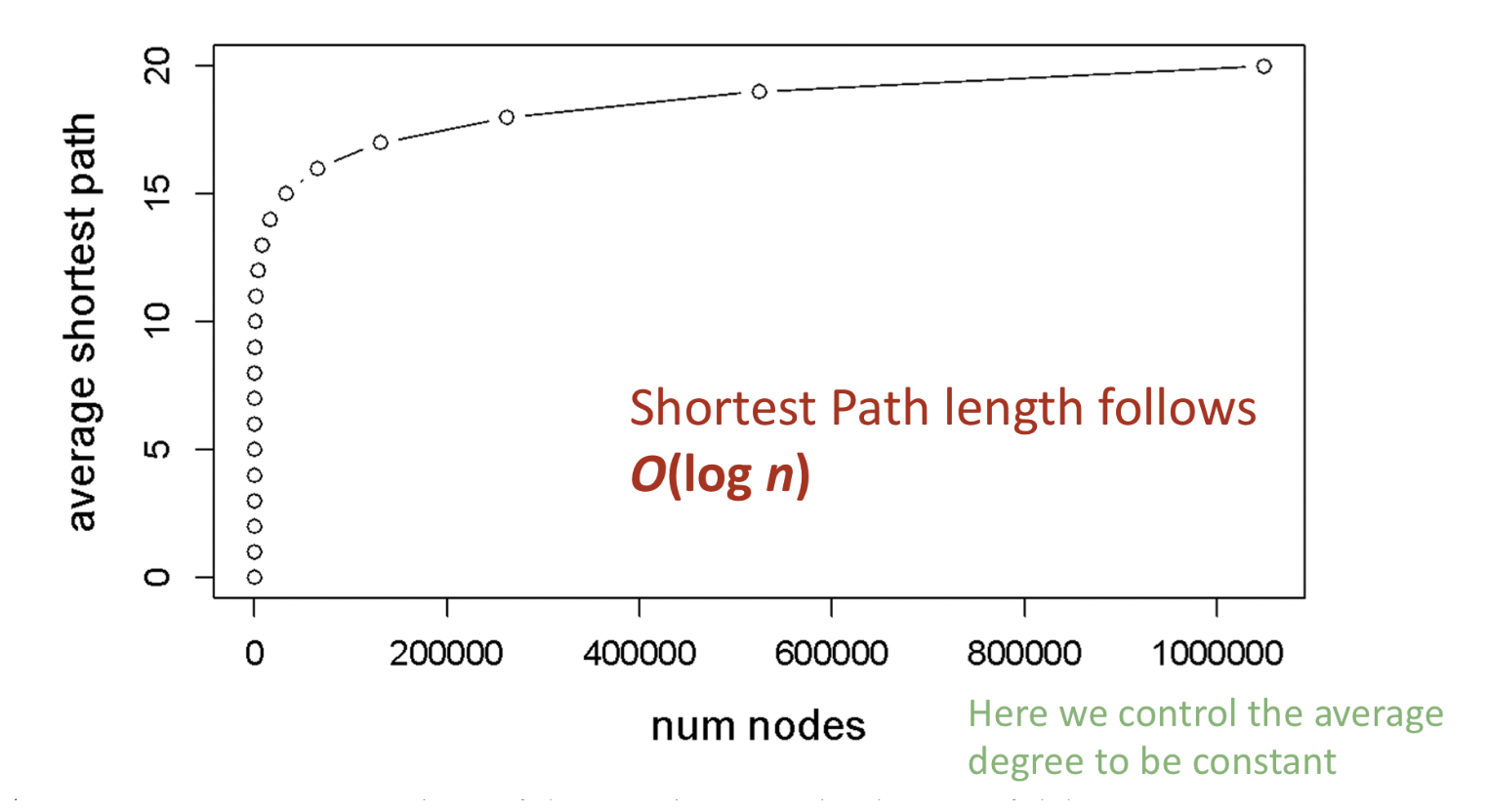
- Gnp의 노드들은 적은 hops만큼 떨어져 있어 O(logn)의 shortest path를 가진다.
Real Networks vs Gnp
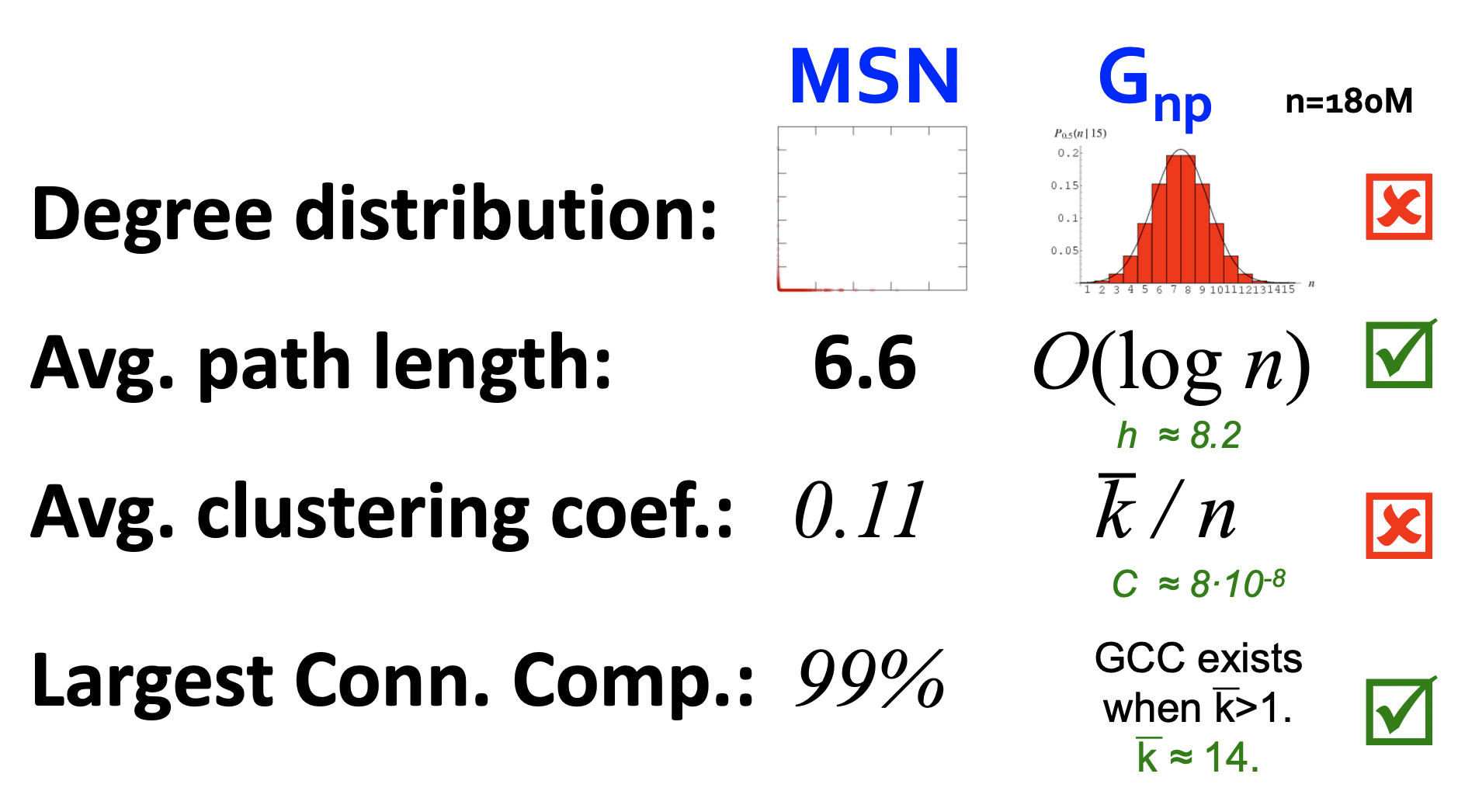
- 실제 그래프와 랜덤 그래프를 비교한 결과 clustering coefficient와 degree distribution이 다르다.
- 실제 그래프의 giant component는 phase transition 형태로 나타나지 않는다. (phase transition은 k=1을 기준으로 giant component가 등장하는 것을 의미)
- Clustering coefficient가 너무 작아 local한 구조가 나타나지 않는다는 단점도 있다.
3. The Small-World Model
Motivation
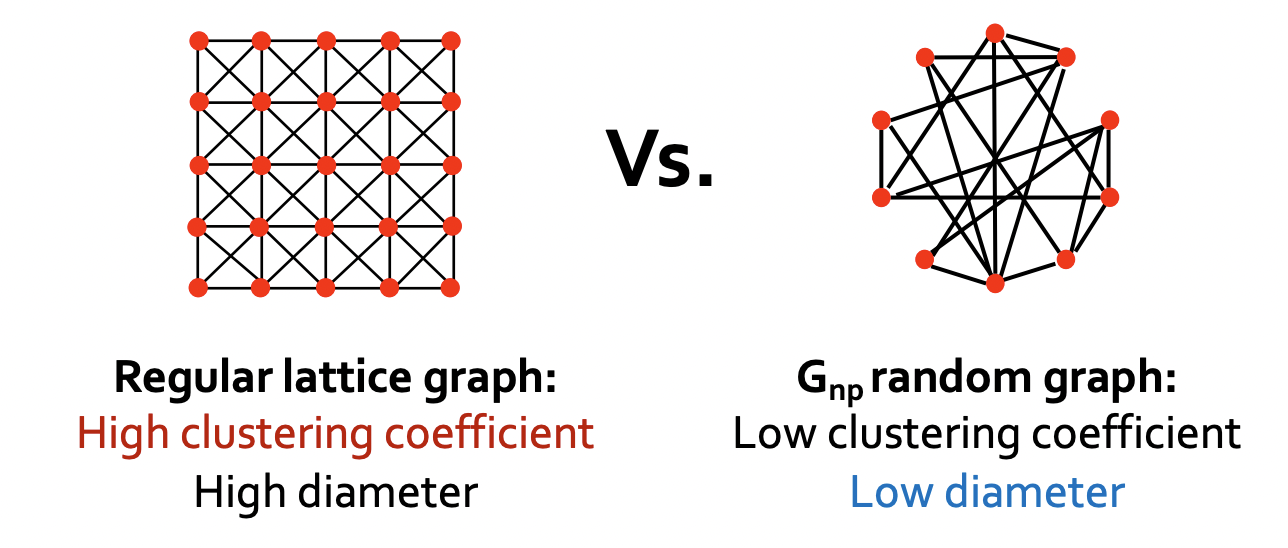
- 실제 그래프는 local한 구조를 가져 clustering coefficient가 높으면서도 낮은 diameter를 가진다.
- Gnp는 낮은 clustering coefficient를 가져 이를 제대로 반영하지 못한다.
Idea
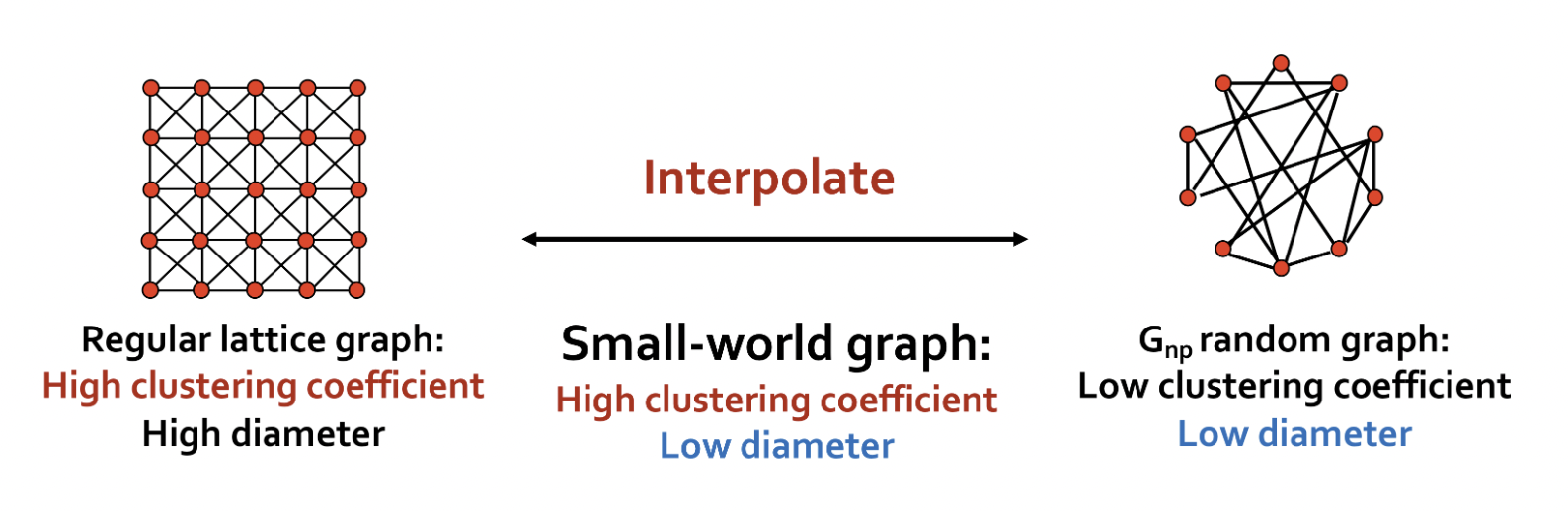
- 높은 clusering coefficient와 큰 diameter를 가지는 regular lattice graph를 interpolation 하여 그래프를 만든다.
Solution
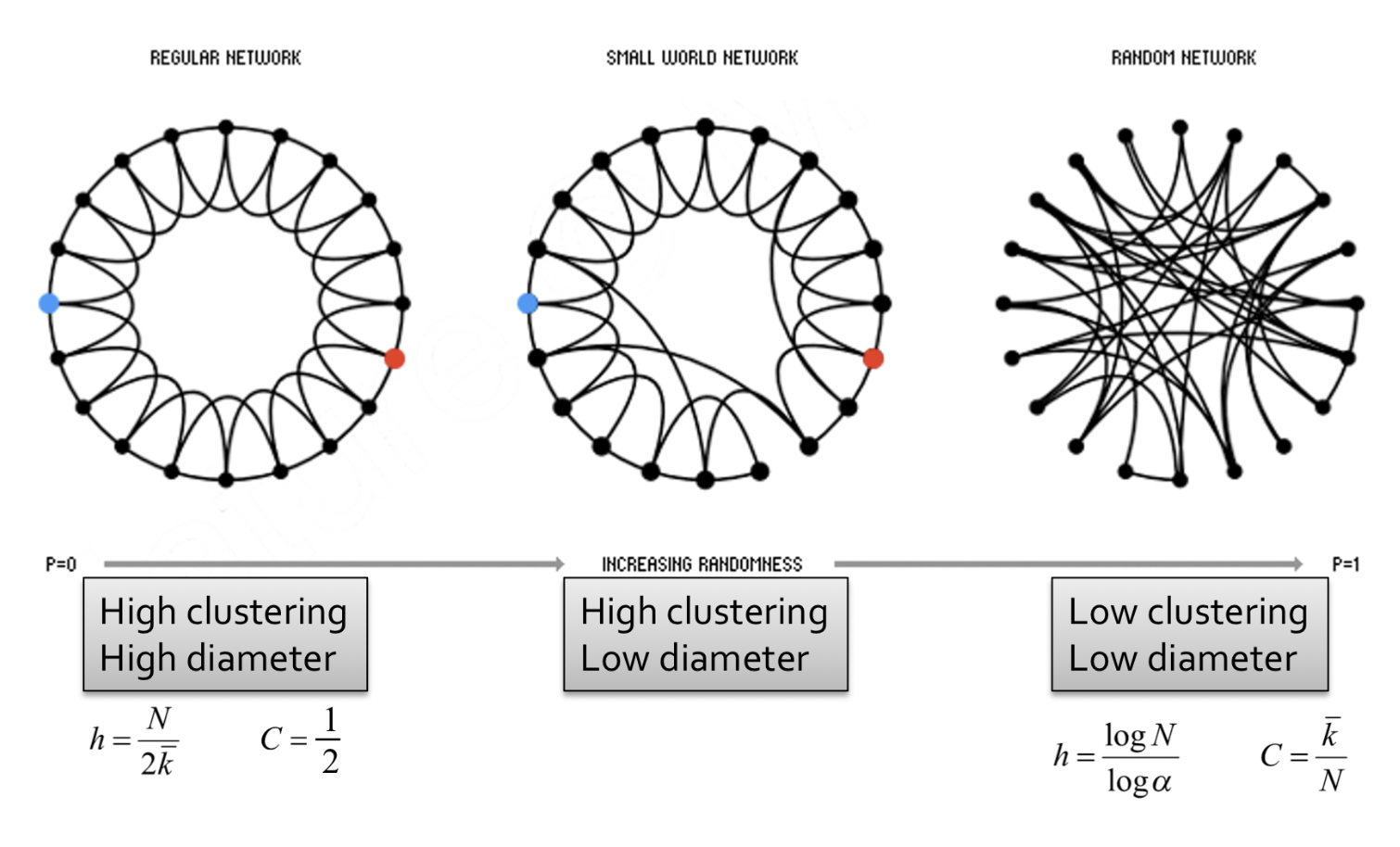
- 이웃 노드와 2-hops인 노드를 이은 low-dimensional regular lattice를 만든다. 이 그래프는 높은 clustering coefficient와 큰 diameter를 가진다.
- 각 엣지의 endpoint를 확률 p에 따라 옮기는 rewiring 과정을 거친다. 이 그래프는 높은 clustering coefficient와 작은 diameter를 가진다.
- Small world networks는 regular network와 random network의 interpolation이라고 할 수 있다.
4. Kronecker Graph Model
Idea
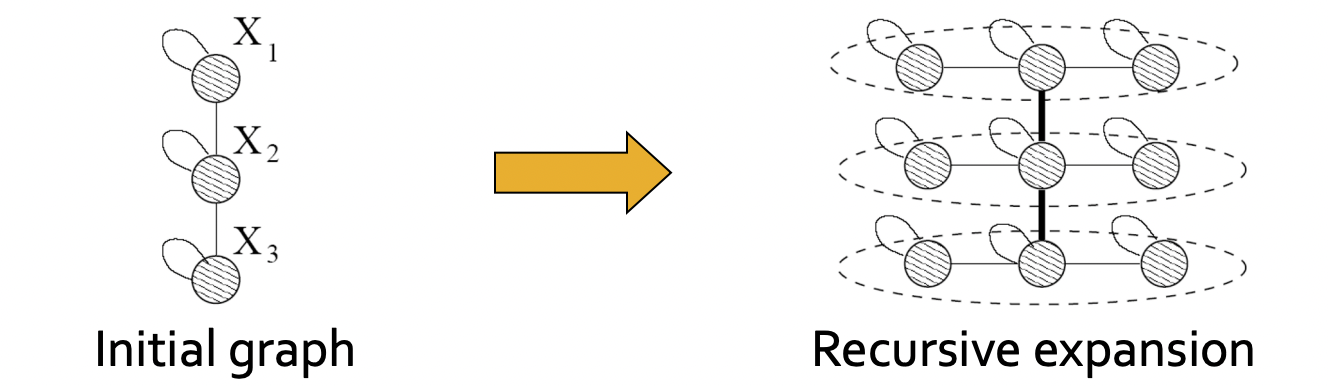
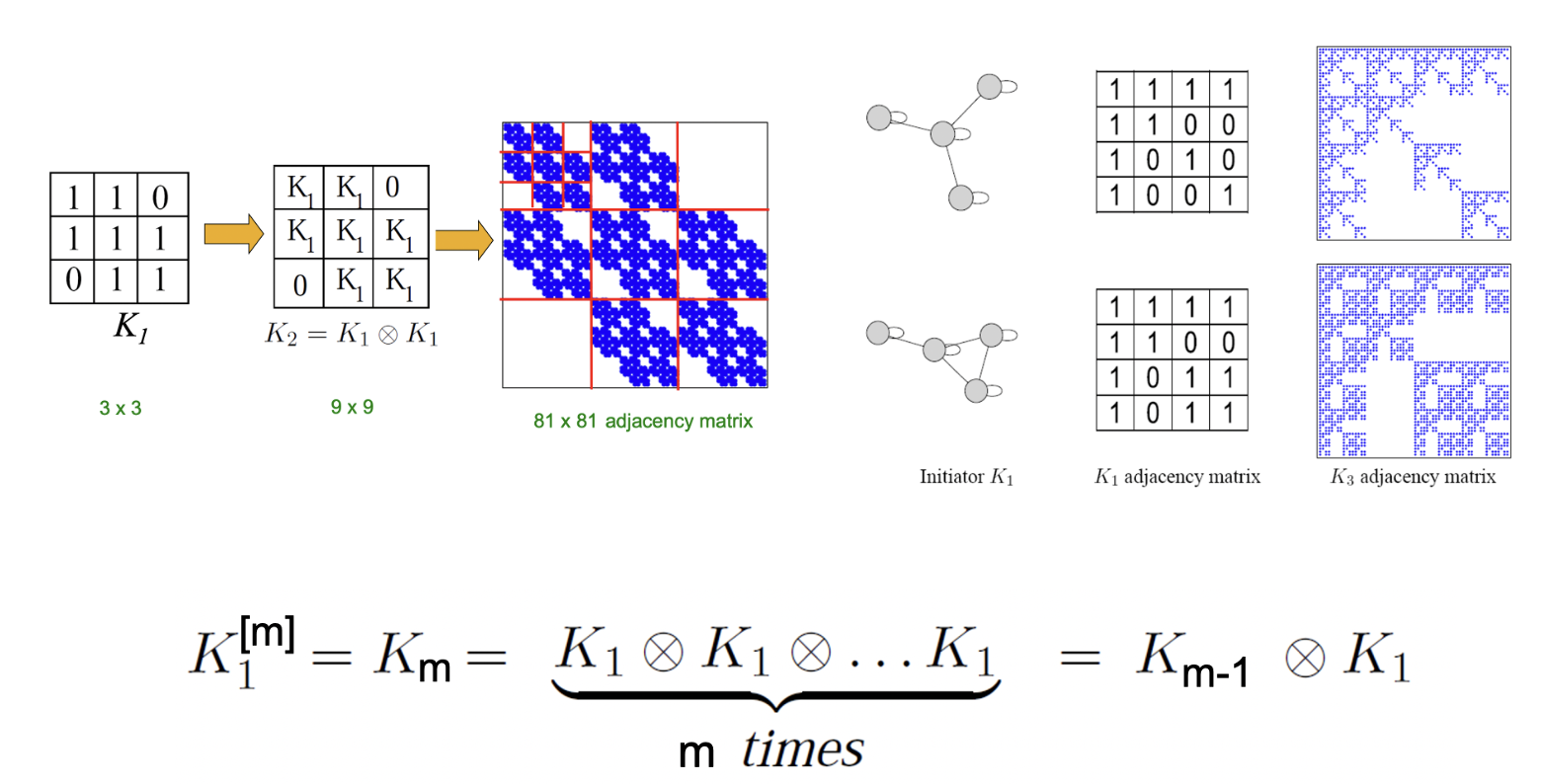
- Object는 자기 자신의 일부와 비슷하므로 네트워크를 재귀적으로 구성할 수 있다.
- Kronecker product를 통해 self-similar 행렬을 만든다.
- Kronecker graph는 kronecker product를 초기 행렬 K1에 반복적으로 행하여 만들 수 있다.
Stochastic Kronecker Graphs

- N1×N1의 확률 matrix θ1을 만든다.
- kth Kronecker power θk를 계산한다.
- θk의 entry puv에 따라 엣지를 생성한다.
- 위 방식은 O(n2)의 시간복잡도를 가져 실제 적용에 어려움이 있다.
- 따라서, 재귀적인 구조를 활용한 더 빠른 방식을 이용한다.
Generation of Kronecker Graphs
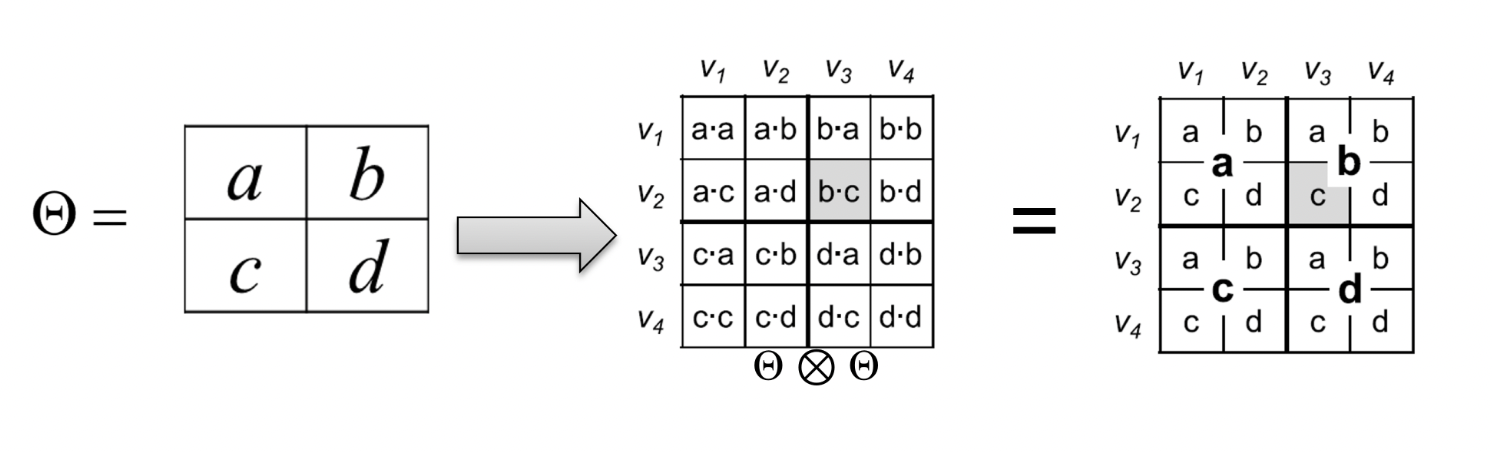
- θ로부터 normalized matrix L을 만든다.
Luv=θuv/(∑opθop)
- L의 확률에 따라 가장 큰 4분할 영역 중 한 영역을 선택한다.
- 그 영역 또한 분할되어 있다면 재귀적으로 확률에 따라 선택한다.
- 단일 cell이 나올 때까지 반복하며 최종적으로 선택되면 1을 할당하여 edge를 만든다.
- 위 과정을 기대 엣지 수 E=(a+b+c+d)m가 될 때까지 반복한다.

- Kronecker Graph가 실제 그래프와 유사함을 확인할 수 있다.
References





















