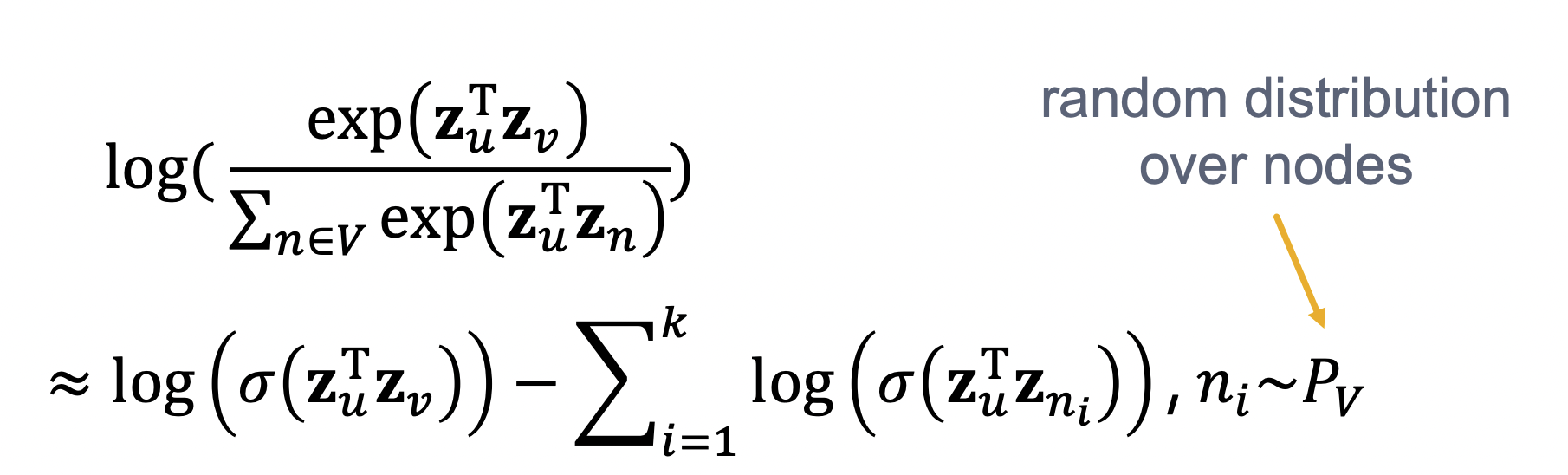1. Node Embeddings

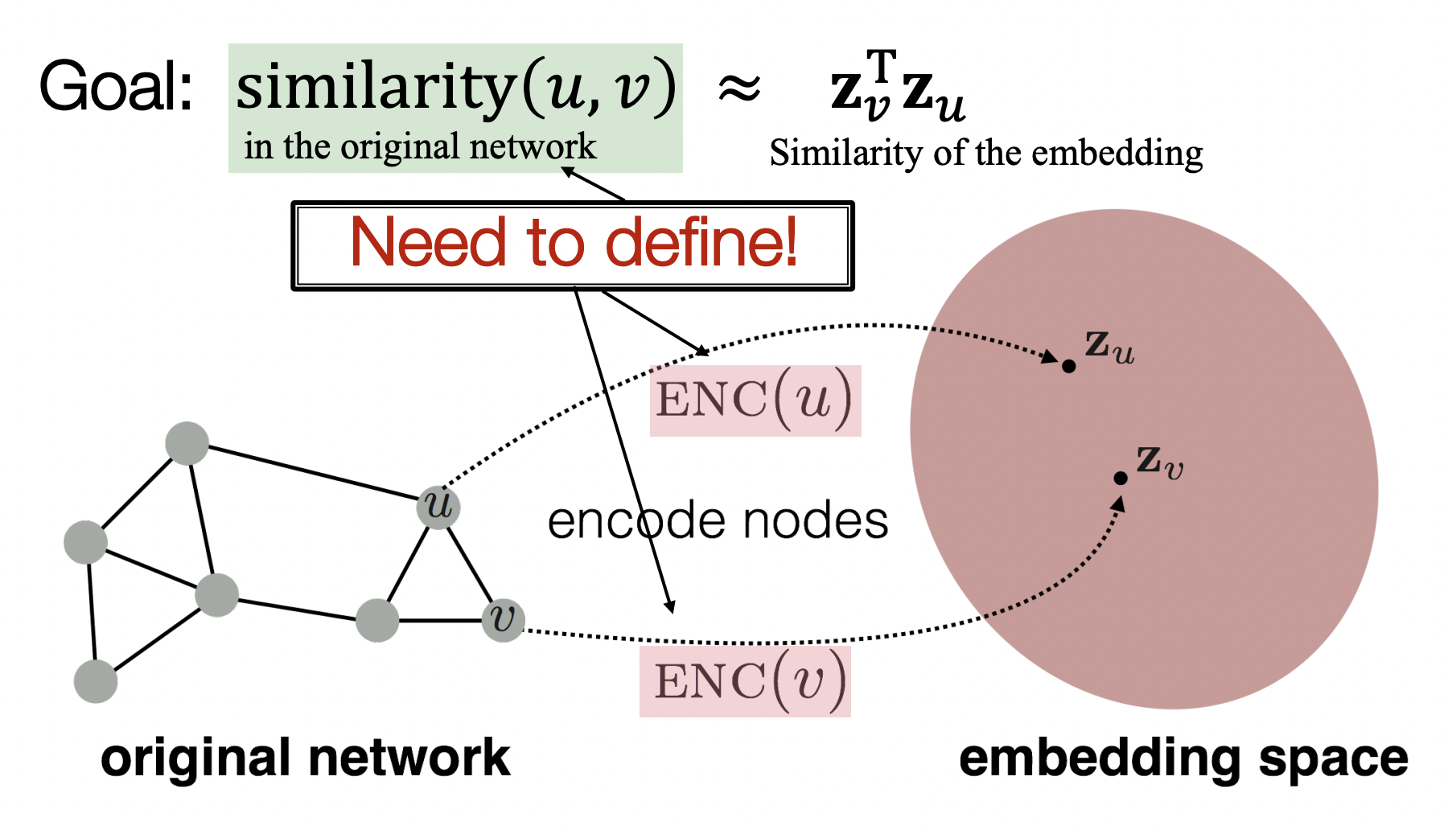
• Encoder를 통해 노드를 low-dimension인 embedding space로 보냈을 때 그 공간에서 비슷한 곳에 위치하는 노드들이 graph 내에서도 유사성을 띄어야 한다.
• 유사성은 두 노드가 연결되어있는가?, 이웃노드를 공유하는가?, 구조적으로 비슷한 역할을 하는가? 등으로 정의할 수 있다.
• 유사성을 측정하기 위한 함수가 필요하며 dot product가 대표적이다.
• 유사한 노드 $(u,v)$의 $z_v^\top z_u$를 최대화하는 것이 objective이다.
  
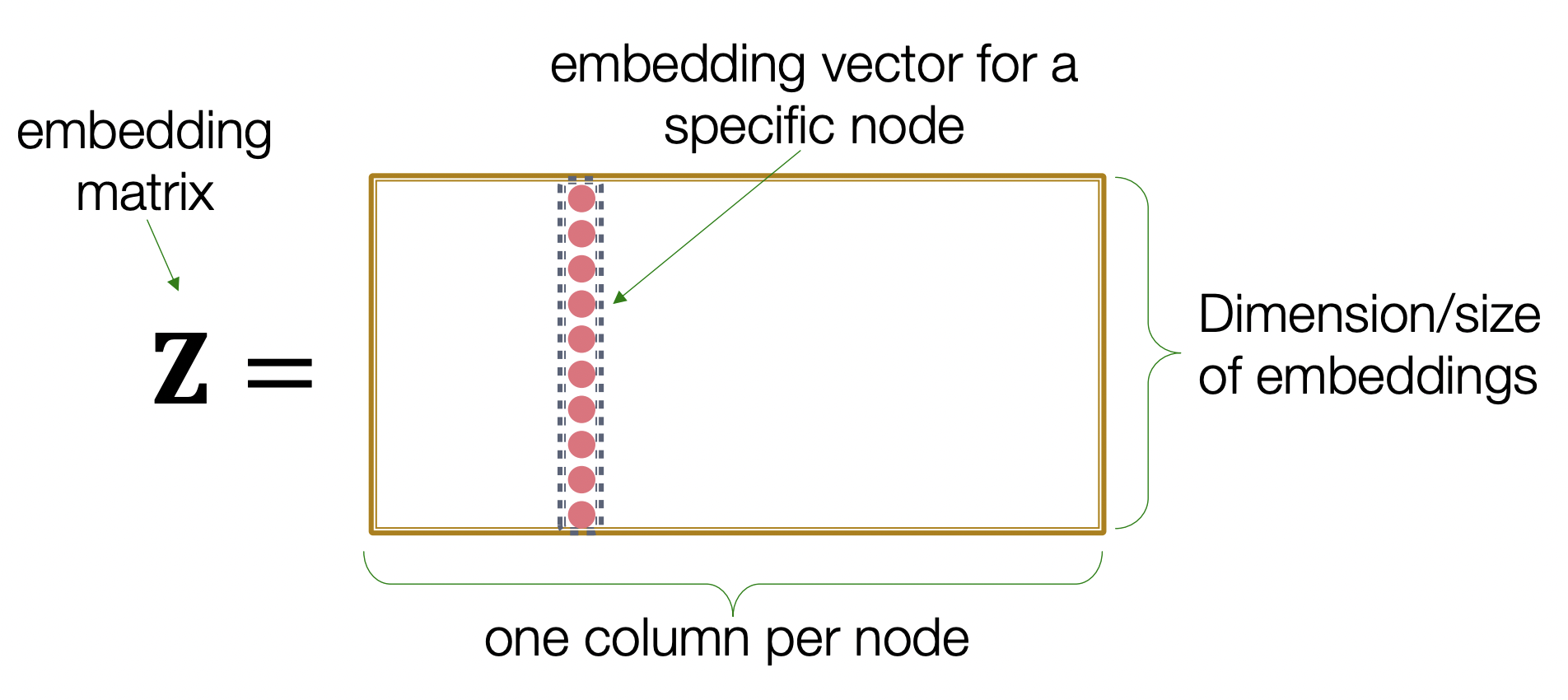
• Encoder는 embedding-lookup matrix로 볼 수 있다.
• $Z$의 열들은 각각 어떤 노드의 embedding vector를 담고있다.

2. Random Walk Approaches for Node Embeddings

Random Walk

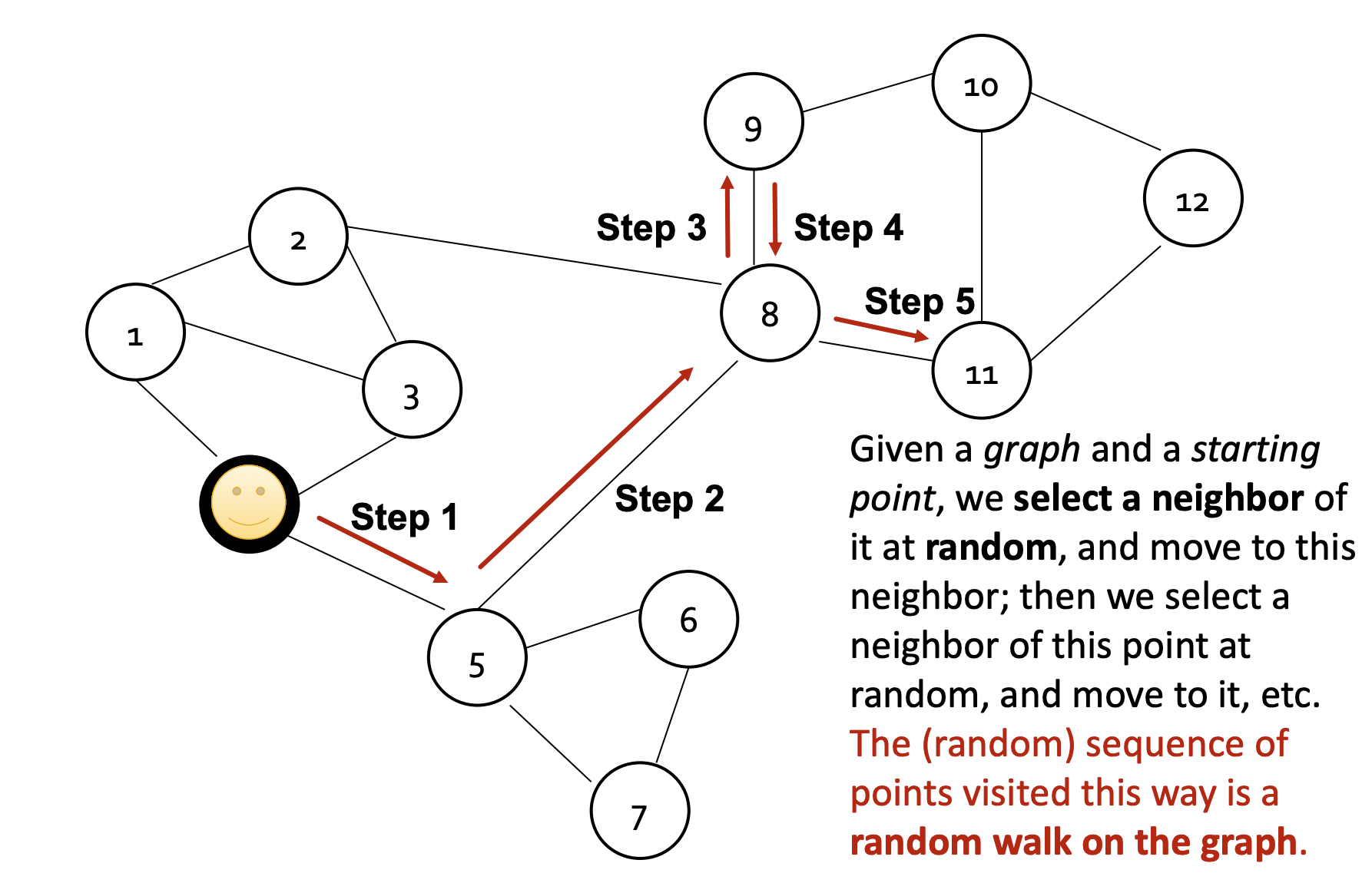
• 시작 노드로부터 반복적으로 이웃 노드를 탐색하는 random Walk 과정을 거친다.
• 무작위로 이동할 수도 있으며 strategy $R$에 의해 이동할 수도 있다.
• $z_u^\top z_v$는 random walk에서 노드 $u$와 $v$가 동시에 발생할 확률을 의미하게 된다.
• Random walk는 다음과 같은 두 가지 특성을 가진다.

  • 표현력(Expressivity): 지역적인 정보와 고차원의 이웃 노드 정보를 전부 활용할 수 있다.
  • 효율성(Efficiency): 모든 노드가 아닌 random walk를 통해 동시에 발생하는 노드 쌍만 고려한다.

Optimization

• 노드 $u$가 주어졌을 때 strategy $R$을 활용한 random walk를 통해 정의된 neighborhood $N_R(u)$가 embedding space 내에서 가까워지도록 학습한다.
• Maximum liklihood objective가 되며 $P(v|z_u))$는 노드 $u,v$가 동시에 발생할 확률로 softmax로 바꿀 수 있다.
  
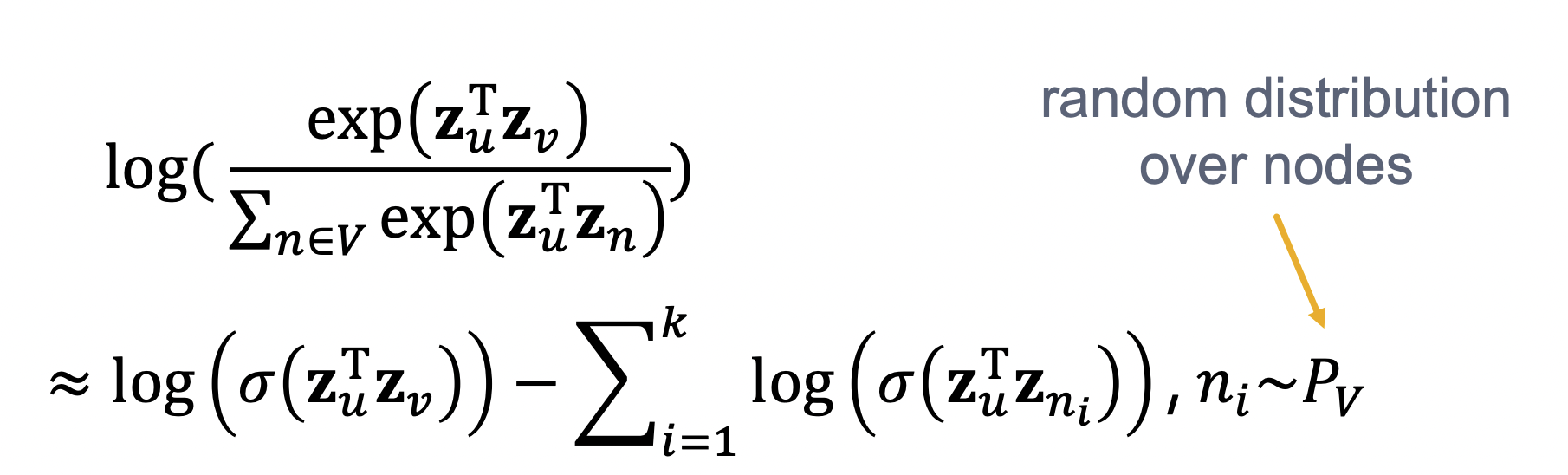
• 위 방식은 계산량이 너무 많기 때문에 sigmoid 함수로 근사시키며 negative sampling을 활용한다.
• Negative sampling이란 확률에 기반하여 negative 노드를 $k$개만 뽑아내는 방식으로 그래프에서는 degree에 비례하여 확률을 부여한다.

node2vec

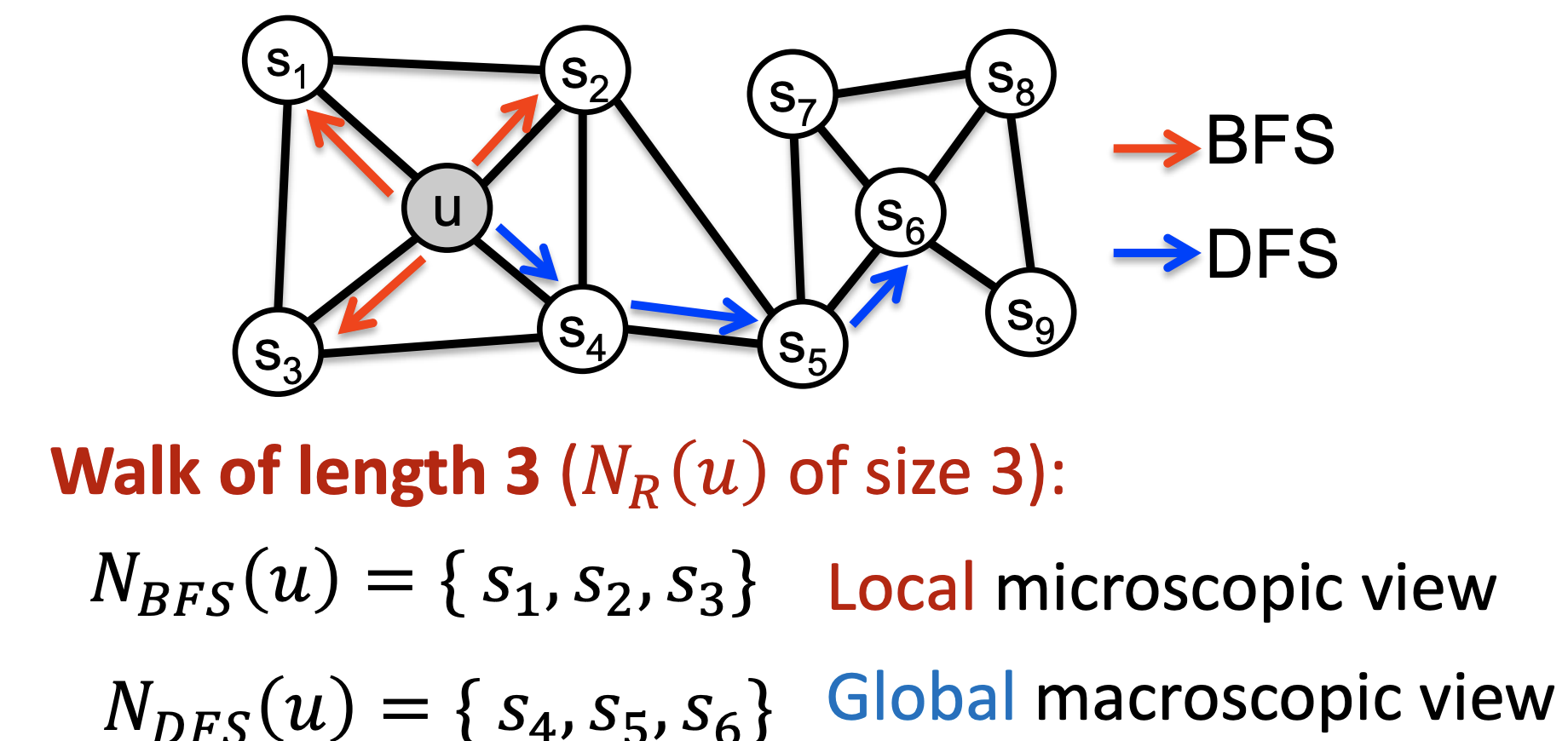
• 무작위로 탐색하는 방식은 먼 거리까지 갈 확률이 너무 낮으므로 이를 보완할 수 있는 biased 2nd order strategy $R$을 사용한다.
• Local한 영역은 BFS를 통해, Global한 영역은 DFS를 통해 탐색할 수 있다.
  
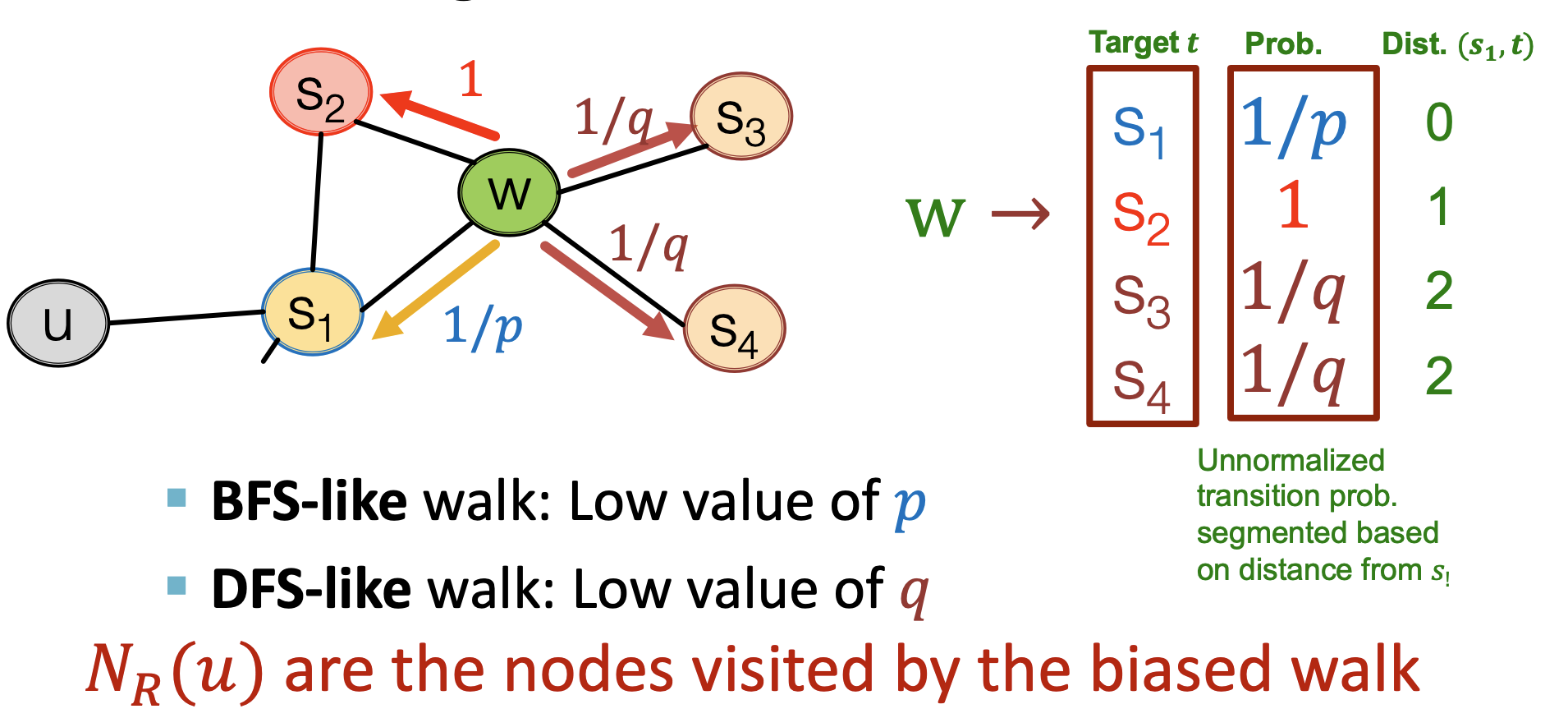
• 이전 node로 돌아가는 것에 대한 return parameter $p$와 BFS와 DFS의 비율에 대한 in-out parameter $q$가 존재한다.
• $S_1$에서 $W$로 왔을 때 다시 $S_1$으로 돌아갈 확률은 $1/p$, distance가 1인 $S_2$로 갈 확률은 1, 더 먼 거리인 $S_3, S_4$로 갈 확률은 $q/1$이 된다.

3. Embedding Entire Graphs

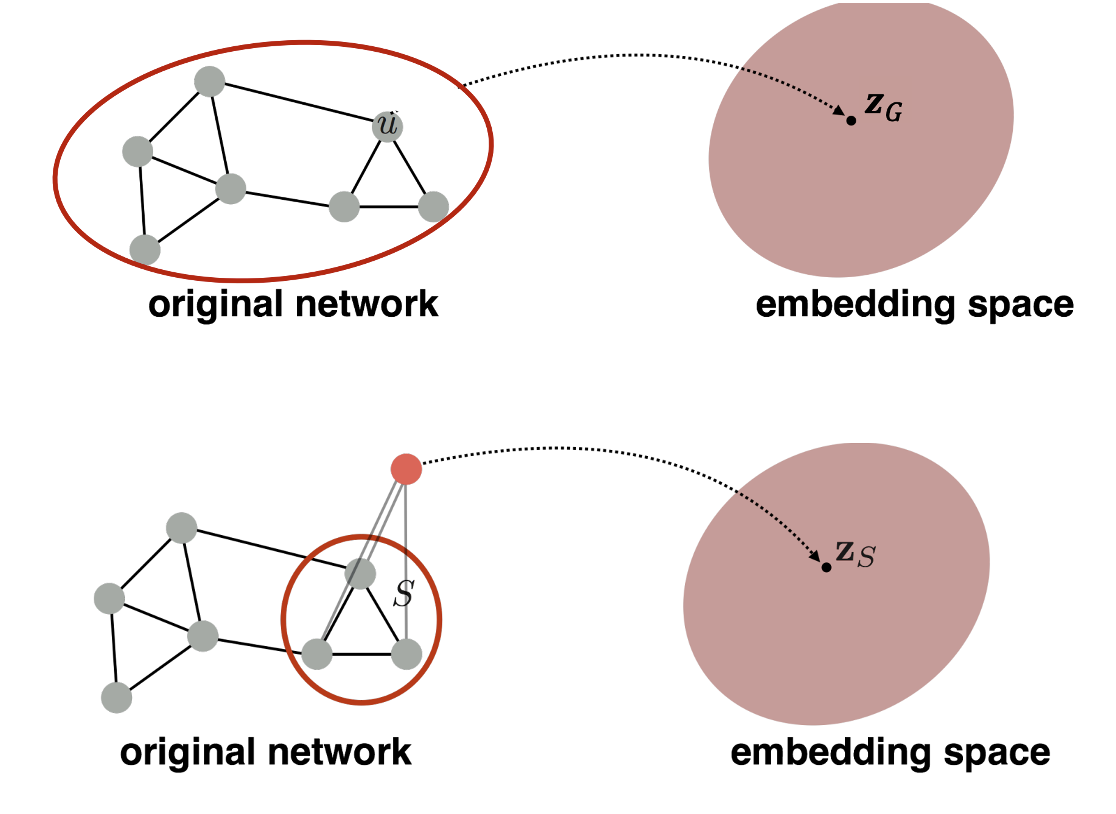
• Subgraph 혹은 전체 그래프를 embedding시키는 방법
• 단순하게는 embedding node $z_v$의 합 혹은 평균을 $z_G$로 정의하거나 virtual node를 만들어 임베딩시키는 방식이 있다.

Anonymous Walk Embeddings

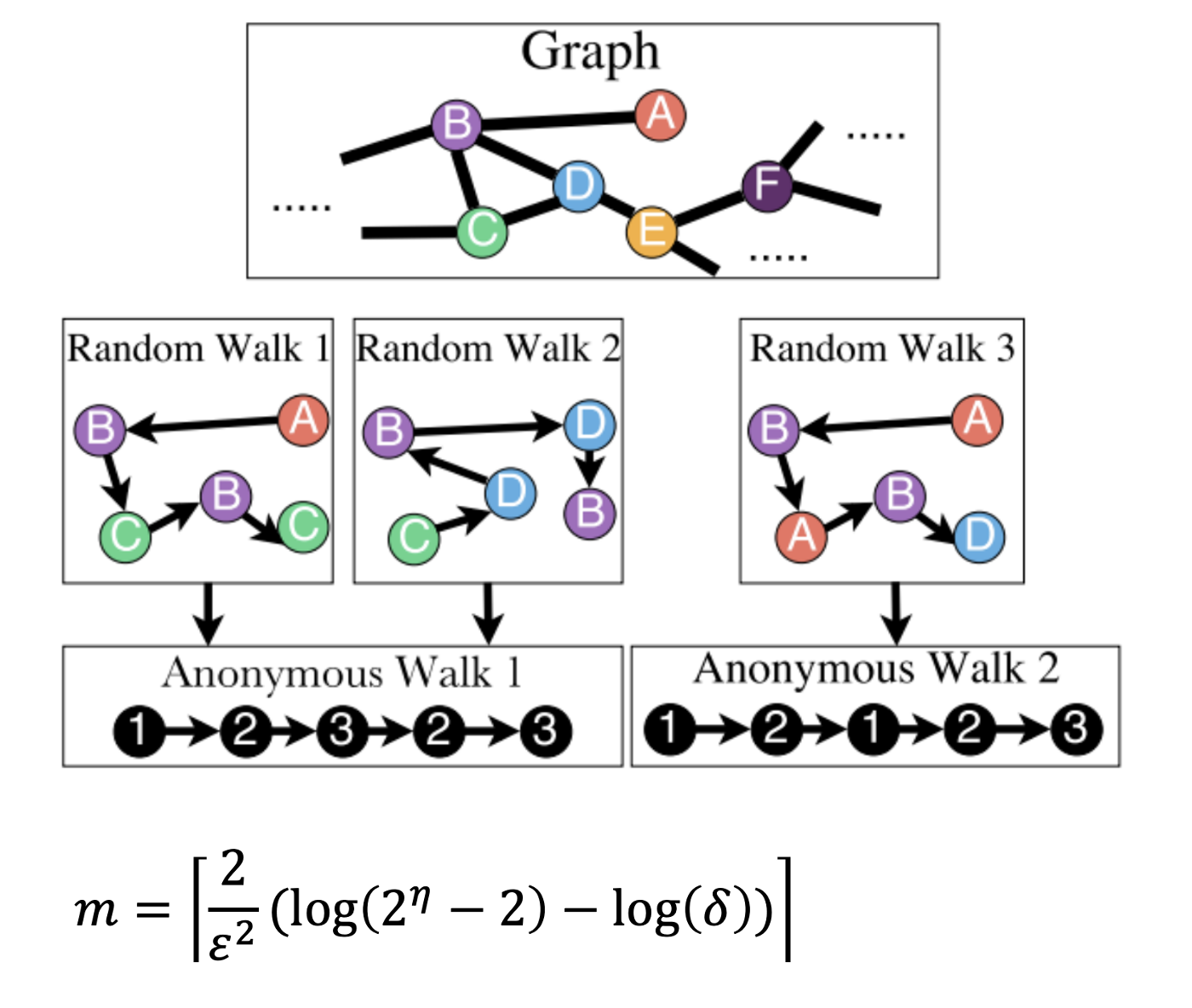
• Anonymous walk는 random walk를 통해 경로의 index를 기록하여 그 횟수를 embedding으로 표현하는 방식이다.
• node=index가 아니며 새로운 노드가 나올 때마다 index는 +1이 되므로 Random Walk1과 2의 Anonymous Walk는 동일하다.(즉, 노드가 익명이다)
• 예를 들어, length가 3일 경우 anomous walk $w_i$는 111, 112, 121, 122, 123 총 5가지가 된다.
• $m$번 random walk를 실행했을때 $Z_G$는 $w_i$의 빈도가 담긴 5차원 벡터가 된다.
• 적절한 실행횟수 $m$은 위 공식을 통해 구하며 $\epsilon$은 오차 하한, $\delta$는 오차 상한, $\eta$는 길이가 $l$일 때 anonymous walk $w_i$의 수를 의미한다.
• 하지만 이러한 방식으로 전체 그래프를 embedding하기에는 length에 따라 anonymous walks의 수가 지수적으로 증가하기 때문에 어려움이 있다.

New idea: Learn Walk Embeddings

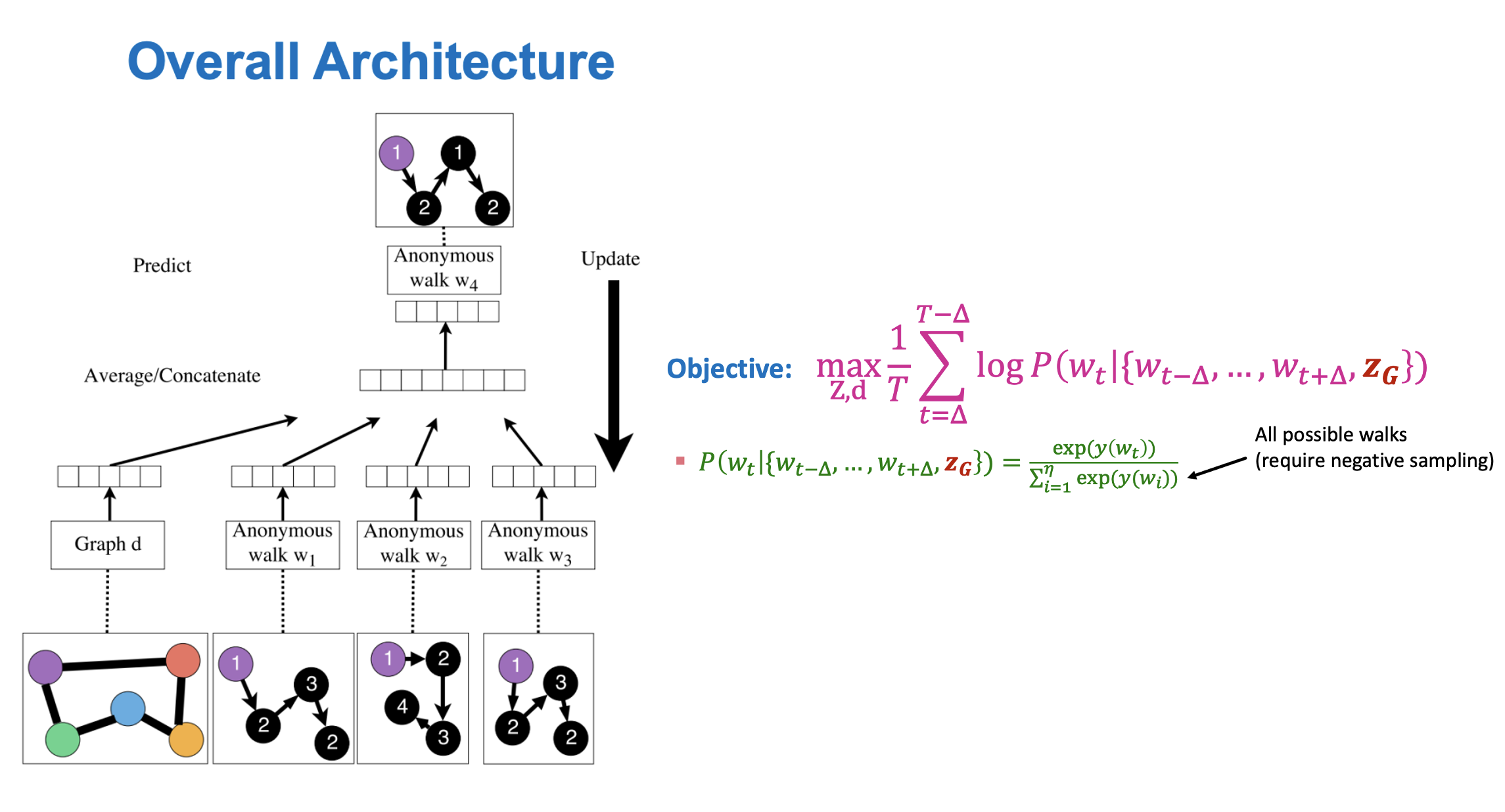
• Walk 또한 임베딩하여 나타내는 방법으로 역전파를 활용해 $Z_G$를 학습한다.
• Window size가 $\vartriangle$일 때 동일한 노드에서 출발한 $w_{t-\vartriangle}, ..., w_{t+\vartriangle}$를 이용해 $w_t$를 예측한다.
• 그래프 벡터 $d$와 $w_i$들이 concatenation되어 입력으로 사용되며 softmax를 통해 예측한 결과와의 loss를 통해 역전파되어 학습한다.

References

• Lecture 3.1: https://www.youtube.com/watch?v=rMq21iY61SE&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=7
• Lecture 3.2: https://www.youtube.com/watch?v=Xv0wRy66Big&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=8
• Lecture 3.3: https://www.youtube.com/watch?v=eliMLfJeu7A&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=9