Introduction
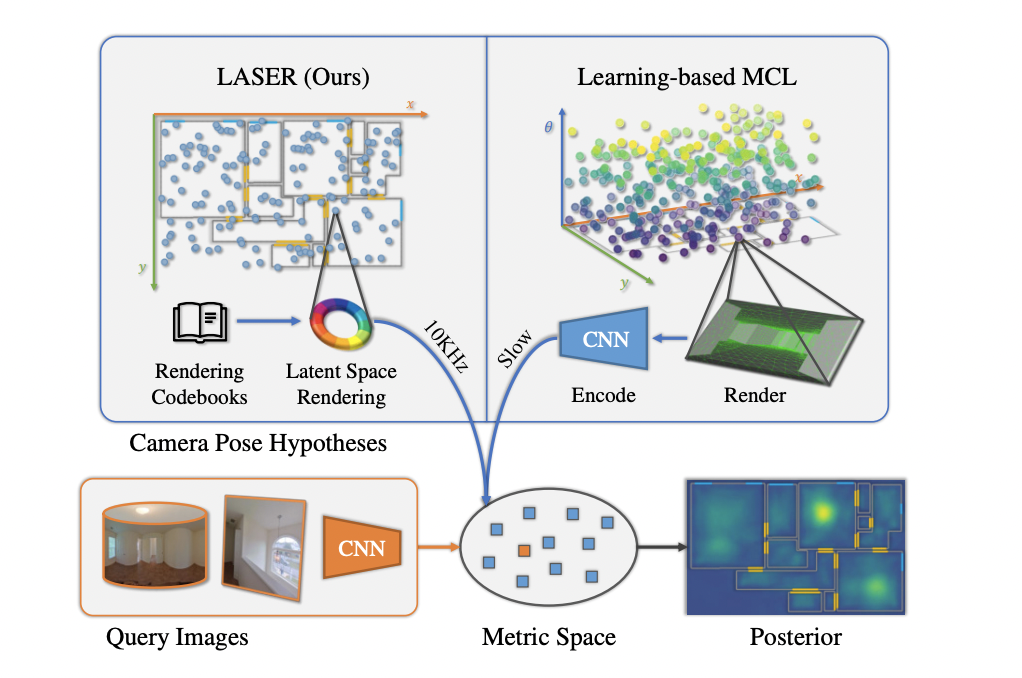
- 본 연구에서는 Monte Carlo Localization(MCL) framework를 활용해 2D floor map에 대한 query panorama/perspective image가 주어졌을 때 camera pose를 찾는다.
- MCL은 generative framework에 근거하여 샘플링 한 camera pose를 rendering 하였을 때 query obsevation과 가장 유사해지도록하는 maximum likelihood search를 활용한다.
- 하지만, conventional한 MCL methods의 경우 depth sensor를 요하며 explicit한 geometric modeling으로 인해 환경 변화에 robust하지 못하다는 단점이 있다.
- Synthesized와 query observation에 대해 모두 latent space를 학습하는 supervised learning 방식의 경우 computation cost가 크며 latent space representation이 geometrical한 해석이 불가하다는 단점이 있다.
- 따라서, 본 연구에서는 rasterized 2D floor map로부터 바로 feature를 렌더링하여 geometric한 의미가 있으며 효율적인 circular feature를 제안한다.
Method
Problem Formulation
-
Reference map 에 대한 query image 가 FoV와 함께 주어질 때 2D pose 를 추정하고자 한다.
-
General MCL은 measurement model을 로 정의하며 이는 map 상의 camera pose 에 의해 관측되는 image 의 likelihood를 의미한다.
-
베이즈 정리에 따라 MCL은 posterior distribution 를 추정한다. 는 normalization constant로 무시할 수 있으며 )는 prior camera pose distribution으로 uniform distribution을 가정한다.
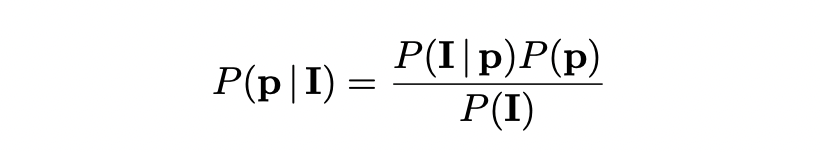
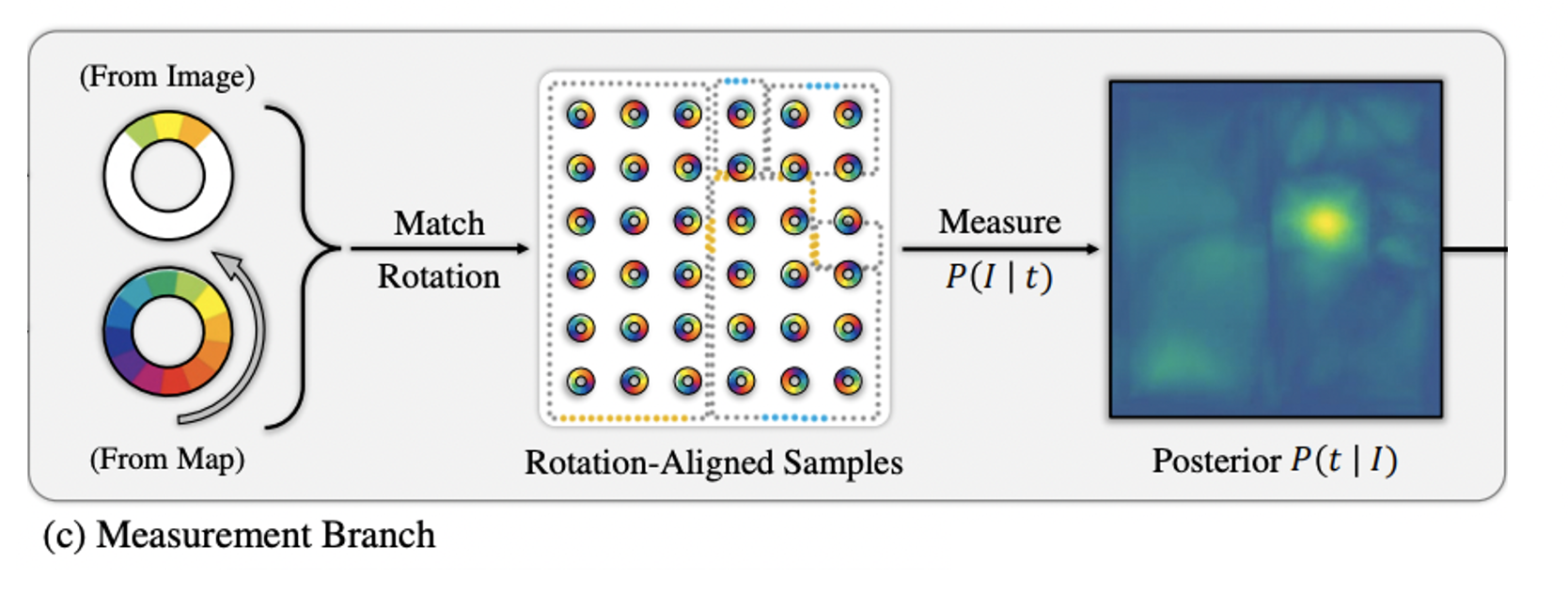
-
Query image와 camera pose hypotheses 두 개의 도메인의 similarity를 측정하기 위해 동일한 space에서의 deep metric learning을 활용한다.
-
Geometric한 구조를 담기 위해 일반적인 flattened descriptor 대신 circular feature를 활용한다.
-
는 feature segment의 수를 의미하며 는 범위의 local direcitonal FoV를 인코딩한다.
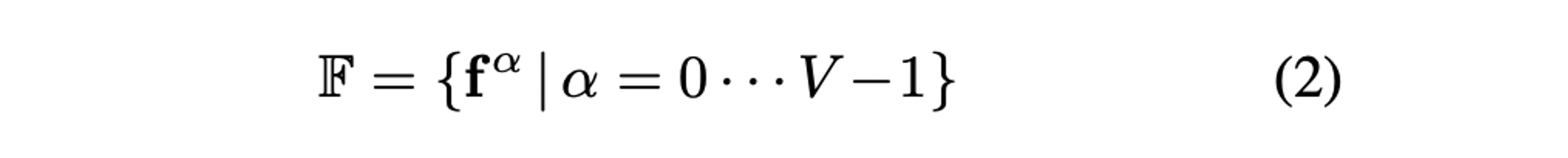
- 두 circular features의 similarity는 cosine을 통해 계산한다.
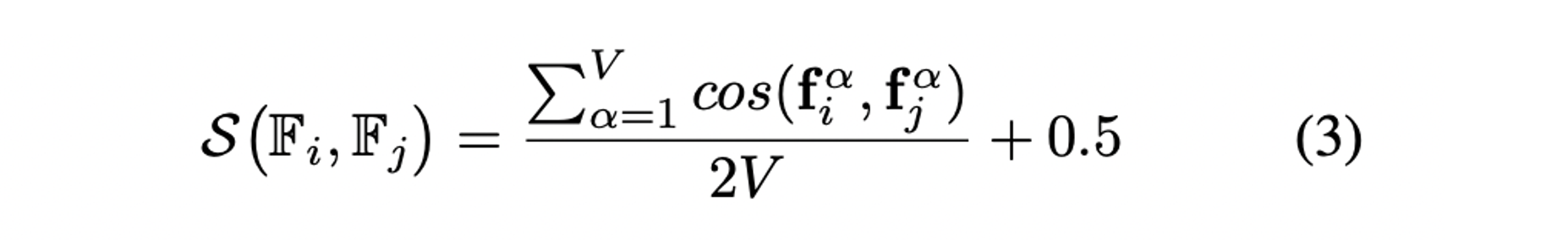
- 또한, angle 가 주어졌을 때 circular feature 의 rotation 정보를 rotating operator 를 통해 정의한다.
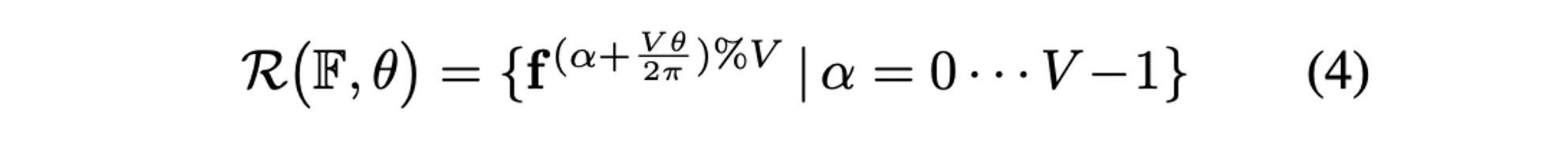
- 최종적인 measurement model은 다음과 같으며 는 PDF normalization constant를, 는 query image와 map 상의 location 로부터 렌더링한 circular feature를 의미한다.
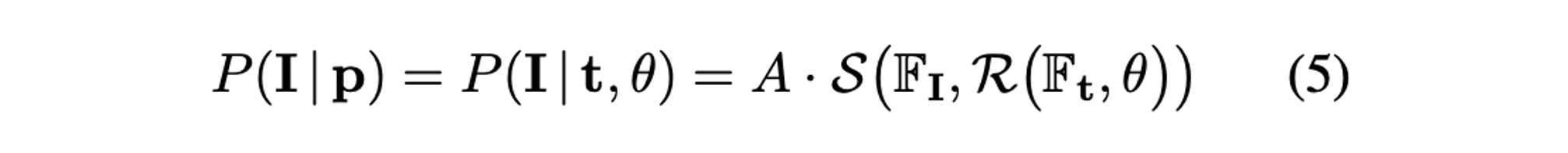
- Camera pose에 대해 아주 많은 sampling이 필요하지만 canonical orientation을 가진 locatio 만 sampling을 하며 uniform하게 회전시키며 best를 저장하여 최적화 한다.
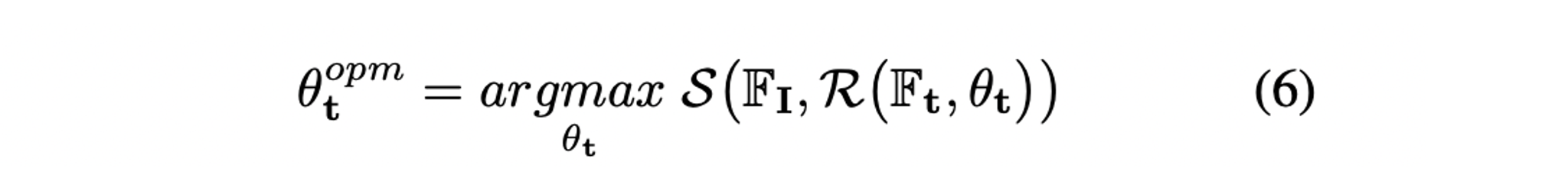
- 따라서 식(5)의 measurement model은 다음과 같이 표현된다.
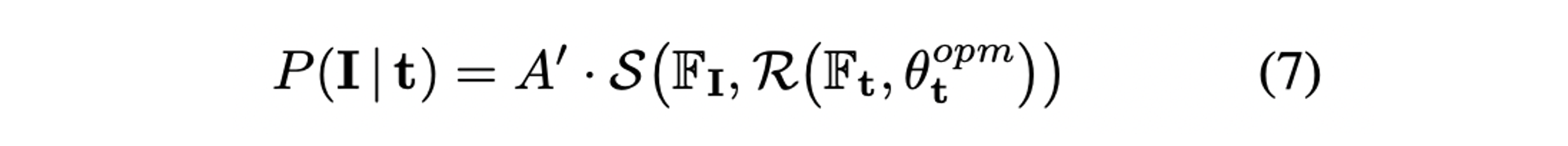
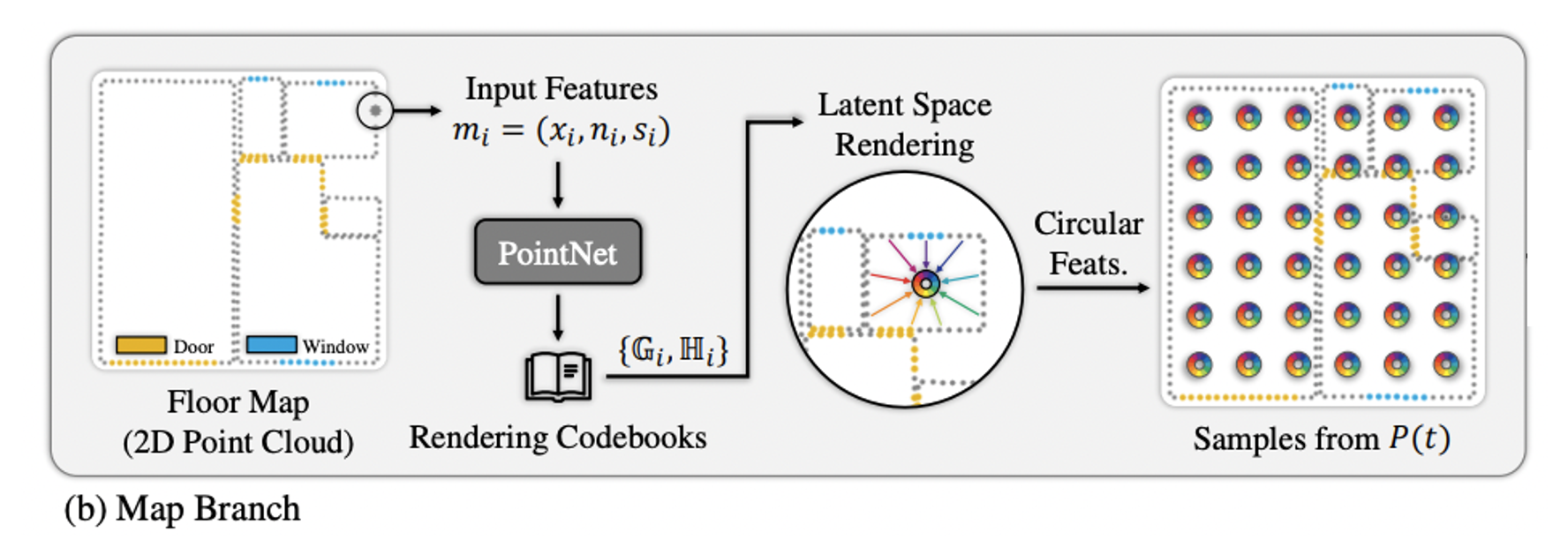
Map Branch
-
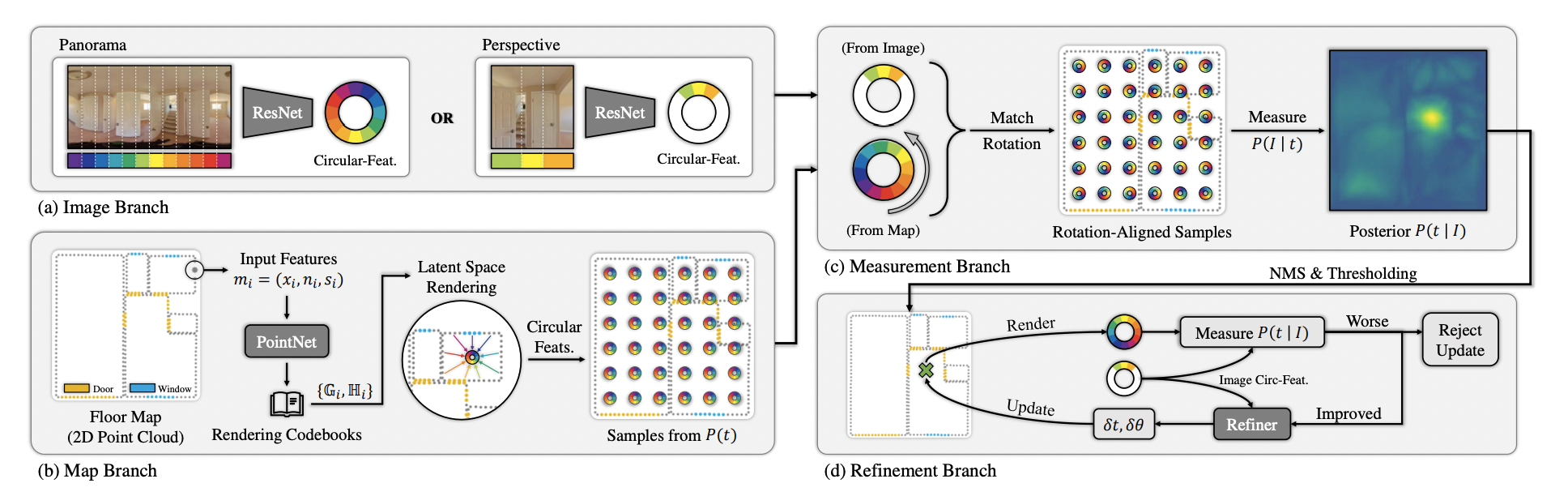
Floorplan이나 occupancy grid 같이 occupancy 정보를 가지고 있는 2D map representation 으로부터 point들을 smapling하여 2D point cloud 을 만든다.
-
각 point 는 location, normal vector, optional semantic information을 인코딩한다.
-
2D variant of PointNet을 활용하여 각 point 마다 distance에 대한 feature 과 incident-angle에 대한 feature 를 담은 codebook을 만든다. codebook은 렌더링할 때 활용된다.
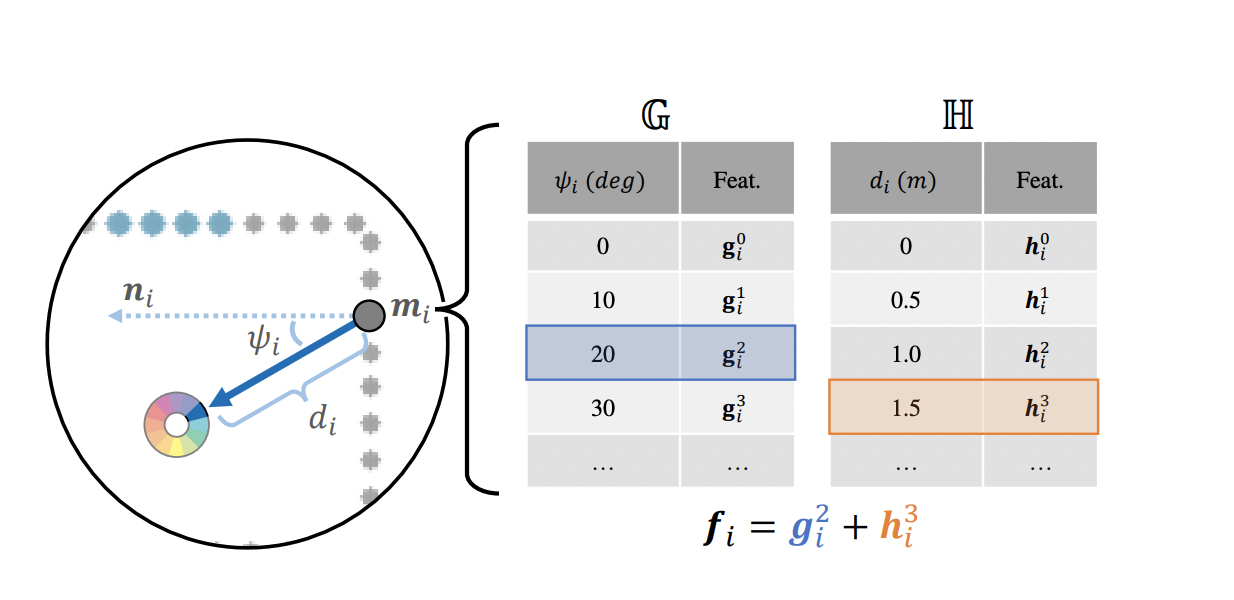
-
라 할 때 distance 와 incident-angle 는 아래 식에 의해 구할 수 있으며 feature 는 로 표현할 수 있다. 는 pre-defined maximum distance를 의미한다.
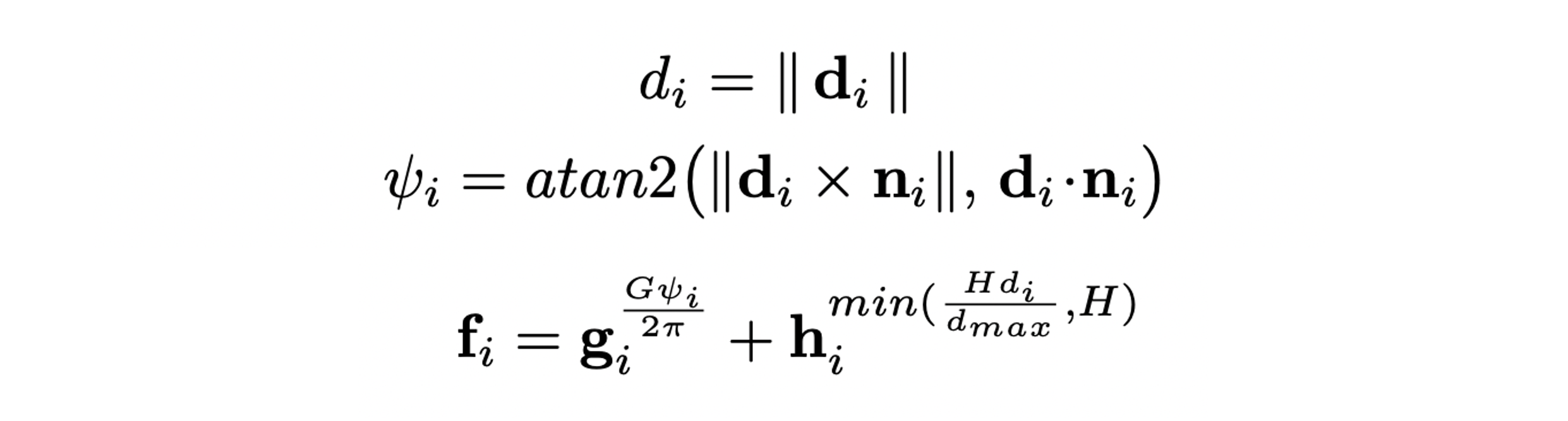
-
식(4)와 유사하게 non-integer indexing에 대해서는 가까운 두 code를 linera interpolation하여 구한다.
-
가 visibility test를 통과하면 를 아래 식에 의해 circular feature 로 투영하며 투영된 point들은 각 segment별로 average 된다. 는 viewing ray의 각도를 의미한다.
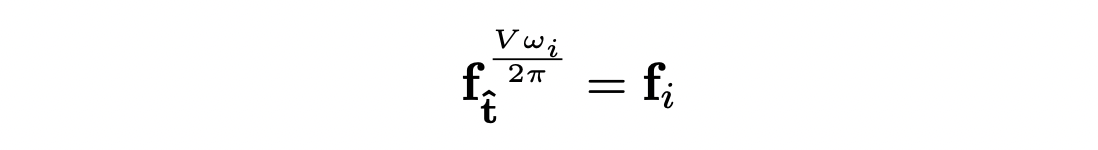
Image Branch

- Panorama에서 column은 horizontal FoV를 의미하기 때문에 ResNet50 encoder를 거친 feature를 vertical dimension average pooling하여 circular segments의 feature dimension으로 맞춰준 뒤 horizontal direction으로도 average pooling하여 segment의 수로 맞춘다.
- Perspective image에 대해서는 FoV와 지면에 대한 zero pitch/roll angle을 안다고 가정하며 rectification을 수행한다. Panorama와 동일한 네트워크를 활용하며 feature가 없는 FoV 밖의 영역에 대해서는 마스킹을 한다.
Refinement Branch
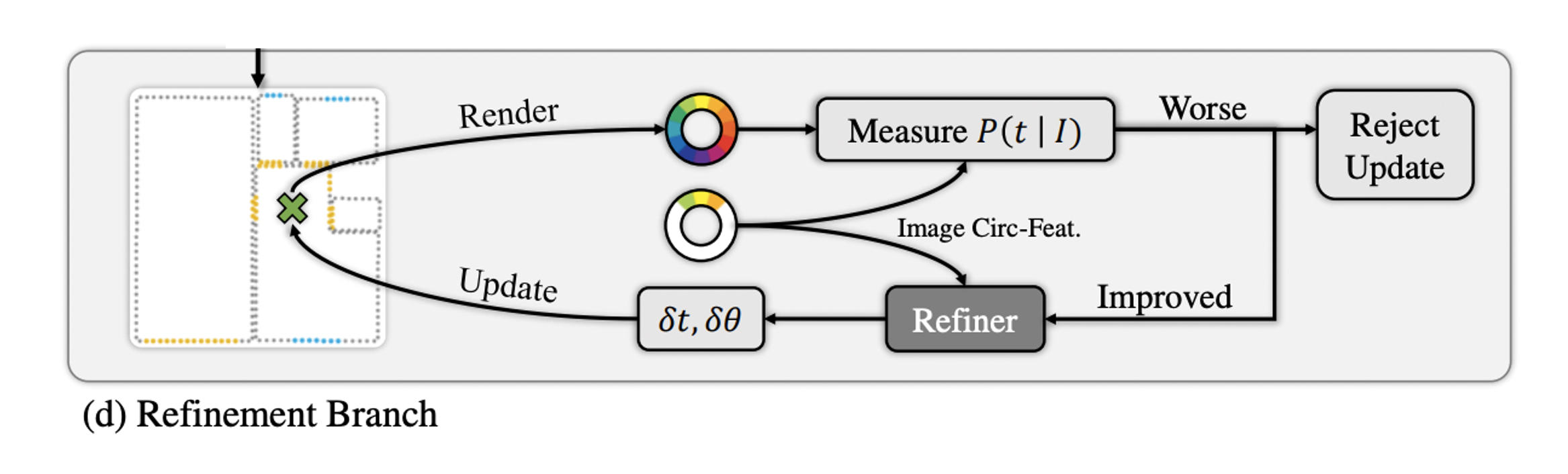
- 앞서 ligh-weight continuous하게 추정한 에 대해 circular features 와 를 refinement branch의 input으로 받는다.
- 1D convolution layer와 FC layer를 거쳐 translation과 rotation에 대한 offset 를 예측한다.
- 이후 새로 update 된 circular feature 를 렌더링하여 와의 similarity를 계산한다.
- 계산한 score가 original camera pose의 score보다 높으면 accept하며 그렇지 않으면 refinement가 수렴했다고 볼 수 있다.
Loss
-
Triplet loss를 통해 를 anchor로 하여 GT camera pose에 대한 circular feature 와는 positive가 되도록, random하게 sampling한 camera pose에 대한 circular feature 와는 negative가 되도록 학습한다.
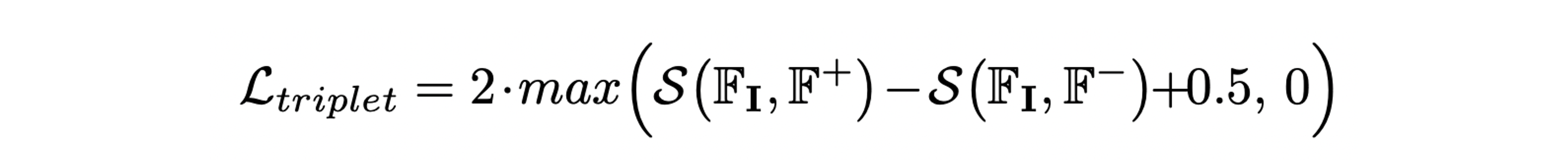
-
Similarity function 와 triplet loss는 모두 elementwise한 비교를 하기 때문에 context 정보를 담지 못한다.
-
따라서, normalized feature segment의 평균인 를 활용한 context loss를 제안한다.
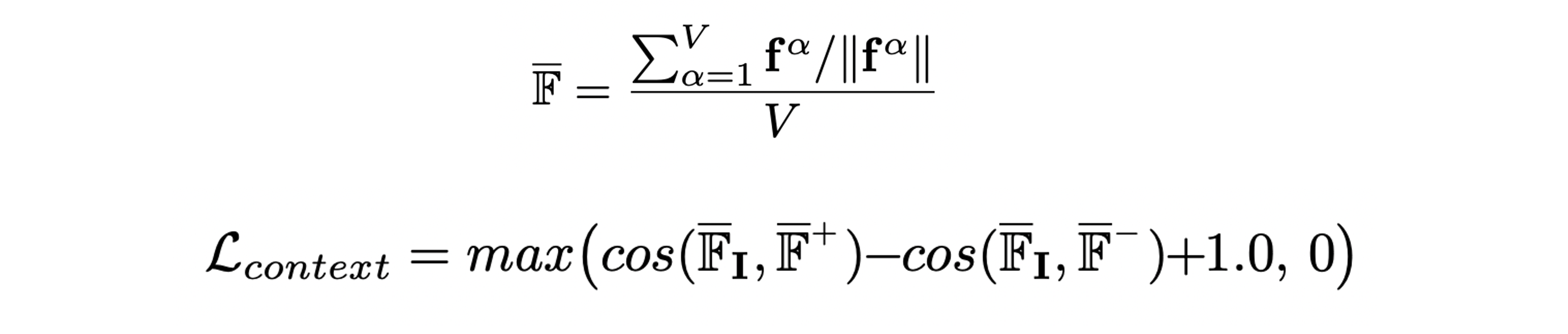
-
Refinement branch에서는 GT camera pose로부터 0.5m radius, 30 degree angle 이내에서 sampling한 circular features를 활용해 regression 한다.
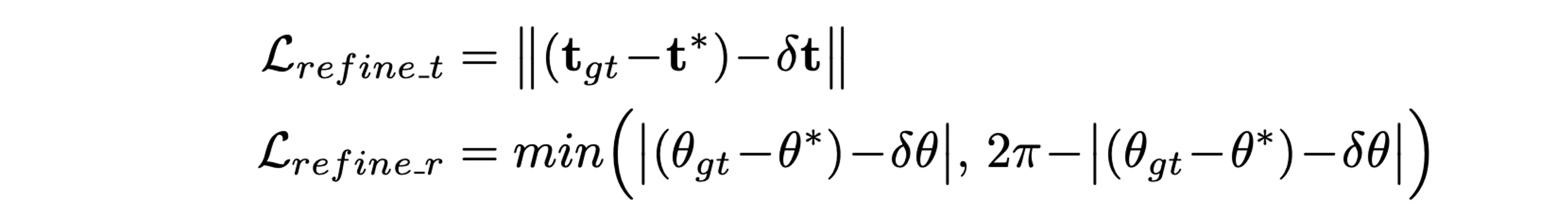
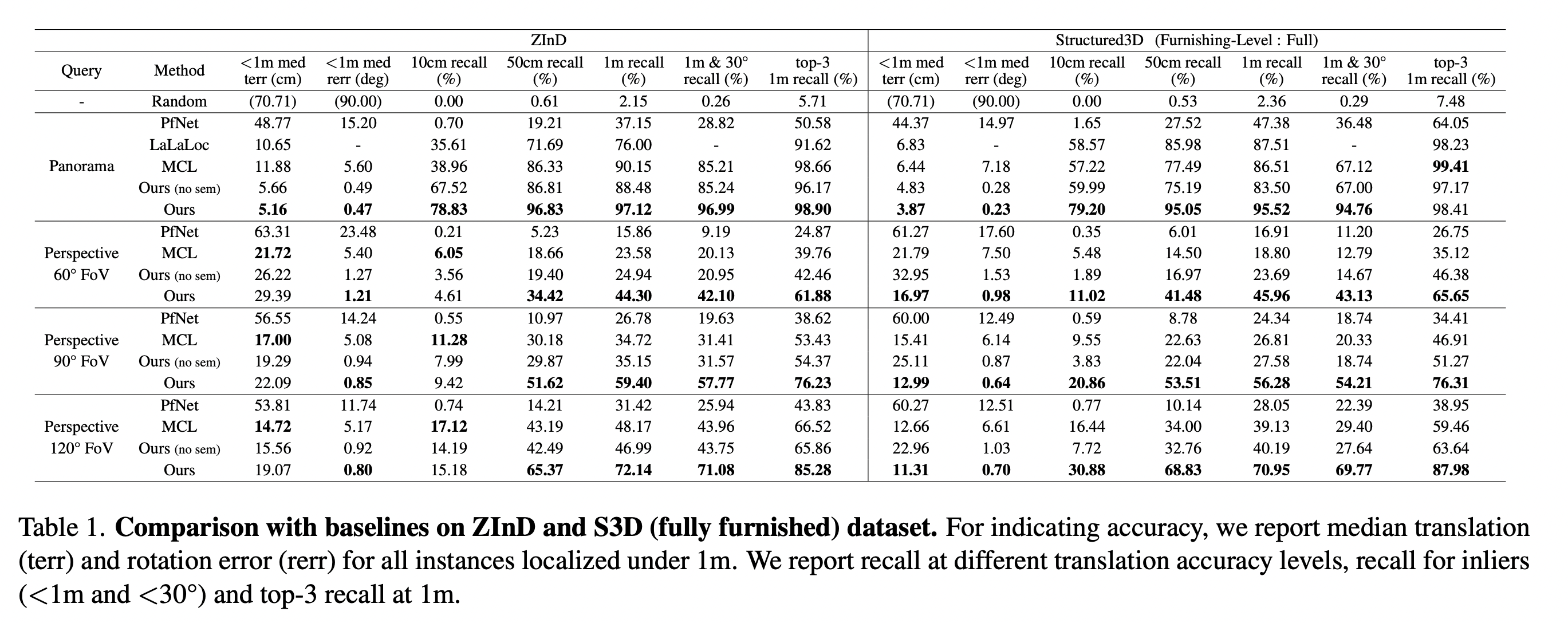
Experiments