Type I and Type II errors

제1종 오류와 제2종 오류는 가설 검정과 통계에서 중요한 개념이다.
제1종 오류와 제2종 오류를 이해하는 것은 실험 설계와 결과 해석에 있어 중요하다.
연구자들은 자신이 연구하는 특정 분야의 맥락에 따라 거짓 양성과 거짓 음성의 위험을 균형 있게 조절하여 연구하여야 한다.

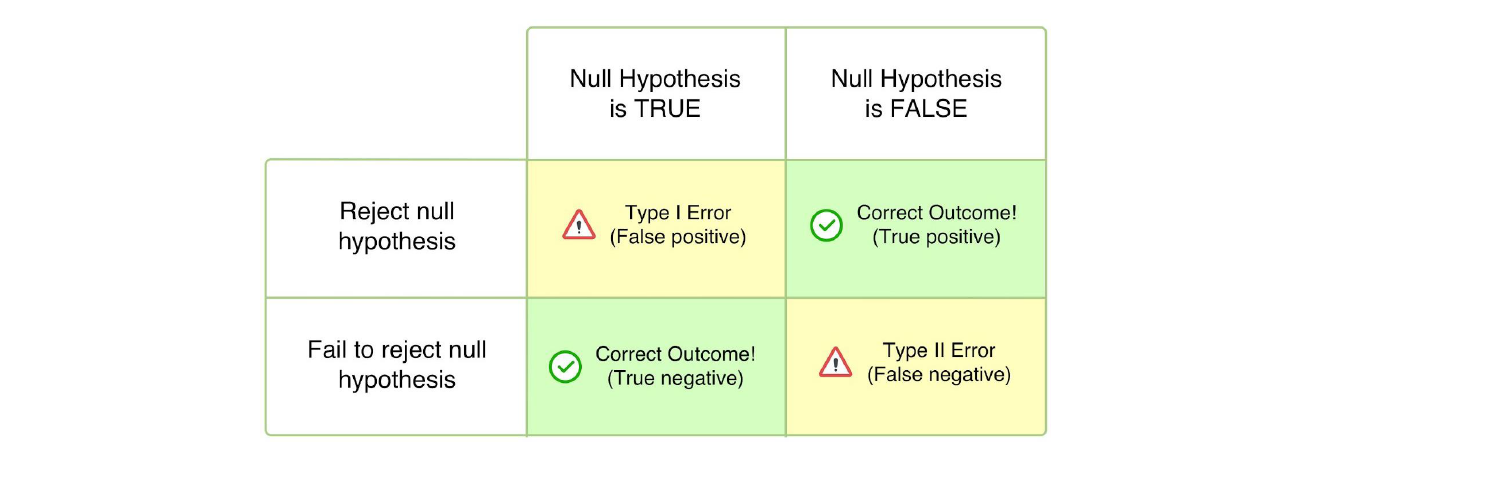
Type I error

• 정의: 제1종 오류는 귀무 가설(H0)이 참일 때, 이를 잘못 기각하는 오류이다. 이는 "false positive" or "alpha error"라고도 한다.

• 유의 수준 (α): 제1종 오류를 범할 확률은 α로 표시한다. 이 값은 테스트 전에 선택되며 귀무 가설을 기각하는 임계값을 나타낸다. 일반적인 α 값은 0.05, 0.01, 또는 0.10이다.

• 예시: 의료 테스트

• 시나리오: 새로운 질병 진단 테스트.

• 귀무 가설 (H0): 환자는 질병이 없다.

• 대립 가설 (H1): 환자는 질병이 있다.

• 제1종 오류: 테스트 결과 환자가 질병이 있다고 나타났지만, 실제로는 그렇지 않은 경우이다. 이는 불필요한 치료로 이어질 수 있으며, 환자에게 스트레스와 잠재적인 부작용을 초래할 수 있다.

• 결과: 불필요한 치료, 스트레스, 의료 비용.

Type II error

• 정의: 제2종 오류는 귀무 가설(H0)이 거짓일 때, 이를 기각하지 못하는 오류이다. 이는 "거짓 음성" 또는 "베타 오류"라고도 한다.

• power of the test (1 - β): 제2종 오류를 범하지 않을 확률을 power of the test이라고 한다. 제2종 오류를 범할 확률은 β로 표시된다.

• 예시: 의료 테스트

• 시나리오: 새로운 질병 진단 테스트.

• 귀무 가설 (H0): 환자는 질병이 없다.

• 대립 가설 (H1): 환자는 질병이 있다.

• 제2종 오류: 테스트 결과 환자가 질병이 없다고 나타났지만, 실제로는 질병이 있는 경우이다. 이는 환자가 필요한 치료를 받지 못해 상태가 악화될 수 있다.

• 결과: 오진, 필요한 치료의 부족, 건강 상태 악화.

Example of Type I a& II Errors in a Fire Alarm System

Type I a& II Errors를 설명하는데 종종 사용되는 예시인 화재경보시스템 예시이다.

Type I Error (False Positive)

• 정의: 제1종 오류는 화재 경보 시스템이 화재가 없을 때(귀무 가설이 참일 때) 화재가 발생했다고 신호를 보내는 경우(귀무 가설을 기각하는 경우)
• 유의 수준 (α): 거짓 양성(제1종 오류)의 확률은 α로 표시된다.
• 예제:
  • 시나리오: 건물에 화재 경보 시스템이 설치되어 있다.
  • 귀무 가설 (H0): 건물에 화재가 없다.
  • 대립 가설 (H1): 건물에 화재가 있다.
  • 제1종 오류: 실제로 화재가 없는데 화재 경보가 울리는 경우이다. 이는 요리 중 연기, 샤워에서 나오는 증기, 경보 시스템의 오작동 등으로 인해 발생할 수 있다.
• 결과:
  • 건물 대피.
  • 활동의 방해 가능성.
  • 불필요한 공황.
  • 소방서 호출과 같은 거짓 경보와 관련된 잠재적 비용.

Type II Error (False Negative)

• 정의: 제2종 오류는 화재 경보 시스템이 화재가 있을 때(귀무 가설을 기각하지 못할 때) 화재를 알리지 못하는 경우를 의미한다(귀무 가설이 거짓임).
• power of the test (1 - β): 화재가 있을 때 이를 올바르게 감지할 확률을 power of the test이라고 하며, 거짓 음성(제2종 오류)의 확률은 β로 표시된다.
• 예제:
  • 시나리오: 건물에 화재 경보 시스템이 설치되어 있다.
  • 귀무 가설 (H0): 건물에 화재가 없다.
  • 대립 가설 (H1): 건물에 화재가 있다.
  • 제2종 오류: 실제로 화재가 있는데도 화재 경보가 울리지 않는 경우이다. 이는 경보 시스템의 배터리 방전이나 센서의 결함 등으로 인해 발생할 수 있다.
• 결과:
  • 화재가 확산되어 건물에 심각한 손상을 입히고 생명의 손실을 초래할 수 있다.
  • 대피가 지연되어 거주자의 위험이 증가한다.
  • 재산 손상 및 잠재적인 법적 책임으로 인해 비용이 증가한다.

Type I and Type II Errors 정리

• 제1종 오류와 제2종 오류는 서로 반비례 관계에 있다. 즉, 한 유형의 오류 확률을 줄이면 다른 유형의 오류 확률이 증가하는 경우가 많다. 이 관계는 가설 검정의 근본적인 측면이며, 유의 수준(α), 검정력(power of the test;1 - β), 표본 크기, 그리고 실제 효과 크기에 의해 영향을 받는다.

제1종 오류 (거짓 양성)

• 정의: 귀무 가설(H0)이 참일 때, 이를 잘못 기각하는 경우이다.
• 확률 (α): 유의 수준으로, 제1종 오류를 범할 확률이다. 연구자들은 테스트를 수행하기 전에 이 값을 설정한다 (일반적으로 0.05, 0.01 등).

제2종 오류 (거짓 음성)

• 정의: 귀무 가설(H0)이 거짓일 때, 이를 기각하지 않는 경우이다.
• 확률 (β): 제2종 오류를 범할 확률이다. 검정력(power of the test;1 - β)은 거짓 귀무 가설을 올바르게 기각할 확률이다.

Trade-off Between Type I and Type II Errors

1. 유의 수준 (α)와 검정력 (1 - β):

• 유의 수준(α)을 낮추어(까다롭게 하여) 제1종 오류의 확률을 줄이면 테스트가 더 엄격해져 실제 효과를 감지하기 어려워지므로 제2종 오류(β)의 확률이 증가할 수 있다.
• 반대로, α를 높이면 β가 줄어들어 검정력이 증가하지만 제1종 오류의 위험도 증가한다.

2. 표본 크기:

• 표본 크기를 늘리면 α와 β가 모두 줄어들어 실제 효과를 감지할 수 있는 검정의 능력이 향상되고 제1종 오류와 제2종 오류의 발생 가능성이 줄어든다.
• 더 큰 표본은 모집단에 대한 더 많은 정보를 제공하여 귀무 가설과 대립 가설을 구분하기 쉽게 만든다.

3. 효과 크기:

• 효과 크기가 클수록(모집단 간의 실제 차이) 실제 효과를 감지하기 쉬워져 β가 줄어든다.
• 효과 크기가 작으면 β가 높아져 실제 차이를 감지하기 어려워지고, 제2종 오류가 증가할 수 있다.

Practical Example: Medical Testing

• 시나리오: 새로운 질병 진단 테스트가 평가되고 있다.
• 귀무 가설 ($H_0$): 환자가 질병이 없다.
• 대립 가설 ($H_1$): 환자가 질병이 있다.
• 제1종 오류 (거짓 양성):
  • 테스트가 환자가 질병이 있다고 나타내지만 실제로는 그렇지 않은 경우.
  • 결과: 불필요한 치료, 증가된 의료 비용, 환자의 불안.
• 제2종 오류 (거짓 음성):
  • 테스트가 환자가 질병이 없다고 나타내지만 실제로는 질병이 있는 경우.
  • 결과: 진단 누락, 치료 부족, 질병의 진행.

의료 테스트에서 오류의 균형 맞추기

• 의료 테스트에서 제1종 오류와 제2종 오류 간의 균형은 질병의 심각성과 잘못된 진단의 결과에 따라 달라진다.
• 제1종 오류의 위험이 높은 경우:
  • 더 엄격한 기준 (낮은 $\alpha$).
  • 거짓 양성이 거짓 음성보다 덜 해로울 때 수용 가능.
  • 예: 심각하지만 치료 가능한 질병의 선별 검사.
• 제2종 오류의 위험이 높은 경우:
  • 더 관대한 기준 (높은 $\alpha$).
  • 진단 누락이 더 해로울 때 수용 가능.
  • 예: 거짓 음성의 비용이 매우 높은 확인 검사.

Summary

제1종 오류와 제2종 오류 간의 관계는 실험 설계와 결과 해석에서 신중한 고려가 필요하다. 연구자들은 거짓 양성(제1종 오류)을 피하려는 필요성과 실제 효과를 감지하려는 필요성(제2종 오류 최소화)을 균형 있게 맞춰야 하며, 종종 최적의 균형을 이루기 위해 표본 크기와 유의 수준을 조정한다.