이번 포스트에서는

• 유의성 검사 및 가설 검정 개념을 다룹니다.
• 영가설과 대립가설, 검사 통계량 및 다양한 분포(정규 분포, t-분포, 카이제곱 분포, F-분포)를 설명합니다.
• 다양한 통계 검사를 위한 임계값, 유의 수준 및 p-값을 논의합니다.

Significant Test(유의성 검정)

유의성 검정은 표본 데이터를 기반으로 모집단 모수에 대한 귀무 가설을 기각할 수 있는 충분한 증거가 있는지를 판단하기 위해 사용되는 통계적 테스트이다.

필요성

• 이러한 테스트는 데이터에서 관찰된 효과의 신뢰성을 평가하는 데 필수적이다.
• 관찰된 현상이 우연에 의한 것인지, 또는 실제로 실질적인 의미가 있는지 평가한다. 이는 데이터에서 관찰된 효과의 신뢰성을 판단하는데 필요하다.

$H_0$ vs. $H_1$

귀무 가설 ($H_0$):

정의: 두 측정된 현상 간에 관계가 없거나 그룹 간에 연관성이 없다는 일반적인 진술 또는 기본 입장이다.
예시: "남성과 여성의 평균 키에 차이가 없다"는 주장.
목표: 일반적으로 연구자는 연구를 통해 귀무 가설이 기각되기를 희망한다.

대립 가설 ($H_1$):

정의: 연구자가 입증하고자 하는 주장으로, 귀무 가설과 반대되는 진술이다.
예시: "남성이 평균적으로 여성보다 키가 크다"는 주장.
목표: 연구자는 연구를 통해 대립 가설이 채택되기를 희망한다.

-> 귀무 가설은 일반적으로 "차이가 없다" 또는 "효과가 없다"가 기본 입장인 반면, 대립 가설은 연구자가 증명하고자 하는 바를 나타낸다.

예시

연구자 A : 가구 소득이 전년 대비 크게 증가했다고 주장
연구자 B : 가구 소득의 증가가 단지 우연의 일치일 뿐 실제로 소득이 증가하지 않았다고 주장

이때,
귀무가설($H_0$) : 전년도와 비교하여 가구 소득이 실제로 증가하지 않았다는 주장.
대립 가설($H_1$) : 전년도와 비교하여 가구 소득이 실제로 증가했다는 주장.

Test Statistic(검정 통계량)

정의: 가설 검정 중에 샘플 데이터로부터 계산된 수치 값
이 값은 귀무 가설에 명시된 내용으로부터 표본 증거가 얼마나 벗어났는지를 평가하는 데 사용됩니다.

역할: 귀무 가설에 명시된 내용으로부터 표본 증거가 얼마나 벗어났는지를 평가하여 귀무 가설을 기각할지 여부(타당성)를 결정하는 중요한 역할을 한다.

Test Statistic은 귀무 가설이 참일 때 알려진 확률 분포를 따른다. 연구자는 이 Test Statistic 기반하여 귀무 가설을 기각할지 결정한다.
가설 검정에서 일반적으로 사용되는 분포로는 아래 4가지 등등이 있다.

• 정규 분포(Normal distribution)
• t-분포(t-distribution)
• 카이제곱 분포(Chi-square distribution)
• F-분포(F-distribution)

Types of test statistics

1. Z-점수 (Z-score in Normal Distribution)

• 정의: Z-점수는 특정 값이 평균에서 얼마나 떨어져 있는지를 표준 편차 단위로 나타낸 값이다.
• 사용 상황:
  • 표본 크기가 클 때 사용
  • 모집단의 표준 편차($\sigma$)를 알고 있을 때 사용
  • Z-점수는 정규 분포를 따른다.
• 공식:
  $Z = \frac{X - \mu}{\sigma / \sqrt(n)}$
  여기서 $X$는 데이터 값, $\mu$는 모평균, $\sigma$는 모표준 편차, $\sigma / \sqrt(n)$는 $SEM$(표준 오차)

2. T-점수 (T-score in t-Distribution)

• 정의: T-점수는 Z-점수와 유사하지만, 표본 크기가 작거나 모집단의 표준 편차를 모를 때 사용
• 사용 상황:
  • 표본 크기가 작을 때 사용
  • 모집단의 표준 편차를 모를 때 사용
  • T-점수는 t-분포를 따른다.
• 공식:
  $T = \frac{\bar{X} - \mu}{s / \sqrt{n}}$
  여기서 $\bar{X}$는 표본 평균, $\mu$는 모평균, s는 표본 표준 편차, n은 표본 크기
• Z-점수와 T-점수 모두 모평균과 표본집단의 크기를 알아여 된다.
• Z-점수는 데이터 값(혹은 표본평균)과 모표준편차를 알아야 되고 T-점수 는 표본평균과 표본표준편차를 알아야 한다.

Z-점수 예시

예를 들어, 모집단의 평균 키가 170cm이고 표준 편차가 10cm인 경우, 표본 크기 $n$이 25인 표본의 평균 키가 175cm라면, Z-점수는 다음과 같이 계산된다.
$Z = \frac{175 - 170}{10 / \sqrt{25}} = \frac{5}{10 / 5} = \frac{5}{2} = 2.5$

T-점수 예시

예를 들어, 모집단의 평균 키가 170cm이지만 모집단의 표준 편차를 모르는 경우, 표본 크기 $n$이 25인 표본의 평균 키가 175cm이고 표본 표준 편차가 12cm라면, T-점수는 다음과 같이 계산됩니다:
$t = \frac{175 - 170}{12 / \sqrt{25}} = \frac{5}{12 / 5} = \frac{5}{2.4} \approx 2.08$

각각의 분포를 따르기 때문에 절대적인 상수간 비교는 불가능.

죄송합니다. 다시 확인해본 결과, PDF의 8페이지는 카이제곱 분포와 F-분포에 대해 설명하고 있습니다. 아래에 각 분포에 대한 내용을 자세히 설명드리겠습니다.

3. 카이제곱 분포 (Chi-Square Distribution)

• 독립성 검정 또는 적합도 검정에서 자주 사용되며, 카테고리 별로 관찰된 빈도를 기대 빈도와 비교한다.
• 공식:
  $\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}$ 여기서 $O$와 $E$는 각각 관찰된 빈도(observed frequency)와 기대 빈도(expected frequency)를 나타낸다. 각각 카테고리 $i$에서의 비교값들을 합산하여 계산한다.

4. 분산 분석(ANOVA)에서 F-분포 (F-Distribution)

• 세 개 이상의 그룹의 분산을 비교하여 적어도 하나의 표본 평균이 다른 것들과 다른지 확인하는 데 사용
• 공식:
  $F = \frac{\text{Between-group variance}}{\text{Within-group variance}}$ ( $F = \frac{\text{그룹 간 분산}}{\text{그룹 내 분산}}$)

요약

• 카이제곱 분포는 범주형 데이터의 적합도 검정이나 독립성 검정에 사용되며, 관찰 빈도와 기대 빈도의 차이를 평가
• F-분포는 하나의 그룹에서 사용하는 카이제곱 분포과 달리 여러 그룹 간의 분산을 비교하여 사용

Normal Distribution

정규 분포는 가우시안 분포라고도 불리며, 통계에서 가장 기본적인 확률 분포 중 하나이다. 이 분포는 대칭적이고 종 모양의 곡선으로 특징지어지며, 평균, 중앙값, 최빈값이 모두 동일하다.

• 형태: 평균을 기준으로 대칭

• 매개변수: 평균($\mu$)과 표준 편차($\sigma$) 두 가지 매개변수로 정의된다.

• 공식: 확률 밀도 함수(PDF)로 그림을 그리고, 공식은 아래와 같다.
  $f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}$

• 용도: 정규 분포는 hypothesis testing(가설 검정), regression analysis(회귀 분석), Central Limit Theorem(중앙 극한 정리) 등 많은 분야에서 사용된다. 중앙 극한 정리는 많은 수의 랜덤 변수의 합이 그 분포와 상관없이 정규 분포에 가까워진다는 것이다.

아래는 Normal Distribution들의 그래프 개형이다.

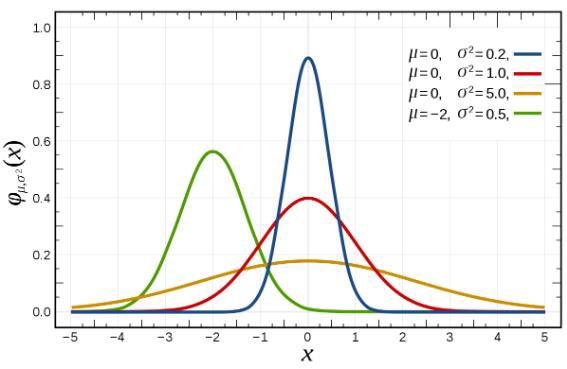
그래프의 개형을 결정짓는 파라미터는 평균($\mu$)과 표준 편차($\sigma$)이다.

• $\mu$ = 0, $\sigma$ = 1 일때 Standard Normal Distribution

t-Distribution

t-분포, 또는 스튜던트의 t-분포는 정규 분포와 유사하지만 뚱뚱한 꼬리(fatter tails)를 가진다. 주로 표본 크기가 작거나 모집단의 표준 편차를 알 수 없을 때 사용된다.

• 형태: 정규 분포와 마찬가지로 대칭적이지만, 꼬리가 더 두꺼워서 꼬리 부분에 더 많은 확률을 가진다(샘플이 작아 모수의 모양을 정확히 알 수 없으므로).
• 매개변수: 자유도(df)라는 하나의 매개변수로 정의된다.
• 공식: $f(t \mid \text{df}) = \frac{\Gamma\left(\frac{\text{df}+1}{2}\right)}{\sqrt{\text{df}\pi} \Gamma\left(\frac{\text{df}}{2}\right)} \left(1 + \frac{t^2}{\text{df}}\right)^{-\frac{\text{df}+1}{2}}$

여기서:

• $t$는 T-점수

• $\text{df}$는 자유도 (degrees of freedom)

• $\Gamma$는 감마 함수

• 용도: 신뢰성을 높이기 위해서는 많은 표본을 얻어야 하지만, 현실적으로는 시간과 비용의 제한으로 많은 표본을 얻을 수 없는 경우가 많다. 이러한 경우, 예측 범위가 정규 분포보다 더 넓은 t-분포를 사용한다. 이는 특히 표본 크기가 작은 상황에서, 모집단의 표준 편차를 모를 때 신뢰 구간 계산 및 가설 검정에 사용된다.

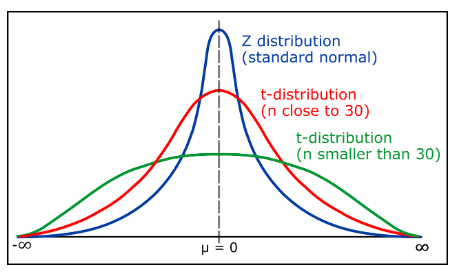
샘플의 수가 늘어날수록, 그래프의 개형은 Normal Distribution에 가까워진다.

자유도 (degrees of freedom)?

변수가 n개면 n-1로 표현이 된다.
자유도는 통계적 분석에서 특정 선택의 자유를 나타내며, 아래 예시에서는 7개의 모자 중 6일 동안 선택할 수 있는 자유도가 있었음을 나타낸다.

당신은 일주일 동안 매일 다른 모자를 쓰고 싶다.

• 당신은 7개의 모자를 가지고 있다.
• 첫째 날에는 7개의 모자 중 아무거나 쓸 수 있다. 둘째 날에는 남은 6개의 모자 중에서 선택할 수 있고, 셋째 날에는 5개의 모자 중에서 선택할 수 있다.
• ...
• 여섯째 날에는 아직 쓰지 않은 두 개의 모자 중 하나를 선택할 수 있다.
• 그러나 일곱째 날에는 더 이상 선택할 수 있는 모자가 없으며, 마지막 남은 모자를 써야 한다.
• 즉, 6일 동안 선택할 수 있는 '모자'의 자유도가 있었다 (7-1).

Chi-Square Distribution

카이제곱 분포는 독립적인 표준 정규 변수를 제곱하여 얻어지는 비대칭 분포이다. 이 분포는 가설 검정, 특히 독립성 검정과 적합도 검정에서 매우 중요하다.

• 형태: 비대칭적이며, 0에서 시작하여 오른쪽으로 확장되며, 자유도가 증가함에 따라 더 대칭적으로 변한다.
• 매개변수: 자유도(df)라는 하나의 매개변수로 정의된다.
• 공식:
  $f(x \mid \text{df}) = \frac{x^{(\text{df}/2)-1} e^{-x/2}}{2^{\text{df}/2} \Gamma(\text{df}/2)}$

여기서:

• $x$는 카이제곱 값

• $\text{df}$는 자유도 (degrees of freedom)

• $\Gamma$는 감마 함수

• 용도: 각 범주의 '관찰 빈도'와 '기대 빈도' 사이의 차이를 살펴봄으로써 주어진 데이터가 특정 확률 모델에서 얻어졌는지를 검정하는 데 사용된다.

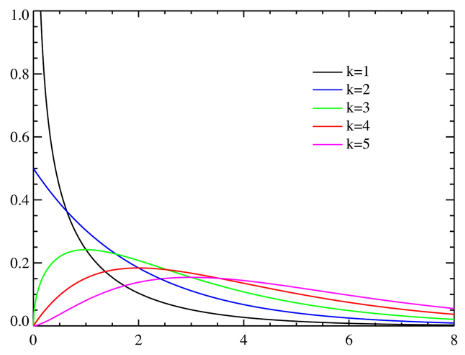
k = degrees of freedom

F-Distribution

F-Distribution은 주로 분산 분석(ANOVA)에서 사용된다. 이는 두 분산의 비율을 비교할 때, 예를 들어 ANOVA나 회귀 분석에서 발생합니다.

• 형태: 비대칭적이며, 카이제곱 분포와 유사하지만 두 개의 다른 자유도에 의해 형태가 결정됩니다.
• 매개변수: 분자의 자유도($\text{df}_1$)와 분모의 자유도($\text{df}_2$)두 개의 매개변수로 정의된다.
• 공식:
  $f(x \mid \text{df}_1, \text{df}_2) = \sqrt{\frac{(\text{df}_1 x)^{\text{df}_1} \text{df}_2^{\text{df}_2}}{(\text{df}_1 x + \text{df}_2)^{\text{df}_1 + \text{df}_2}}} \Big/ \left( x \cdot B\left(\frac{\text{df}_1}{2}, \frac{\text{df}_2}{2}\right) \right)$
• 용도: 주로 분산 분석(ANOVA)에서 여러 그룹 간의 분산을 비교하고, 회귀 분석에서 예측 변수의 유의성을 검정하는 데 사용된다.

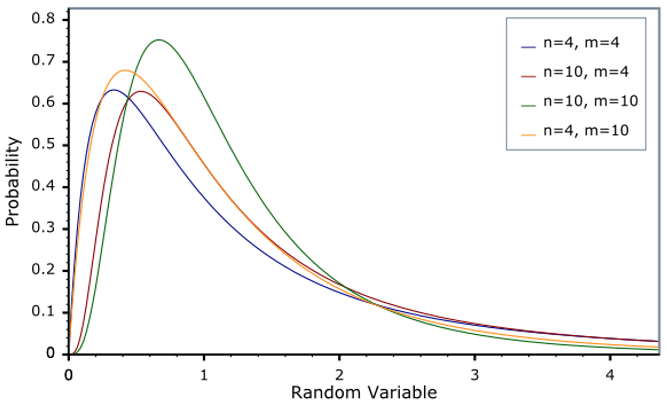
Test Statistic

• 결과 결정

  • 검정 통계량을 계산한 후, 선택된 유의 수준(α)을 고려하여 관련 분포의 임계값과 비교한다.
  • 검정 통계량이 임계값을 초과하면, 귀무 가설을 기각하며 이는 관찰된 효과(주장)가 통계적으로 유의미함을 시사한다.
  • 이 과정은 과학적 가설의 타당성을 결정하는 데 필수적이다.

• critical value(임계값)

  • 주어진 유의 수준에서 귀무 가설을 받아들일지 기각할지를 결정할 때 기준이 되는 값.

• Significance Level : 유의 수준 (α)

  • 연구자가 선택한 기준 값으로, p-value와 비교된다.
  • critical value가 그래프에서 일종의 x값이고, Significance Level은 어떤 밀도함수의 면적의 값으로 이해하자.
  • 이 값은 종종 0.05로 설정된다.
  • p-value가 α(0.05)보다 작으면, 귀무 가설을 기각한다.(대립가설 채택)

• p-value

  • p-값은 실제 데이터로부터 계산된 값
  • 귀무 가설이 맞다는 가정 하에, 실제로 관찰된 결과와 같거나 더 극단적인 결과를 얻을 확률.
  • p-value가 작을수록 관찰된 데이터가 귀무 가설 하에서는 발생하기 어려움을 나타낸다.(귀무가설이 아닌, 실험으로 주장하는 바가 맞다는 것)

이 페이지는 통계적 가설 검정에서 중요한 개념인 임계값, 유의 수준, 그리고 p-값에 대해 설명하고 있습니다. 유의 수준(α)은 연구자가 설정한 기준값으로, p-값과 비교하여 귀무 가설을 기각할지 결정합니다. p-값은 귀무 가설 하에서 관찰된 데이터가 얼마나 극단적인지를 나타내는 확률로, p-값이 작을수록 귀무 가설을 기각할 가능성이 높아집니다.

Z-test

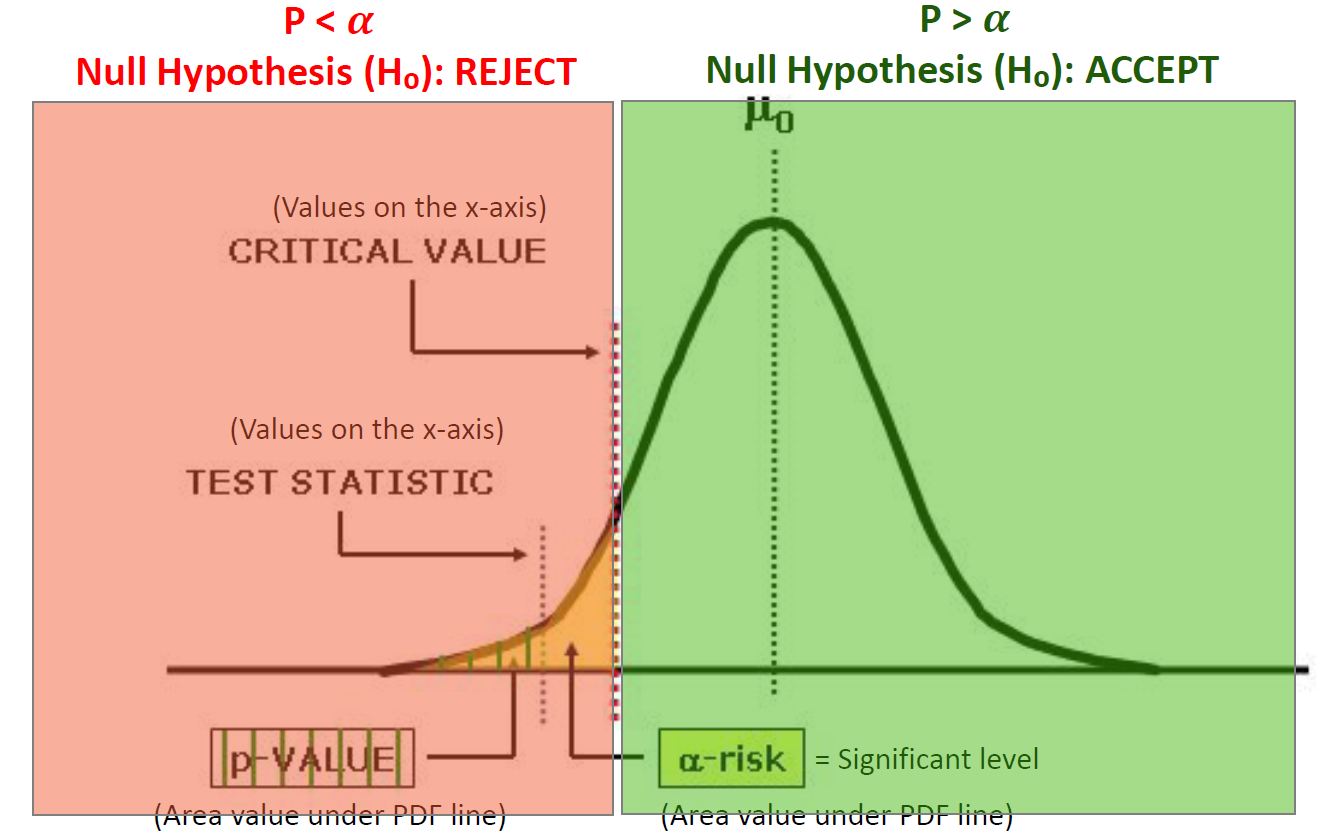
critical value : Z값
Significance Level : 노란색 면적
p-value : 초록 빗금 면적
p-value와 Significance Level를 비교하여 귀무가설을 기각할지 정한다.

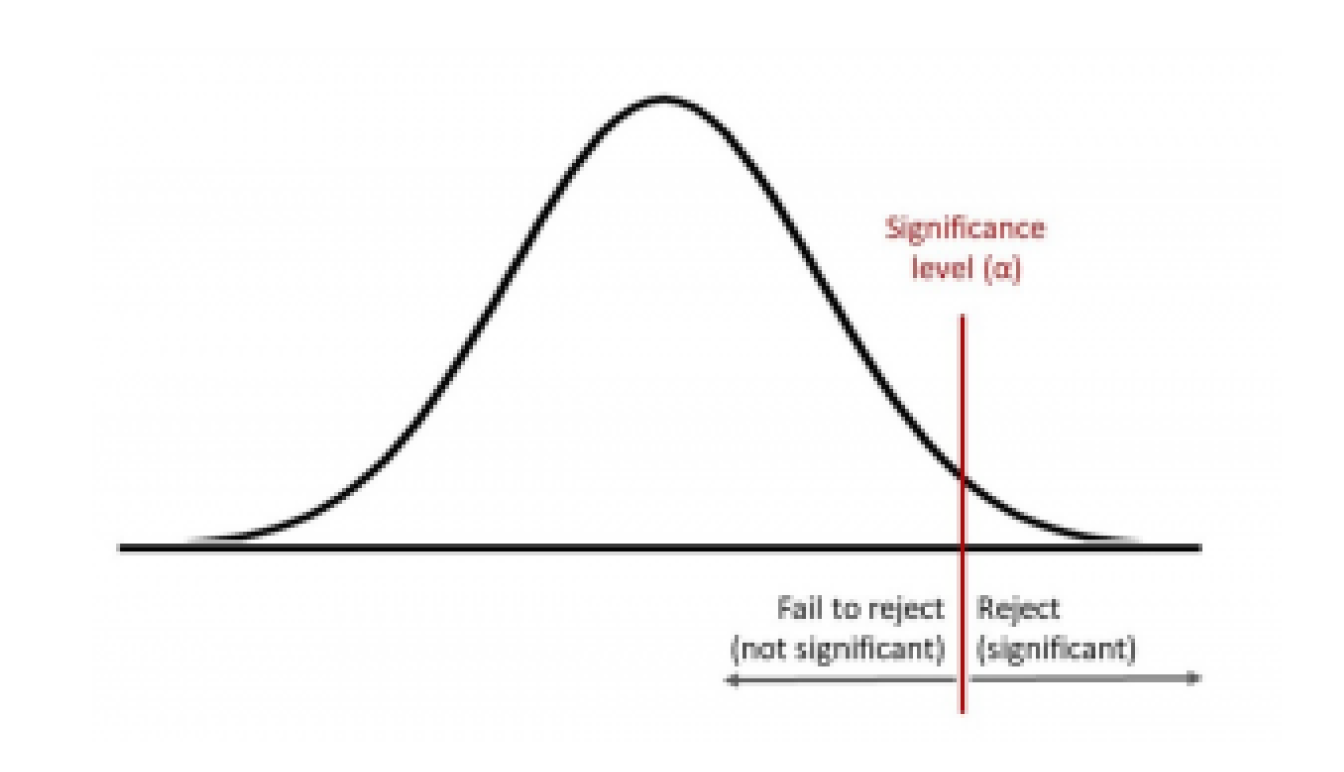
one tail만 볼 경우 반대의 상황도 있을 수 있는데, p-value와 Significance Level을 비교할 경우 부등호의 방향이 바뀌지는 않는다.
하지만 x축 값인 critical value와 test statistic을 비교할 경우 부등호의 방향이 바뀜에 주의하자.

Z-test in Standard Normal Distribution

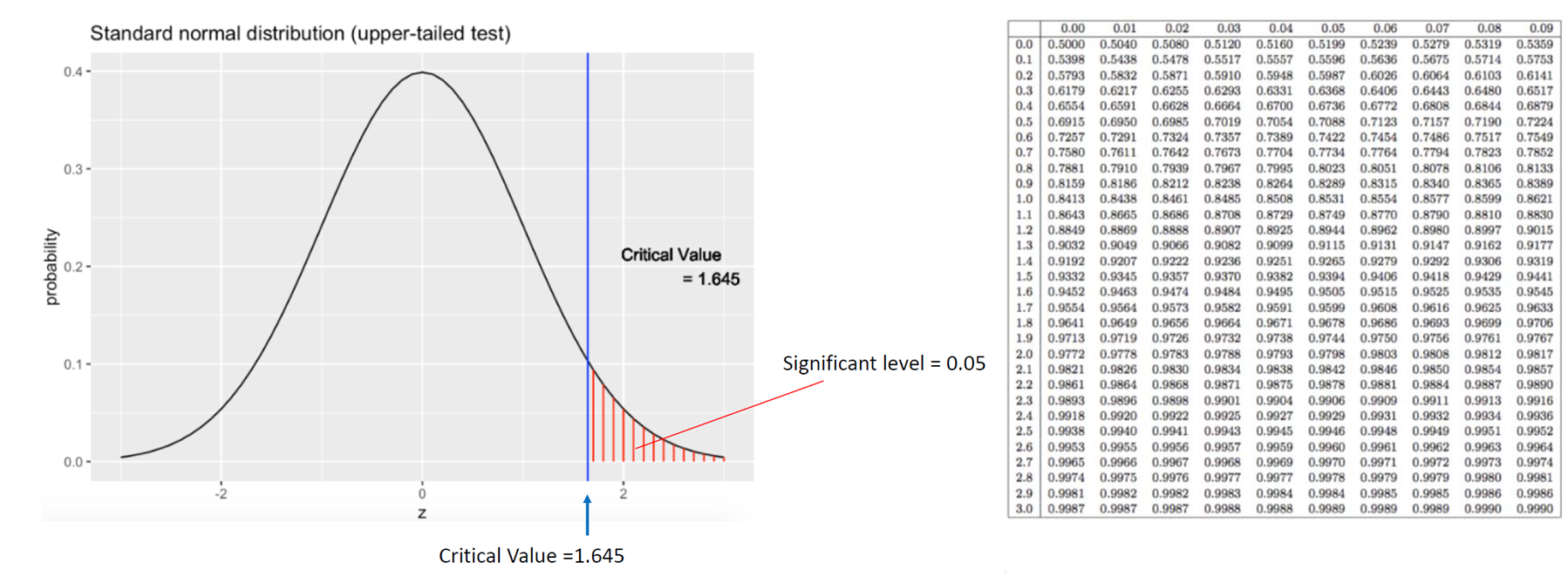
Standard Normal Distribution의 경우에는 이미 도표로 계산된 결과가 나와있기 때문에 계산하기 쉽다.

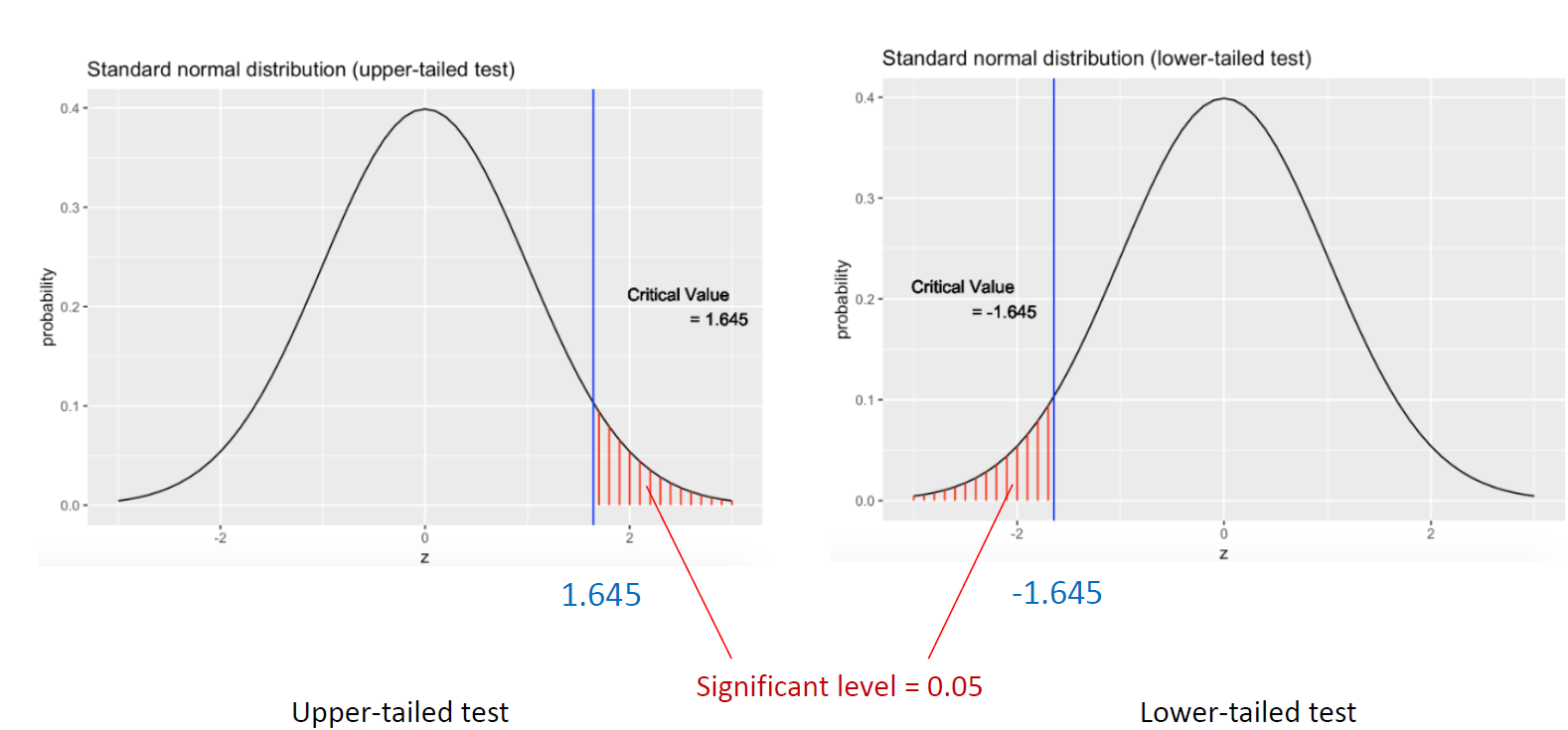
upper tail과 lower tail의 면적이 같음을 확인할 수 있다.

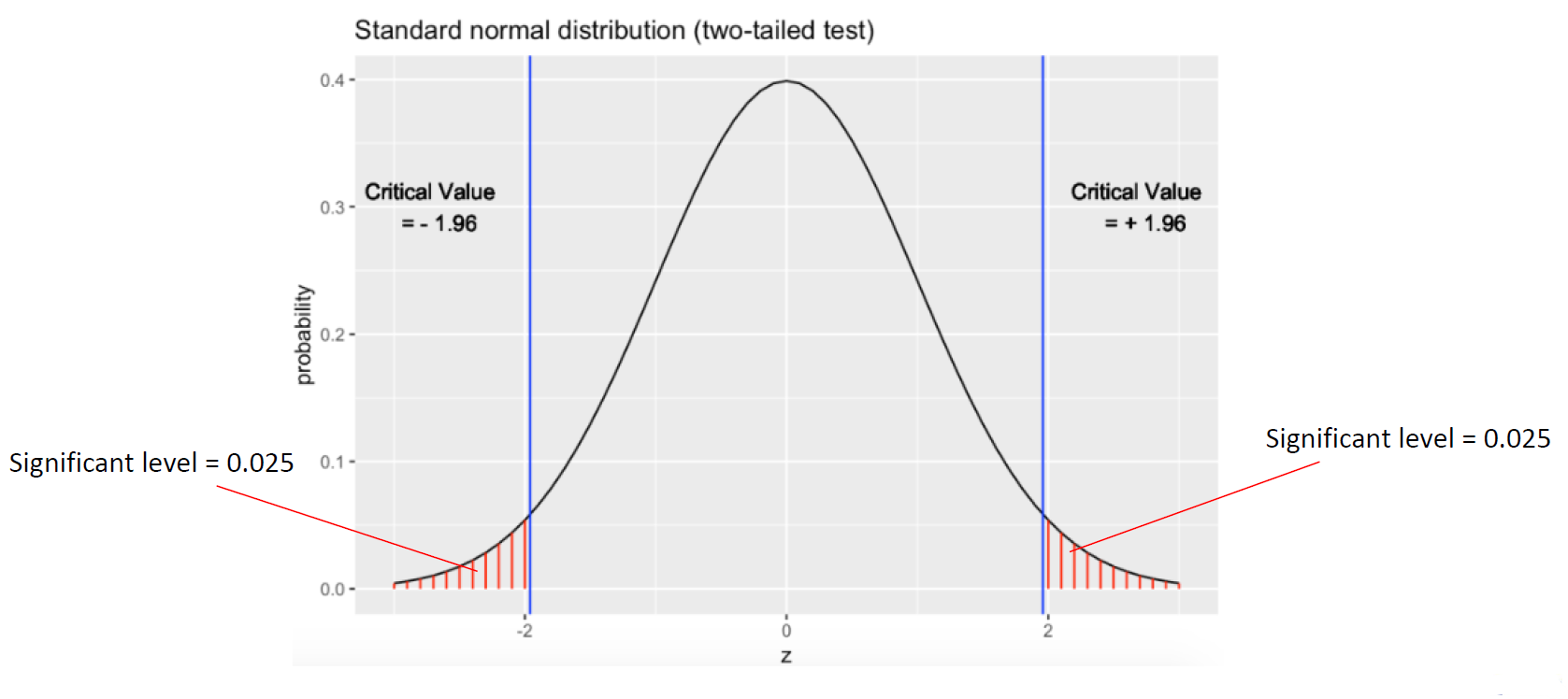
two tail의 경우에는 Significance Level의 값이 절반으로 나누어짐을 생각할 수 있다.

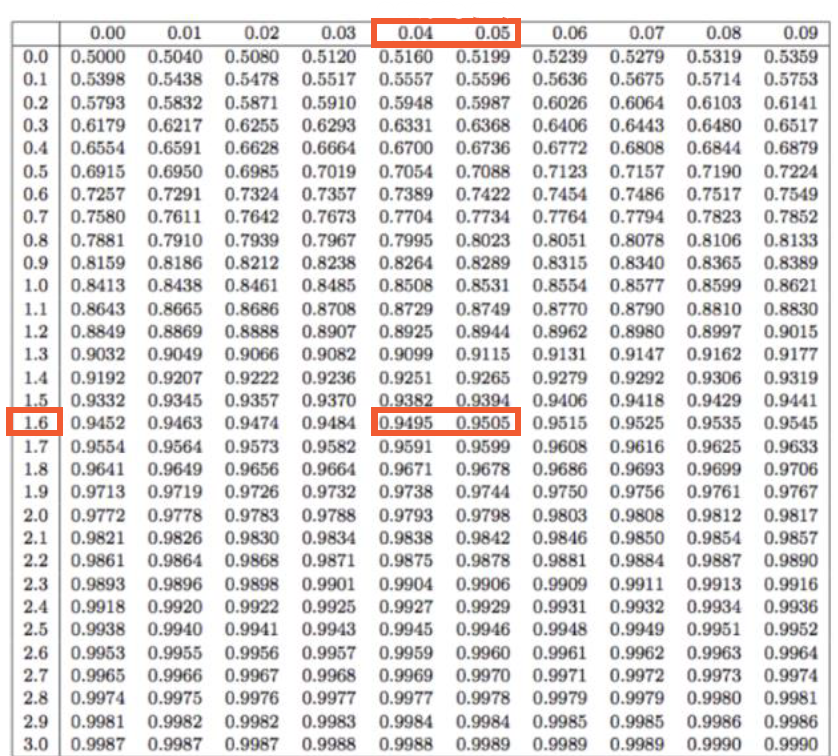
Cumulative distribution table을 활용하여 critical value 값을 구할 수 있다.
CDF(z) = 0.95
Z = the middle value between 1.64 and 1.65
=> Critical value = 1.645
CDF(z) = 0.05
Z = the middle value between -1.64 and -1.65
=> Critical value = -1.645
대칭형태이기 때문에 0.95의 값을 구해서 -값을 구하면 된다.