1. Z-test

Eg1.

웹사이트를 관리하고 있으며, 새로운 버전의 웹페이지가 사용자가 페이지에 머무는 평균 시간을 증가시키는지 알고 싶다고 가정해자. 과거 데이터에 따르면, 사용자는 평균적으로 200초 동안 머물며, 표준 편차는 40초이다. 새로운 페이지에서 100명의 사용자를 샘플링한 결과, 평균 210초 동안 머물렀다.(양측 5% 유의 수준을 고려한다.)

Answer

1. 가설 설정:

• 귀무가설(H0): 평균 시간 = 200초.
• 대립가설(H1): 평균 시간 ≠ 200초.

2. Z-점수 계산:
   $Z = \frac{\bar{x} - \mu}{\frac{\sigma}{\sqrt{n}}}$

여기서, $\bar{x} = 210$초, $\mu = 200$초, $\sigma = 40$초, $n = 100$이다.

$Z = \frac{210 - 200}{\frac{40}{\sqrt{100}}} = \frac{10}{4} = 2.5$

3. 유의성 판단:
   

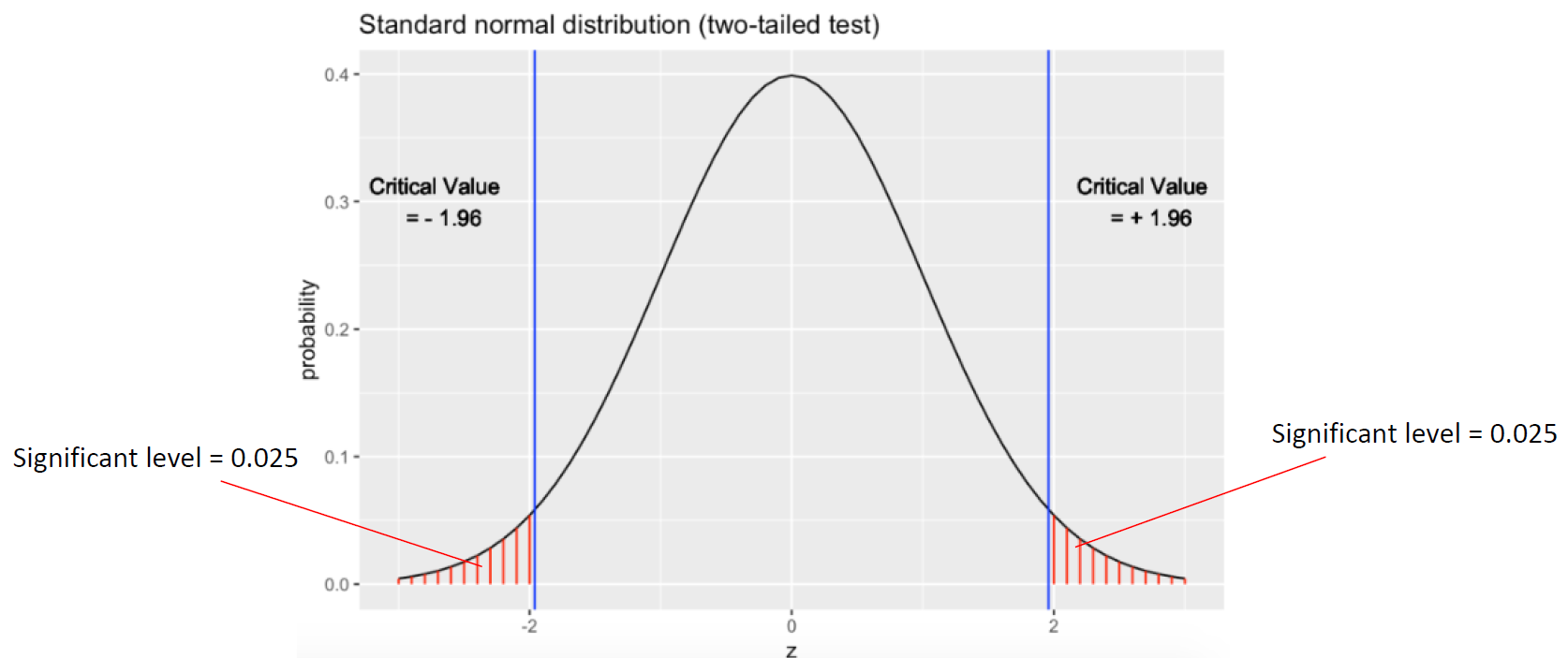
Z-표에서 Z-score를 임계값과 비교한다. 만약 Z = 2.5이고, 5% 유의 수준(양측 검정)을 사용하는 경우, 임계 Z-값은 ±1.96이다. 2.5 > 1.96이므로, 귀무가설을 기각하고 새로운 페이지가 사용자가 머무는 시간을 증가시킨다고 결론 내릴 수 있다.

Eg2.

한 회사가 자사의 전구 수명이 평균 1200시간이며 표준 편차가 200시간이라고 주장한다. 50개의 전구를 테스트한 결과 평균 1150시간 동안 지속되었다.(양측 5% 유의 수준을 고려한다.)

Answer

문제 1)

1. 가설 설정:

   • 귀무가설 (H0): 평균 수명 = 1200시간.
   • 대립가설 (H1): 평균 수명 ≠ 1200시간.

2. Z-점수 계산:
   $Z = \frac{\bar{x} - \mu}{\frac{\sigma}{\sqrt{n}}}$

$\bar{x} = 1150$, $\mu = 1200$, $\sigma = 200$, $n = 50$

$Z = \frac{1150 - 1200}{\frac{200}{\sqrt{50}}}$

$Z = \frac{-50}{\frac{200}{7.071}}$

$Z = \frac{-50}{28.284}$

$Z \approx -1.77$

3. 해석:
   양측 5% 유의 수준에서 임계 Z-값은 ±1.96이다. -1.77은 -1.96과 1.96 사이에 있으므로, 귀무가설(H0)을 기각하지 않는다. 즉, 전구의 수명은 1200시간과 유의미하게 다르지 않는 것으로 볼 수 있다.

Eg3.

한 음료 회사는 자사의 소다 캔에 355 ml가 들어 있으며 표준 편차가 5 ml라고 주장한다36개의 캔을 샘플링한 결과 평균 350 ml가 들어 있었었다. 실제 내용물이 355 ml와 다른지 테스트해보자.(양측 5% 유의 수준을 고려한다.)

Answer

1. 가설 설정:

• 귀무가설(H0): 내용물 용량간 유의미한 차이가 없다.
• 대립가설(H1): 내용물 용량간 유의미한 차이가 있다.
  모 평균 : 355ml
  모 표준편차 : 5ml
  표본평균 : 350ml
  $Z = \frac{\bar{x} - \mu}{\frac{\sigma}{\sqrt{n}}}$

$Z = \frac{350 - 355}{\frac{5}{\sqrt{36}}} = \frac{-5}{\frac{5}{6}} = \frac{-5}{0.833} \approx -6.0$

임계 Z-값은 ±1.96이다. -6.0 < -1.96이므로 귀무가설($H_0$)을 기각한다. 내용물이 355 ml와 유의미하게 다르다.

2. T-test

Eg1.

한 학교가 한 학급의 30명의 학생들에게 새로운 교육 방법을 도입했다. 역사적 평균 시험 점수는 75점이고 표준 편차는 10점이다. 새로운 학급의 평균 점수는 80점이다.(양측 5% 유의 수준을 고려한다.)

Answer

1. 가설 설정:

• 귀무가설(H0): 평균 점수 = 75.
• 대립가설(H1): 평균 점수 ≠ 75.

2. T-점수 계산:
   $t = \frac{\bar{x} - \mu}{\frac{s}{\sqrt{n}}}$

여기서, $\bar{x} = 80$, $\mu = 75$, $s = 10$, $n = 30$이다.

$t = \frac{80 - 75}{\frac{10}{\sqrt{30}}} = \frac{5}{\frac{10}{\sqrt{30}}} = \frac{5}{1.83} \approx 2.73$

3. 유의성 판단:
   

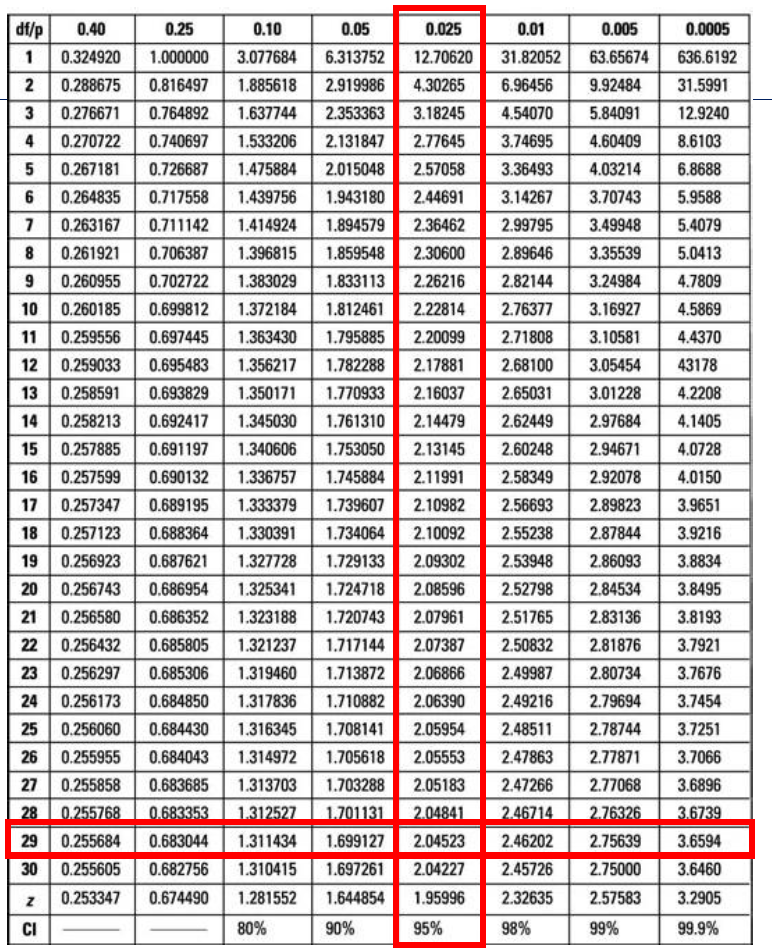
T-분포표에서 자유도 $n - 1$ (29)로 T-점수를 임계값과 비교한다. 유의 수준 5%일 때 임계 T-값이 약 2.045이고, $t = 2.73$이면 귀무가설을 기각한다. 즉, 새로운 방법이 점수를 향상시킨다고 결론 내릴 수 있다.

Eg2.

작은 클리닉에서 혈압 감소를 위한 새로운 다이어트 계획을 테스트한다. 10명의 환자가 등록되었고, 평균 감소는 8 mmHg, 표본 표준 편차는 4 mmHg이다. 예상 감소량은 5 mmHg이다.(양측 5% 유의 수준을 고려한다.)
해석: 예상 감소량은 기존의 감소량을 뜻한다. 기존의 평균 감소량(모평균)이 5mmHg라고 해석할 수 있다.

Answer

1. 가설 설정:

   • 귀무가설 (H0): 평균 감소량 = 5 mmHg.
   • 대립가설 (H1): 평균 감소량 ≠ 5 mmHg.

2. T-점수 계산:
   $t = \frac{\bar{x} - \mu}{\frac{s}{\sqrt{n}}}$

   여기서, $\bar{x} = 8$, $\mu = 5$, $s = 4$, $n = 10$이다.

   $t = \frac{8 - 5}{\frac{4}{\sqrt{10}}}$

   $t = \frac{3}{\frac{4}{3.162}}$

   $t = \frac{3}{1.264} \approx 2.37$

3. 해석:
   자유도 9에서 유의 수준 5% (양측 검정)일 때 임계 t-값은 약 2.262이다. 2.37 > 2.262이므로 귀무가설(H0)을 기각한다. 즉, 다이어트 계획이 유의미한 효과가 있음을 보여준다.

Eg3.

한 교사가 8명의 학생이 있는 반에 새로운 학습 방법을 도입했다. 평균 시험 점수 증가는 15점이며, 표본 표준 편차는 5점이다. 예상 증가는 10점이다. 새로운 방법이 효과적인지 테스트해보자
(양측 5% 유의 수준을 고려한다.)

Answer

1. 가설 설정:
   • 귀무가설 (H0): 새로운 방법은 기존과 차이가 없다.
   • 대립가설 (H1): 새로운 방법은 기존과 차이가 있다.(효과적이다)

모평균:10점
표본평균:15점
표본표준편차:5점
자유도:7

$t = \frac{\bar{x} - \mu}{\frac{s}{\sqrt{n}}}$

$t = \frac{15 - 10}{\frac{5}{\sqrt{8}}} = \frac{5}{\frac{5}{2.828}} = \frac{5}{1.77} \approx 2.82$

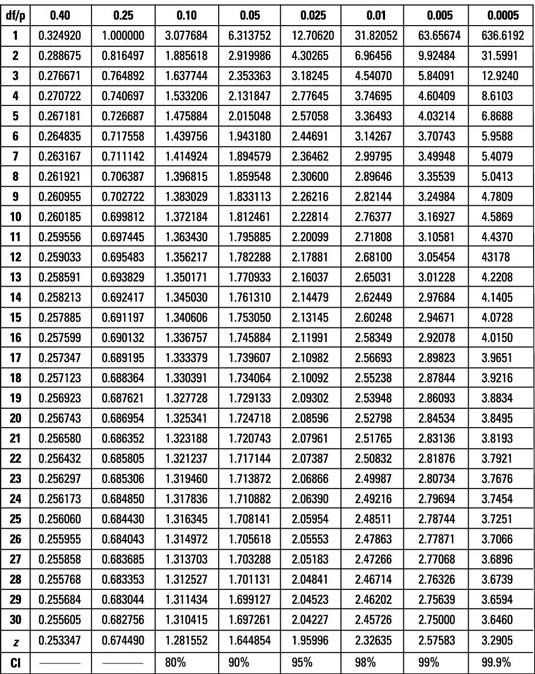
자유도 7에서 임계 t-값은 약 2.365이다. 2.82 > -2.365이므로 귀무가설($H_0$)을 기각한다. 방법은 효과적이다.

3. Chi-Square Test

여러 집단에 대해, 분산의 차이를 검정할때 주로 사용한다.

Eg1.

여섯 면이 있는 주사위가 공정한지 확인하고 싶다. 주사위를 60번 굴려서 다음과 같은 결과를 얻었다고 가정해보자.

• 1 : 5번
• 2 : 9번
• 3 : 11번
• 4 : 13번
• 5 : 12번
• 6 : 10번
  (한쪽의 5% 유의 수준을 고려)

Answer

1. 기대 빈도:
   공정한 주사위의 경우 각 면의 기대 빈도는 10번이다 (60 / 6).

   각 면에 대해 계산한 후 합산한다:
   $\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}$
   여기서, $O_i$ = 관측 빈도, $E_i$ = 기대 빈도 (10).

   $\chi^2 = \frac{(5 - 10)^2}{10} + \frac{(9 - 10)^2}{10} + \frac{(11 - 10)^2}{10} + \frac{(13 - 10)^2}{10} + \frac{(12 - 10)^2}{10} + \frac{(10 - 10)^2}{10}$

   $\chi^2 = \frac{25}{10} + \frac{1}{10} + \frac{1}{10} + \frac{9}{10} + \frac{4}{10} + \frac{0}{10}$

   $\chi^2 = 2.5 + 0.1 + 0.1 + 0.9 + 0.4 + 0$

   $\chi^2 = 4.0$

2. 유의성 판단:
   
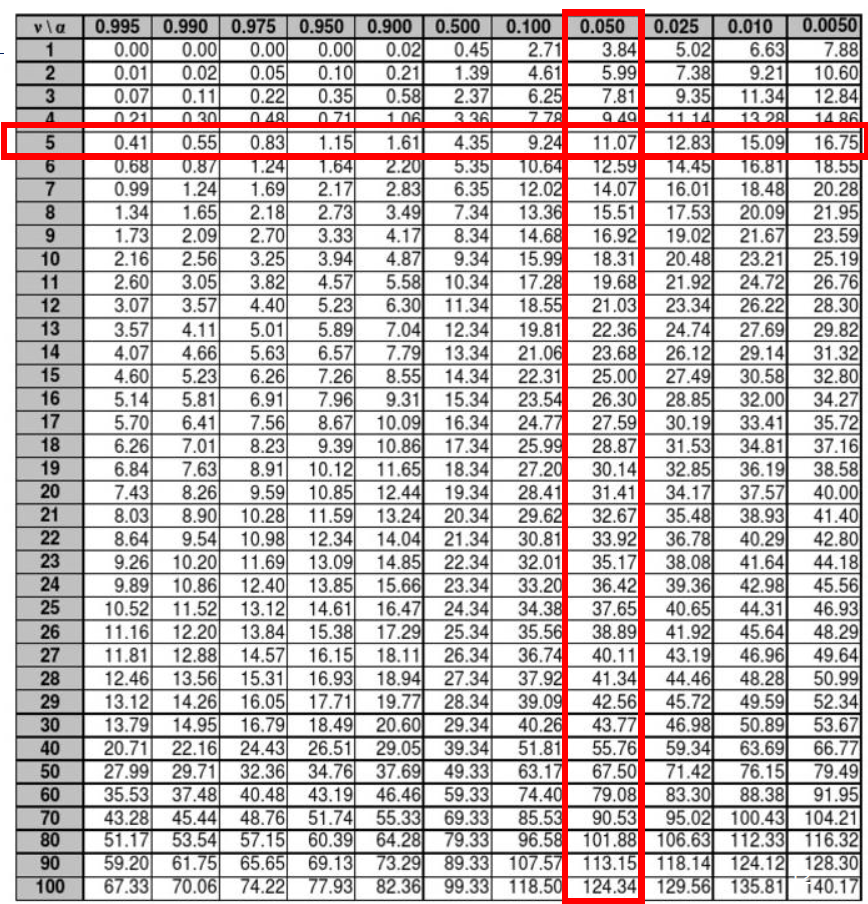
   자유도 5로 카이제곱 분포와 비교한다. $\chi^2 = 4.0$이고 유의 수준 5%에서 임계값이 11.07이면 귀무가설($H_0$)을 기각하지 못하므로, 주사위는 공정한 것으로 볼 수 있다.

Eg2.

판촉 행사 동안 한 가게는 세 가지 종류의 기념품(펜, 노트북, 열쇠고리)을 제공한다. 고객의 관심에 따라 40%가 펜을 선택하고, 40%가 노트북을 선택하며, 20%가 열쇠고리를 선택할 것으로 예상된다. 200명의 고객 중 70명이 펜을 선택하고, 100명이 노트북을 선택하며, 30명이 열쇠고리를 선택했다.(한쪽의 5% 유의 수준을 고려)
해석: 사람들의 선호도가 예측한 정도인 4:4:2정도인지 테스트를 하는 것이다.

Answer

1. 기대 빈도: 200명의 고객에 대해:

   • 펜: 0.4 x 200 = 80
   • 노트북: 0.4 x 200 = 80
   • 열쇠고리: 0.2 x 200 = 40

2. 카이제곱 통계량 계산:
   $\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}$

   여기서, $O_i$ = 관측 빈도, $E_i$ = 기대 빈도.

   $\chi^2 = \frac{(70 - 80)^2}{80} + \frac{(100 - 80)^2}{80} + \frac{(30 - 40)^2}{40}$

   $\chi^2 = \frac{100}{80} + \frac{400}{80} + \frac{100}{40}$

   $\chi^2 = 1.25 + 5 + 2.5$

   $\chi^2 = 8.75$

3. 해석:
   자유도 2에서 유의 수준 5%일 때 임계값은 5.99이다. 8.75 > 5.99이므로 귀무가설($H_0$)을 기각한다. 즉, 기념품의 분포가 예상과 유의미하게 다르다. 따라서 예측을 빗나갔다고 할 수 있다.

Eg3.

한 극장에서 드라마, 액션, 코미디 세 가지 장르의 영화를 상영하고 있다. 관객 분포가 균등할 것으로 예상된다. 하지만 150명의 관객 중 40명은 드라마를, 70명은 액션을, 40명은 코미디를 보았다.. 장르 선호도가 균등하게 분포되어 있는지 테스트하십시오.(한쪽의 5% 유의 수준을 고려)

Answer

예측된 선호도 : 50:50:50

$\chi^2 = \sum \frac{(O_i - E_i)^2}{E_i}$

여기서, $O_i$ = 관측 빈도, $E_i$ = 기대 빈도.

$\chi^2 = \frac{(40 - 50)^2}{50} + \frac{(70 - 50)^2}{50} + \frac{(40 - 50)^2}{50}=2+8+2=12$

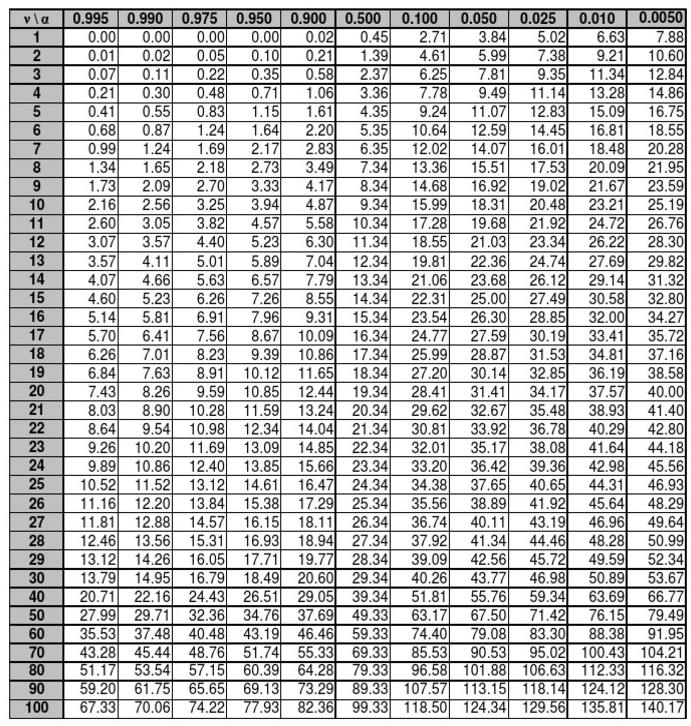
자유도 2에서 임계값은 5.99이다. 12 > 5.99이므로 귀무가설((H_0))을 기각한다. 선호도가 균등하지 않다.

4. F-test

Eg1.

두 클래스가 서로 다른 교육법을 사용하고 있으며, 시험 점수의 분산을 비교하여 한 방법이 더 일관된 점수를 유도하는지 확인하자. 클래스 A(12명 학생)의 분산은 20이고, 클래스 B(15명 학생)의 분산은 30이다. (5% 한측 유의 수준을 고려)
해석: 분산을 본다는 것은 절대적인 점수의 상승이 아니라 점수의 안정성을 보는 것이다.

Answer

1. 가설 설정:

   • 귀무 가설 (H0): 분산이 동일하다.
   • 대립 가설 (H1): 분산이 동일하지 않다.

2. F-통계량 계산:

   $F = \frac{s_1^2}{s_2^2}$

   여기서 $s_1^2$와$s_2^2$는 표본 분산이며 더 큰 분산을 분자로 사용하자.
   $F = \frac{30}{20} = 1.5$

3. 유의성 결정:
   자유도 $df_1 = n_1 - 1$ 및 $df_2 = n_2 - 1$을 가진 F-분포와 비교한다. 여기서 $n_1 = 15$이고 $n_2 = 12$이다. F-표에서 $F_{(14, 11)}$를 확인한다. 여기서 $df1$과 $df2$의 순서를 헷갈리지 않도록 주의하자.
   관찰된 F 값이 임계 값보다 크면 귀무 가설을 기각하고, 그렇지 않으면 분산이 유의미하게 다르지 않다고 결론을 내린다.
   
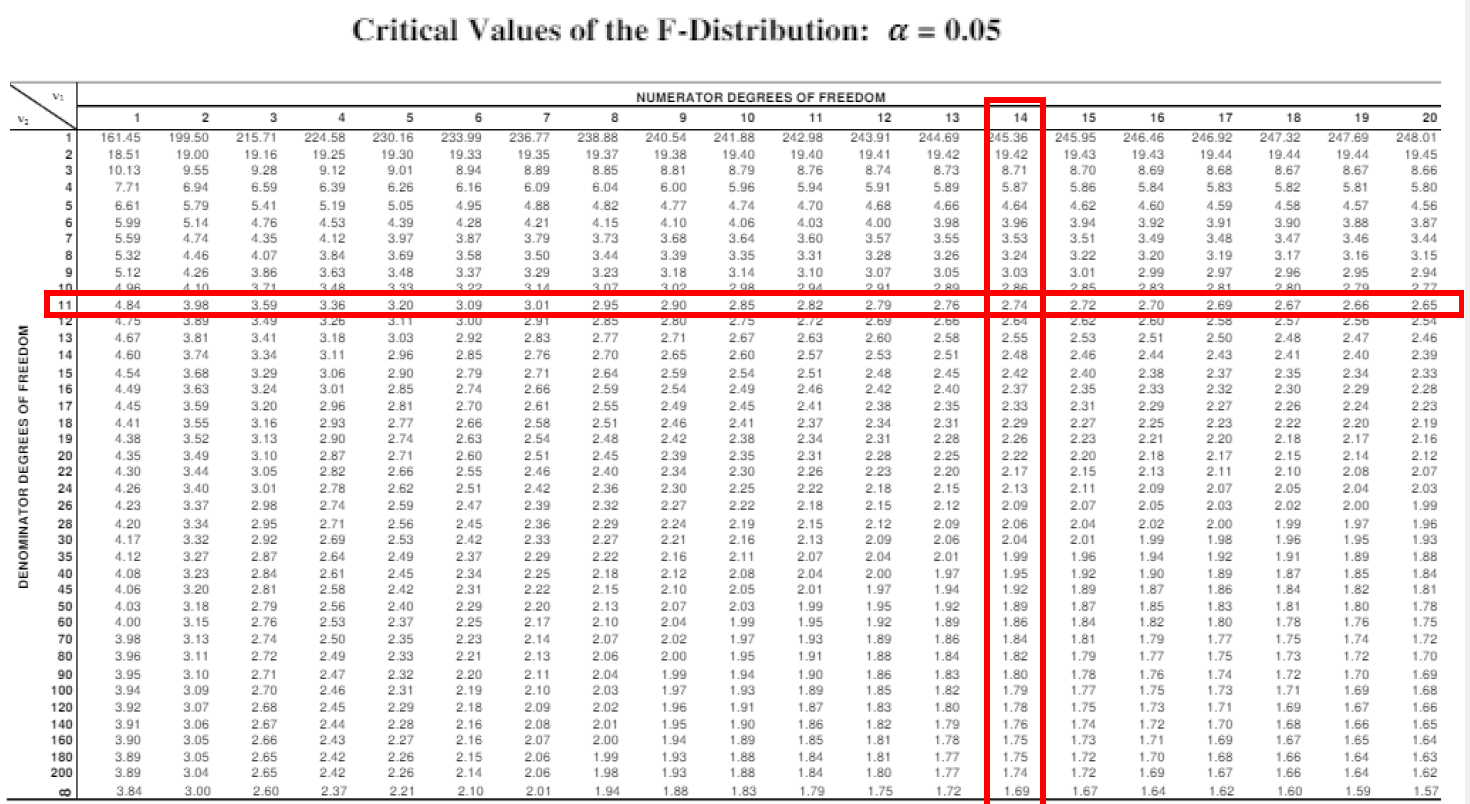
   $\alpha$값에 따라 테이블이 다른다.(테이블이 여러개 주어질 수도 있다)
   F 값(1.5)이 임계 값(2.74)보다 작으므로, 귀무 가설을 기각하지 않는다. 분산에 유의한 차이가 없다.
   해석하면, 두 교육법상에 큰 차이가 없다.

Eg2.

두 개의 다른 화학 용액 배치가 점도의 일관성을 위해 분석되었다. 배치 A (15 샘플)는 분산이 50이고, 배치 B (12 샘플)는 분산이 30이다.
(5% 유의 수준(단측검정)을 고려)

Answer

1. 가설 설정:

   • 귀무 가설 (H0): 분산이 동일하다.
   • 대립 가설 (H1): 분산이 동일하지 않다.

2. F-통계량 계산:
   $F = \frac{s1^2}{s2^2}$
   여기서 $s1^2$와 $s2^2$는 표본 분산이다. 더 큰 분산을 분자로 사용한다.
   $F = \frac{50}{30}=1.67$

3. 유의성 결정:

자유도 $df1 = 14$와 $df2 = 11$에서 5% 유의 수준의 임계 F-값은 2.74이다. $1.76 < 2.74$이므로, 귀무 가설을 기각하지 않는다. 분산에는 유의한 차이가 없다.

Eg3.

실험에서 한 기계는 분산이 22인 부품을 생산하고 (샘플 수 11), 다른 기계는 분산이 14인 부품을 생산한다 (샘플 수 9). 분산에 유의한 차이가 있는지 검정하자. (5% 한측 유의 수준을 고려)

Answer

1. 가설 설정:

   • 귀무 가설 (H0): 분산이 동일하다.
   • 대립 가설 (H1): 분산이 동일하지 않다.

2. F-통계량 계산:
   $F = \frac{s1^2}{s2^2}$
   여기서 $s1^2$와 $s2^2$는 표본 분산이다. 더 큰 분산을 분자로 사용한다.
   $F = \frac{22}{14} = 1.57$

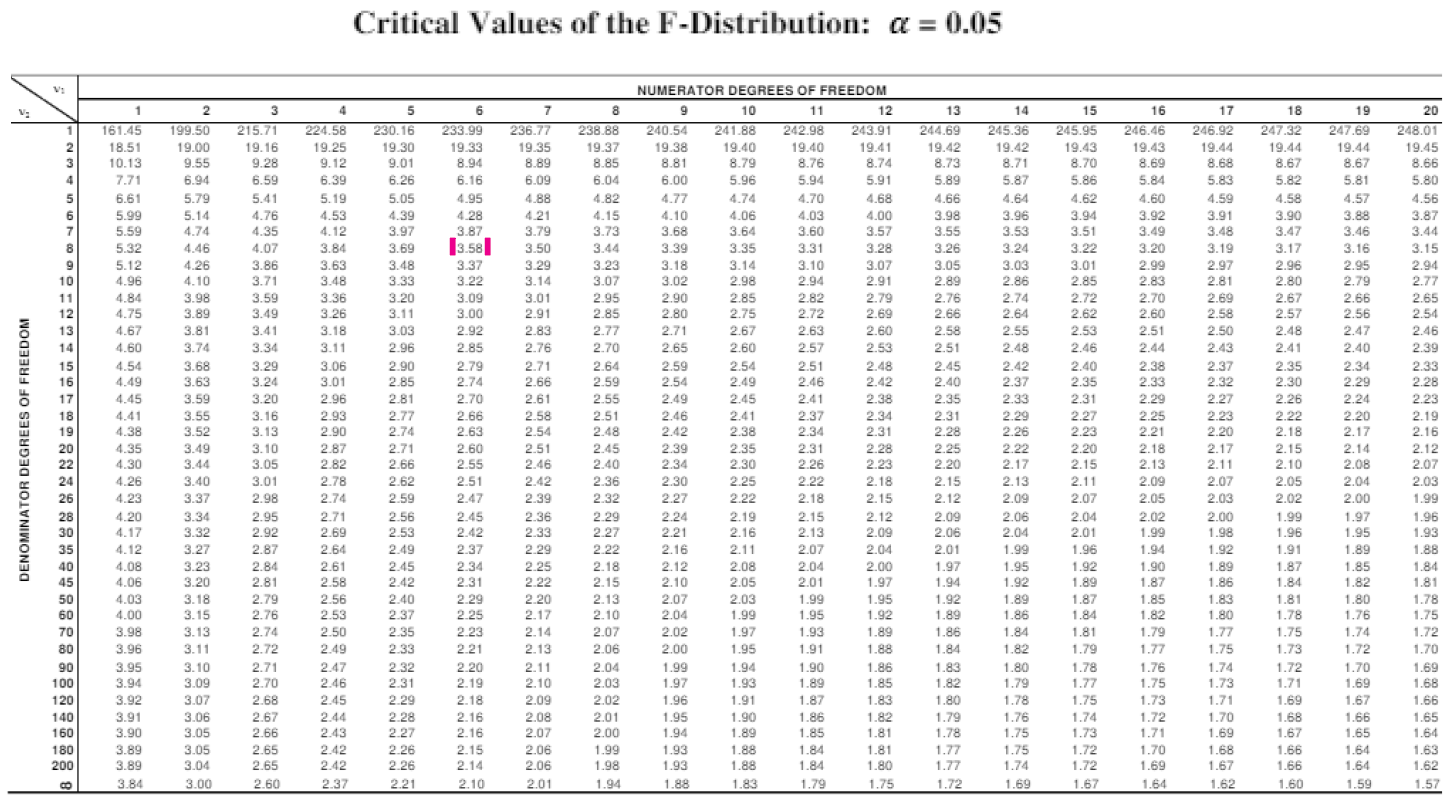
자유도 $df_1 = 10$ 및 $df_2 = 8$을 가진 F-분포와 비교한다. 임계 F-값은 약 3.58이다.
F 값(1.57텍스트)이 임계 값(3.58)보다 작으므로, 귀무 가설을 기각하지 않는다. 분산은 유의하게 다르지 않다.

정리

Z-검정 (Z-test)에서 Z-값이 임계 값(α)을 초과할 때 귀무 가설을 기각한다.
T-검정 (T-test)에서 T-값이 임계 값(α)을 초과할 때 귀무 가설을 기각한다.
카이제곱 검정 (Chi-Square test)에서 계산된 카이제곱 값이 임계 값(α)을 초과할 때 귀무 가설을 기각한다.
F-검정 (F-test)에서 계산된 F-값이 임계 값을 초과할 때 귀무 가설을 기각한다.