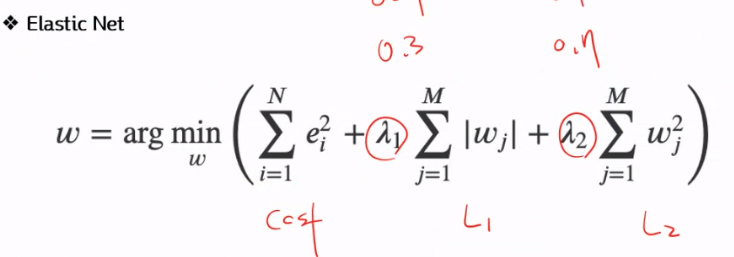머신러닝 성능을 향상시키는법

나에게 데이터셋 10만개가 있다면?

학습했던 데이터로 다시 검증한다.
→ 검증결과를 신뢰할 수 없다.(ex. 스카이캐슬, 예서 - 시험문제로 학습)

새로운 데이터를 수집해서 검증한다.
→ 너무 수고롭거나 불가능하다.

기존의 10만개 데이터셋 중에 일부는 학습데이터로 사용하지 않는다.
검증할 데이터로 따로 남겨두는 것이다.
학습데이터와 테스트데이터의 비율은 상황에 따라, 9:1 ~ 5:5

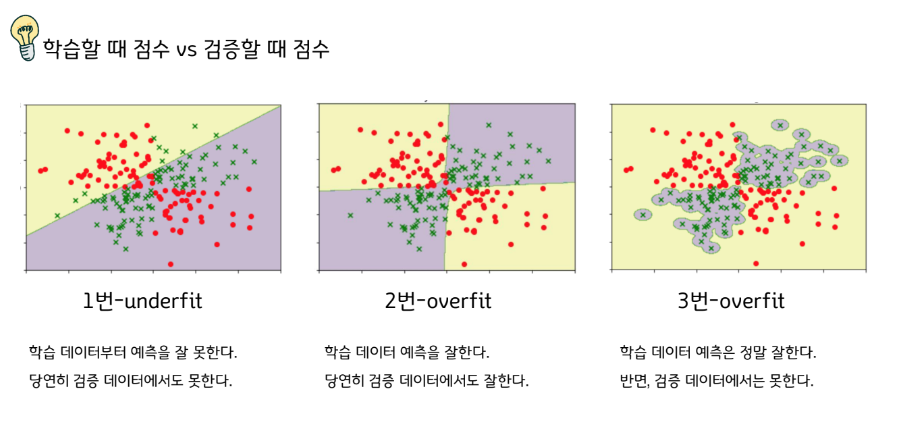
학습했던 문제는 잘 맞추지만,
학습할 때 본 적이 없는 새로운 문제는 잘 못푼다면,
그 학습은 별 의미가 없는 꼴이 된다.

학습할 땐 잘하는데 시험을 못본다면

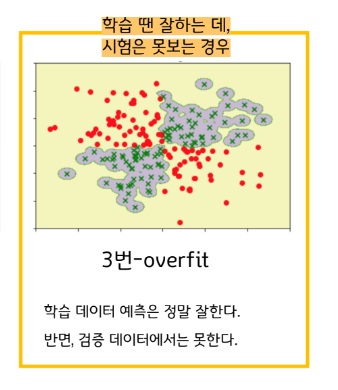
학습을 잘한다는 의미는

1 학습문제도 잘 맞춰야겠지만 (오차 최소화)
2 학습문제의 전체적인 경향도 잘 파악해서, 같은 경향의 새로운 문제가 나와도 잘 맞추는 것이다. (일반화)

학습문제의 전체적인 경향도 잘 파악한다는 말은 바꿔 말하면,
문제의 복잡도에 적합하게 학습해야 한다는 말이다.
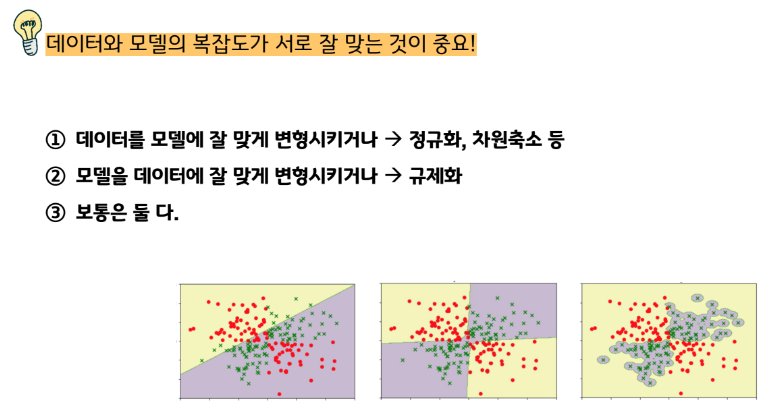
아래 그림을 문제의 복잡도와 경계선의 복잡도를 비교하면서 다시 살펴보자.

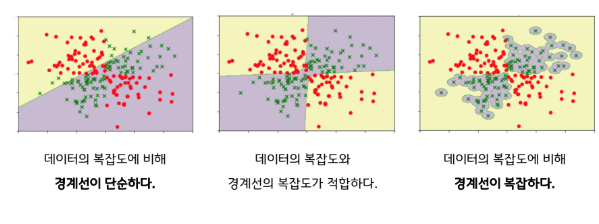
어떻게 모델의 복잡도에 제한을 걸어줄 수 있을까?

우선, 복잡도를 수치화 할 수 있어야 하지 않을까? 기계에게 명령을 내려야 하니 말이다.
복잡도를 대표하는 수치는 모델의 Weight의 총 크기다.
하나의 모델에는 보통 여러 Weight로 구성되어 있는데, 이 모든 Weight의 총 크기가 모델의 복잡도를
대표한다.

데이터에 모델의 복잡도를 맞추는 관점에서만 설명했지만,
사실 데이터도 변경 불가능한 것이 아니기 때문에 그 반대의 관점도 살펴볼 필요가 있다.

지도학습

Linear Regression

데이터를 보고, 학습의 목적을 생각하여 적절한 “hypothesis의 폼”을 결정하는 것은 사람의 몫이라 했다.
여기서 사람이 결정해야 한다는 “hypothesis의 폼”이 바로 앞으로 배워나갈 다양한 “머신러닝 모델”이다.
쉽게 말해서, 다양한 머신러닝 모델들 가운데 지금 데이터셋과 학습 목적에 맞는 hypothesis의 폼은 어떤 모델인지를 판단하는 것이 사람의 몫이기에 앞으로 최대한 다양한 머신러닝 모델들을 배워나가야 한다는 뜻이다.

그럼 Linear Regression은 어떻게 Hypothesis를 설정하는걸까?
1) 선형적으로 (→ ‘(비교적) 단순하게’ 정도로 이해하자)
2) 회귀분석용으로 (→ x와 실제숫자 y의 관계식 찾기 ) * 지도학습인건 말 안해도 다 아시죠?
➔ 종합하자면, Linear Regression이란 “(비교적) 단순한 X와 실제숫자 Y의 관계식” 정도가 된다.

그럼 Linear Regression은 어떻게 Cost를 계산하는지 알아보자.
앞서 머신러닝 개론에서 다룬 예시가 Linear Regression 이었다는 것을 이제 알 것이다.
여기서 Cost 계산은 어떻게 했는가. 모든 실제값과 예측값의 차이를 종합하여 계산했다.

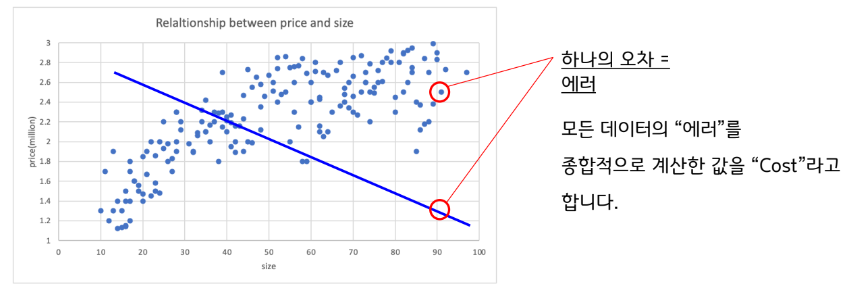
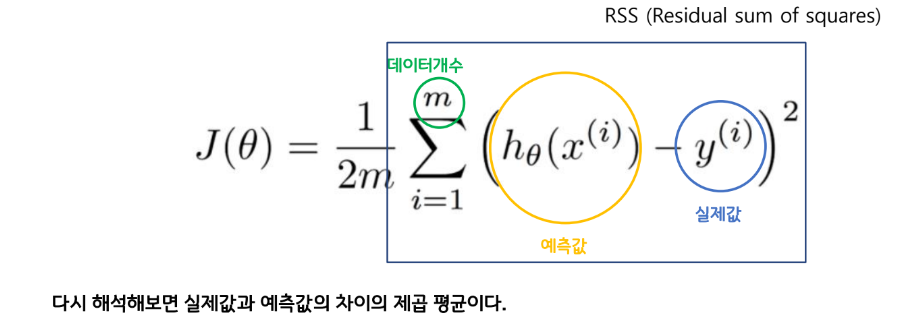
좀 더 자세히 말하자면, 모든 데이터셋에 대하여 오차를 제곱한 값을 평균낸 값을 Cost로 계산한다.
오차를 제곱하는 이유는 부호가 서로 다른 오차값들의 평균을 계산할 때 상쇄되는 것을 방지하기 위함이다.
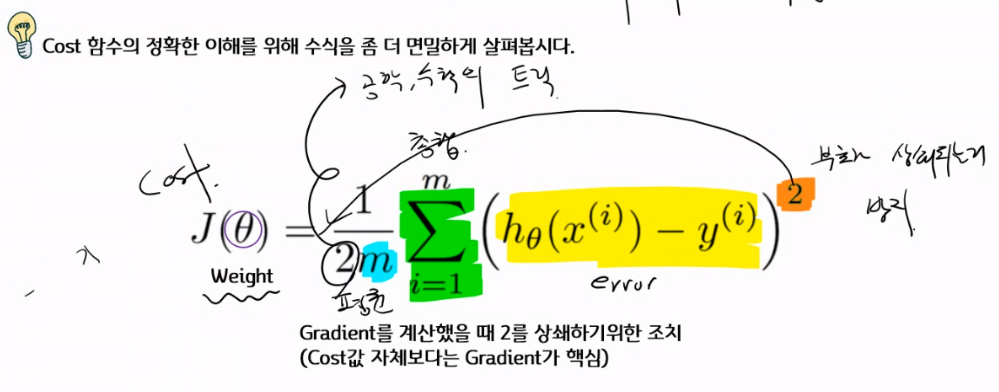
이를 수식으로 나타내보면 아래와 같다. (수식울렁증이 있는 이들은 다시한번 심호흡을 하고 하나씩 살펴보자)

argmin 특강 (사실상 머신러닝의 핵심?!)

수학에는 “A가 최소가 되게 만드는 B를 찾는다”는 의미를 가직 수식이 있다.

이를 Argument Min, Argmin 이라고 부르고 수식으로는 아래와 같이 쓴다.

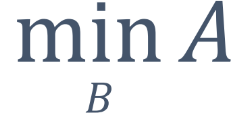
그럼 Hypothesis의 폼을 Linear Regression으로 정하고,
Cost가 작아지도록 Weight값을 학습시켜 나가는 과정을 수식으로 표현해보면 아래와 같다.

Linear Regression의 규제화

Regularization??
이토록 단순해보이는 Linear Regression에 또 Regularization을 한다니, 불필요해보인다.
하지만, 사실 상 그렇지 않은 경우가 많다.
다음을 알고 있다면 어렵지 않게 이해할 수 있다.
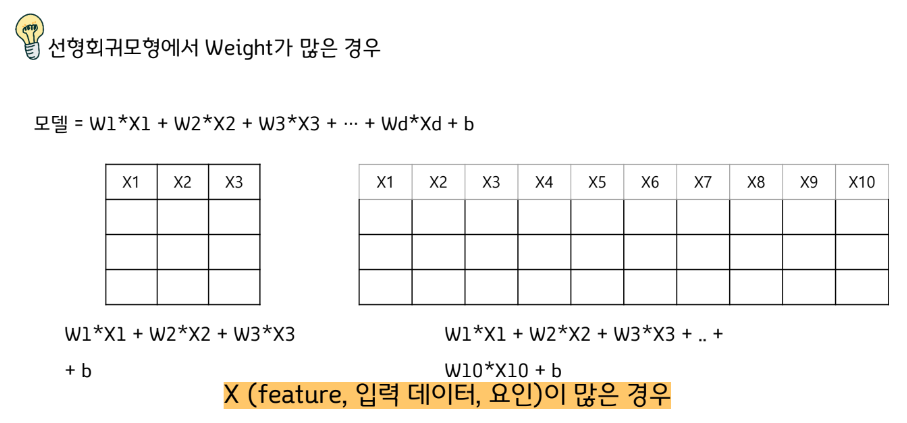
방정식보다 미지수가 많은 경우, 해는 무수히 많다.
데이터보다 (찾아야 하는) Weight가 많은 경우, 해는 무수히 많다.
(=Overfitting이 일어날 수 있다.)

선형회귀모형에서 규제의 종류

Elastic Net의 Cost

Elastic Net은 Ridge와 Lasso를 모두 고려한 규제라고 생각하면 된다.
Lasso항의 파라미터 l1_ratio x alpha 라면 Ridge항의 파라미터는(1- l1_ratio) x 1/2alpha이다.