가장 긴 증가하는 부분 순열 ( LIS )

LIS ( Longest Increasing Subsequence ) 가장 긴 증가하는 부분 순열.

주어진 수열 내에서 가장 긴 증가하는 부분 수열을 찾아내는 알고리즘.

아래와 같은 수열에서 LIS는 [10,20,50,90] 혹은 [10,20,40,60]이다.

1. dp를 이용한 구현.
가장 간단한 구현이며, 직관적이다. 하지만 $O(N^2)$의 시간 복잡도를 가지고 있어 적당히 큰 N에 대해서는 TLE를 낼 수 있다.

for i in range(N):
    if dp[i] == 0:
        dp[i] = 1
    for j in range(i):
        if arr[i] > arr[j]:
            dp[i] = max(dp[i],dp[j]+1)

2. dp + Binary Search를 이용한 구현
LIS를 구하는데 최적의 시간 복잡도를 가지고 있는 알고리즘이다. $O(NlogN)$의 시간 복잡도를 가진다.

과정은 다음과 같다.

- 배열의 각 요소를 순회하면서 LIS 배열이 오름차순을 유지하도록 삽입
- 이 때 binary search를 사용.

1. LIS 배열의 최댓값(마지막 값)보다 배열의 요소가 크다면, 마지막에 추가
   

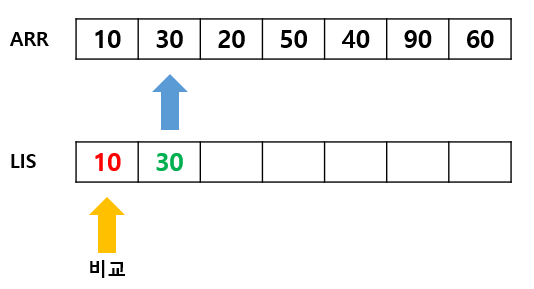
2. LIS의 배열의 최댓값(마지막 값)보다 배열의 요소가 작다면, binary search를 통해 LIS 배열에 배열의 요소가 들어갈 위치를 찾을 수 있음. ( LIS는 오름차순으로 정렬되어 있기 때문. ) 위치를 찾으면 원래 LIS 배열에 있던 값과 교환.
   

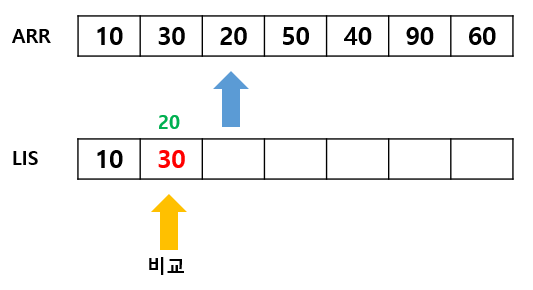
3. 위 과정을 반복하여 LIS를 채우고, arr 배열을 전부 순회했을 때 LIS의 길이가 LIS의 길이이다.

from bisect import bisect_left

N = 100000

def LIS(n):
    maxVal = 0

    for i in range(n):
        if i == 0 or lis[-1] < arr[i]:
            lis.append(arr[i])
            trace[i] = len(lis)-1
            maxVal = trace[i]
        else:
            pos = bisect_left(lis, arr[i])
            lis[pos] = arr[i]
            trace[i] = pos
    print(maxVal+1)

    res = []
    for i in range(n-1,-1,-1):
        if trace[i] == maxVal:
            res.append(arr[i])
            maxVal -= 1
    res.reverse()
    print(*res)