손실함수-(Loss Function, Cost Function)

손실 함수

딥러닝 모델의 학습 지표

• Accuracy
  • 모델이 얼마나 잘 맞췄는가에 초점을 두는 것
  • 사람이 모델을 평가하는 기준을 보통 정확도를 사용
• Loss
  • 모델이 얼마나 잘 못 맞췄는가에 초점을 두는 것
  • 모델이 자기 자신을 평가하는 기준이 된다.

지표란?

• 기준
• 식사를 해야하는데 배가 부른 것을 기준으로 할지, 배가 고픈 것을 기준으로 할지
• 잘 맞춘 것을 기준으로 : Accuracy
• 맞추지 못한 것을 기준으로 : Loss

평균 제곱 오차( Mean Squared Error )

• $y_k$ : 신경망의 예측값
• $t_k$ : 정답 레이블
• $k$ : 데이터의 차원 수
  • 차원 수 : 클래스의 개수

    강아지, 고양이, 말을 예측하는 문제면 $k$가 3
    MNIST 손글씨 데이터 셋이면 $k$가 10

• 보통 신경망에서는 MSE를 사용하지 않고 Cross Entropy Error를 활용
• Cross Entropy Error가 MSE보다 훨씬 효율적이기 때문
• MSE를 배우는 이유는

  1. 회귀 문제를 풀기에 적합
  2. 단순하게 loss에 대한 공부가 쉽기 때문에

• 정상적인 $\frac{1}{n}$을 사용하지 않고 $\frac{1}{2}$을 사용한 이유는 MSE를 미분 했을 때 남는 것은 순수한 오차라고 할 수 있는 $y-t$ 만 남기 때문에

import numpy as np

y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]) # 2번 클래스로의 예측 확률이 60%
t = np.array([0,      0,   1,   0,    0,   0,   0,   0,   0,   0]) # 정답은 2라는 이야기 이다. 클래스의 개수만큼 One Hot Encoding이 되어있는 상태

# 각 클래스 별 순수한 오차
y - t

~~> 
array([ 0.1 ,  0.05, -0.4 ,  0.  ,  0.05,  0.1 ,  0.  ,  0.1 ,  0.  ,0.  ])

MSE 구현하기

def mean_squared_error(y, t):
    return 0.5 * np.sum((y-t)**2)

print('정답을 2로 추정했을 때의 MSE 값( 0.6 ) : {:3.f}' .format(mean_squared_error(y, t)))

~~> 정답을 2로 추정했을 때의 MSE 값( 0.6 ) : 0.098

y = np.array([[0.0, 0.05, 0.8, 0.0, 0.05, 0.0, 0.0, 0.1, 0.0, 0.0])	# 2번 클래스로의 예측 확률이 80%
print('정답을 2로 추정했을 때의 MSE값( 0.8 ) : {:.3f}' .format(mean_squared_error(y, t)))

~~> 정답을 2로 추정했을 때의 MSE값( 0.8 ) : 0.027

y = np.array([0.0, 0.8, 0.05 , 0.0, 0.05, 0.0, 0.0, 0.1, 0.0, 0.0]) # 2번 클래스로의 예측 확률이 5%, 1번 클래스로의 예측은 80%
print("정답을 1로 추정했을 때의 MSE값( 2로 추정한 확률 : 0.05 ) : {:.3f}".format(mean_squared_error(y, t)))

~~> 정답을 1로 추정했을 때의 MSE값( 2로 추정한 확률 : 0.05 ) : 0.777

y = np.array([0.0, 0.05, 0.8, 0.0, 0.05, 0.0, 0.0, 0.1, 0.0, 0.0]) # 2번 클래스로의 예측 확률이 80%
t = np.array([0,      0,   1,   0,    0,   0,   0,   0,   0,   0]) # 정답은 2라는 이야기 이다. 클래스의 개수만큼 One Hot Encoding이 되어있는 상태
print('정답을 2로 추정했을 때의 MSE 값( 0.8 ) : {:.3f}' .format(mean_squared_error(y, t)))

~~> 정답을 2로 추정했을 때의 MSE 값( 0.8 ) : 0.027

y = np.array([0.0, 0.8, 0.05, 0.0, 0.05, 0.0, 0.0, 0.1, 0.0, 0.0]) # 2번 클래스로의 예측 확률이 5%, 1번 클래스로의 예측은 80%
t = np.array([0,      0,   1,   0,    0,   0,   0,   0,   0,   0]) # 정답은 2라는 이야기 이다. 클래스의 개수만큼 One Hot Encoding이 되어있는 상태
print('정답을 2로 추정했을 때의 MSE 값( 0.05 ) : {:.3f}' .format(mean_squared_error(y, t)))

~~> 정답을 2로 추정했을 때의 MSE 값( 0.05 ) : 0.777

교차 엔트로피 오차(Cross Entropy Error)

• $t_k$는 OHE( One Hot Encoding )이 되어있는 상태
• $k$는 데이터의 차원
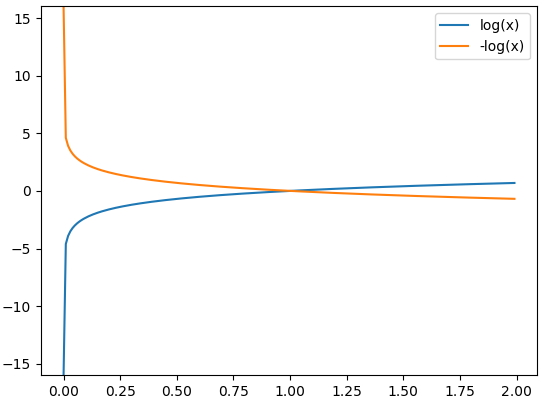
• 예측 확률이 낮으면 낮을 수록 Loss 값은 커진다.
• 정답 레이블의 소프트맥스의 결과가 $0.6$ 이라면 -$log0.6$을 구한 것과 똑같다.

Cross Entropy Error 구현하기

def cross_entropy_error(y, t):
	delta = 1e-7 
    # ㄴ delta : 아주 작은 값, log 0은 음수 무한대가 되기 때문에 아주 작은 값은 delta를 임의로 더해준다.
    return -np.sum(t*np.log(y+delta))

💡 np.log 함수에 0이 대입되면 ( 즉 예측값 $y_k$, 가 0 이면 ) 음수 무한대가 되어 버린다. 따라서 아주 작은 값인 delta를 더해준다.

t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0]) # 정답은 2라는 이야기 이다. 클래스의 개수만큼 One Hot Encoding이 되어있는 상태

y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]) # 2번 클래스로의 예측 확률이 60%
print("정답을 2로 추정했을 때의 CEE값(0.6) : {:.3f}".format(cross_entropy_error(y, t)))

y = np.array([0.1, 0.05, 0.8, 0.0, 0.05, 0.0, 0.0, 0.0, 0.0, 0.0]) # 2번 클래스로의 예측 확률이 80%
print("정답을 2로 추정했을 때의 CEE값(0.8) : {:.3f}".format(cross_entropy_error(y, t)))

y = np.array([0.7, 0.05, 0.1 , 0.0, 0.05, 0.0, 0.0, 0.1, 0.0, 0.0]) # 2번 클래스로의 예측 확률이 10%, 0번 클래스로 예측한 확률이 70%
print("정답을 0로 추정했을 때의 CEE값( 2로 추정한 확률은 0.1 ) : {:.3f}".format(cross_entropy_error(y, t)))

~~>
정답을 2로 추정했을 때의 CEE값(0.6) : 0.511
정답을 2로 추정했을 때의 CEE값(0.8) : 0.223
정답을 0로 추정했을 때의 CEE값( 2로 추정한 확률은 0.1 ) : 2.303

Cross Entropy Error의 해석

• 정답 레이블의 확률만을 계산 하는 것
• 정답 예측 확률이 낮아지면 Loss가 매우 크게 증가 👉 고쳐야 될 것이 많다.
• 정답 예측 확률이 높아지면 Loss가 완만하게 감소 👉 고쳐야 할 것이 많이 없어진다.