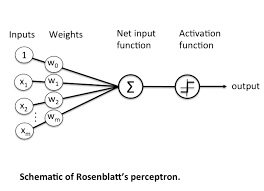
퍼셉트론(Perceptron)

김선재·2021년 10월 6일

Deep Learning

목록 보기

1/13

퍼셉트론

인공 뉴런이라고도 한다.
뇌과학에서는 신경으로 들어오는 일정한 자극, 신경망에서는 feature(특성)가 된다.
입련된 신호(특성)는 어떠한 흐름을 타면서 처리가 된다.
처리가 완료되면 거기에 대한 결과가 퍼셉트론의 출력이 된다. $y = \begin{cases} 0 \enspace (w_1x_1 + w_2x_2 \leq \theta) \\ 1 \enspace (w_1x_1 + w_2x_2 > \theta) \end{cases}$ $w_1x_1+w_2x_2$ 의 결괏값이 임의의 임계점 ( $\theta$ )를 넘지 못하면 0, 넘으면 1이 된다.
이러한 수식을 반응 조건 계산식 이라고 한다.

# 조건문을 써야 할까?
# 퍼셉트론의 w와 theta는 지금으로썬 알 수가 없다.
# 따라서 임의로 설정하기로 한다.

def perceptron1(x1, x2):
	# 임의의 가중치인 w1, w2를 설정
    w1, w2 = 0.5, 0.5
    
    # 임의의 임계값인 theta를 설정
    theta = 2.0
    
    # 출력값 y 구하기
    y = (w1 * x1) + (w2 * x2)
    
    return y, y >= theta
    
# 시각화
# 입력 데이터 생성
x1 = np.linspace(-3, 7, 100)
x2 = np.linspace(-3, 7, 100)

# 퍼세브론의 결과물 구하기
y_value, y_result = perceptron1(x1, x2)

~~> (array([-3.        , -2.8989899 , -2.7979798 , -2.6969697 , -2.5959596 ,
        -2.49494949, -2.39393939, -2.29292929, -2.19191919, -2.09090909,
        -1.98989899, -1.88888889, -1.78787879, -1.68686869, -1.58585859,
        -1.48484848, -1.38383838, -1.28282828, -1.18181818, -1.08080808,
        -0.97979798, -0.87878788, -0.77777778, -0.67676768, -0.57575758,
        -0.47474747, -0.37373737, -0.27272727, -0.17171717, -0.07070707,
         0.03030303,  0.13131313,  0.23232323,  0.33333333,  0.43434343,
         0.53535354,  0.63636364,  0.73737374,  0.83838384,  0.93939394,
         1.04040404,  1.14141414,  1.24242424,  1.34343434,  1.44444444,
         1.54545455,  1.64646465,  1.74747475,  1.84848485,  1.94949495,
         2.05050505,  2.15151515,  2.25252525,  2.35353535,  2.45454545,
         2.55555556,  2.65656566,  2.75757576,  2.85858586,  2.95959596,
         3.06060606,  3.16161616,  3.26262626,  3.36363636,  3.46464646,
         3.56565657,  3.66666667,  3.76767677,  3.86868687,  3.96969697,
         4.07070707,  4.17171717,  4.27272727,  4.37373737,  4.47474747,
         4.57575758,  4.67676768,  4.77777778,  4.87878788,  4.97979798,
         5.08080808,  5.18181818,  5.28282828,  5.38383838,  5.48484848,
         5.58585859,  5.68686869,  5.78787879,  5.88888889,  5.98989899,
         6.09090909,  6.19191919,  6.29292929,  6.39393939,  6.49494949,
         6.5959596 ,  6.6969697 ,  6.7979798 ,  6.8989899 ,  7.        ]),
 array([False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False, False, False,
        False, False, False, False, False, False, False, False, False,
        False, False, False, False, False,  True,  True,  True,  True,
         True,  True,  True,  True,  True,  True,  True,  True,  True,
         True,  True,  True,  True,  True,  True,  True,  True,  True,
         True,  True,  True,  True,  True,  True,  True,  True,  True,
         True,  True,  True,  True,  True,  True,  True,  True,  True,
         True,  True,  True,  True,  True,  True,  True,  True,  True,
         True]))

# 시각화
plt.plot(y_value, y_result)
plt.yticks([0, 1])
plt.xticks([-3, 2, 7], ['-∞', 'θ', '∞')])
plt.xlabel("w1x1+w2x2")
plt.ylabel("y", rotation=0)
plt.show()

~~>

$\theta$ 를 기준으로 $w_1x_1+w_2x_2$ 의 결과가 0 또는 1로 결정지어진다. 이걸 함수로 일반화 시켜서 어떤 상황에서든 수식을 사용할 수 있도록 일반화 시켜보기

원래 수식
$y = \begin{cases} 0 \enspace (w_1x_1 + w_2x_2 \leq \theta) \\ 1 \enspace (w_1x_1 + w_2x_2 > \theta) \end{cases}$
바뀐 수식
$y = \begin{cases} 0 \enspace (w_1x_1 + w_2x_2 -\theta \leq 0) \\ 1 \enspace (w_1x_1 + w_2x_2 -\theta > 0) \end{cases}$
일반화된 함수 지정하기
$z = w_1x_1 + w_2x_2 -\theta$
$y = \begin{cases} 0 \enspace (z \leq 0) \\ 1 \enspace (z > 0) \end{cases}$
$u(z) = \begin{cases} 0 \enspace (z \leq 0) \\ 1 \enspace (z > 0) \end{cases}$
함수 $u$ 는 단위 계단 함수
$y=u(z)$

z = np.linspace(-3, 3, 100)
plt.plot(z, z > 0)
plt.yticks([0, 1])
plt.xticks([-3, 0, 3], ['-∞', 'θ', '∞'])
plt.xlabel('z')
plt.ylabel('y=u(z)', rotation=0)
plt.show()

~~>

$\\y = \mathcal{u}(w_1x_1 + w_2x_2 - \theta)$
$z = w_1x_1 + w_2x_2 - \theta$
$y = u(z)$

계단 함수 $u$ 의 결과( $y$ )에 따라서 항상 0 또는 1만 가지게 된다.

단층 퍼셉트론, 다층 퍼셉트론

단층 퍼셉트론의 한계
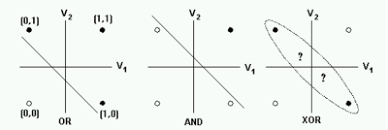
- 직선으로 나뉘는 두 영역을 만들기 때문에 선형분리만 가능
다층 퍼셉트론의 장점
- 단층 퍼셉트론의 한계를 극복하기 위해서 만들어졌다.
- 선형에서 비선형분리가 가능

AND 게이트

입력값 두개가 모두 1이어야만 결과물이 1이 된다.

def AND(x1, x2):
	# x1, x2에 대해서 조건 검사(if)를 하는 것은 퍼셉트론이 아니다.
    # w1x1 + w2x2 - theta의 결과물만 검사
    
    w1, w2, theta = 0.5, 0.5, 0.7
    z = w1*x1 + w2*x2 - theta
    
    return int(z > 0) # 부등호를 쓴 것이 계단 함수 u를 사용한 것
    
AND(0, 0), AND(1, 0), AND(0, 1), AND(1, 1)
~~> (0, 0, 0, 1)

편향(bias) 개념을 도입

수식에 음수가 있으면 표현하기 까다롭기 때문에 $\theta$ 를 $-b$ 로 표현
$\theta$ - $(-b)$

$y = \begin{cases} 0 \enspace (w_1x_1 + w_2x_2 + b \leq 0) \\ 1 \enspace (w_1x_1 + w_2x_2 + b > 0) \end{cases}$

퍼셉트론은 입력 신호에 가중치를 각각 곱합 값과 편향(bias)을 합하여 그 값이 0 이 넘으면 1 로, 0 을 넘지 않으면 0 으로 출력할 수 있도록 일반화

z = \sum_{i=1}^{n}(w_ix_i)+b

# 입력이 몇개가 될지 모르기 때문에 numpy로 표현
x = np.array([0, 1])
w = np.array([0.5, 0.5]) # 항상 w의 개수는 x의 개수와 일치해야 한다.
b = -0.7 # theta가 0.7 이었으니깐 bias는 -0.7

print("행렬 곱 : {} " .format(w*x))
print('각 원소의 곱을 합한 결과 : {} ' .format(np.sum(w*x)))
print('편향 추가 계산 : {:.1f} ' .format(np.sum(w*x)+b)) # wx + b

~~> 행렬 곱 : [0.  0.5] 
각 원소의 곱을 합한 결과 : 0.5 
편향 추가 계산 : -0.2

AND 게이트를 numpy로 구현

def AND(x1, x2):
	x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    
    z = np.sum(w*x) + b
    
    return int(z > 0)

AND(0, 0), AND(0, 1), AND(1, 0), AND(1, 1)
~~> (0, 0, 0, 1)

가중치와 편향에 대한 의미

가중치 : 입력값에 대한 중요도
- 각각의 입력값이 출력값에 얼마나 영향을 미치게 할 것인가?
  
  가중치가 크다 : 입력값이 출력값에 영향을 많이 미친다.
  가중치가 작다 : 입력값이 출력값에 영향을 많이 미치지 않는다.
편향 : 퍼셉트론이 얼마나 쉽게 활성화가 되는가를 결정해 준다.
- 활성화 : 퍼셉트론의 결과물이 1이 되면 활성화가 됐다고 한다
- 편향이 크면 퍼셉트론의 흥분도가 커져서 쉽게 활성화 된다. ( 민감한 퍼셉트론 )
- 편향이 작으면 퍼셉트론의 흥분도가 낮아져서 활성화가 잘 안된다.( 둔감한 퍼셉트론 )

NAND 게이트

AND 게이트의 부호를 반대로

def NAND(x1, x2):
	x = np.array([x1, x2])
    # 가중치와 편향의 부호를 AND 게이트의 반대로 설정
    w = np.array([-0.5, -0.5])
    b = 0.7
    
    z = np.sum(w * x) + b
    
    return int(z >0)
    
NAND(0, 0), NAND(0, 1), NAND(1, 0), NAND(1, 1)
~~> (1, 1, 1, 0)

OR 게이트

둘 중 하나라도 참 값이 있으면 참 값을 출력
AND 게이트의 편향을 적절하게 조절해 주면 된다.

def OR(x1, x2):
	x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    
    # 편향만 조절해 준다.
    b = -0.2 # 얼만큼 조절해야하는지는 모른다. -> 찾아야함
    
    z = np.sum(w * x) + b
    
    return int(z > 0)
    
OR(0, 0), OR(0, 1), OR(1, 0), OR(1, 1)
~~> (0, 1, 1, 1)

AND, NAND, OR는 각각 하나의 퍼셉트론으로써 각각의 연산을 충실히 수행
각각의 입력값을 받아서 각자의 역할을 수행하면, 한번에 입력에 대한 한번의 출력이 올바르게 이루어 진다. -> 단층 퍼셉트론

단층 퍼셉트론의 한계

XOR게이트 구현하기

OR 퍼셉트론에 대한 시각화

plt.figure(figsize=(4,4))

plt.scatter([0],[0], marker='o')
plt.scatter([1,0,1],[0,1,1], marker='^')
plt.xticks([0, 0.5, 1])
plt.yticks([0, 0.5, 1])
plt.xlim((-0.2,1.2))
plt.ylim((-0.2,1.2))
plt.xlabel('x_1')
plt.ylabel('x_2', rotation=0)

plt.show()
~~>

$z=w_1x_1 + b$

XOR 게이트 시각화

plt.figure(figsize=(4,4))

plt.scatter([0,1],[0,1], marker='o')
plt.scatter([1,0],[0,1], marker='^')
plt.xticks([0, 0.5, 1])
plt.yticks([0, 0.5, 1])
plt.xlim((-0.2,1.2))
plt.ylim((-0.2,1.2))
plt.xlabel('x_1')
plt.ylabel('x_2', rotation=0)

plt.show()
~~>

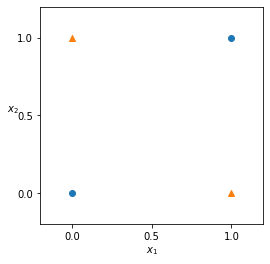
단층 퍼셉트론을 여러개 쌓아서 해결

단층 퍼셉트론을 여러 개 쌓아서 다층 퍼셉트론으로 만들어 주면 단층 퍼셉트론으로는 해결할 수 없던 일을 해결할 수 있다.

def XOR(x1, x2):
	s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    
    y = AND(s1, s2)
    
    return y

XOR(0, 0), XOR(0, 1), XOR(1, 0), XOR(1, 1)
~~> (0, 1, 1, 0)

김선재

data science!!, data analyst!! ///// hello world

다음 포스트