---

본 포스팅은 제가 읽었던 논문을 간단하게 정리하는 글입니다. 논문의 모든 내용을 작성하는 것이 아닌, 일부분만 담겨 있으므로 자세한 내용은 원본 논문을 확인해 주시기를 바랍니다. 또한, 논문을 잘못 이해한 부분이 있을 수 있으므로, 양해 바랍니다.

Overview

Weakly Supervised Object Detection(WSOD)에는 아래의 세 가지의 주요 문제가 있음.

1. Instance Ambiguity
   1. Missing Instances : Less salient object가 탐지되지 않음.
   2. Grouped Instances : Grouped object가 하나의 bounding box(bbox)로 탐지됨.
2. Part Domination : Object의 most discriminative parts만 탐지됨 → e.g., 사람 전체가 아닌 얼굴에만 bbox가 그려짐.
3. Memory Consumption : Selective Search, Edge Boxes 등과 같은 proposal generation method는 high recall을 위한 dense proposal을 생성하여 많은 메모리를 필요로 함.

이러한 문제 상황을 기반으로, 본 논문에서는 위의 세 문제를 해결하기 위한 self-training algorithm과 Concrete DropBlock, sequential batch back-propagation algorithm을 제안함.

The proposed method tackles Instance Ambiguity by introducing an advanced self training algorithm … The proposed method also addresses Part Domination by introducing a parametric spatial dropout termed ‘Concrete DropBlock’ … Finally, to alleviate the issue of Memory Consumption, our method adopts a sequential batch back-propagation algorithm …

Background

아래의 Figure 2를 통해 본 논문에서 제안하는 framework를 확인할 수 있음.

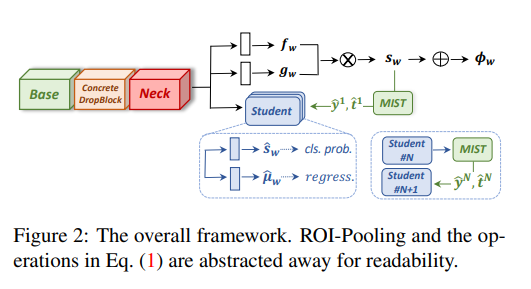
전체적으로 지금까지 소개했던 OICR, WSOD2 framework와 유사한 과정을 가짐.

Selective Search와 같은 proposal generation method를 통해 $R$개의 region proposal을 얻고, CNN backbone을 사용하여 해당 region에 대한 feature를 얻음.

Feature는 이후 fc layer를 통과하여, 모든 object category $c$와 모든 region $r$에 대한 classification logits $f_w(c,r) \in \mathbb R$과 detection logits $g_w(c,r) \in \mathbb R$로 계산됨.

Score matrix는 아래와 같이 softmax 함수로 계산되며, final score $s_w(c,r)$은 두 score matrix의 element-wise product로 계산됨.

Image evidence $\phi_w(c)$는 모든 region의 합으로 계산되며, Ground truth(GT) image label과 함께 loss function에 사용됨.

$y(c) \in \{0,1\}$이며 1일 경우 category $c$가 해당 이미지 내 존재하는 것을 의미함.

Online self-training을 사용하기 위해, region score $s_w(c,r)$을 기반으로 pseudo label $\hat y(c,r)$을 생성하여 student layer(이전의 refinement layer)를 학습시킴. $\hat s_w(c|r)$은 student layer의 output을 의미함.

Approach

지금까지의 background는 이미 제안된 아키텍처의 구조를 간단히 설명한 것임. 이번 섹션에서는 본 논문에서 제안하는 알고리즘에 대해 주로 알아봄.

Multiple instance self-training (MIST)

MIST framework를 설계할 때 Instance-associative, Representativeness, Spatial-diversity를 고려하여 알고리즘을 설계하였음.

MIST 알고리즘은 아래의 순서를 따름.

1. 이미지 내 존재하는 클래스 $c$ 기준, score $s(c,r)$을 기준으로 집합 $R$을 정렬함. $R$은 모든 proposal $r$을 포함하는 집합임.
2. 정렬된 $R$에서, 상위 $p$ 퍼센트의 region을 선택하여 initial candidate pool $R'(c)$를 생성함. Candidate pool의 크기 $|R'(c)|$는 image-adaptive 하여, 생성되는 region의 수 $|R|$에 따라 달라짐.
3. Diverse set of high-scoring non-overlapping regions을 얻기 위해, $R'(c)$에 non-maximum suppression(NMS)을 적용함. NMS 출력 결과를 pseudo boxes $\hat R(c)$로 사용함.

Self-training with regression

보다 정확한 bbox를 얻기 위해, Student block에 classification layer뿐만 아니라 bbox regression layer를 추가함.

Regression layer에서 예측된 bbox를 $\mu_w(r)$이라 하면, $\mu_w(r)$과 pseudo label $\hat R$을 사용하여 bbox regression을 진행함.

모든 region $r$에 대해, 만약 $r$이 pseudo-box $\hat r \in \hat R$과 많이 겹쳐있다면 $\hat r$을 사용하여 $r$에 대한 regression target $\hat t(r)$과 classification label $\hat y(c,r)$를 생성함. $\hat t(r)$는 $\hat r$의 좌표를 기반으로 생성되고, $\hat r$의 클래스가 $c$일 때 $\hat y(c,r)=1$로 설정됨.

Student block의 region-level loss는 아래와 같음.

$\lambda_r$은 OICR 논문에서 제안된 per-region weight $w_r^k$를 의미함.

Self-ensembling

성능을 향상하기 위해 여러 개의 student block을 사용함. 첫 번째 pseudo-label은 teacher branch로부터 생성되며, student block $N$은 $N+1$번째 student block을 위한 pseudo-label을 생성함.

Concrete DropBlock

존재하는 WSOD 아키텍처의 문제점 중 하나는 객체의 전체 부분이 아닌 가장 discriminative 한 부분만을 탐지하는 것임. 이러한 문제를 해결하는 가장 자연스러운 방법은 most discriminative part를 dropping 하는 것임.

공간에 대한 dropout(spatial dropout)을 수행하는 연산으로 DropBlock이 있음. DropBlock은 아래 그림 Figure 2처럼 특정한 sample mask를 선택한 후, mask 인근의 모든 영역을 drop 함. 추가적인 내용은 이 블로그를 참고.

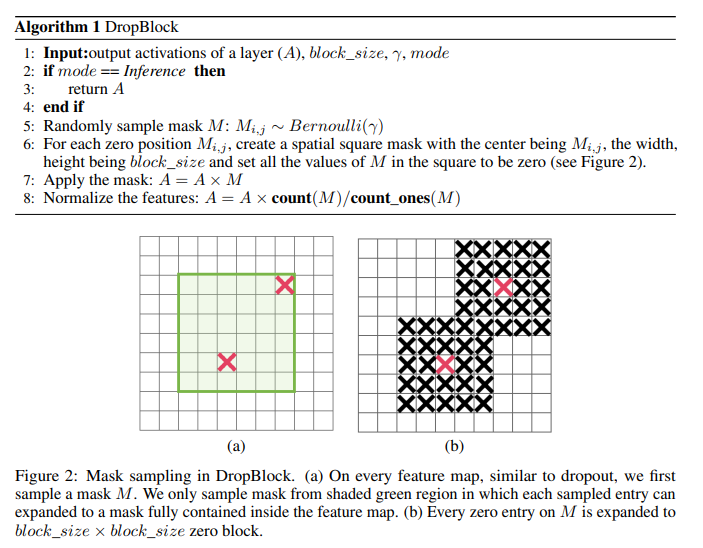
DropBlock의 경우 non-parametric regularization technique로, 기본적으로 모든 region을 동일하게 취급함.

Most discriminative point를 보다 잘 drop 할 수 있도록, 본 논문에서는 Concrete DropBlock을 제안함. Concrete DropBlock는 data-driven, parametric 하며 end-to-end로 학습 가능함.

아래 Figure 3는 Concrete DropBlock의 전체적인 과정을 표현함.

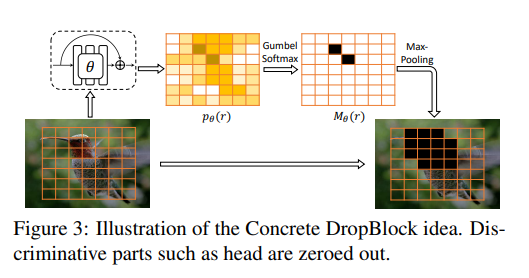
입력 이미지가 있을 때, 생성된 $|R|$개의 proposal은 모두 ROI-Pooling을 통하여 동일한 크기의 feature map $\psi_w(r) \in \mathbb R^{H \times H}$로 변환됨.

생성된 feature map은 convolutional residual block을 지나 probability map $p_{\theta}(r) \in \mathbb R^{H \times H}$로 변환됨. 여기서 $\theta$는 학습 가능한 convolutional residual block의 파라미터임.

$p_{\theta}(r)$에 spatial Gumbel-Softmax를 적용하여 hard mask $M_{\theta}(r) \in \{0,1\}^{H \times H}$을 생성함. Spatial Gumbel-Softmax 연산은 미분 가능한 approximation of sampling임. 해당 연산을 통해 $p_{\theta}(r)$이 작은 위치가 0, 아닌 부분은 1이 되도록 masking 됨.

모든 위치가 drop 되는 등의 trivial solution을 피하기 위해, threshold $\tau$를 사용하여 $p_{\theta}(r) = \min(p_{\theta}(r), \tau)$로 $p_{\theta}(r)$ 값을 조절함. 이러한 조절은 생성되는 hard mask $M_{\theta}(r)$이 sparse 하도록 보장함. 생성된 mask를 기반으로, DropBlock에서와 같이 mask 주위(0 주위)의 feature를 모두 drop 하고 feature를 normalize 함.

정리하자면, Concrete DropBlock의 목적은 입력 feature map에서 가장 discriminative point를 찾아 해당 point 주위를 전부 drop 하는 것임.

Discriminative point를 찾기 위해 convolutional residual block을 사용하며, block의 output인 probability map $p_{\theta}(r)$ 의 값이 작을수록 해당 point는 discriminative 한 것임. 즉, 기존의 classifier와 다르게 discriminative 할수록 모델의 출력 값이 작아야 함. 이러한 adversarial manner를 아래의 loss 함수로 표현할 수 있음.

$w$는 original network parameter이며, residual block parameter $\theta$는 $w$와 동시에 최적화 됨. $\theta$가 loss를 maximizing 하므로, Concrete DropBlock은 most discriminative point를 찾아 drop 할 것임. 이는 discriminative point를 지우는 것이 training loss를 증가시키는 가장 쉬운 방법이기 때문임.

Sequential batch back-propagation

이번 섹션에서는 메모리 문제를 다루기 위한 새로운 역전파 알고리즘에 대해 알아봄. 일반적인 역전파 알고리즘은 forward pass의 모든 중간 activation을 저장하여, 이후 그래디언트를 계산할 때 저장한 activation을 재사용함.

이러한 방법은 효율적이긴 하지만 많은 메모리를 필요로 함. 특히, Object detection에서 ROI-Pooling 이후의 activation은 $1 \times CHW$에서 $R \times CHW$개로 급격하게 증가함.

본 논문에서 제안하는 Seq-BBP는 Neck module의 가중치를 업데이트할 때 사용됨. Neck의 가중치를 업데이트할 때 ROI-feature 들을 sub-batch로 나누어 가중치 업데이트를 한 번에 하지 않고 연속적으로 진행함.

자세한 것은 논문 참조.

Experiments

COCO 2014, VOC 2007 & 2012 데이터셋을 사용하였음. 기본적으로 backbone에는 VGG16을 사용하여 VGG16을 사용한 기존의 연구와 성능을 비교함. ResNet 또한 사용하였음.

MIST 알고리즘의 $p$는 0.15, IoU는 0.2를 기준으로 사용함. Concrete DropBlock의 경우 $\tau=0.3, H=3$을 사용함.

Overall performance

아래의 Table을 통해 모델 성능을 확인할 수 있음.

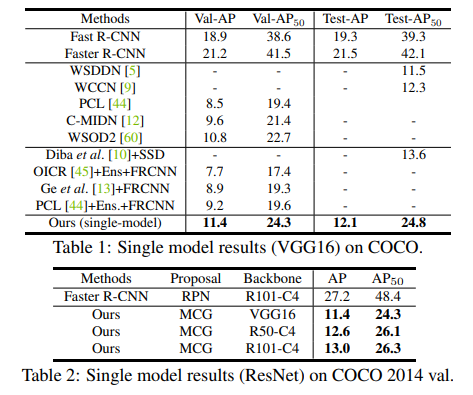
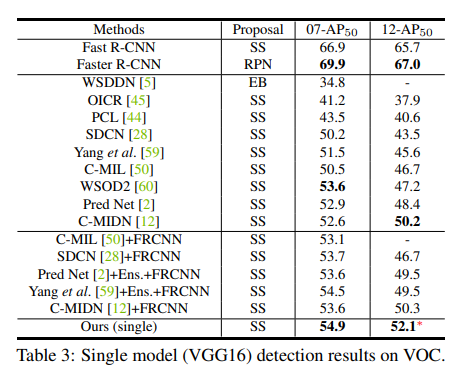
본 논문에서 제안하는 single model이 다른 아키텍처에 비해 좋은 성능을 가지고 있음을 확인함.

기존의 아키텍처 대비 좋은 성능을 달성하기는 하였지만, supervised learning 기반의 Fast / Faster R-CNN과의 성능 차이는 아직까지도 많이 나는 것을 확인함.

지금가지, WSOD에서는 메모리 문제로 인해 ResNet 모델을 사용하지 않았음. Table 2를 통해 ResNet backbone이 VGG16 backbone보다 더 나은 것을 확인할 수 있음.

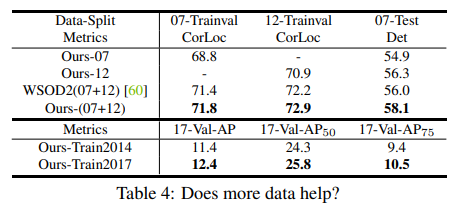
훈련 데이터가 증가할수록 WSOD framework의 성능이 향상되는지 실험함. 그 결과는 위의 Table 4와 같으며, 훈련 데이터가 증가할수록 모델의 성능이 향상되는 것을 확인하였음.

Qualitative results

본 논문에서 제안하는 framework와 OICR 논문에서 제안한 framework를 정성적으로 비교함.

Missing Instance, Grouped Instance, Part Domination 등 WSOD의 주요 문제로 제안한 3가지의 문제를 보다 잘 해결하였음을 확인함.

아래 Figure 9는 객체 탐지 성공과 실패 사례를 보여줌.

Ablation study, analysis of sequential batch BP 등 추가적인 실험 내용은 원본 논문을 참고.