Unsupervised Feature Learning via Non-Parametric Instance Discrimination(NPID) Review
cv_paper_reviews

1. Abstract & Introduction
-
이 논문의 주제는 ImageNet의 object recognition에서 나왔다고 한다.
Figure 1에서 볼 수 있듯이 레오파드에 대한 top-5 classification error를 보면, 레오파드와 비슷하게 생긴 제규어나, 치타와 같은 동물들의 softmax값은 높게 나온다. 반면에 레오파드와 전혀다른 서랍이나 보트는 softmax의 값이 매우 작다. 이를 인공지능 모델이 이미지의 유사성을 학습할 수 있다고 본 것이다. 따라서 논문에서는 이를 이용해서 같은 종류의 이미지는 서로 유사성을 학습하고, 다른 종류의 이미지는 잘 구별하도록 학습하는 시도를 했다.

-
하지만 이 실험을 진행하는데 있어서 ImageNet 데이터셋의 class 개수가 너무 많다는 문제가 있었다. 클래스의 개수가 바로 traing set의 개수이기 때문이다. 이를 해결하기 위해 논문에서는 noise-contrastive estimation과 proximal regularization을 사용했다고 한다.
-
이 논문에서는 파라미터 없이 학습과 테스트를 진행하는 방법을 사용했다. 즉, 각 이미지의 특징들이 memory bank에 저장되고 테스트는 knn을 기본으로 하여 진행한다.
-
결과적으로 성능이 좋고 나름 가벼운 모델을 만드는데 성공했다고 한다.
3. Approach
-
이 논문의 목표는 인간의 개입 없이, 인 함수를 만들어내는 것이다. (는 이미지 input, 는 이미지의 feature를 나타낸다.) 따라서,는 x, y의 거리가 가깝면 이는 x, y가 서로 유사점이 많다는 것을 나타낸다.
-
또한, 하나의 이미지를 하나의 케이스로 정의하여, 각각의 이미지를 구별(혹은 비교)하는 방식으로 모델을 학습하였다.
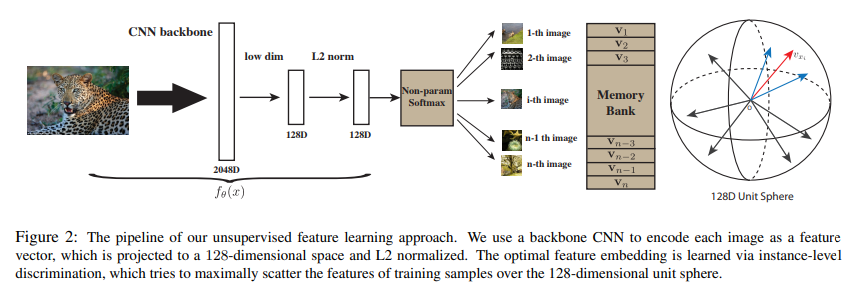
3.1) Non-Parametric Softmax Classifier
Parametric Classifier.
- n개의 이미지를 학습한다면,n개의 x에 대하여 이 성립한다. 이를 통해 x가 i클래스로 구별될 확률은
equation (1)로 나타낼 수 있다.
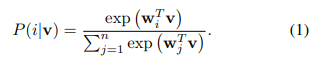
- 그러나 이 방법은 weight를 이용해서 확률를 구하는 방법이기 때문에 처음에 목표했던 다른 이미지들과의 비교를 할 수 없는 방법이다.
Non-parametric Classifier.
- 위의 문제점을 해결하기 위해 non-parametric classifier를 사용하였는데,
Equation (2)처럼 weight()대신에 를 식에 넣었다.
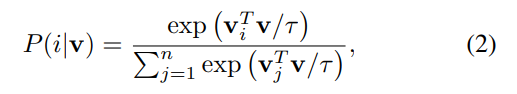
- 이를 위해서 CNN이 축출한 이미지의 feature를 L2 normalization을 적용하였고, 결과적으로 의 크기는 전부 1이 된다. (
Figure 2 참조) 또한 는 temperature parameter로, 벡터의 분포가 한 곳으로 집중되는 정도를 조절한다고 한다. - 따라서 이를 이용한 학습의 목표는 joint probaility를 최대로 하거나,
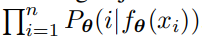
Euqation (3)을 최소화 하는 방향으로 진행해야한다.
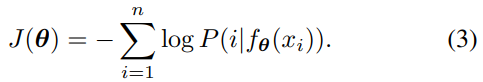
Learning with A Memory Bank
-
를 계산하기 위해서는 모든 이미지의 특징 벡터인 가 필요하다. 하지만 이를 계산하기 위해서 모든 이미지의 representation을 매번 계산하는 번거로움을 개선하기 위해 Memory bank라는 개념을 도입하였다.
-
를 memory bank로, 로 정의하자. 학습동안 와 안의 파라미터 는 SGD를 통해 업데이트 된다. 그렇다면 이 때 업데이트 된 는 안에서 대응되는 벡터 로 치환된다.
-
이런 방식으로 학습을 진행하면, 이미지의 특징 벡터로 학습을 하기 때문에 weight와 gradient를 저장할 필요가 없고, 큰 데이터에서도 모델이 잘 학습할 수 있다.
3.2) Noise-Contrastive Estimation
-
Equation (2)처럼 softmax를 계산하게 된다면, 엄청나게 많은 데이터 셋에 대해서 학습을 하기 어렵다는 단점이 있다. 이를 해결하기 위해 Noise-Contrastive Estimation을 사용했다고 한다.
(이 아래의 자세한 설명은 정확히 이해하지는 못했다 ㅠㅠ) -
일단 noise distribution이 이라는 가정과, noise sample이 data sample보다 m개 만큼 더 있다는 가정을 한다. 그렇다면 특징을 가진 sample 가 distribution에 있을 확률은
Equation (6)와 같고, 이 논문의 모델 학습 목표는 negative log-posterior distribution of data and noise sample을 최소화 하는 것이므로 이는Equation (7)을 최소화 시키는 것과 같다. 이때 는 에 대응되는 feature를 나타내고, 는 다른 이미지의 특징을 나타낸다. 이 , 은 memory bank V에 포함되어 있는 벡터이다.
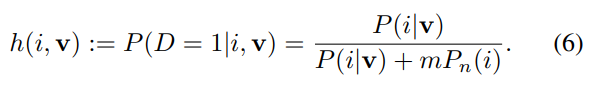
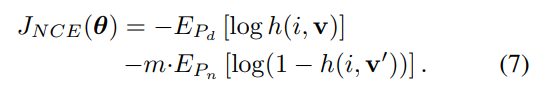
-
Equation 4의 Z을 구하는 것도 계산량이 많기 때문에 이를 줄여주는 작업을 했다. 바로 Monte Carlo approximation을 사용하였는데 {}는 데이터의 랜덤 표본을 의미한다고 한다.
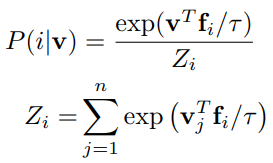
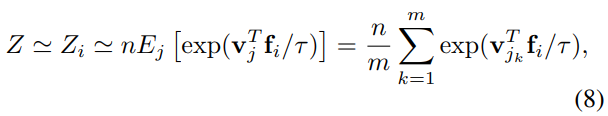
3.3) Proximal Regularization
- 이 논문의 학습 방식은 하나의 클래스에 여러가지 데이터셋이 있는 것이 아닌 각각의 데이터 셋을 하나의 클래스로 보는 방식이다. 이 때문에 학습할때 학습과정에서 많이 불안정하고 이를 개선하기 위해 proximal regularization을 도입했다.
- proximal regularization을 도입한 loss function은
Euqation (9)과 같은데, 이 함수는 기존의 loss에 현재 iteration t의 memory bank와 이전 iteration t-1의 memory bank의 차이를 더해주겠다는 의미이다. 이 proximal regularization의 값은 시간이 갈 수록 점점 줄어들 것이다.
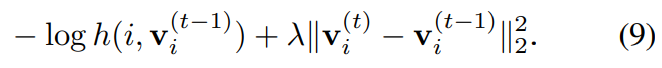
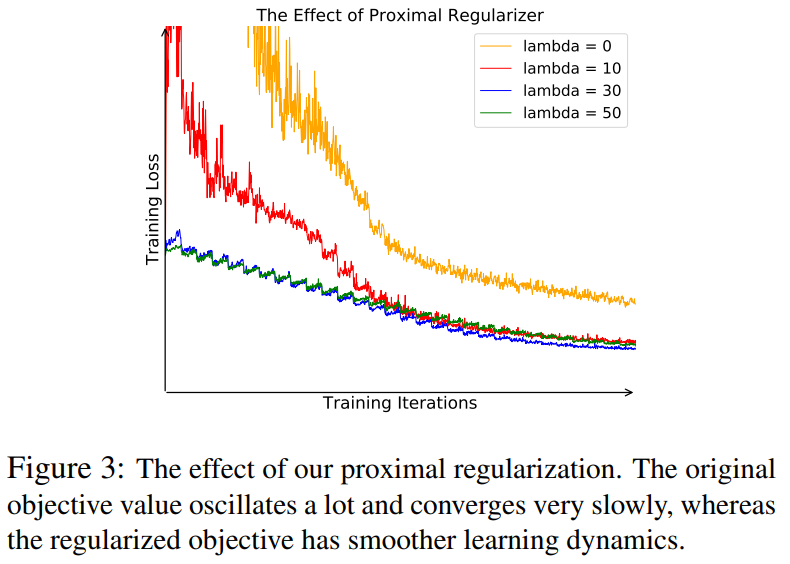
Equation(10)은 이 regularization을 도입한 식이고Figure 3을 보면 이 방법을 통해 학습 그래프가 진동하는 정도를 많이 개선한 것을 관찰할 수 있다.
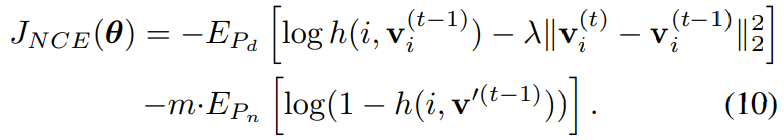
3.4) Weighted k-Nearest Neighbor Classifier
- 이 부분은 test 이미지를 넣었을 때 이미지의 클래스를 정할 것인지에 대해 설명한 부분이다. 일단 test용 이미지가 들어오면 이 이미지의 feature를 계산한다. 이 feature를 통해 cosine similarity를 구할 수 있는데 이때 memory bank에서 유사도가 높은 k개의 벡터를 뽑는다. 그 후 k개의 벡터에서 weighted voting을 통해 test 이미지의 클래스를 결정하는 방식이다.
참조
