DeepAR Paper Review + DeepLearning Foundation

이성준·2023년 1월 23일

BPTT DeepAR DeepLearning LSTM RNN TimeSeriesForecasting paper_review

PaperReview

목록 보기

1/7

이번 블로그는 원래 ARIMA SARIMA를 올려야 하는데 논문 작성에 필요한 내용들을 다시한번 정리할겸 해서 순서를 조정하기로 했습니다 혹시나 ARIMA나 SARIMA의 내용을 알고 싶은 분들은 dsd0919@naver.com 으로 메일 주신다면 궁금하신 내용 공유하길 바랍니다 !
이번 블로그는 DeepAR에 관한 블로그로 처음 읽었었던 논문이기 때문에 논문을 읽기전에 쌓아야 했던 지식들을 하나 둘 찾아서 기록해 두었습니다 그것들과 함께 논문내용을 번역 및 제 생각을 담아 공유하고자 합니다! 한마디로 말해서 딥러닝에 관해서 잘 모르시는 분들이 읽으셔도 조금씩 내용을 찾아서 본다면 쉽게 이 블로그를 이해하실 것 이라고 기대합니다 !
P.S 중간에 설명을 위해 직접 그린 그림이 있음을 알립니다
또한 틀린 설명이나 내용의 공유를 하고 싶으신 분들은 메일 주시기 바랍니다!

개요

딥러닝 Basic
1.1. 딥러닝 학습과정
1.2. 활성화 함수
1.3. 목적함수
1.4. Optimizer 와 Gradient Descent
1.5. BackPropagation for matrix computing
1.6. 추후 알아볼 사항
딥러닝 모델
2.1. RNN
2.2. LSTM
Deep AR 논문 review

1. 딥러닝 Basic

1.1 딥러닝 학습과정

딥러닝 학습과정

데이터 준비
→ 데이터 준비 후 누락 값 이상치 제거 등의 과정을 거친다
모델 정의:
→ 신경망을 생성한다 일반적으로 Hidden Layer의 개수가 많을수록 성능이 좋아지지만 과적합이 발생할 확률이 높다.
또한 활성화 함수, 목적 함수, Optimizer등을 선택한다
트레이닝:
→ 트레이닝은 forward propagation과 backward propagation 과정으로 나뉜다

Forward propagation 과정에서 우리는 우리가 준비한 데이터를 input layer에 값으로 집어넣고 여러 가중치와 hidden layer에 활성화 함수를 거치면서 우리는 Output layer에 도달하게 된다 이때 목적함수를 최소화 하는 방향으로 가중치를 업데이트 하는 backward propagation 과정을 거치면서 가중치를 업데이트 한다

Multi-Layer Perceptrons

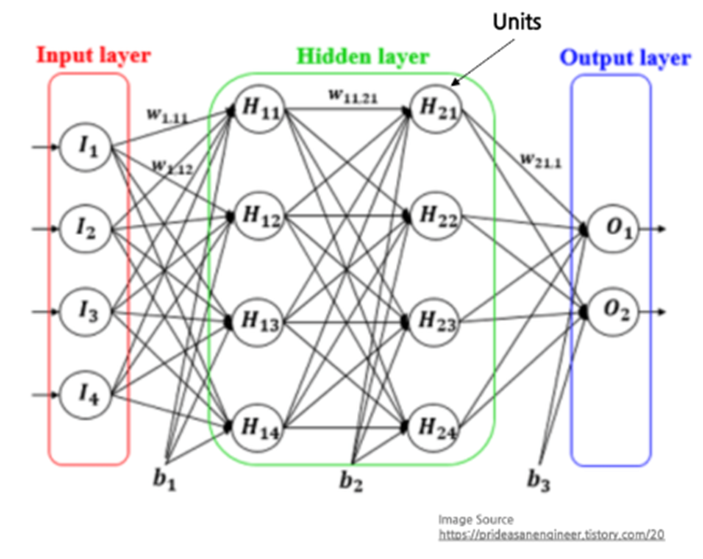
1.2 활성화 함수(activation function)

MLP를 하나 가정하자

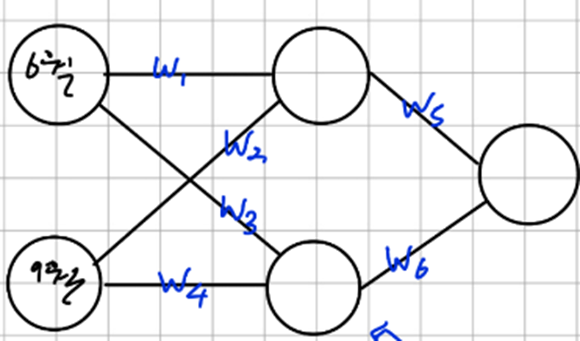
다음과 같은 경우 hidden layer를 추가한 의미가 없어진다

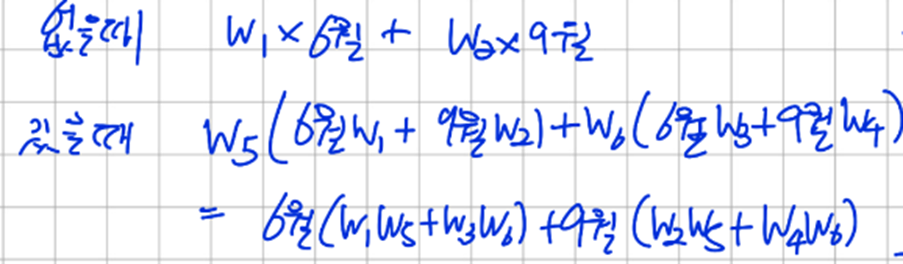
다음과 같이 activation function 을 사용하지 않으면 Hidden Layer를 추가해 모델을 깊게 만든 이유가 사라진다 즉, 모델 자체가 선형적이라 선형적인 예측만 가능하다.
따라서 이런 문제를 해결하기 위해 활성 함수로 비선형 함수를 사용하여 비 선형적인 예측도 가능하게 했다

다양한 Activation function의 종류와 장단점

Sigmoid

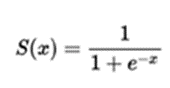
장점-> activation func으로서의 장점은 없다
단점->
```
가. Saturation 현상
```
좌우로 접선의 기울기가 0이 되는 지점이 -6,+6만 되어도 시작되어 back propagation을 통해 업데이트 할 때 dL/dw가 0이 되므로{Sigmoid function 그림 참고} w의 업데이트가 없어지는 Saturation현상이 발생한다
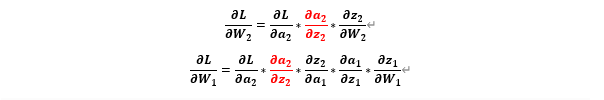
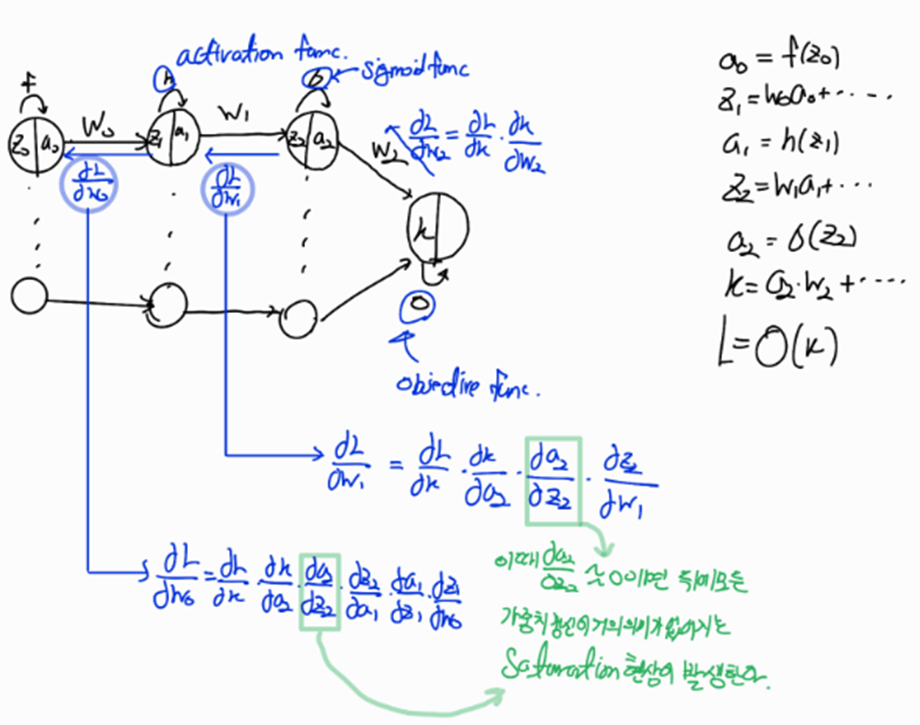
```
나.	exp연산이 들어가므로 연산이 느리다

다.	Zig Zag 업데이트 현상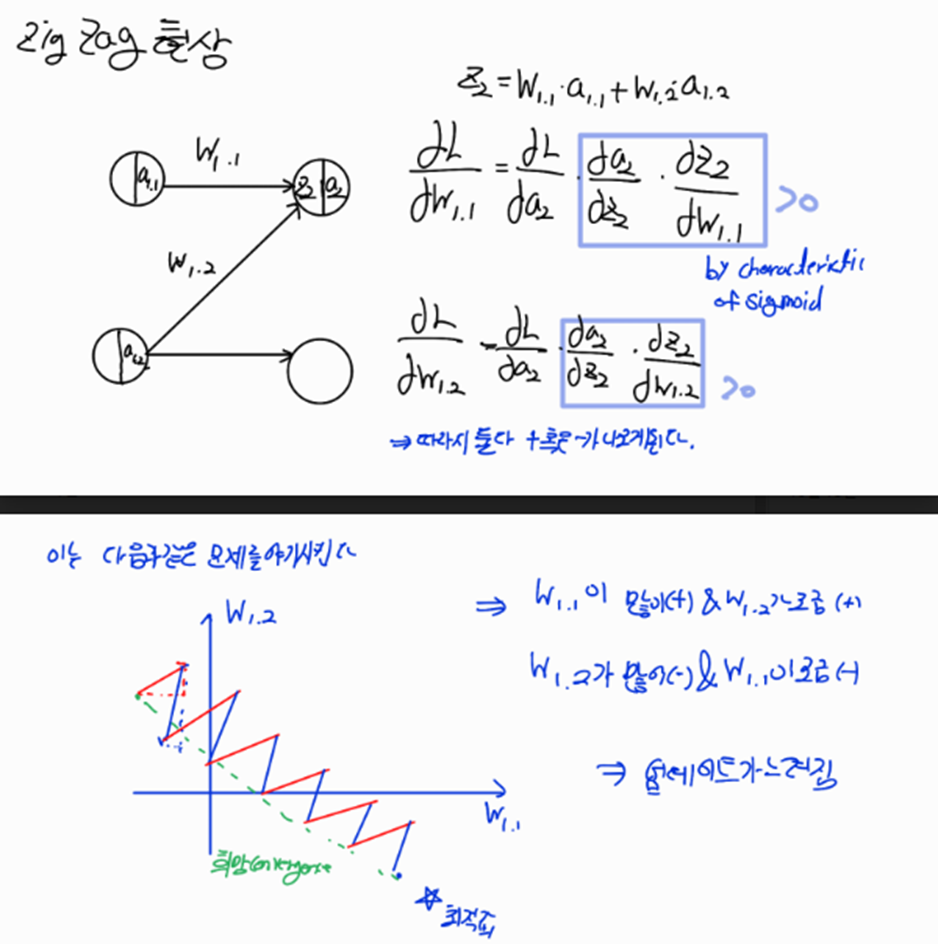
```
위와 같은 문제를 해결하기 위해서 나온 activation function은 바로
Tanh(hyperbolic tangent)

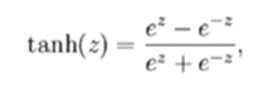
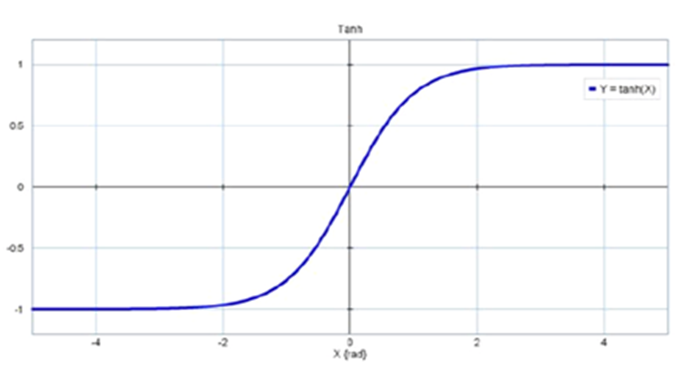
장점: 결과값이 -1~1 사이기 때문에 zigzag 현상이 덜하다
단점: 변함없이 saturation 현상이 있어 w업데이트가 멈출 수 있다

ReLU(Rectified Linear Unit):

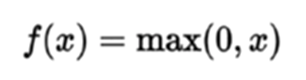
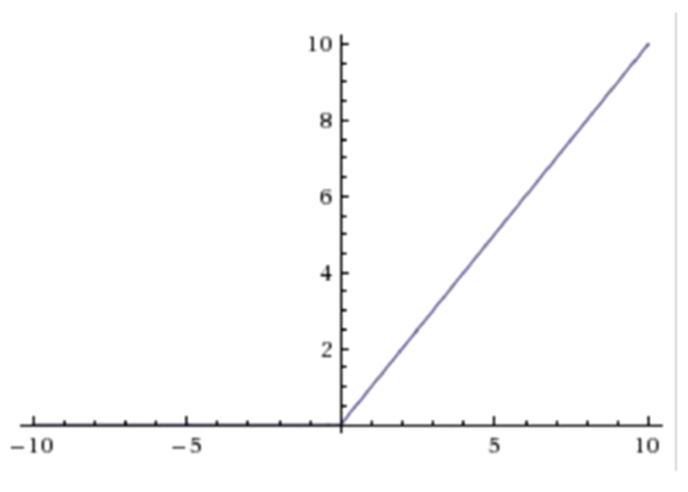
장점: saturation 되는 부분이 2군데에서 1군데로 줄었다(<0인 부분) / Exp 연산이 없어서 연산이 빠르다/ 수렴속도가 sigmoid/tanh에 비해 빠르다
단점: ReLU의 Output 결과값이 0 or (+) / 편미분 값도 0 or 1이기 때문에 zigzag현상이 생긴다
[참고]https://nittaku.tistory.com/267

1.3. 목적함수(Objective function)

이후에 교수님과의 미팅에서 논의 해본 결과 실제 Field에서는 구분없이 쓴다고 합니다. 하지만 내가 지금 쓰고 있는 블로그에서는 구분하는 것이 이해에 도움이 되기에 참고하길 바랍니다!

Loss Function
Input(x)에 대한 예측값 y(hat)과 실제 label값(y) 사이의 오차를 계산하는 함수이다
예로 Linear regression의 경우 Loss Function으로 최소제곱오차를 사용한다

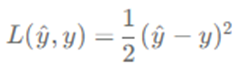
즉, 하나의 input data에 대해 오차를 계산하는 함수를 loss function이라고 한다
Cost Function
모든 input dataset에 대해서 오차를 계산하는 함수를 Cost Function이라고 한다
따라서 Cost Function은 모든 input dataset에 대해 계산한 Loss function의 평균값으로 구할 수 있다

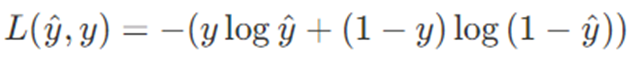
Cross entropy
→분류에서 많이 사용하는 loss function으로 정답 클래스에 해당하는 스코어에 대해서만 로그합을 구하여 최종 Loss를 구한다( Soft max function이후에 사용함)

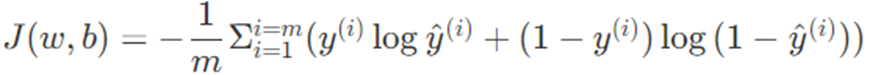
위에 Loss function에 상응하는 Cost function이다 모든 데이터에 대한 Loss를 평균내 Cost를 계산할 수 있다
Objective Function

MLE (Maximum Likelihood Estimation)
우리는 MLE를 Object function으로 쓰기 전에 어떤 통계모델이 데이터 생성의 과정을 가장 잘 표현하는가를 먼저 생각 해야 하고 이렇게 선택된 통계모델의 파라미터를 조절함으로써 최대우도를 얻기 때문에 매우 중요하다
이렇게 통계모델을 선택할 때는 도메인에 대한 지식이 상당히 중요하고 이에 맞는 통계모델을 선택할 수 있어야 한다.
우리는 Likelihood Function을 생각해 볼 수 있는데 이것은 분포의 Probability Density Function(p.d.f)으로 나타난다
Gaussian Probability Density Function

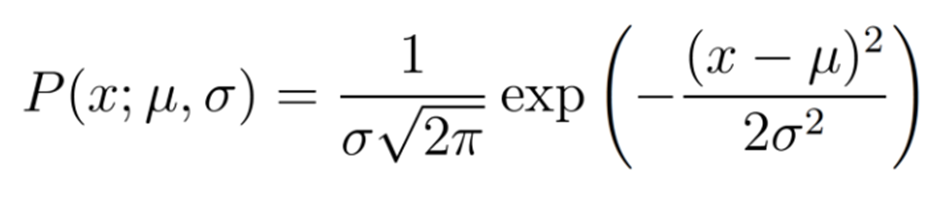
여기서 쓰는 semicolon의 의미는 확률분포의 parameter 들을 강조하기 위해 사용했다{논문에서 자주 표현됨}

예를 들어서 우리가 Gaussian Distribution이라고 추측하고 data가 9,9.5,11이 나왔다고 가정하자 이때의 likelihood는 다음 곱과 같다

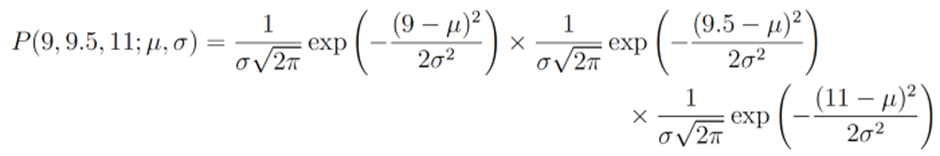
이때 우리는 이 Likelihood를 최대화 하는 평균과 sigma를 찾아야 하는 것이다
우리는 위의 방정식을 log를 사용하면서 log-likelihood를 찾을 수 있다(미분의 용이성에 의해)

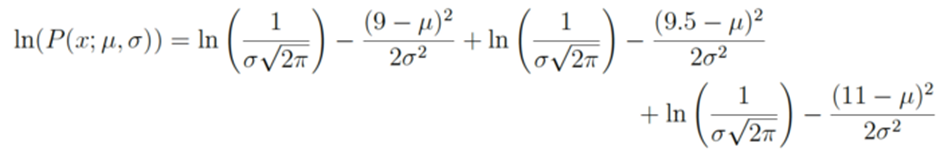
실제로 log-likelihood가 더 많이 쓰인다

우리는 선택된 확률분포가 maximum Likelihood를 갖도록 파라미터를 조정하는 backpropagation과정을 거치게 된다
이번 논문에서는 Negative Binomial Distribution을 사용한다

1.4. Optimizer와 Gradient Descent

[참고]
https://dbstndi6316.tistory.com/297
https://www.youtube.com/watch?v=uJryes5Vk1o

딥러닝 학습시 최대한 틀리지 않는 방향으로 학습해야 한다(→loss를 줄이는 방향으로)
이때 loss의 최솟값을 찾아가는 것을 최적화(Optimization)이라고 하고 이를 수행하는 알고리즘이
최적화 알고리즘(=Optimizer)라고 한다

따라서 우리가 지금부터 얘기할 Gradient Descent는 어떤 알고리즘이고 여기에 사이즈를 추가한 것이 Batch Gradient Descent/Mini-Batch Gradient Descent이다
Optimizer의 종류는 다음과 같다

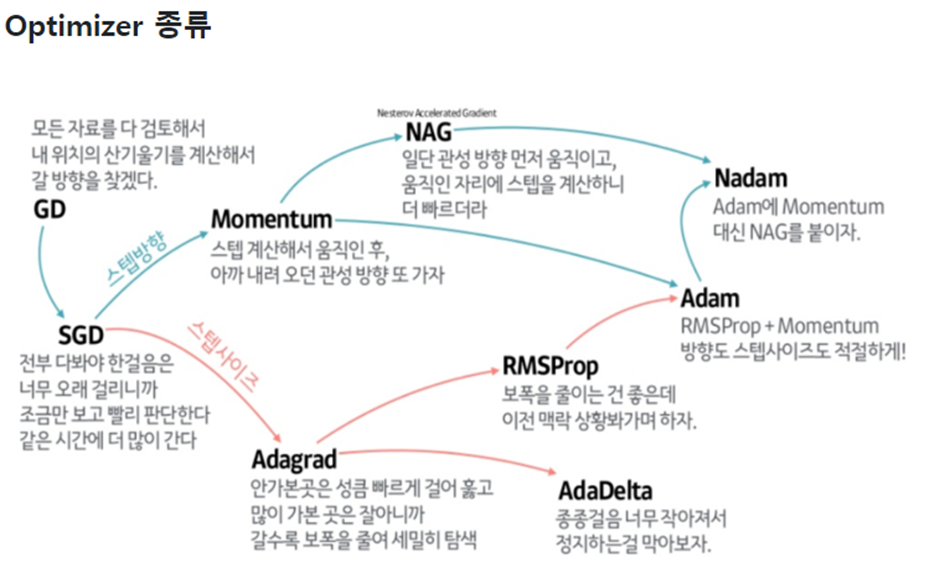
Adam을 제일 많이 사용한다

Gradient Descent

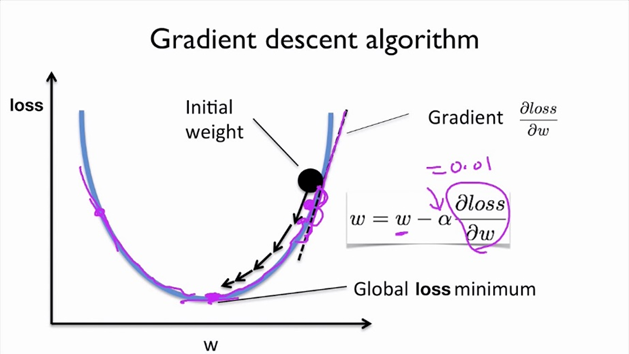
우리는 위의 사진에서 weight에 따른 loss function을 볼 수 있다. 우리는 Backpropagation과정에서 weight를 loss function이 감소하는 방향으로 업데이트 시켜야 하는데, 이때 loss function을 w로 partial derivative을 한 것이 바로 Gradient라고 정의하고 한번에 다가갈 step을 learning rate라고 한다. 여기서 Learning rate를 최적화 해 나가는 방식을 Optimizer라고 부른다

learning rate가 이상적인 경우
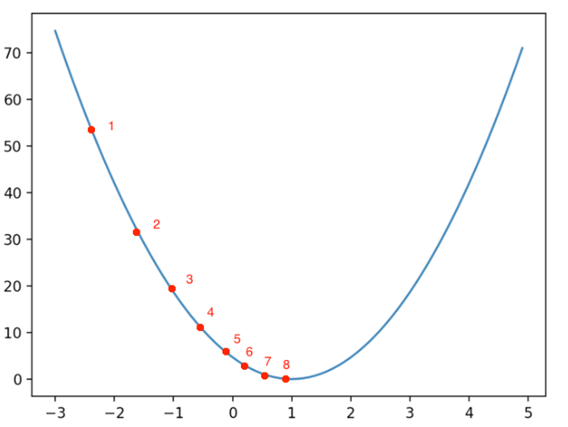
learning rate가 클 경우

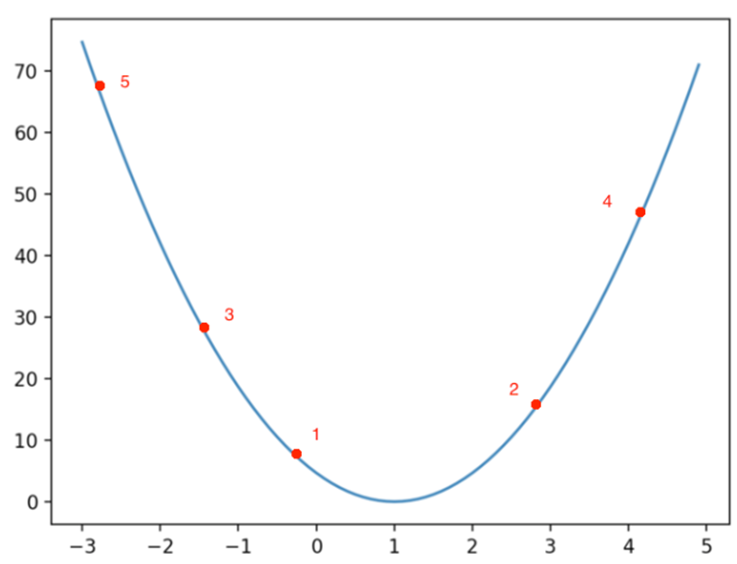
→ learning rate가 크다면 다음과 같이 minimum값에 수렴하지 못하는 현상이 생긴다
learning rate가 작을 경우

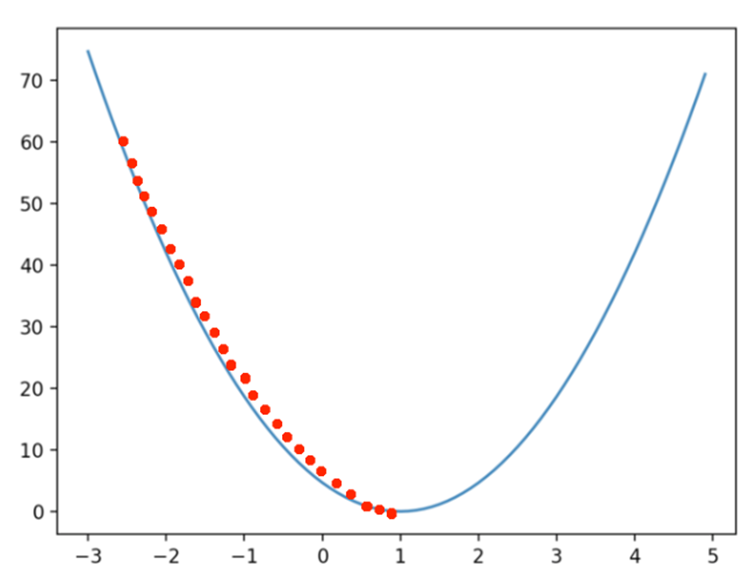
수렴하긴 하지만 최종값으로 찾아갈 때까지 너무 많은 반복을 수행해야한다 즉, 학습속도가 지나치게 느려진다
https://wikidocs.net/152765
↑ Momentum과 Adam등을 참고하면 좋을 자료 이다

이제 데이터 양에 따라 Gradient Descent의 방법을 나눠보자!

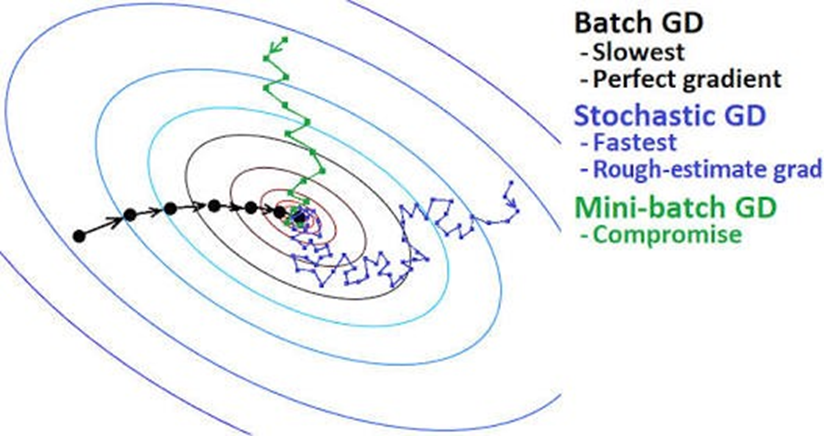
(1) Stochastic Gradient Descent(SGD)
우리의 데이터가 100만개 있다고 가정해보자 우리는 이 데이터를 한 sample씩 Neural Net에 집어넣을 수 있다. 하지만 이렇게 되면 100만개의 데이터를 모두 처리하는데 시간이 많이 걸리고 비효율이 따른다. 따라서 우리는 Stochastic이라는 말을 붙여서 이중에 랜덤으로 몇 개의 Sample을 선택해서 최솟값으로 수렴하도록 하는 것이다.
랜덤으로 선택하는 방법은 단순하게 데이터 Sample을 섞어주면 된다.
확률적 경사 하강법은 극단적으로 노이즈가 많을 수 있지만 평균적으로는 좋은 방향으로 가게 된다 .

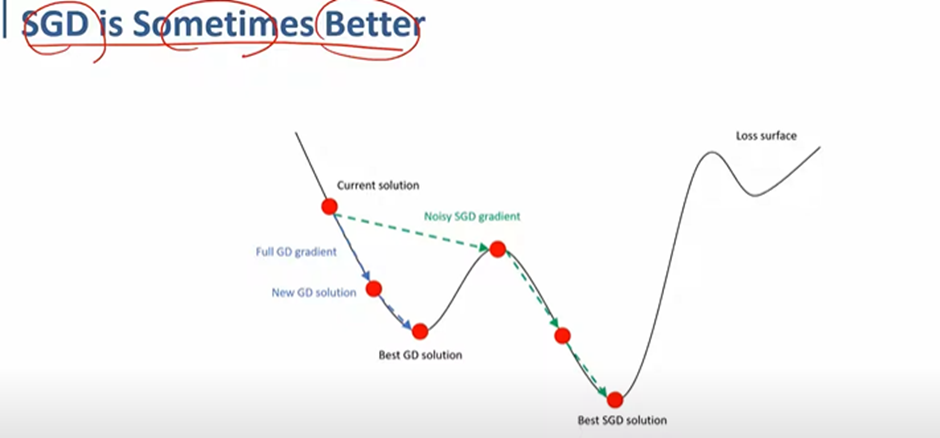
위와 같이 원래 같으면 Local minimum에 빠지는 것을 막아 줄 수도 있다.

Batch Gradient Descent

배치 경사 하강법(Fully Batch Gradient Descent)은 모든 반복(epoch)에서 훈련 sample들을 묶어서 하나의 행렬로 만들어 훈련을 진행하고 각각의 epoch마다 비용이 감소하길 기대한다
우리는 Batch Gradient Descent를 진행하면 안정적으로 Cost Function값이 감소하는 것을 알 수 있는데 하지만 위에서 우리가 가정한 100만개의 샘플에 대해 한번에 계산을 시도하다 보니 하나의 epoch마다 너무 많은 Computing 자원을 소모하게 되고 시간이 오래 걸린다 따라서 작은 훈련 세트에 대해서는 괜찮지만 큰 훈련 세트에 대해서는 오랜 시간이 필요하다
하지만 한번의 epoch에 우리가 가지고 있는 모든 샘플을 사용하므로 데이터의 일관성(?)이 유지가 돼서 Smooth하게 Cost Function에 최솟값에 수렴할 수 있다

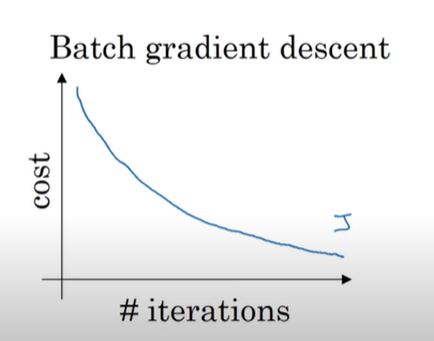
따라서 우리는 이 둘 사이에 적당한 크기의 Sample을 뽑는 경우를 선택할 수 있다

Mini-Batch Gradient Descent
우리는 한번에 Neural Net에 넣을 데이터 Sample의 크기를 m으로 정할 수 있다
이렇게 Batch Size를 정하고 우리는 데이터 샘플을 섞어서 mini Batch Size만큼 데이터 샘플을 뽑는다 그 이후 이를 Neural Net에 넣어 주고 Cost Function을 최소화하는 Gradient를 찾아내 가중치를 업데이트 시켜준다.

Mini batch gradient descent는 다음과 같이 수렴하는 것을 볼 수 있는데,
위와 같이 진동하는 이유는 첫번째 샘플 mini-batch에 대해서는 cost가 낮은데 우연적으로 outlier가 포함된 다음 mini-batch이고 따라서 cost가 높아진 것이라고 설명 할 수 있다

그렇다면 적절한 batch size는 어떻게 정할까

CHOOSING YOUR MINI-BATCH SIZE
If small train set : Use Batch Gradient Descent
(m<=2000)
Else
컴퓨터 메모리의 접근 방식을 생각해보면 미니 배치 크기가 2의 제곱인 것이 코드를 빠르게 실행시켜준다
64, 128, 256, 512 . . .

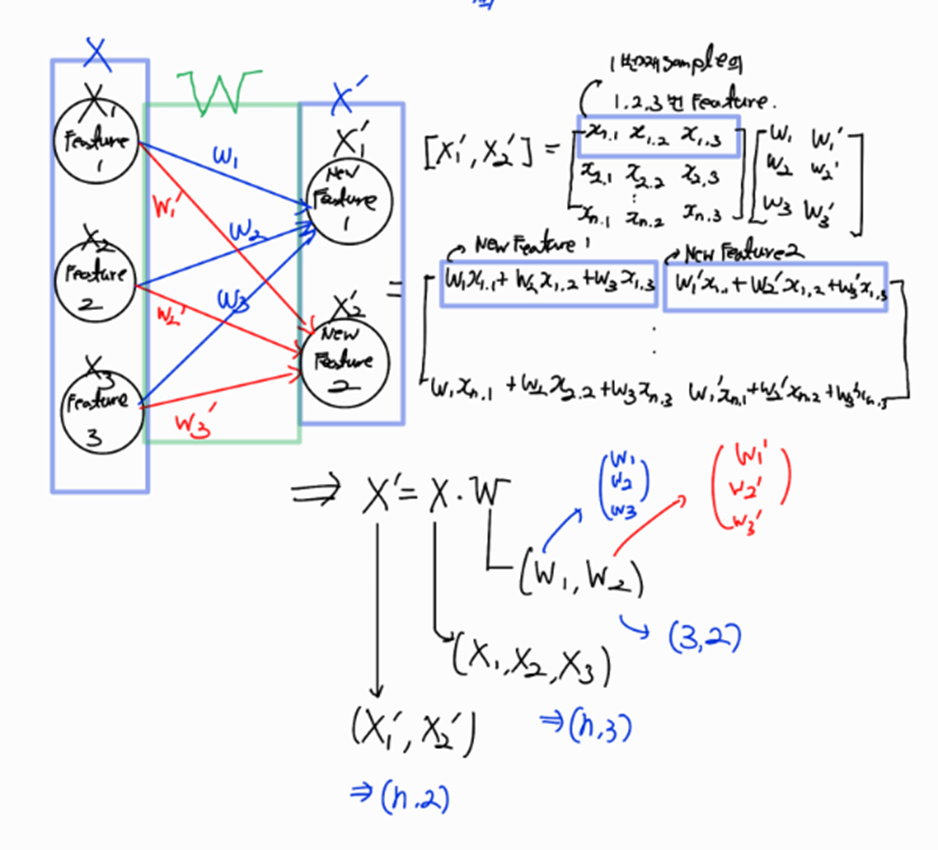
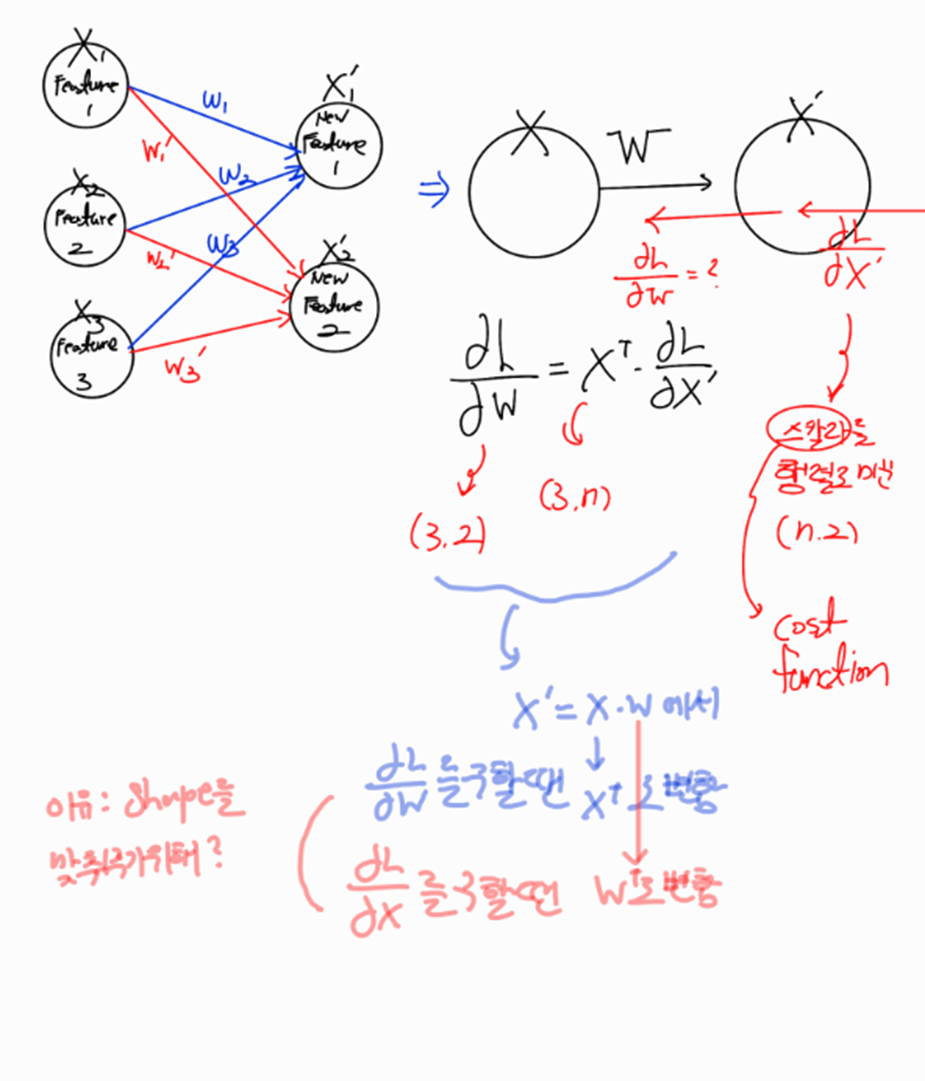
1.5. BackPropagation for matrix computing

우리는 위에서 activation Function을 다룰 때 이미 입력 데이터가 하나의 입력 sample에 대해서 Backpropagation을 진행해 봤다 이제 여러 데이터가 행렬로 입력이 될 때 Backpropagation이 어떻게 일어나는지 알아보겠다 기본 원리는 똑같지만 계산이 행렬계산 이라는 점에서 차이가 있다

2. 딥러닝 모델

출처:
https://www.youtube.com/@GlobalAcademyNIA
https://www.youtube.com/watch?v=MrQWEscdseo
https://wikidocs.net/22886
위의 강의와 자료들을 토대로 이해한 바를 토대로 작성해보겠다

2.1. RNN(Recurrent Neural Net)

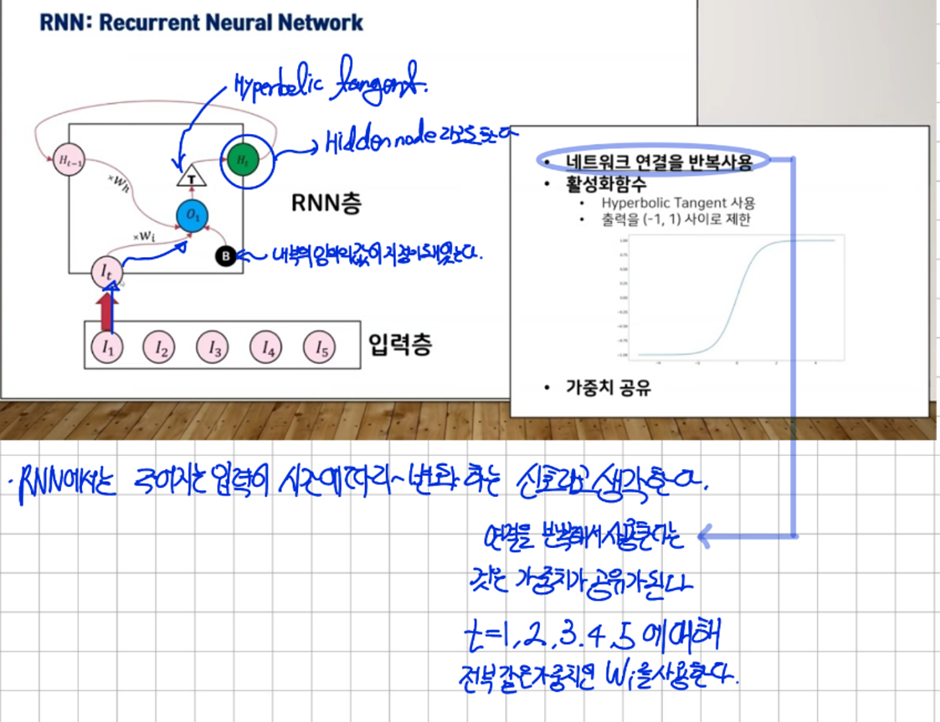
RNN에서는 메모리 셀( RNN CELL )을 도입해서 여기에서 나오는 결과값인 H_t(Hidden state)를 사용하여 이전의 결과값이 다음의 결과의 영향을 주도록 만들었다 시간에 따라서 입력이 Neural Net에 하나씩 들어오게 되고 결과적으로는 같은 RNN에 입력이 바뀌어서 들어오는 것이기 때문에 시간에 따라 가중치가 공유된다
RNN을 위에처럼 표현할 수도 있지만 펼쳐서 표현도 가능하다

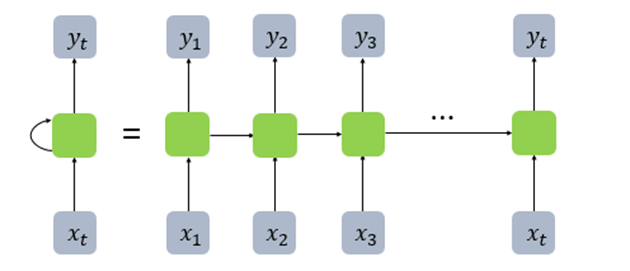
RNN에 대한 수식을 정의해보겠다

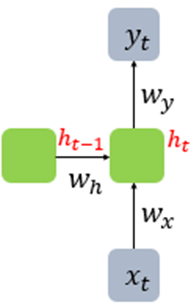
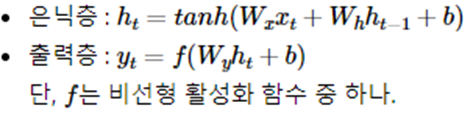
우리의 입력벡터의 차원이 d라고 하고 은닉 상태의 크기를 D_h라고 할 때 각 벡터와 행렬의 크기는 다음과 같다

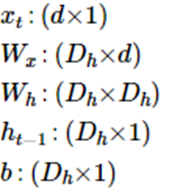
이때 d와D_h 값을 모두 4로 가정하면 hidden state의 연산이 다음과 같이 진행된다

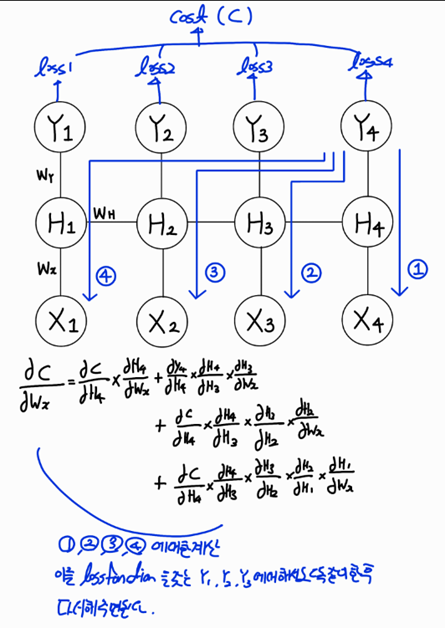
RNN의 BackPropagation(BackPropagation Through Time)[BPTT]
RNN은 기존 신경망의 역전파와는 달리 타임 스텝별로 네트워크를 펼친 후, 역전파 알고리즘을 사용하는데 이를 BPTT라고 한다 BPTT는 그래디언트가 마지막 타임스텝의 출력뿐만 아니라 손실함수를 사용한 모든 출력에서 역방향으로 전파된다.
만약 RNN의 seq2seq 모델을 생각해보자 모델의 predict까지 길이가 총 100개라고 해보자 이때 predict를 내놓는 Decoder의 길이는 10이라고 할 때 이 RNN의 길이가 길어지면 길어질수록 우리는 곱해지는 것이 계속 많아지게 될 것이고 마지막쯤 가면 거의 업데이트를 하지 않는 경우가 발생 할 것이다(Gradient Vanishing)
→ 이를 TimeSeriesForecasting에서는 Long Dependency를 capture하지 못한다고 한다

위와 같은 문제를 해결하기 위해서
Truncated BPTT가 존재한다 이를 이해하기 위해서는 RNN은 하나의 layer에 입력값이 차례대로 들어감을 유념하고 있어야한다 즉, 펼쳐져있는 RNN으로 생각하지 말아보는 것을 추천한다

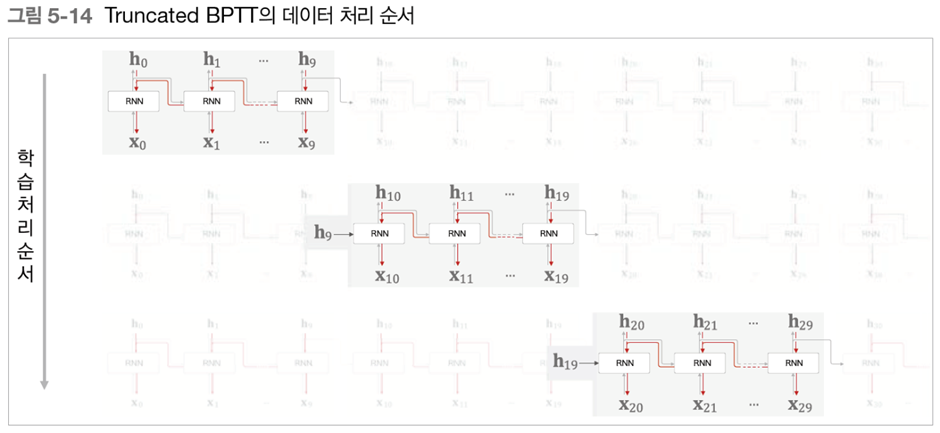
시간 순서대로 지나가면서 backpropagation을 잘라서 진행하는 것이다
첫번째 Cutting에서 가중치 업데이트-> 두번째 Cutting에서 가중치 업데이트 -> 세번째 Cutting에서 가중치 업데이트 …

2.2. LSTM(Long Short Term Memory)

기존에 단기기억만 할 수 있었던 RNN Structure에 장기기억을 담당하는 long-term memory가 추가 됐다. 이를 우리는 Cell State라고 부른다

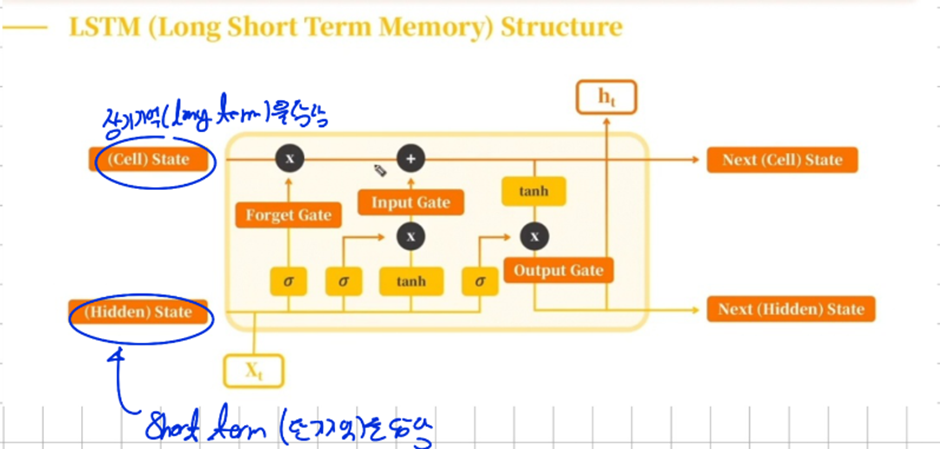
LSTM은 3가지의 Gate와 2가지의 State를 갖고 있는데 3가지의 Gate로 Cell state에 들어가는 정보의 양을 조절해주고 두가지의 State가 각각 장기기억과 단기기억을 담당하고 있다.
결과적으로 LSTM은 forget gate, input gate와 Output gate 이 3가지 Gate로 전달되는 정보의 양을 최적으로 만드는 가중치값을 찾는게 목표가 된다

가. Forget Gate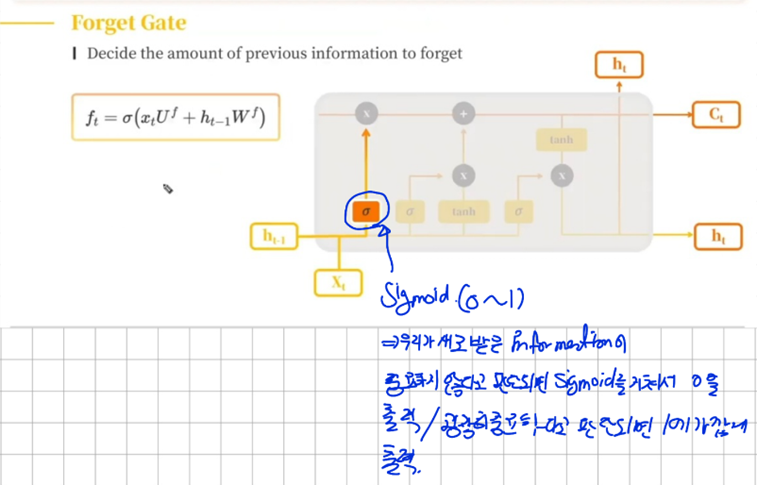

이전으로부터 받은 정보(hidden state)와 우리가 새로 입력 받은 정보를 토대로 이전의 정보를 얼마나 잊을지 결정하게된다

나. Input Gate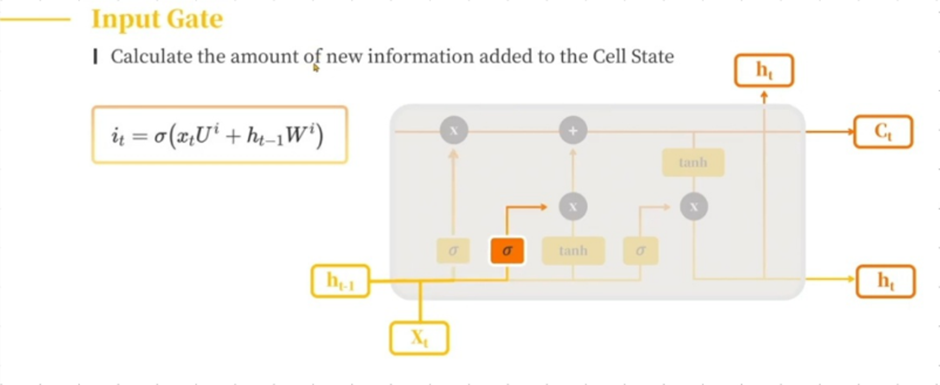

우리에게 입력 받은 정보를 토대로 우리의 입력 값을 얼마나 입력할지 결정하는 Input Gate

다. Cell State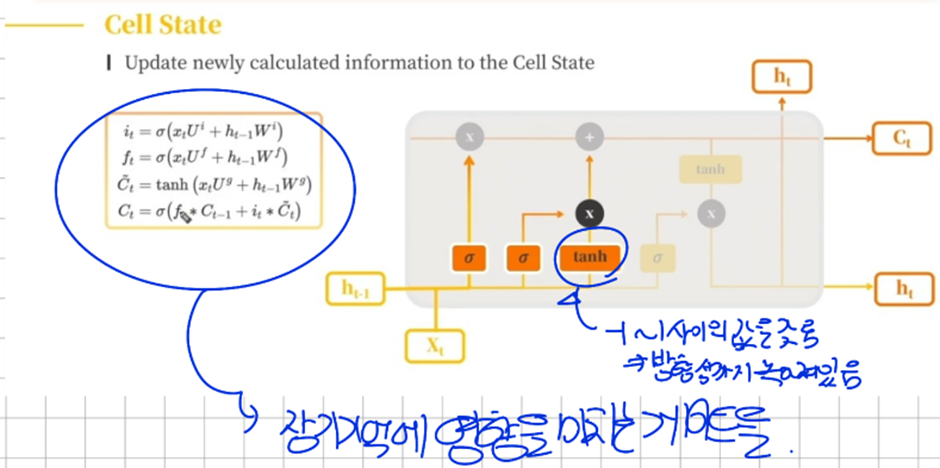

새로운 기억 셀에서는 활성화 함수로 tanh 함수를 사용해줌으로써 새로운 정보에 대해서 방향성 까지 녹여서 입력을 해주게 된다
→ tanh함수는 정보를 입력할 때 사용 Sigmoid함수는 정보를 얼마나 쓸 것인지 에 사용

라. Output Gate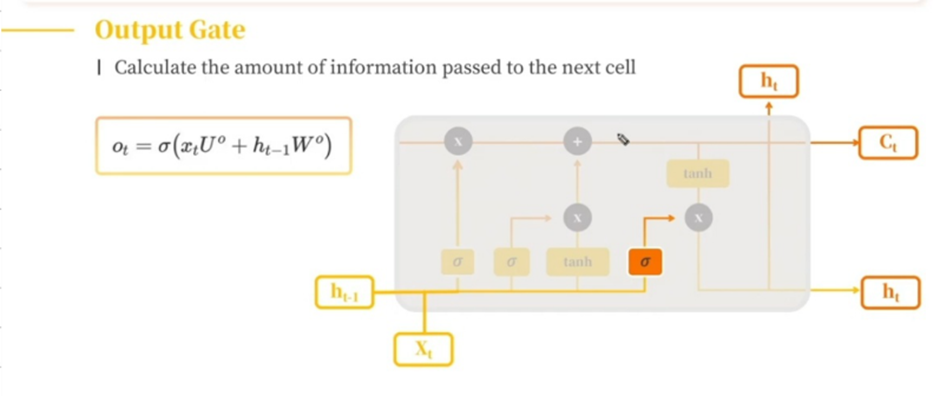

우리가 입력 받은 정보를 얼마나 다음 hidden state에 전달할지 결정하는 게이트

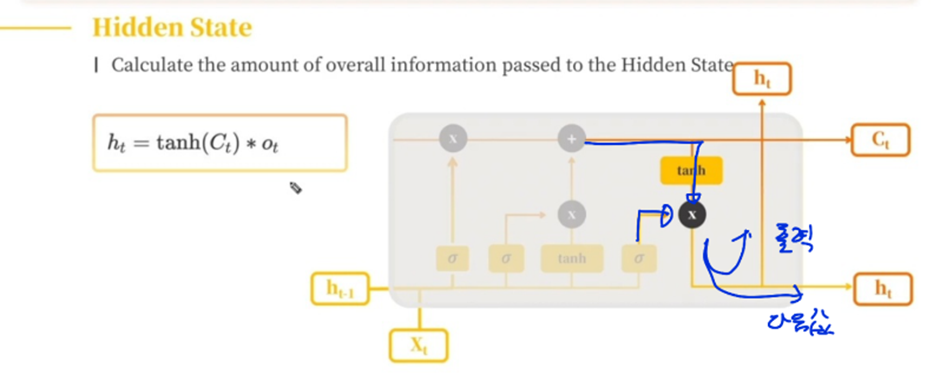
LSTM이 Gradient Vanishing이 덜 한 이유

LSTM은 Gradient Vanishing을 완전히 막는 건 아니다 단지 위의 LSTM Structure에서 보이듯이 Cell State 에서 2개연산의 역전파가 진행되는데 하나는 +라 Gradient값을 그냥 흘려 보내준다 또한 Gate를 4개 도입하면서 f, g, I, o 값이 매번 바뀌기 때문에 Gradient Vanishing이 발생할 가능 성이 적어진다 (즉 바뀌는 값이 많아진다)
위의 곱에 대해서만 Gradient Vanishing이 발생한다

Self Discussion
위의 내용을 더 자세히 알고 싶다면 다음 자료를 확인해보자
https://data-science-blog.com/blog/2020/09/07/back-propagation-of-lstm/

Paper Review에 들어가기전에
우리는 RNN을 SEQUENCE TO SEQUENCE/ SEQUENCE TO ONE 이렇게 입력값의 개수와 출력값의 개수로 종류를 나눌 수 있지만 큰 원리 자체는 동일하다

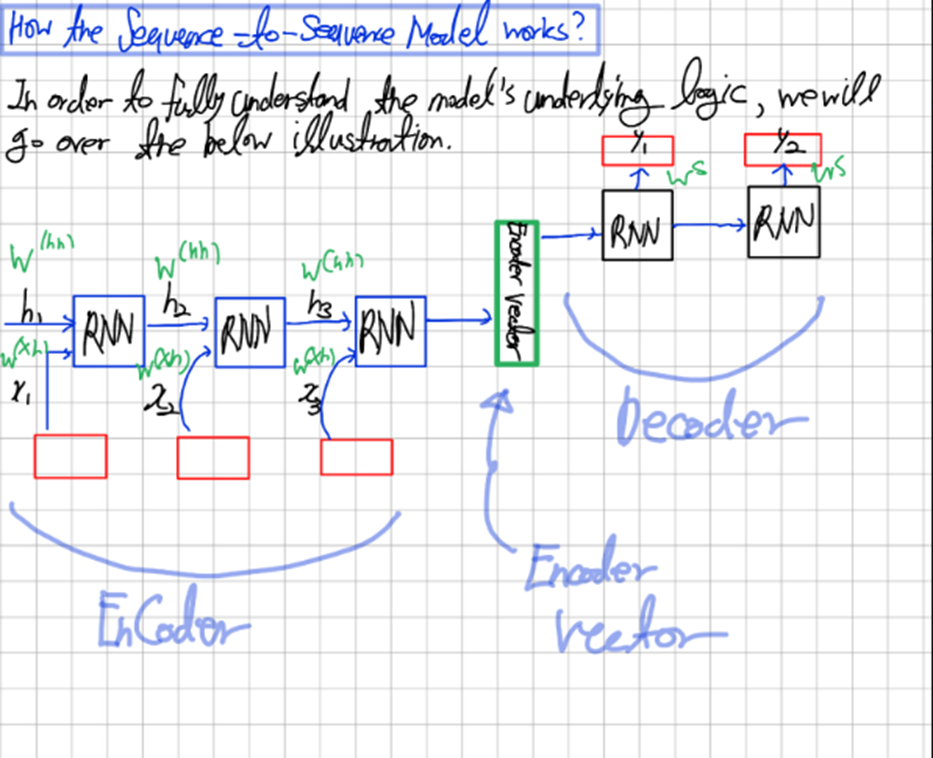
Training과정에서 Decoder에서 inference한 값들을 토대로 Cost Function을 계산하고 이를 Back Propagation한다

중간에 Encoder Vector 부분에 회로라고 읽힐 수 있지만 '최초'라고 쓴 것이다(글씨가 악필이라 죄송합니다 :(

3. Deep AR 논문 review

[Reference]
https://www.youtube.com/watch?v=okyo61ZZivA
https://arxiv.org/abs/1704.04110
INTRODUCTION
오늘날 사용하는 예측방법은 point forecasting이나 작은 그룹에 대한 예측만 할 수 있도록 개발됐다.
하지만 최근에는 다량의 서로 연관된 time series를 예측하는 문제가 대두됐다 예를 들어 거대한 retailer에 의해 제공되는 모든 상품들에 대한 수요 예측 등이 있다
이러한 예제에서 유사한 종류의 Time series 가 예측에 영향을 미칠 수 있다
유사한 종류의 Time series data를 사용하는 것은 과적합없이 모델을 더욱 Flexible하게 Fitting을 할 수 있고 Neural Network를 사용하면서 Classical Technique 들에서 요구됐던 feature engineering과 model selection 과정을 덜 할 수 있다
(이 논문이 나왔을 시점(2019)엔 딥러닝이 시계열 예측에 많이 활용되지 않았을 시점이라서 이런 언급을 함)
여기서 사용하는 Deep AR 모델은 RNN기반의 forecasting method이다.
여기서 제안하는 모델은 여러 시계열 데이터셋에 맞는 global한 모델이며 정확히 하자면 Probability forecasting problem에 대한 LSTM 기반의 RNN architecture를 갖고 있다

우리가 real-world forecasting problem으로부터 직면하는 문제는 Time series의 서로 다른 magnitude이다 이는 아래그림 자세히 설명하는데

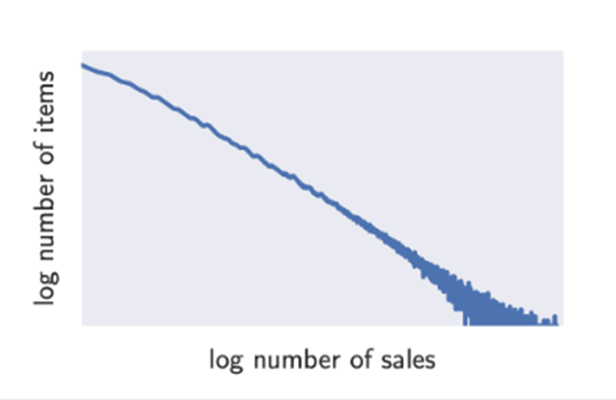
즉 많이 팔리는 물건은 매우 극소수이고 적게 팔리는 물건은 매우 많다는 것이다

MAIN CONTRIBUTION
(1) Proposing Deep-learning PB Forecasting and Handling Variable Scale Time-Series
→ probabilistic forecasting에 negative Binomial likelihood를 포함하는(목적함수로 갖는) RNN architecture를 제안한다 또 다른 크기를 갖는 Time series를 다루는 경우를 다룬다
(2) Effectiveness of Deep-learning for Time Series
→우리는 여러 real-world data에 대해 이 모델이 정확함을 보여줌으로써 시계열에 대한 modern deep learning based approach가 충분히 효과적임을 보여줄 수 있다
(현재는 딥러닝 기반의 시계열 예측은 별로 라는 인식이 있다)
Key Advantages
(1) 모델이 계절성과 Time Series 전반에 걸친 주어진 Covariates에 대한 의존성을 학습하기 때문에 서로에게 의존하는 행동과 복잡성을 포착하는데 보통 최소한의 feature engineering만 필요하다 (-> 시계열 예측에 여러 Covariate를 학습시킨다)

(2) DeepAR makes probabilistic forecasts in the form of Monte Carlo samples(중복 추출)

(3) 비슷한 item들로부터 학습함으로써 이전의 데이터가 없는 신제품의 경우에도 예측을 할 수 있다(신제품의 수요 예측)

(4) DeepAR은 Gaussian noise(Distribution)를 가정하지 않고 데이터의 통계적 성질에 맞게 다양한 Likelihood function을 포함할 수 있다

Model

시점 t에서 시계열 i의 값을 $z_{1,t}$ 로 하자
우리의 목표는 각 시계열 i에 대해서 conditional distribution( conditional probability function)을 구하는 것이다
다음과 같이 notation을 정의 한다
[Future]
→[ $t_0$ , $T$ ] : prediction Range

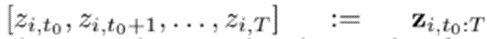
[Past]
→ $[1 , t_0-1]$ : Conditioning Range

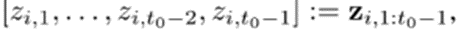
[Covariates]
$X_{i,T}$ : 우리는 Covariates를 모든 시간 범위에 대해 알고 있다고 가정한다

Training
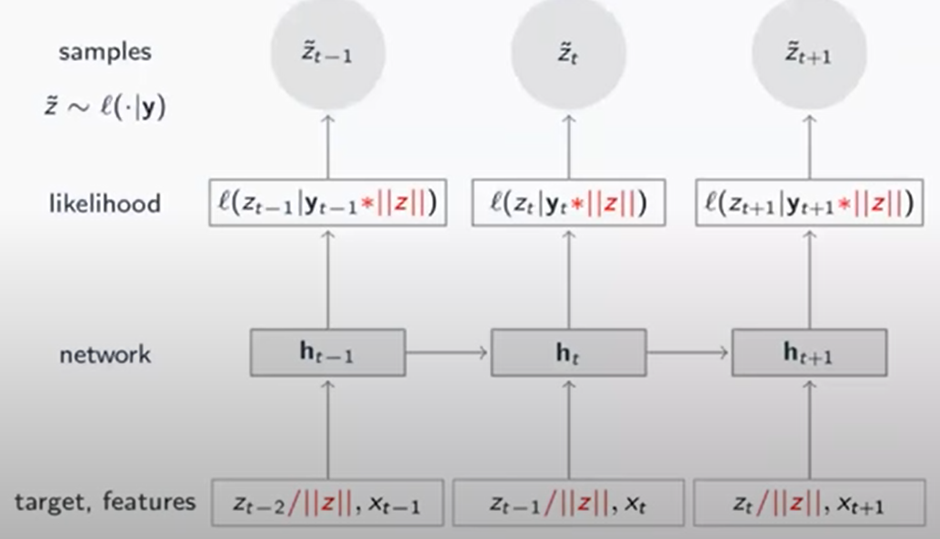
Train과 prediction의 Figure는 다음과 같다

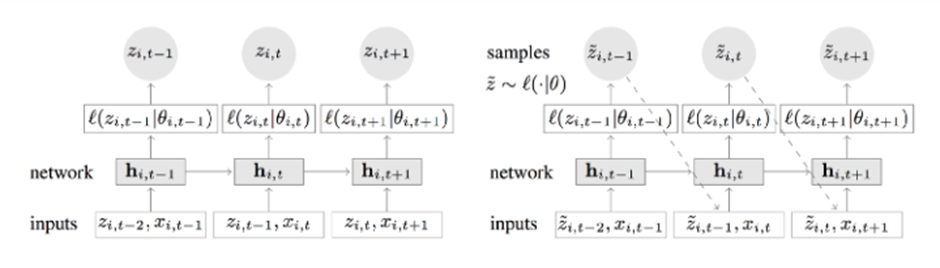
여기서 $h_{i,t}$ 는 각 time에 대한 RNN의 출력값이다

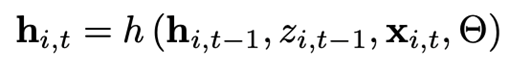
Large theta는 LSTM의 parameter를 의미한다

train
이 architecture 뒤에 있는 아이디어는 직관적이다:
여기서의 목표는 each time step의 분포에 대해 예측하는 것이다 이것은 network 가 이전의 관찰값( $z_{t-1}$ )을 optional covariates인 $x_i$ 와 함께 input으로 받아야 한다는 것을 의미한다.
( 그 시점의 관찰 값을 추정하는 것이기 때문이 한 타임 이전스텝의 값을 받는다)
그 정보는 hidden layer로 전파된다 여기서는 loss function대신 objective function으로 likelihood function을 사용한다 likelihood function은 Gaussian 이거나 Negative Binomial 일 수 있다

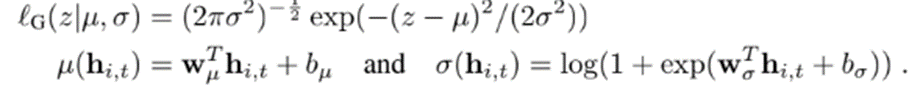
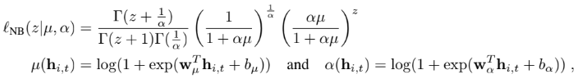
왜 데이터를 모델링 할 때 Negative Binomial Distribution을 사용했나?
Poisson Distribution은 우리가 어떤 단위시간 동안에 일어나는 사건의 평균횟수를 알고 있고 확률변수를 단위시간에 특정사건이 몇 번 발생을 할 것인지가 확률변수이다 따라서 이 논문에서 만약 주문을 100회 하는 경우를 모델링 하는 경우이면 Poisson Distribution을 사용해도 되지만 이경우엔 한번의 주문에서 여러 개의 제품을 주문하는 경우도 포함한다 이 경우 Poisson Distribution Family인 Negative Binomial Distribution을 사용하면 모델링이 잘된다는 결과가 다른 논문에 나와 있다

우리는 아래의 Objective Function의 stochastic gradient descenting을 통해 RNN의 h(·)에 구성된 가중치 𝛩뿐만 아니라 위의 θ(·)의 가중치 또한 갱신할 수 있다

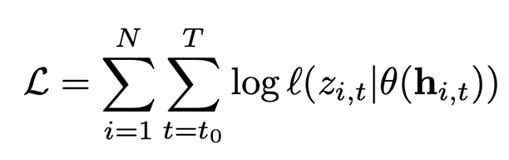
t = $t_o$ ~ $T$ : prediction의 모든값
i = $1$ ~ $N$ : 모든 Time Series

우리는 물건 데이터 집합의 각 시계열에 대해 원래 시계열과는 다른 시작점을 선택해서 여러 개의 Training Instance를 생성한다 이때 전체길이 T뿐만 아니라 모든 Training Instance에 대해 conditioning range의 길이와 prediction range의 길이를 같게 설정한다

예를 들어, 주어진 시계열의 총 사용 가능 범위가 2013-01-01부터 2017-01-01까지일 때 우리는 training example을 1일 단위로 생성해서 2013-01-01, 2013-01-02, 2013-01-03 이런 식으로 생성할 수 있다 이때 training window는 우리의 ground-truth-data를 prediction window가 포함하도록 생성해야한다

여기서는 Window Size = T만큼 random 하게 값을 추출해서 사용한다
(이를 추출해서 Train할 때 사용한다)

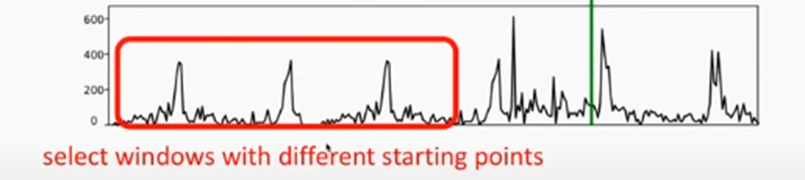
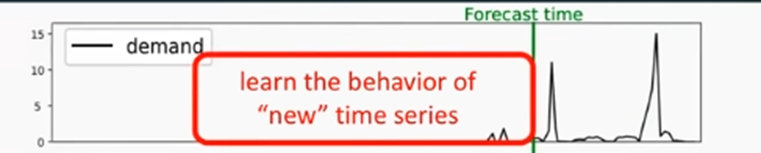
그러나 우리는 시계열 데이터 시작 전 값인 2012-12-01이 시작점으로 선택 할 수도 있다 이러한 관측되지 않은 target값은 0으로 채운다. 이러한 과정으로 인해 새롭게 나타나는 시계열의 행동에 대해 학습할 수 있도록 한다

"ground-truth"은 '우리가 정한 정답', '우리의 모델이 우리가 원하는 답으로 예측해주길 바라는 답'이다.

By augmenting the data using this windowing procedure, we ensure that information about absolute time is only available to the model through covariates, but not through the relative position of z_i,t in the time series

→ 시간에 대한 정보는 model의 covariates로 제공될 수 있고 상대적인 위치로는 제공 될 수 없다

prediction
우리는 encoding과정에서 마지막으로 얻은 cell state값을 prediction의 초기값으로 설정하고 encoding에서 얻은 마지막 output값을 prediction의 초기 관측 값으로 설정한다
이제 미래를 예측할 시간이다: 유념해야 할 것이 우리가 매 time step에서 얻는 예측은 distribution인 것을 기억해라 우리는 첫번째 timestep에서 output distribution으로부터 하나의 sampled를 뽑음으로써 시작한다 여기서 뽑은 sample은 두번째 time step에서의 input이 되고 and so on.
이렇게 만들어낸 Objective function을 Backpropagation을 통해 모델 파라미터 최적화를 진행한다

Scale handling

우리가 일상에서 쉽게 볼 수 있는 Power-law distribution을 보이는 data에 모델을 적용하는 것은 두가지의 문제점이 있다

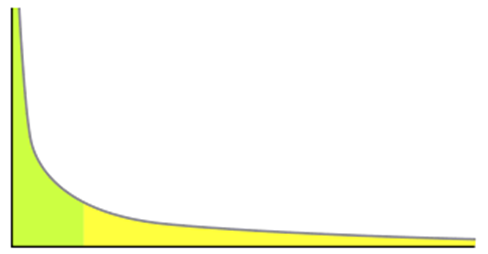
첫째로 모델의 autoregressive 속성 때문에 input과 output이 observation $z_{i,t}$ 의 scale에 직접적으로 영향을 받는다 따라서 이를 input layer에서 적절히 scale 해주고 output layer에서 다시 inverse 해주는 방법을 사용한다

여기서 그럼 $||z||$ 는 무엇이냐? 이는 item-dependent scale factor $v_i$ 로 scale을 하는데 예를 들어 negative binomial likelihood function에는 다음과 같이 scale 해준다

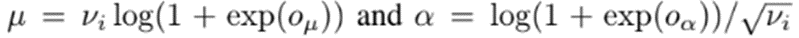
이 논문에서는 v_i를 heuristic하게 선택한 average value로 scale을 해봤는데 모델의 성능이 괜찮았다

두번째로 대부분의 상품이 적게 팔리고 아주 극소수의 상품만이 많이 팔리는 데이터의 불균형 때문에 training instance를 random하게 뽑아버리면 많이 팔리는 극소수의 상품이 뽑힐 확률이 매우 적고 결국 모델이 underfitting 될 가능성이 있다 이는 demand forecasting에서 많이 팔리는 상품을 더 잘 예측하는 것이 business 측면에서 유리하기 때문에 non uniform하게 데이터를 선택해야한다
(이 논문의 저자들은 Amazon에 소속돼있기 때문에 이러한 것들을 고민하는 것이다 실제로 DeepAR을 사용해보니 많은 종류의 데이터를 다룰 기회가 없다면 별 의미가 없는 단락이다)

ForeCasting

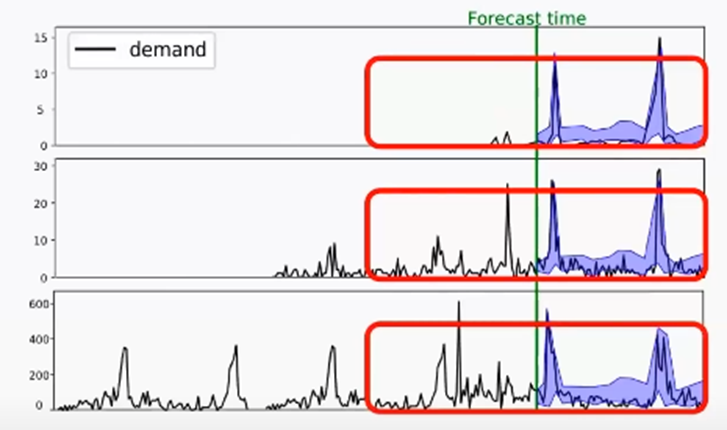
Monte Carlo방식으로 확률분포를 만들어 낸다
이때 하나의 선만을 보고 싶으면 Median 값을 사용하면 된다

Results

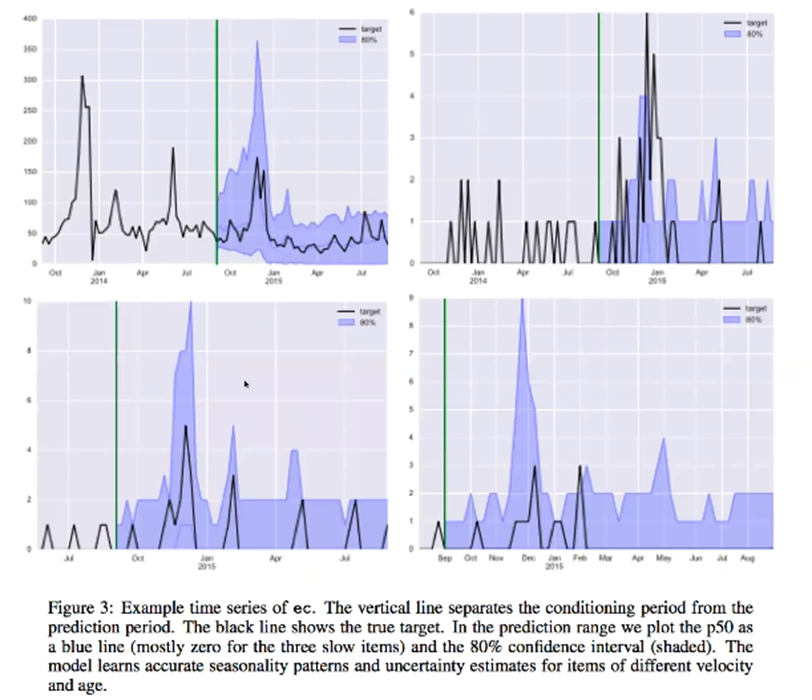
이 결과에서 중요한 것은 이전의 데이터가 거의 없고 거의 안 팔리는 것도 어느정도 잘 맞추는 걸 볼 수 있다

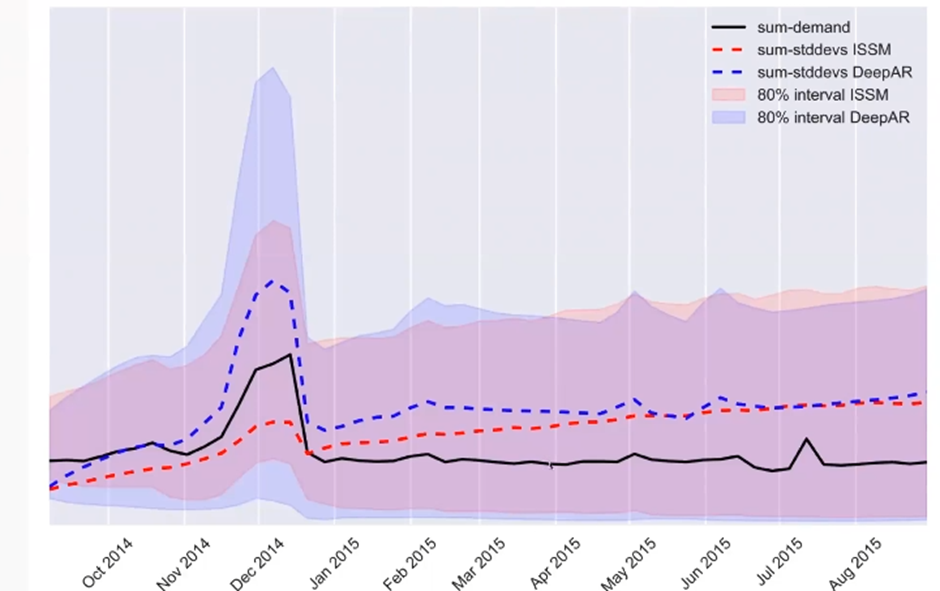
모델의 Forecasting Interval을 보면 미래로 갈수록 더 불확실한 것을 Interval의 크기가 커지는 것으로 보여주고 있다

Conclusion
Benefit of DeepAR model

다양한 관련된 시계열로부터 학습을 하는 Global 모델을 만들었다
Scale이 다양한 시계열들을 handling 했다
Generates calibrated probabilistic forecasts with high accuracy

Calibration(교정): Calibration은 딥러닝 에서 매우 중요하다
Calibration이란 모델의 출력값이 실제 Confidence를 반영하도록 만드는 것이다 예를 들어서 X에 대한 Y1의 모형의 정확도(accuracy) 출력이 0.8이 나왔을 때 이를 Confidence level로 보고 80퍼센트의 확률로 Y1일 것 이라는 의미이다 즉 Confidence level과 accuracy가 같게 만드는 것이다 https://3months.tistory.com/490
여기서 Calibrated Probabilistic Forecast라는 것은 높은 정확도에 대한 높은 신뢰도를 보장하는 예측을 생성한다고 해석할 수 있다

→ 한마디로 내예측이 신뢰 가능한 예측이라는 말이다

DeepAR은 계절성과 데이터의 Forecasting이 길어지는 것에 따른 불확실성의 증가 또한 가능하다

깃허브에 현실적으로 DeepAR을 사용했을때의 결과를 올려놓았으니 참고하길 바랍니다 !
https://github.com/leesungjoon-net

이성준

Time-Series

다음 포스트