오늘은 Transformer Paper Review와 덧붙여 관련 얘기를 해볼 것이다.
우선 Transformer는 자연어 처리에 더욱 적합하게 탄생한 모델인 것 같다는 내 생각을 밝히면서 시작하겠다 논문에 Introduction에서 언어모델과 관련된 얘기를 하는 것으로 보아서 저자들도 애초에 자연어 처리를 염두해두고 논문을 썼다고 생각한다. 그렇다면 왜 Forecasting을 공부하면서 Transformer를 공부하냐? 최근에 나오는 논문들은 Transformer기반의 Long Time Series Forecasting을 하는 Model들이 많이 나왔기 때문이다 기본적으로 자연어 처리도 Sequence Data를 사용하니까 견문을 넓히기 위해 Transformer는 꼭 공부하고 넘어가야한다.
오늘의 개요를 먼저 알리겠다.
- Seq2Seq Model(Encoder-Decoder 모델)
- Attention
2.1. Attention의 Idea
2.2. Attention Function
2.3. Dot-Product Attention - PaperReview
1.Seq2Seq Model(Encoder-Decoder 모델)
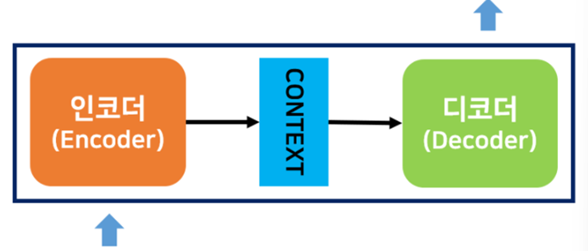
Encoder는 입력 데이터를 인코딩하고, Decoder는 인코딩된 데이터를 디코딩하는 역할을 맡는다.
즉, 시계열 데이터에서는 어떤 시게열 데이터를 압축해서 표현해주고 Decoder는 압축된 데이터를 다른 시계열 데이터로 변환해 준다.
우리는 RNN이나 LSTM을 사용해서 Seq2Seq를 구성할 수 있는데
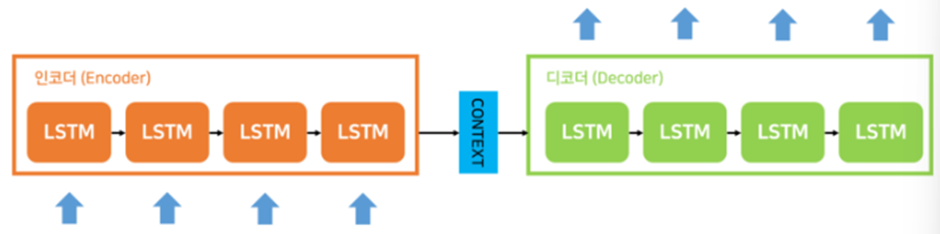
인코더의 출력으로 나오는 Context가 바로 Context Vector(문맥벡터)이고 마지막 hidden state이다 따라서 이는 고정 길이 벡터이다
그래서 결국 인코더에서의 Process는 시계열 데이터를 고정길이 벡터로 변환하는 작업이 된다
Decoder의 구조는 다음과 같다
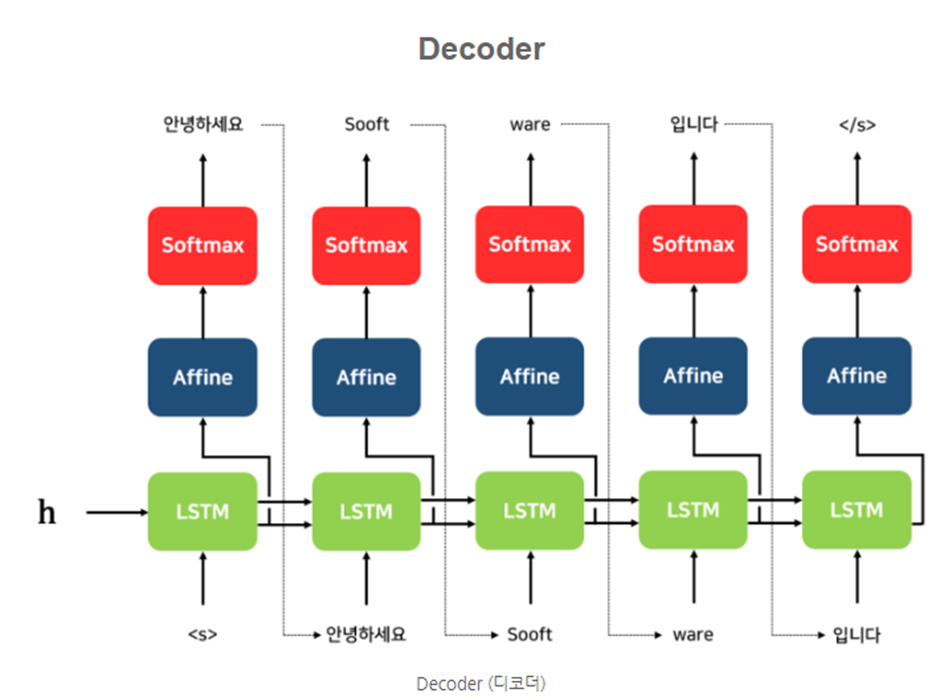
여기서 처음에 들어가는 s는 Start of Sequence를 의미한다
Affine 계층은 Hidden State를 입력으로 받아 분류 개수로 출력해주는 FeedForward 네트워크이다
위처럼 하나의 Context Vector로 압축해서 Decoding을 하는 방식은 2가지의 문제가 있다
- 하나의 고정된 크기의 벡터에 모든 정보를 압축하고자 하니깐 정보 손실이 발생한다
- RNN(LSTM)의 고질적인 문제인 Gradient Vanishing문제가 존재한다
결론적으로 Sequence가 긴 데이터에 대해서는 병목현상(Bottle Neck: 담을 수 있는 데이터의 양은 적으나 한꺼번에 많은 양의 데이터가 유입됨으로써 컴퓨터가 느려지는 현상)이 나타났고 이런 병목현상을 해결하기 위해서 Attention 기법이 나오게 됐다
2. Attention
2.1. Attention의 Idea
Attention의 기본 아이디어는 Decoder에서 출력 단어를 예측하는 매 시점(step)마다, 인코더의 입력 시퀀스를 다시 참고하는 것이다
이때 입력 시퀀스를 동일한 비중으로 참고하는 것이 아닌 예측단어와 관련이 있는 입력단어를 더욱 치중(Attention)해서 보기 때문에 Attention이라는 단어를 사용한다
우리 TimeSeriesForecasting을 할때는 여기서 예측단어가 아닌 예측 시점에서의 데이터 집합이라고 생각하면 된다
2.2. Attention Function
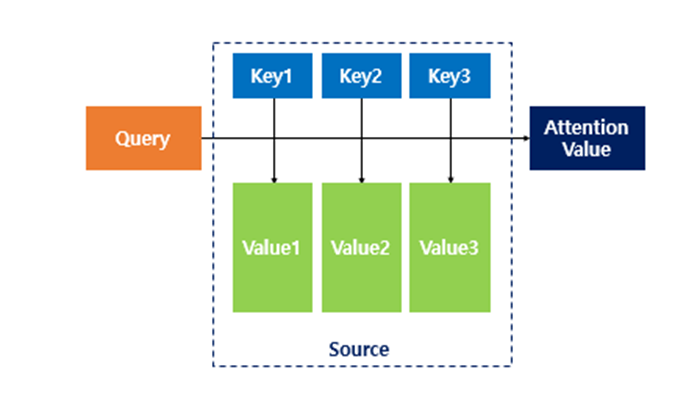
Attention Function은 주어진 Query에 대해 모든 key의 유사도(Attention Score)를 각각 구한다.(Vector Similarlity라고 생각) 그리고 이 유사도(Score)를 Key와 Mapping된 각각의 Value에 반영해준다. 그리고 유사도가 반영된 값을 모두 더한 Attention Value를 반환한다.
2.3. Dot-Product Attention
Seq2Seq에 Attention 기법을 적용한 예시의 기본 형태인 Dot-Product Attention이다
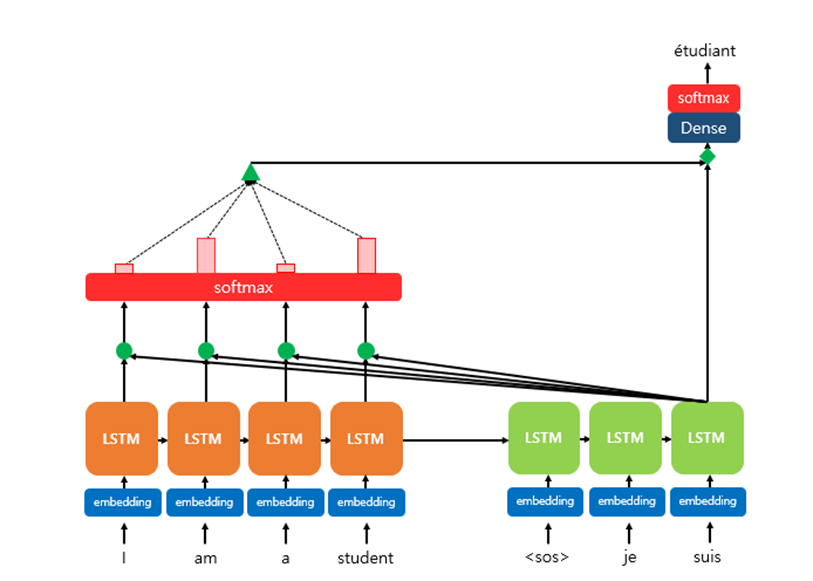
위 그림은 Decoder의 세번째 LSTM Cell에서 출력 단어를 예측할 때 어텐션 메커니즘을 사용하는 예시이다
여기서 Query, Key, Value는 다음과 같다

위 그림은 다음과 같은 Mechanism을 갖는다
-
Attention 매커니즘을 사용하기 때문에 Encoder의 Hidden State값을 Key, Value값으로 참고한다.
마지막 LSTM을 돌아서 나온 예측 Output과 Encoder의 모든Sequence(‘I’, ’am’, ’a’, ’student’)의 관계를 파악하게 된다(초록색 원에서 dot-product+Softmax를 진행함으로써 Attention Score를 계산) -
Attention Score(key와 곱연산)을 LSTM의 Output(Value)과 같이 고려해서 다음 예측을 낸다
여기서 Attention Value는 인코더의 맥락을 포함하고 있기 때문에 Context Vector라고 부르기도 한다(정확히는, Decoder 내 특정 Time Step t의 Context Vector) -
Attention Value(a_t)와 decoder의 t시점의 hidden state(s_t)를 연결(concatenate)한다
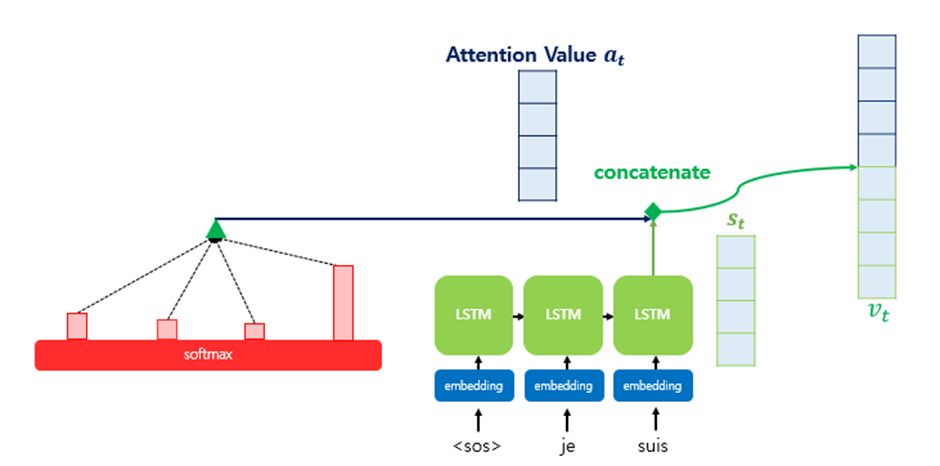
이렇게 Concatenate해서 얻은 V_t는 기존의 Recurrent하게 얻은 Decoder의 Hidden State 정보 와 Encoder에서 얻은 모든 Hidden State를 고려한 정보 또한 포함하고 있기 때문에, Sequence가 길어지더라도 정보를 크게 잃지 않는다 -
출력층 연산의 input이 되는 S(tilda)_t를 계산한다
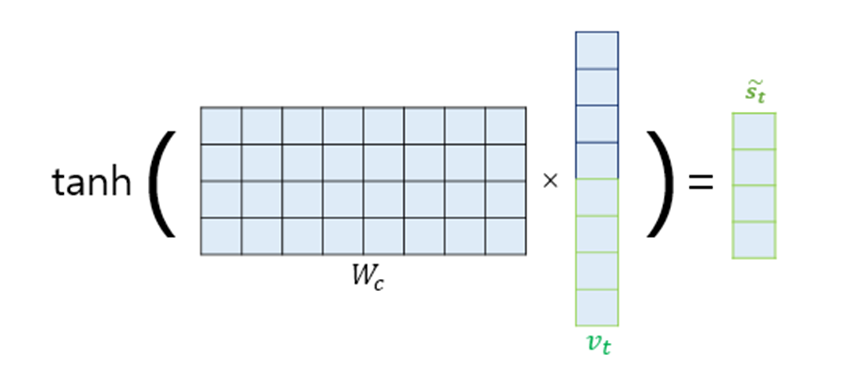
여기서 W_c는 학습가능한 가중치 행렬이다 -
Softmax를 통해 최종적인 예측을 얻는다
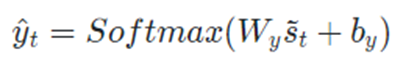
3. Paper Reveiw
Abstract와 Instroduction Background의 주요 내용은 RNN기반의 모델은 병렬처리를 제한하고 전역의존성을 이끌어내기 어려운데 (Gradient Vanishing에의해 ) Transformer를 사용하면 이런 문제를 해결할 수 있다는 정도만 알고 넘어가면 될 것 같다.
따라서 Model Architecture에 대한 이야기만을 하겠다.
3.1. Model Architecture
중요한 부분을 번역을 하되 내용에 대한 설명은
각 Part마다 밑에 따로 적어두겠다
3.1.1. Encoder and Decoder Stacks
Encoder: Encoder는 6개의 동일한 Layer의 Stack으로 구성 돼 있다 각각의 Layer는 2개의 Sub-layer들을 갖는다 하나는 Multi-head Self-Attention Mechanism을 갖고 두번째는 Position-Wise Fully Connected Feed-Forward Network를 갖는다.
우리는 Residual Connection을 layer normalization과 함께 두개의 Sub layer에 사용한다.
LayerNorm(x+Sublayer(x))
이런 Residual Connection이 가능케 하기 위해서 우리는 Encoder에 모든 요소에서 같은 차원(512차원)의 Output들을 만들어낸다.
Decoder: Decoder 또한 Encoder와 같은 수의 동일한 Layer들로 구성돼 있다. Decoder Layer는 세번째 Third Layer를 추가했는데 이는 Encoder의 Output에 대해 multi-head Attention을 수행한다.
Encoder와 마찬가지로 각각의 Sublayer에 Residual Connection과 Layer Normalization을 수행한다
우리는 Decoder에서 Self-Attention Sub-Layer를 Subsequent Positions의 참여로부터 Positions를 보호하기 위해 수정했다. 이를 Masking이라고 한다.
이는 position i에 대한 예측을 수행할 때 우리는 오롯이 i 이하의 positions에 대한 알려진 output값에만 의존한다.
보충설명
ADD&NORM LAYER
우리는 Embedding된 Word에 positional encoding을 더해 줬었는데 딥러닝 학습을 하다 보면 역전파에 의해서 이 Positional Encoding이 손실될 수 있다 이를 보완하기 위해서 Residual Connection으로 입력 값을 다시 한번 더해주는데 이과정이 Add 과정이다
Residual Connection: 일부 레이어를 건너뛰어 데이터가 신경망 구조의 후반부에 도달하는 또 다른 경로를 제공함으로써 Gradient가 계속 커지거나 작아지는 문제를 해결한다
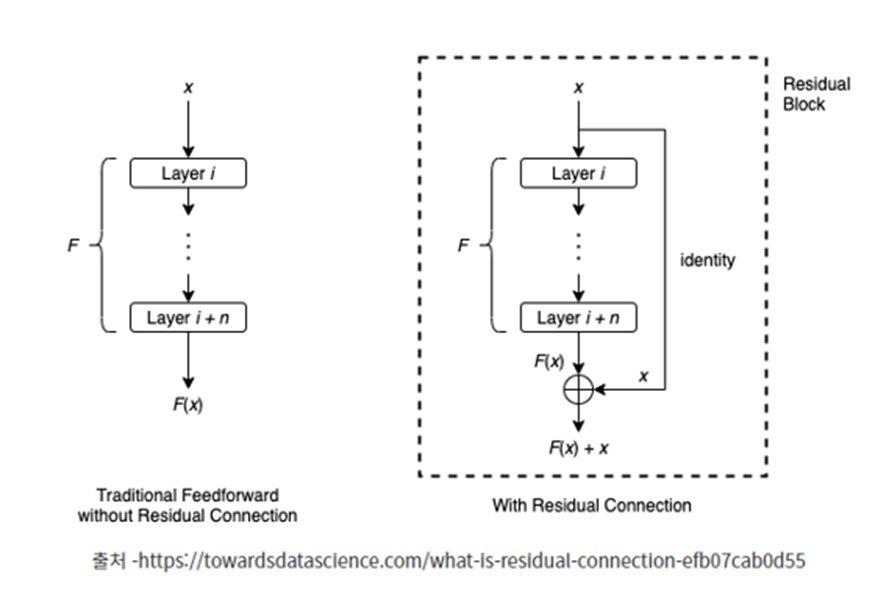
즉, 레이어 i를 통과하기 전 입력값 x를 그대로 들고 와 최종 output에 더해주는 F(x)+x의 형태가 되는 것이다. 입력 x를 취해서 출력 F(x)+x를 생성하는 전체구조를 보통 Residual block이라고 한다 수백 개의 레이어가 있어도 Residual block이 포함된 신경망은 경험적으로 훨씬 더 용이하게 수렴하는 것을 나타내고 있다
Layer Normalization:
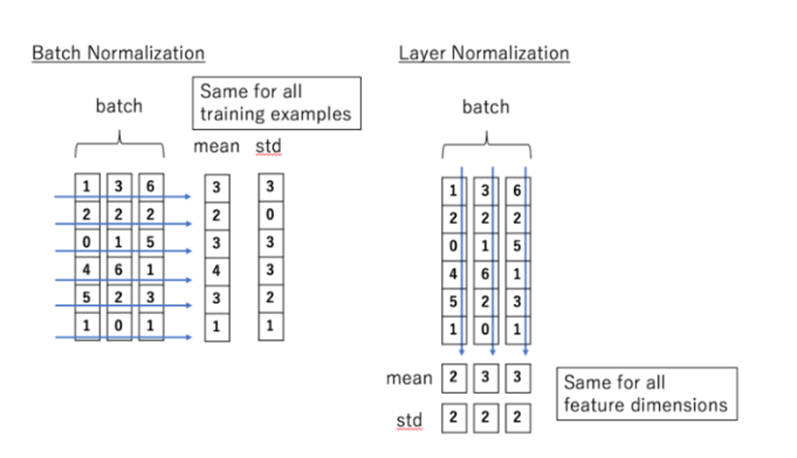
Batch Normalization은 특징별로 평균과 분산을 계산해야 한다
Layer Normalization은 데이터별로 정규화 한다 그러므로 데이터별로 평균과 분산을 계산해서 정규화 과정을 거쳐야한다
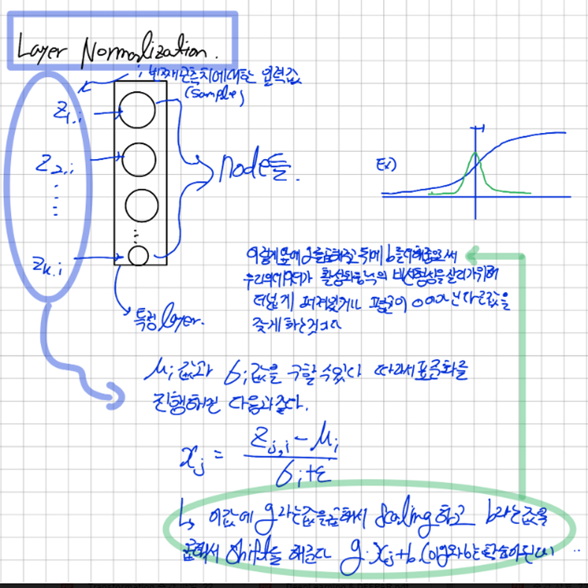
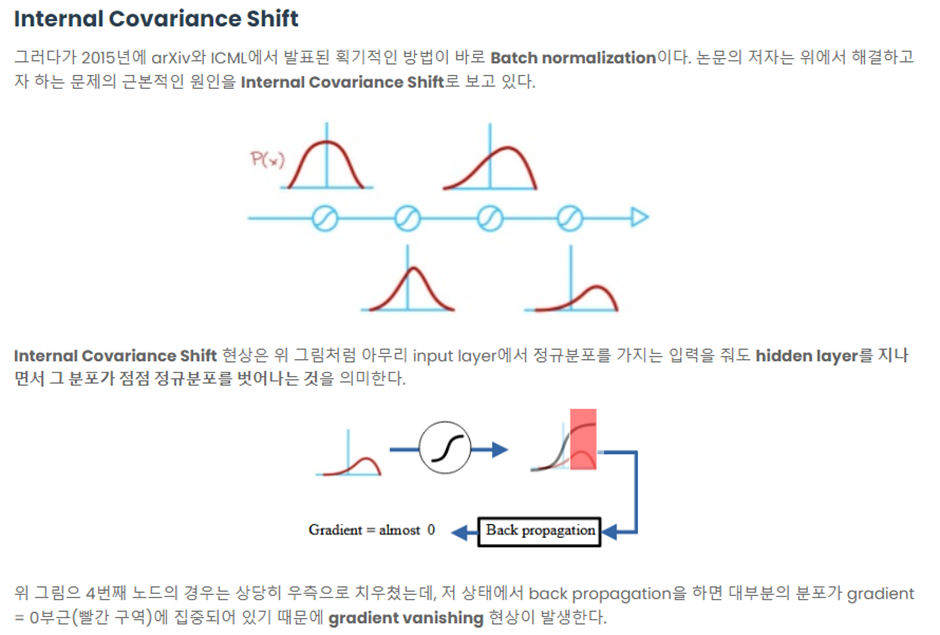
https://sonsnotation.blogspot.com/2020/11/8-normalization.html
3.1.2 Attention
Attention function은 Query와 Output에 대한 Key-Value쌍의 set를 Mapping하는 것으로 표현될 수 있다 Output은 Value들의 가중합으로 계산된다 weight는 각각의 Value의 할당되고 이는 각각의 Query와 상응하는 Key의 Compatibility Function에 의해 계산된다
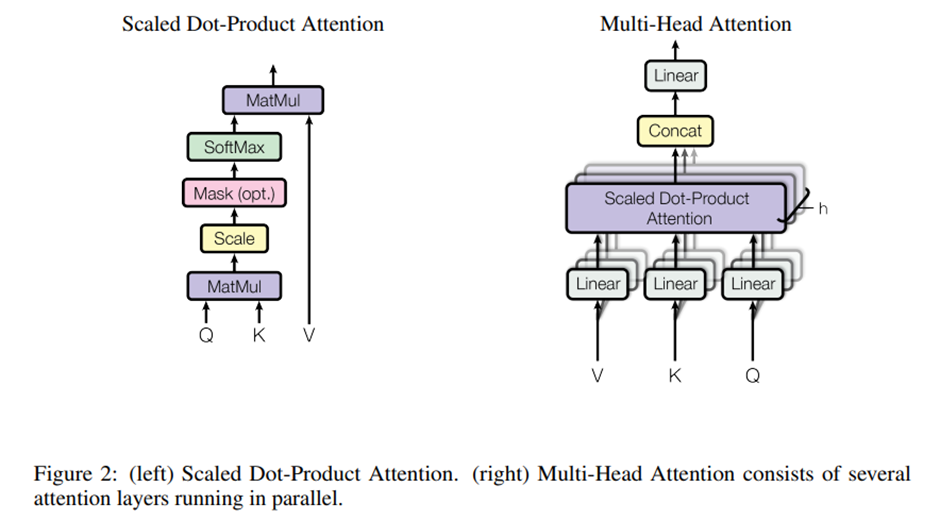
Scaled Dot-Product Attention:
우리는 각각의 Attention을 Scaled Dot-Product Attention이라고 부른다.
Input은 차원의 Query들과 Key들 그리고 차원의 Value들로 구성돼 있다 우리는 모든Query들과 Key들을 Dot product를 계산하고 이를 로 나눠준다 그후 Softmax function을 적용해 Value에 대한 Weight(Attention Score)를 얻는다
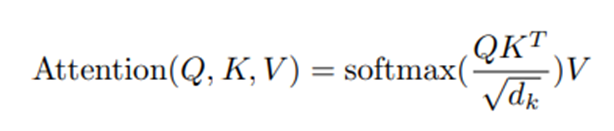
가장 흔하게 쓰이는 Attention function들은 Additive Attention, Multiplicative[dot product] Attention이 있다
보충설명
Query, Key, Value와 Scaled Dot-Product Attention(≈ Self Attention )
인풋 벡터가 들어오면 Self-Attention층에서는 쿼리(Q),키(K),밸류(V) 벡터를 인풋 벡터의 수만큼 준비한다
쿼리: 현재 처리하고자 하는 토큰을 나타내는 벡터
키: 일종의 레이블(label)로, 시퀀스 내에 있는 모든 토큰에 대한 identity를 나타낸다
밸류: 키와 연결된 실제 토큰을 나타내는 벡터
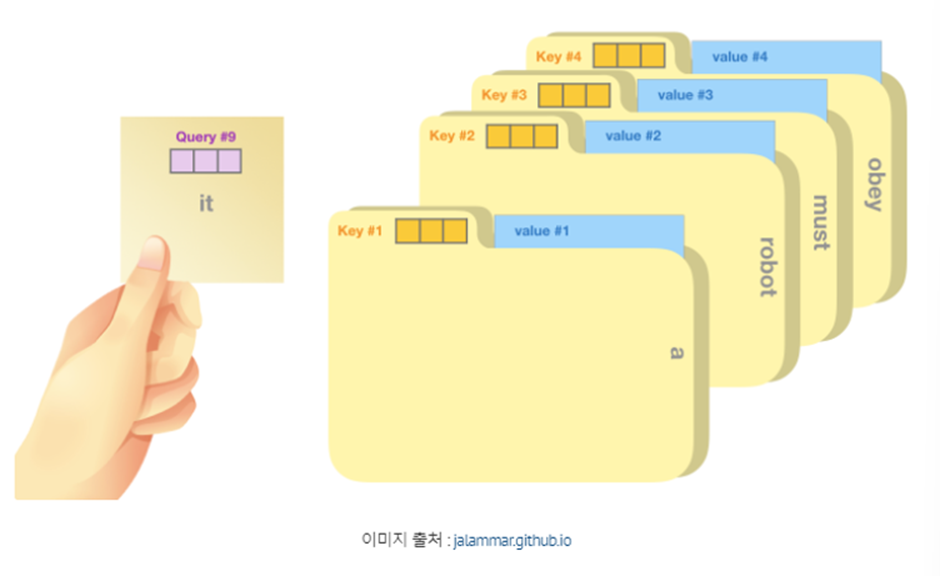
Encoder의 제일 아래의 Sub layer에서 이뤄지는 연산과 Decoder의 제일 아래의 Sub layer에서 이뤄지는 Attention연산을 SELF ATTENTION이라고 한다 물론 Decoder의 제일 아래의 Sub layer에서 이뤄지는 연산은 학습과정에서 미래의 값을 가릴 필요가 있기 때문에 Masking 돼있다

Self-Attention에서는 Query, Key, Value를 위와 같이 정의할 수 있다
입력벡터라고 표현했지만 실제로는 학습이 가능한 행렬 ,,를 곱하여 Query, Key, Value를 얻는다
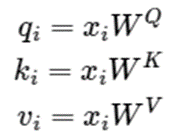
이때 , 는 ( x ) 는( x )
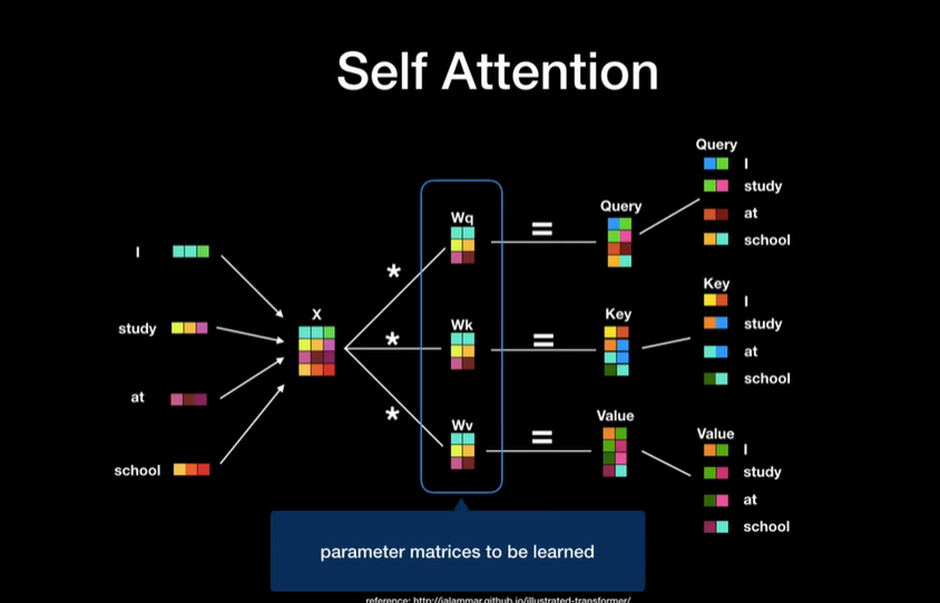
여기에 Query, Key, Value는 각각 , , 의 행렬에 의해서 생성이 되고 행렬들은 단순히 Weight Matrix로 딥러닝 모델 학습 과정에서 최적화가 일어난다
Word Embeding은 Vector이고 실제 문장은 행렬이라고 할 수 있다
Query, Key, Value는 벡터의 형태이다
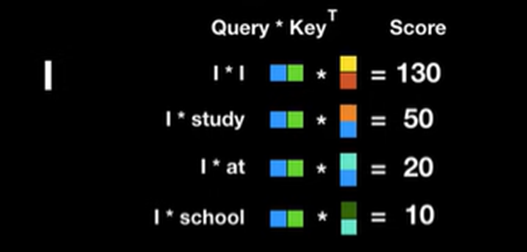
여기서 Query와 Key Transpose를 곱하면 이를 Attention Score라고 하고 이는 단어와 단어가 연관이 있는 정도이다
어떻게 Query와 Key를 곱했을 때 높은 연관도를 가진 벡터들의 Score값은 높게 나오고
낮은 연관도를 가진 벡터들의 Score값은 낮게 나오나?
Self-Answer
→ 벡터들의 내적을 생각해보면 된다 백터들의 크기가 다 비슷하다고 가정하면 한 벡터와 내적 했을 때 가장 큰 값이 나오는 값은 자기 자신과의 곱일 것 이다(구 안에 한 벡터)

Sqrt(dimension of key)로 나눠준 이유는
Key vector의 차원이 늘어날수록 Dot product 계산 시 값이 증대되는 문제를 해결하기 위해 나눠줬다
→여기서 Sqrt로 나눠주는 과정이 Scale하는 과정이라고 해서 Scaled dot-product Attention이라고 불린다
→Attention(Q,K,V) = Softmax( – Scaled dot-product attention
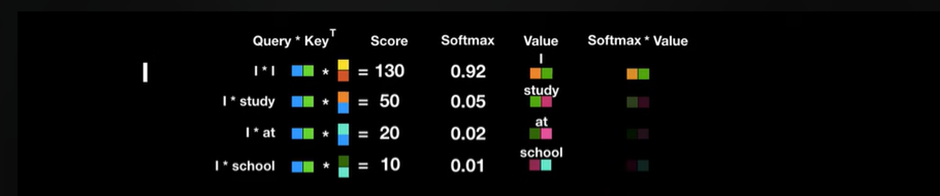
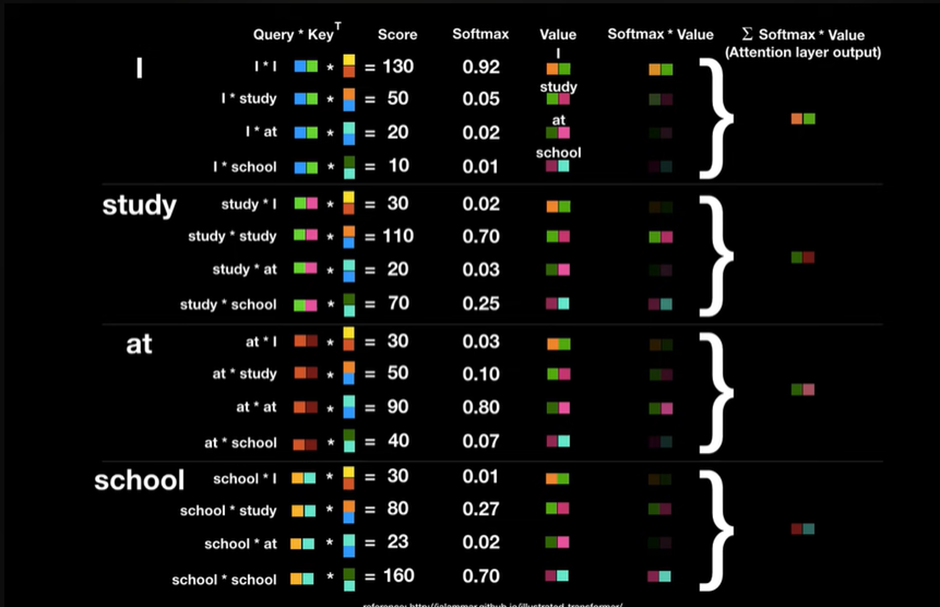
Softmax로 나온값은 Key 값에 해당하는 단어가 현재 단어의 어느정도 연관성이 있는지 나타낸다
예를 들어 단어 I는 자기 자신과 92프로 Study와 5프로 ,,,
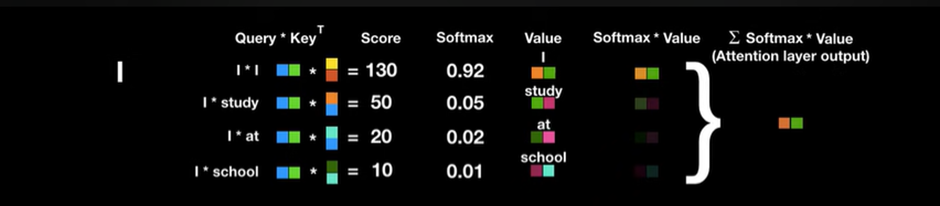
최종으로 다 더한 벡터는 단순히 단어I가 아닌 문장속에서 단어 I가 지닌 전체적인 의미를 지닌 벡터라고 간주한다
3.1.3. Multi-Head Attention
(=512)차원을 가지는 Keys, Values, Queries를 single head attention function에서 수행하는 것 대신에
우리는 Queries, Keys, Values 각각 h번 서로 다른 그리고 학습된 linear projection으로 {}와{} 차원에 linear하게 Project하는게 더 효과적이라는 사실을 알아냈다
이 project된 queries, keys, values를 우리는 attention function에 넣어서 병렬적으로 수행하고 {} 차원의 output value를 만들어낸다
이 결과들을 concatenate 시킨 다음 다시 한번 project(와의 내적) 시켜서 최종 결과값을 만들어 낸다
(여기서 다른 차원으로 Project 시킨다는 말은 그 크기에 맞는 가중치 행렬을 곱한다는 뜻이다)
Multi-head attention은 모델이 서로 다른 가중치 초기값을 갖게 해서 다양한 결과값을 내게 하는 점에서 의미가 있다

이 연구에서는 h=8이고 = 64
→각 head마다 차원을 줄여주기 때문에, 전체 계산 비용은 전체 차원에 대한 Single-head attention과 비슷하다
보충설명
Multi-head Attention의 필요성과 과정
Multi-head attention은 여러 관점에서 하나의 데이터를 들여다보겠다는 것이다 그리고 각각의 관점에서 Concatenate를 시켜서 이후의 과정을 해보겠다는 것이다
예를 들어 “그 동물은 길을 건너지 않았다. 왜냐하면 그것은 너무 피곤하였기 때문이다” 라는 문장을 생각해보자
‘그것’이 쿼리벡터라고 하면 다른 단어와의 연관도를 구했을 때 첫번째 Attention head는 ‘그것’과 ‘동물’의 연관도를 높게 본다면, 두 번째 어텐션 헤드는 ‘그것’과 ‘피곤하였기 때문이다’의 연관도를 더 높게 볼 수 있다
→ 자칫하면 자기 자신과의 연관도 만을 높게 평가하는 것과는 달리 여러 의견을 들어봄
이는 각 어텐션 헤드는 전부 다른 시각에서 보고 있기 때문이다
즉, 사람의 문장은 모호할 때가 상당히 많고 한 개의 Attention으로 이 모호한 점을 충분히 Encoding하기 어렵기 때문에 Multi Head Attention을 사용해서 되도록 연관된 정보를 다른 관점에서 수집해서 이 점을 보완할 수 있는 것이다
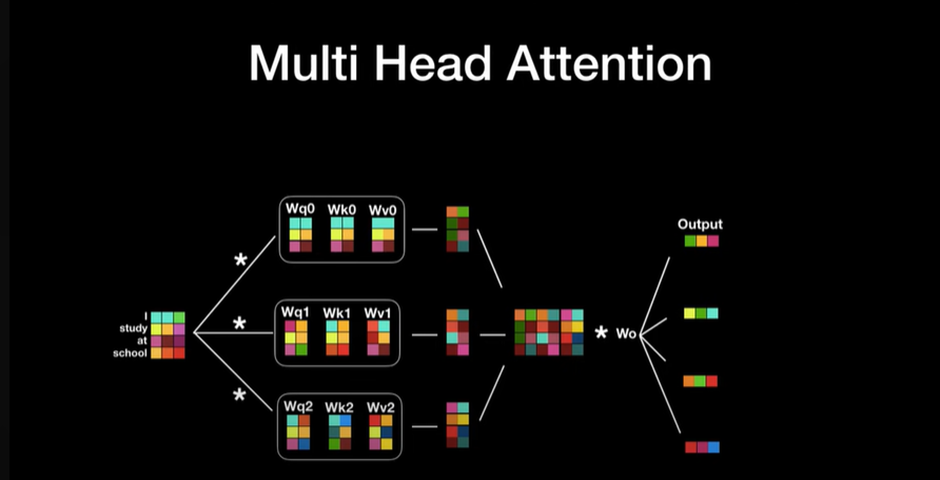
여기서 Wq0,Wq1,Wq2는 서로 다른 행렬(크기는 같음 논문에서는 512x64)이고 Wk0,Wk1,Wk2 와 Wv0,Wv1,Wv2 또한 마찬가지이다
이때 처음의 input의 size가 (input_length x d_model) 이었다면 하나의 head에서 나오는 output 의크기 이기 때문에 이의 크기는 input_length x d_v이고 이런 head가 h개 있고 열을 기준으로(axis=1)concat하므로 사이즈가 input_length x h*d_v가 되고 output matrix를 곱하면 처음의 input_size인 (input_length x d_model)가 나오게 된다.
3.1.4 Applications of Attention in our Model
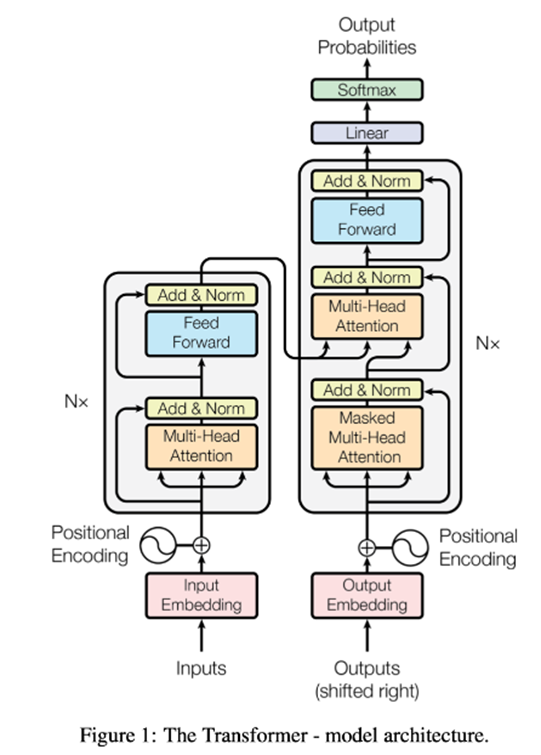
Transformer는 세가지 방법으로 Multi-head Attention을 사용한다
1. 인코더-디코더 Attention layers에서 (Decoder Part)
- Query 는 이전 디코더 layer에서 나온다
- memory key와 value는 인코더의 output에서 나온다
- 따라서 디코더의 모든 position이 input sequence의 모든 position을 다룬다
- 전형적인 Seq2seq model에서의 인코더-디코더 Attention 방식이다
(디코더의 hidden state가 인코더의 Key-value 를 고려)
- Encoder의 Self-attention Layer를 포함하고 있다(Encoder Part)
- Self-attention layer에서 key,value,query는 모두 같은 곳(인코더의 이전 layer의 output)에서 나온다
- 인코더의 각 position은 인코더의 이전 layer의 모든 position을 다룰 수 있다
- Decoder 또한 Self-Attention Layer를 갖는다(Decoder Part)
- 마찬가지로, 디코더의 각 position은 해당 position까지 모든 position을 다룰 수 있다
- 디코더의 leftforward information flow는 auto-regressive property때문에 막아줘야 할 필요가 있다
- 우리는 이를 Scaled dot-product attention 안에서 illegal connection에 해당하는 softmax의 input value들을 – inf로 masking 해서 구현한다
3.1.5 Position-wise Feed-Forward Networks
우리의 Encoder와 Decoder Layer 각각에는 Fully Connected Feed-Forward Network가 있다 이는 두가지의 ReLu 활성화 함수를 포함한 Linear Transformation으로 구성된다
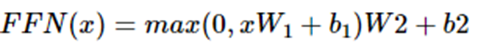
Linear transformation은 different position에 대해서는 동일하지만 layer간에 parameter는 다르다
3.1.6 Embeddings and Softmax
(a)다른 Sequence Transduction models 처럼, 학습된 임베딩을 사용한다
이는 input 토큰과 output 토큰을 d_model 차원의 벡터로 변환하기 위함이다
(b) decoder output을 출력한다음 다음에 올거라고 예측된 토큰의 확률로 변환하기 위해서 선형 변환과 Softmax를 사용했다
(선형변환을 통해 모델이 갖고 있는 언어 벡터 마다의 out vector의 Score를 계산하고 이를 softmax로 확률 계산을 한다)
Transformer에서는 두 개의 임베딩 Layer와 pre-softmax 선형 변환 간, 같은 weight matrix를 공유 한다
3.1.7 Positional Encoding
우리의 모델은 RNN이나 CNN기반이 아니기 때문에, 모델이 Sequence의 순서(어순)을 사용하기 위해서는 우리는 Sequence안에 있는 토큰의 상대적이고 절대적인 위치에 대한 정보를 주입해야한다
우리는 encoder,decoder stack의 처음에 Positional Encoding이라는 d_model dimension을 가진 벡터를 더한다
이 논문에서 우리는 다른 주기를 갖는 Sine과 Cosine함수를 사용한다
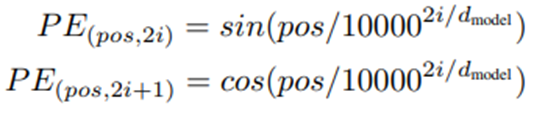
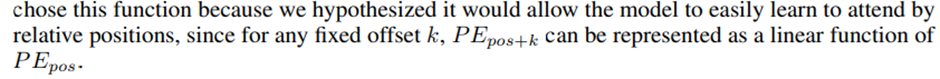
우리는 학습된 Positional Embedding을 사용해 실험을 해봤는데 여기서 사용하는 Positional Encoding방식과 Embedding방식은 거의 같은 결과를 보였다
Transformer에선 Sine 곡선의 방식을 택한다
-> 모델이 더 긴 Sequence의 길이를 추론할 수 있게 해주기 때문이다
3.1.8 Why Self-Attention
굉장히 빠르다는 걸 big-O notation을 사용해서 설명
보충설명
Encoder와 Decoder의 과정 및 모델설명
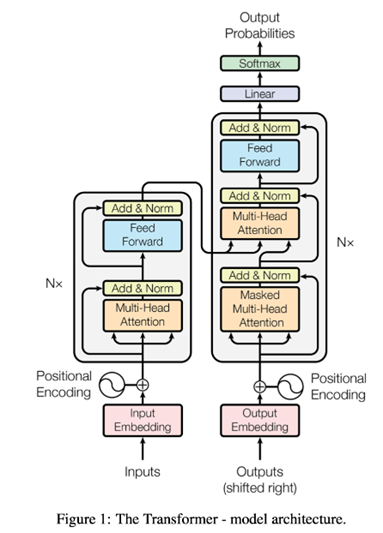
- Encoder Part
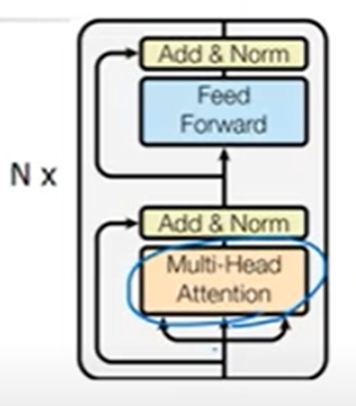
위의 그림이 Encoder Block인데 이게 6개를 거쳐서 나온다.
Encoder block을 여러개 쌓아서 만드는 이유는 Neural network를 깊게 만드는 것과 비슷한 느낌으로 받아들이면 된다.
Process
-
우리는 Input 문장을 받고 이 Input 문장에 대해 Embedding과정 즉, 각 단어를 벡터화 해주는 과정을 거친다
-
우리는 이렇게 바꾼 단어 벡터들에 대해 어순을 부여해주는 과정을 거치는데 이는 RNN과 LSTM을 사용한 모델의 경우 자동적으로 매 Step 마다 입력 값이 들어가 자동으로 어순이 들어 가는 것에 비해 Transformer의 경우 RNN,LSTM base가 아니기 때문에 어순을 Positional Encoding을 통해서 부여해 줘야 한다
그렇다면 어떻게 Position을 부여해 줄 수 있을까 이 Position은 아무렇게나 부여해서는 안되고 일정한 규칙을 거쳐야 한다
첫째, 모든 Position값은 시퀀스의 길이나 Input에 관계 없이 동일한 식별자를 가져야 한다 즉 Position값에 Depend 되는 값은 오롯이 위치만 Depend 해야 된다는 것이다.
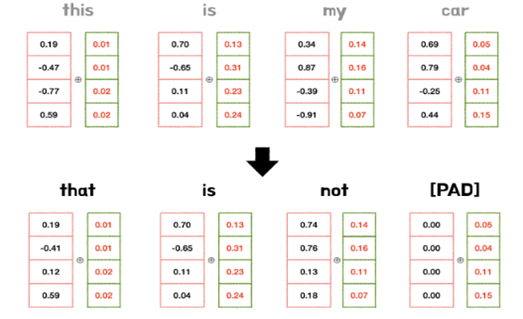
둘째, 모든 위치 값은 너무 크면 안된다. 위치 값이 너무 커져버리면, 단어와의 의미보다 위치 값에만 집중하는 경향이 생겨버린다
우리는 위 두가지 조건을 만족하는 Positional Encoding을 수행 해주는 Function을 Sine, Cosine함수를 각 벡터의 차원과 몇 번째 벡터인지를 고려해서 정의 했다
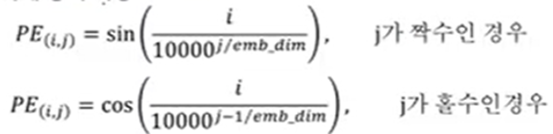
여기서 PE_(i , j)는 단어 i의 Positional Embedding Vector의 위치 j의 원소 값을 의미한다.
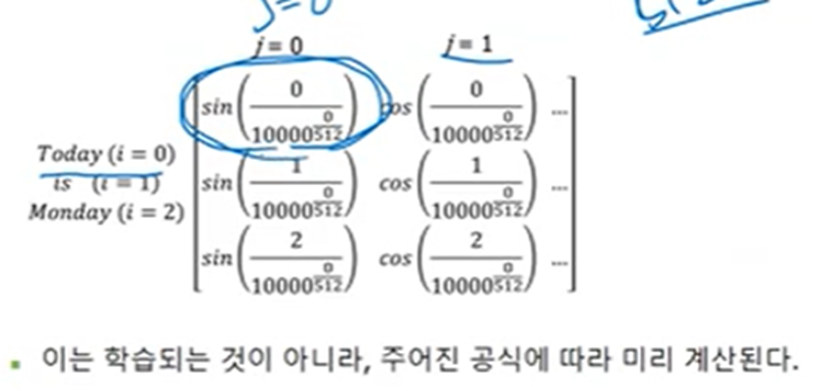
이렇게 구해진 위치정보를 원래 단어 벡터에 더해서 Encoding block안에 집어 넣는다 -
이후 이렇게 임베딩 된 벡터들을 행렬의 형태로 Multi-head Attention Layer에 집어 넣는다
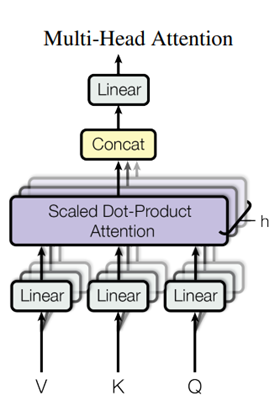
Input 행렬(단어 벡터들의 집합)을 입력 받고
위 그림의 Linear 파트에서 논문에서는 8개의 head로 나뉘어 각각의 Query와 Key, Value를 만들어 줬고 이것이 각각의 Scaled Dot-Product Attention을 거친 후 Concatenation된 이후 Linear 부분에서 다시 Input 행렬의 크기로 바꿔준다.(를 곱해주는 부분) -
이후 이를 위에서 설명한 Add & Norm 과정을 거치고 Feed Forward Layer로 올라간다
-
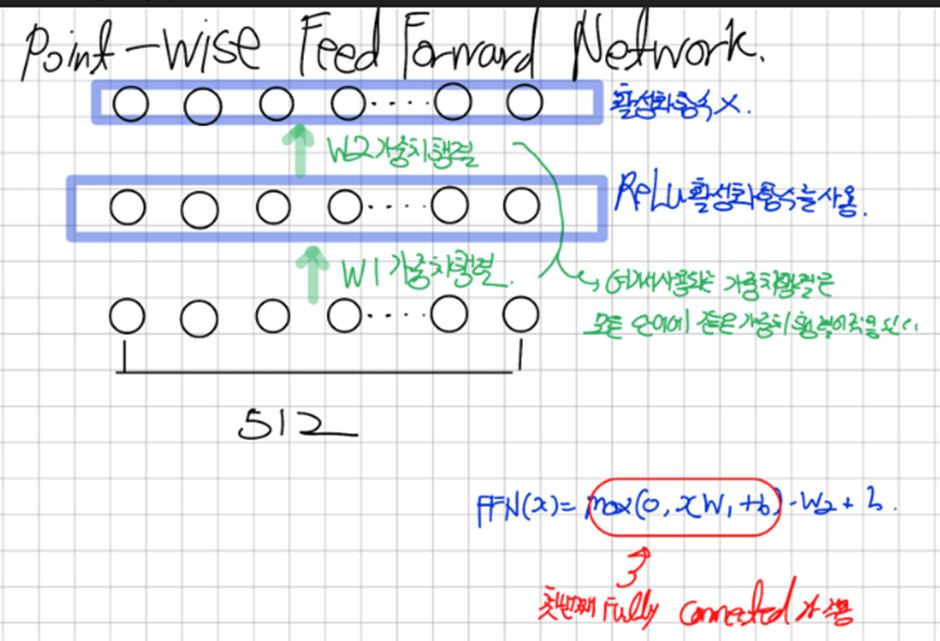
Position-Wise Feed Forward Network
여기서 말하는 Feed Forward Network가 바로 Position-Wise Feed Forward Network이다
Position-Wise Feed Forward Network;
Position(각각의 토큰 즉, 각각의 단어) 별로 서로 다른 두가지의 Feed-Forward Layer가 적용 된다는 의미이다
다시 말하자면 인코더 부분에 입력된 각각의 단어에 대해 두가지 종류의 Feed Forward layer에 입력이 됐다는 것을 의미한다
-
다시 Add& Norm 과정을 거친다
- Decoder Part
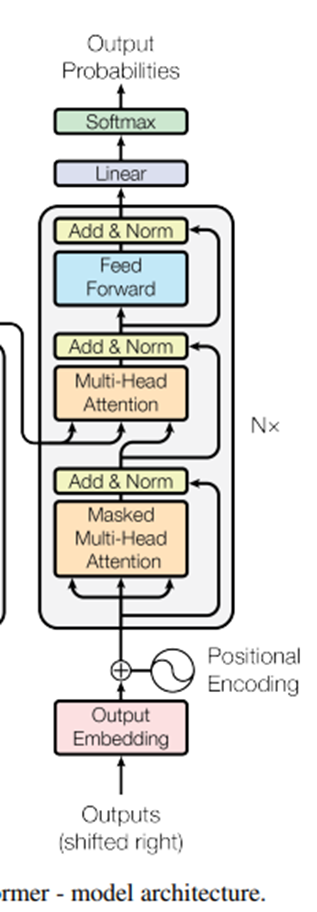
위 그림은 Decoder Block의 그림을 나타낸다 Decoder Block 또한 Encoder와 마찬가지로 6개의 Block이 연결된 형태를 갖고 있다
Decoder Part에서는 두가지 Attention을 사용하고 있는데
제일 아래에 있는 Masked Multi-Head Attention은 Self Attention으로써 Query, Key, Value가 전부 같은 행렬이 출처이고
다음에 있는 Multi-Head Attention은 Encoder의 출력행렬에 , 를 곱해서 Key와 Value를 Encoder에서 입력 받고 Query는 Sub layer의 출력 행렬을 이용한다 따라서 이를
Encoder-Decoder Attention라고 부른다
다른 그림으로 표현하면 다음과 같다
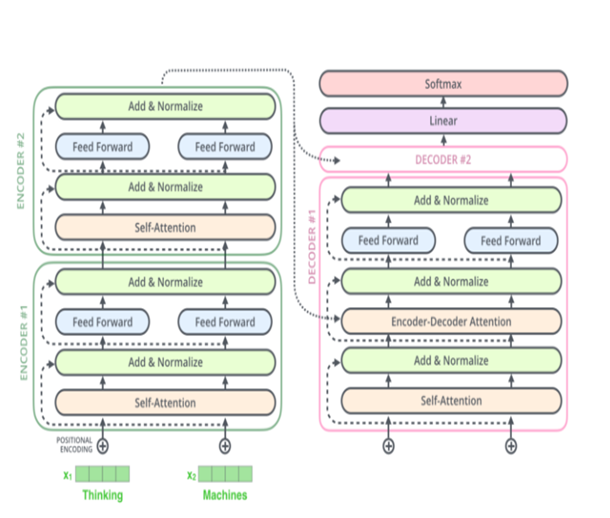
위에서 언급한 Attention들을 하나씩 알아보겠다.
Masked Multi-Head Attention을 이해하기 위해서는 먼저 학습(Training)과 실제로 구동하는 추론(Inference)과정에서 Decoder가 어떤 과정으로 학습하고 추론하는지 이해해야 한다
Transformer의 학습과정
Transformer의 학습 목표는 입력과 타겟 시퀀스를 모두 이용해서 타겟 시퀀스를 출력하는 방법을 학습하는 것이다
Transformer가 영어(입력 시퀀스)를 스페인어(타겟 시퀀스)로 번역하는 사례를 통해 Transformer의 학습하는 과정을 살펴보자
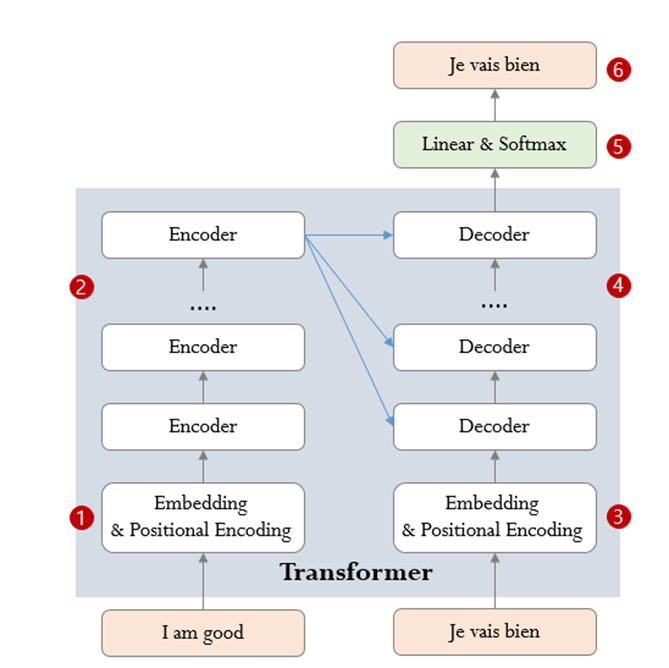
a. 입력 시퀀스(“I am good”)을 임베딩 후 Positional Encoding을 더한 후 Encoder로 입력한다.
b. 입력 시퀀스는 Encoder Stack를 거치면 인코딩된 표현으로 변환된다.
c. 타겟 시퀀스의 시작에 Start of Sentence 토큰을 알리는”< sos >”을 포함한 타겟 시퀀스를 임베딩 후 Positional Encoding을 더한 후 Decoder로 입력한다.
Teacher Forcing
Decoder의 학습과정에서 우리는 예측을 한 Output 값을 사용해서 다음 단어를 예측하는 것이 아니라, 정답 데이터 정보를 이용해서 각 Position의 단어들을 예측하는 방법을 사용한다 즉, 정답이 Input 값이다 이 때문에 우리는 다음 값을 가리는 Masking과정을 거친다.
만약에 예측한 값을 Input으로 사용한다면 언어모델이기 때문에 앞에 잘못된 예측이 뒤에 예측에도 심각한 영향을 줄 수 있다( 첫 단추를 잘못 끼웠는데 두번째 세번째 단추를 올바르게 끼울 수 없기 때문에)
d. Decoder Stack은 Encoder Stack에 의해 인코딩된 표현을 이용하여 타겟 시퀀스의 인코딩된 표현을 생성한다.
e. Linear 레이어와 Softmax 레이어를 통과하면 단어의 확률을 계산하여 최종 출력 시퀀스로 변환한다.
f. Transformer의 Loss 함수는 e단계에서 생성된 출력 시퀀스와 학습 데이터(“Je vais bien”)과 비교하고 back-propagation를 통해 학습한다.
잘 생각해보면 Transformer 또한 신경망의 한 종류라고 생각될 수 있다 Back-Propagation또한 크게 다르지 않다(Gradient의 전파)고 생각할 수 있다
Transformer의 추론과정
Transformer의 추론과정에는 Encoder Stack에 전달되는 입력 시퀀스만 있고
Decoder Stack에 입력할 타겟 시퀀스없이 출력 시퀀스를 생성하는 것이 목표이다
Seq2seq와 비교했을 때, 이전 단계에 생성된 출력 시퀀스를 Decoder Stack의 입력으로 사용하는 것은 동일하나 seq2seq가 이전 단계에서 생성된 단어를 전달하는 반면, Transformer는 누적된 전체 출력 시퀀스를 전달한다.
(seq2seq도 펼치기 전에는 하나의 RNN Layer일 뿐임)
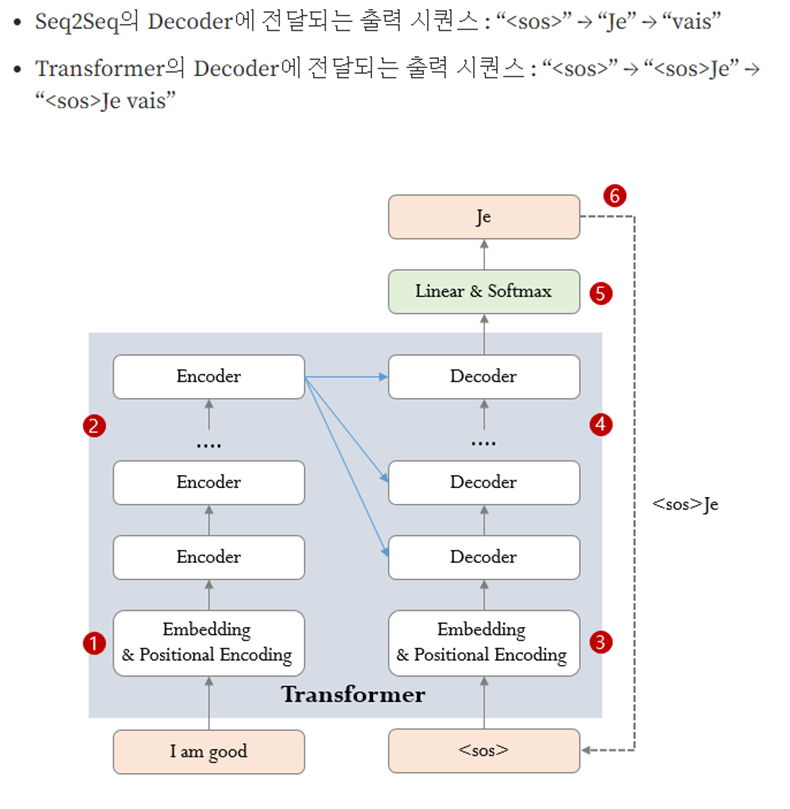
a. 입력 시퀀스(“I am good”)을 임베딩 후 Positional Encoding을 더한 후 Encoder로 입력한다.(훈련과 동일)
b. 입력 시퀀스는 Encoder Stack를 거치면 인코딩된 표현으로 변환된다.(훈련과 동일)
c. 타겟 시퀀스가 없이 시퀀스만을 임베딩 후 Positional Encoding을 더한 후 Decoder로 입력한다
d. Decoder Stack은 Encoder Stack에 의해 인코딩된 표현을 이용하여 타겟 시퀀스의 인코딩된 표현을 생성한다.(훈련과 동일)
-> 인코딩된 표현을 생성한다: 문맥을 담고 있는 벡터를 생성한다
e. Linear 레이어와 Softmax 레이어를 통과하면 단어의 확률을 계산하여 최종 출력 시퀀스로 변환한다.(훈련과 동일)
f. 출력 시퀀스의 마지막 단어를 예측 단어로 사용해서 Decoder의 입력 시퀀스의 다음 위치를 채운다 이후 (3)~(6)을 반복해서 End of Sequence가 나올 때 까지 반복한다.
이제 차근차근 Decoder Block의 과정을 살펴 보겠다
1. Masked Multi-head Attention
“오늘은 금요일이야”를 This is Friday로 번역하는 경우를 생각해보자 여기서 Target 값은 This is Friday일 것이다 우리는 이 Target 값을 ‘’ ‘This’ ‘is’ ‘Friday’로 나누고 이를 임베딩한 이후 Positional Encoding을 더해서 Decoder에 입력 값으로 집어넣을 수 있다 이렇게 집어넣어진 Matrix는 각각 ,,가 곱해져서 Query Key Value로 바뀌게 되고 이렇게 바뀐 Q,K,V에 Multi-head attention을 적용한다
하나의 head에 대해서 보면
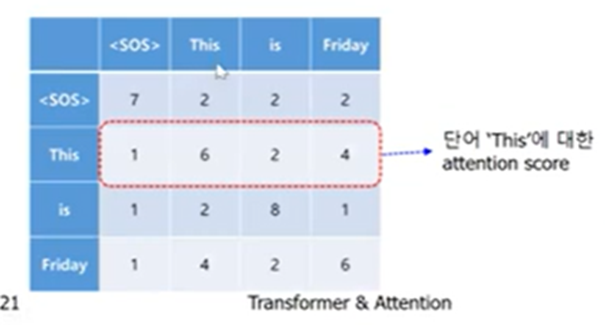
다음과 같은 Attention Score가 나오고 Decoder는 언어모형 이기 때문에
특정단어의 Attention Score 중에서 자기 자신 다음에 나오는 단어에 대한 정보를 사용할 수 없다 .
(실제로 우리가 활용 하고 싶은 Task는 어떤 문장을 입력하면 그 문장을 번역해주는 역할을 수행하고 싶은 것인데 미래의 값에 대한 정보를 가지고 있으면 안된다.)
따라서 특정 단어 이전에 대한 정보만을 사용해서 Attention Score를 구하고 그 정보를 이용해서 계산된 가중치를 Value 벡터에 곱해서 Attention 결과물을 얻어야 한다.
이를 위해서 우리는 attention score를 구하고 특정단어 이후에 나오는 attention score를 -infinite로 대체한다 그러면 Softmax를 취했을 때 결과값이 0이된다.
이렇게 된 이후 Value 벡터를 곱하면 행렬의 첫번째 행은 Value1에 대한 정보만 있고,
두번째 행은 Value1,Value2에 대한 정보 세번째 행은 Value1,Value2,Value3에 대한 정보만을 갖는다 and so on ..
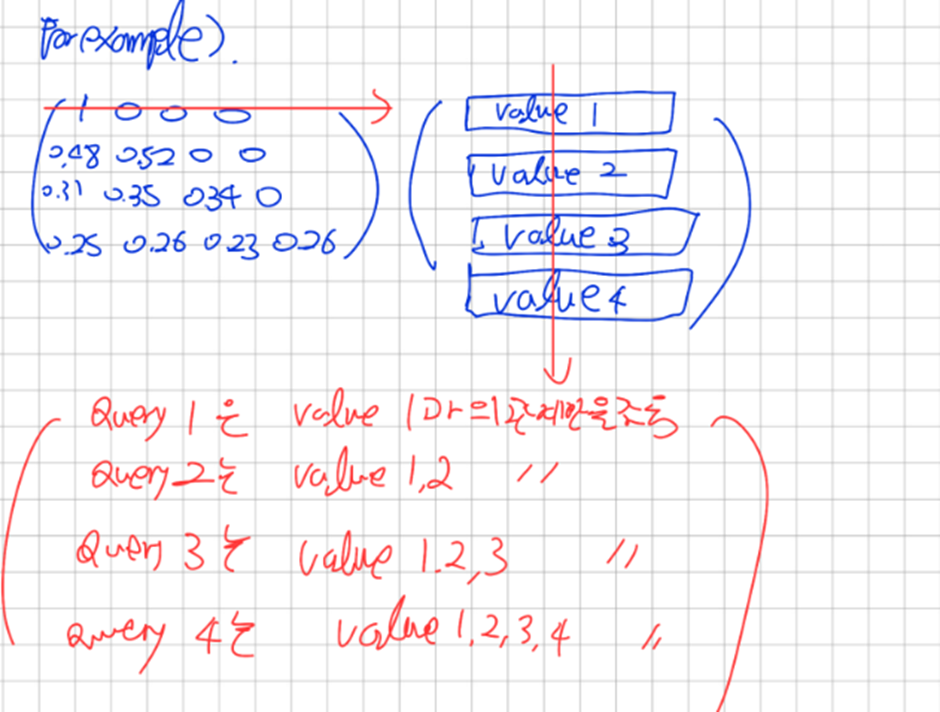
나머지 head에 대해서도 수행후 Concatenate를 한 이후에 Output 행렬을 내면 마찬가지로 첫번째 행은 Value1에 관한 벡터 두번째 행은 Value1,Value2에 대한 정보 세번째 행은 Value1,Value2,Value3에 대한 정보만을 갖는다 and so on ..
2. Add& Norms의 과정을 거친다
3. Encoder-decoder attention 과정
Self-Attention과 마찬가지로 Query, Key, Value를 사용하는데
여기서 Query는 sub layer의 Output 값에 를 곱해서 Q로 만들어주고
Key Value는 Encoder의 마지막 Encoder block에서 출력하는 값에 , 를 곱해서 만들어 준다
작동방식은 Self-Attention과 같다
4. 이후 Add&Norm의 과정을 거친다.
5. Linear&Softmax과정
Linear Layer은 Decoder의 Output을 받아서 모델이 알고 있는 모든 단어들에 대해서 Logit을 생성하고 Softmax를 통해 모델이 알고 있는 모든 단어들에 대해서 모든 단어들에 대한 확률 값을 출력한다 가장 확률이 높은 값을 다음 출력 값으로 내보낸다.
