로지스틱 회귀
실습 예제
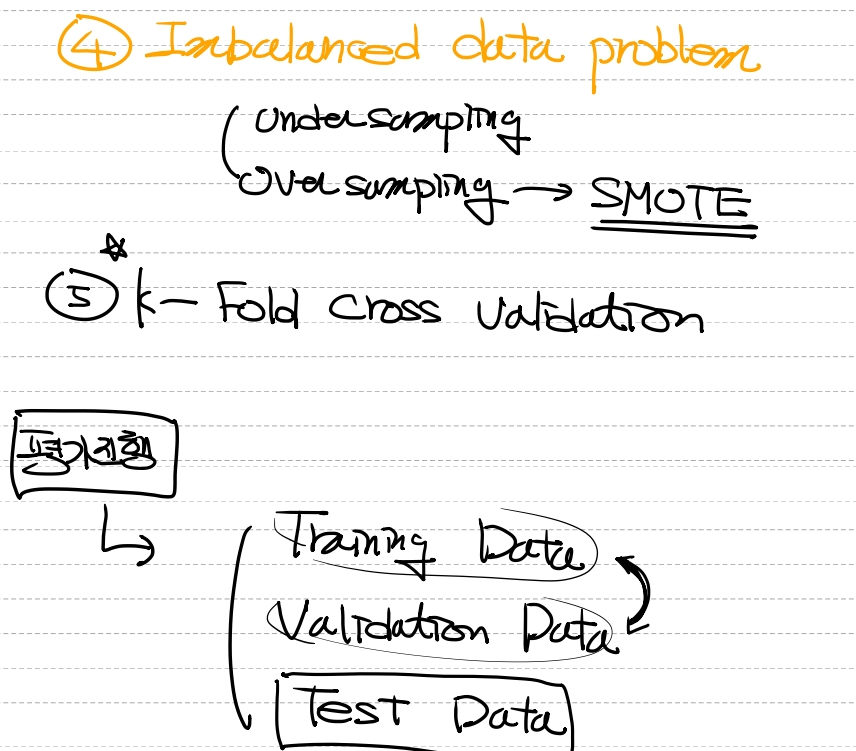
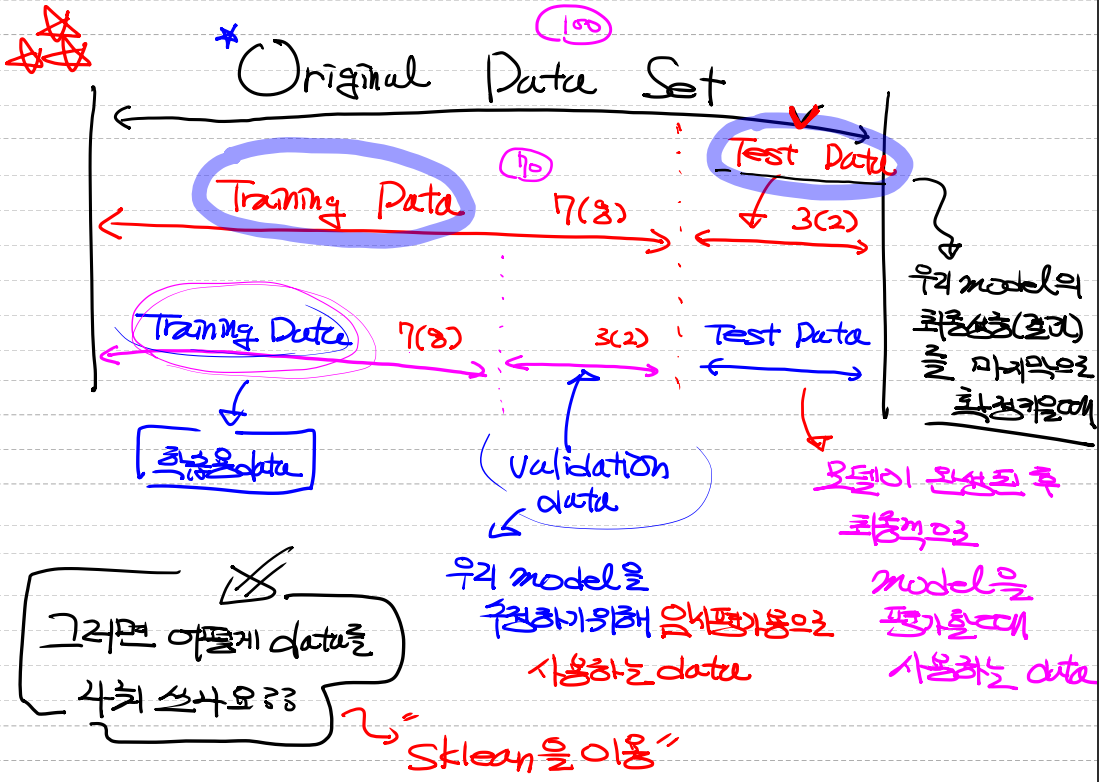
- 만든 모델이 좋은지 안좋지 판단하는것은 평가를 진행하면 됩니다.
- 데이터를 분할해서 학습하고 평가를 진행합니다
- 학습에 사용된 데이터는 평가에 사용하지 않습니다

분류 모델 성능 평가지표
오차행렬(Confusion Matrix)
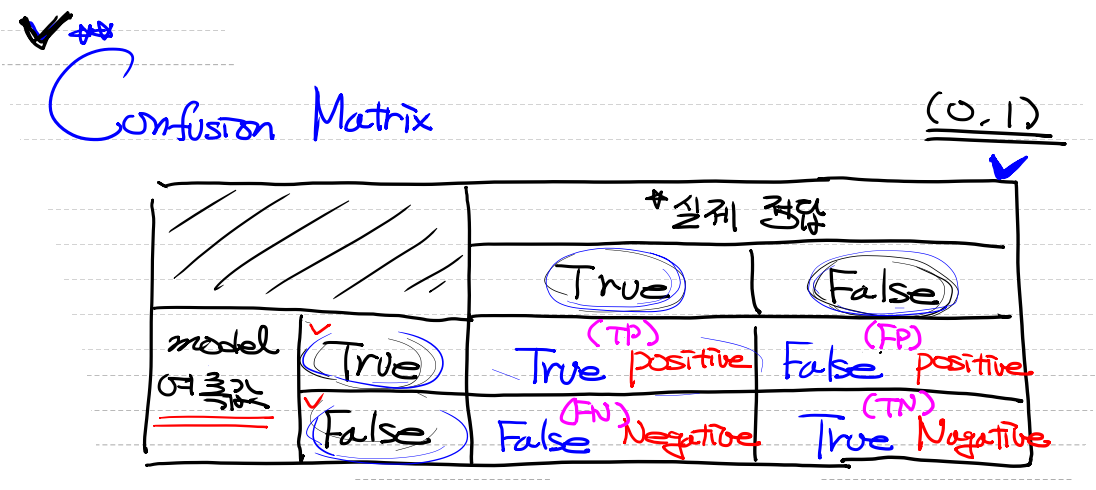
- 실제 정답이 True(1) => True
- 실제 정답이 False(0) => False
- 모델의 예측값이 True(1) => Positive
- 모델의 예측값이 False(0) => Nagative
TP,와TN은 실제값을 맞게 예측한 부분이고,FP와FN은 실제값과 다르게 예측한 부분을 의미한다. 모델 평가 기준에 사용됩니다.
모델 평가 기준
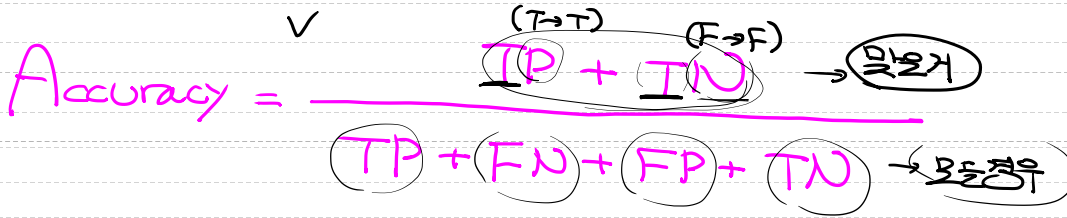
1. 정확도(Accuracy) : 전체 중 모델을 바르게 분류한 비율입니다.
-
가장 직관적인 성능 평가 지표입니다.
-
단점으로는 데이터의 편향이 심한 경우 오류가 발생할 수도 있습니다.
-
ex) 희귀병환자 데이터에서 모델은 0을 출력할 때가 더 많습니다.
2. 재현률(Recall, hit rate)
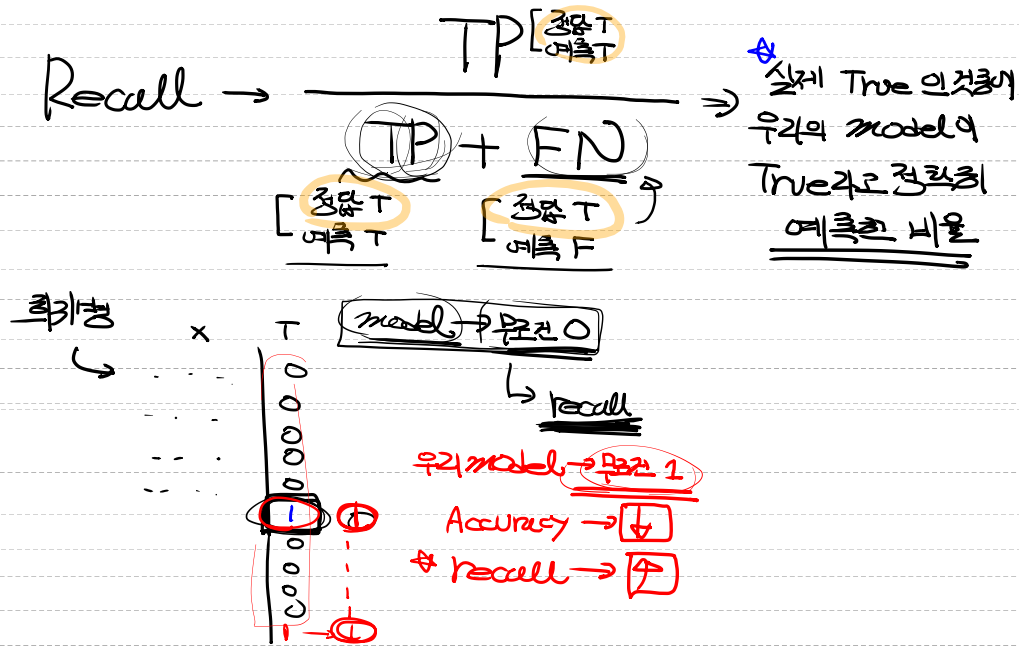
- 실제 값이 True인 것 중 모델이 True라 분류한 비율입니다.
- 위의 오차행렬에서 행방향에 해당하는 부분을 분모로 사용합니다.(TP / TP + FN) (정답 + 정답)
- ex) 희귀병환자 데이터에서 우리의 recall 모델은 무조건 1이라고 판단한다.
3. 정밀도(Precision)
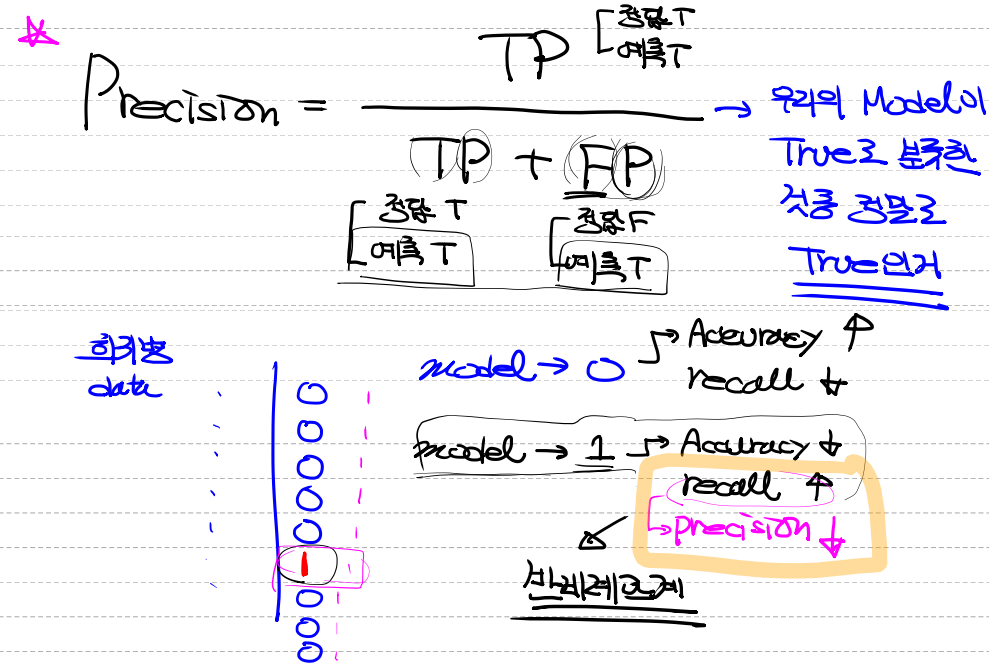
- 모델이 True 로 분류한것 중 실제값이 True인 비율입니다.
- recall과 헷갈릴수 있습니다. 실제 오차행렬에서 열방향에 해당하는 부분을 분모로 사용합니다. (TP / TP + FP) (예측 + 예측)
- recall의 관계와는
반비례관계를 가지고 있습니다
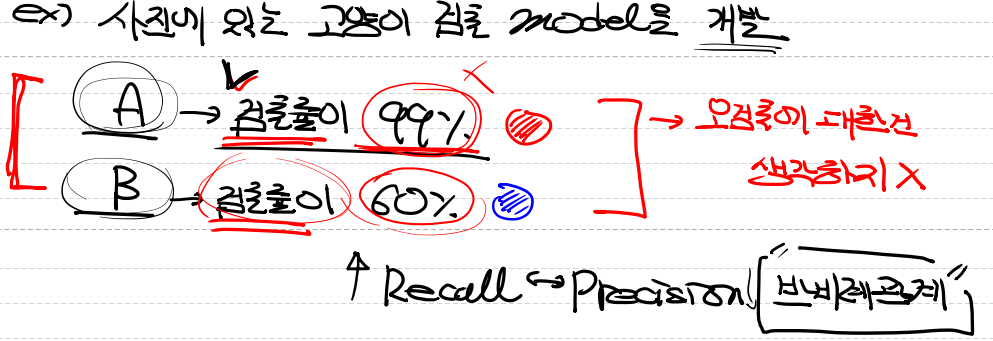
- A모델에서는 검출률이 99%, B모델에서는 검출률이 60%라고 했을때
- 어느 모델이 좋은지는 검출률만보고 판단하기 어렵습니다.
- 이유는 A와 B둘다 오검출을 고려하지 않았기때문입니다.
- A에서 강아지, 고양이 모든 애완동물을 검출해서 99%가 나온 것일 수도 있기 때문입니다.
- B에서는 고양이만 검출했다고 해도 검출률이 낮기 때문에 모델이 좋은지 판단이 되지 않습니다.4. F1 Score
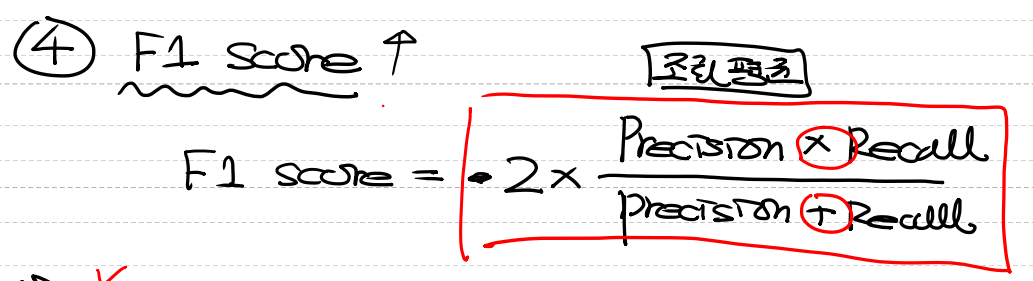
- Precision과 Recall의 조화평균입니다.
- 주로 데이터가 불균형할때 사용합니다
5. Fall-out
- False 중 True로 잘못 예측한 비율입니다.
(FP / FP+ TN) 오차행렬에서 오른쪽의 열부분입니다.
6. ROC curve/AUC
- ROC curve : FPR(fall-out)이 변할 때, TPR(recall)의 변화를 그린 그림입니다.
- FPR을 x축, TPR을 y축으로 그립니다.
- 곡선이 직선 위에 있어야 좋은 모델이고, 직선 아래에 있으면 나쁜 모델, 모델과 함께 직선이면 Random하게 때려맞추는 모델입니다.
- AUC
- ROC곡선 아래의 면적입니다, 1에 가까울수록 좋은 수치입니다.
- 기울기가 1인 직선 아래의 면적이 0.5 -> AUC는 0.5보다 커야합니다.
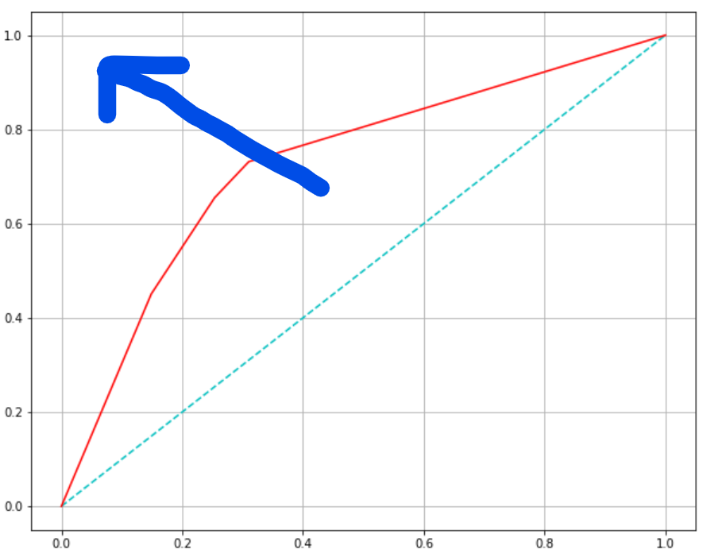
- 초록색 선이 기준이 되는 직선이고, 빨간선인 ROC curve가 직선에서 멀어져 파란 화살표쪽으로 갈수록, 모델의 성능이 좋은 것 입니다.
7. log-loss(cross-entropy)
- 실제 값을 예측하는 확률에 로그를 취하여 부호를 반전시킨 값입니다.
- 즉 ,분류 모델 자체의 잘못 분류된 수치적인 손실값(loss)를 계산합니다.
- log-loss는 낮을수록 좋은 지표이다.추가적으로 알아야하는 사항들
1. Learning rate
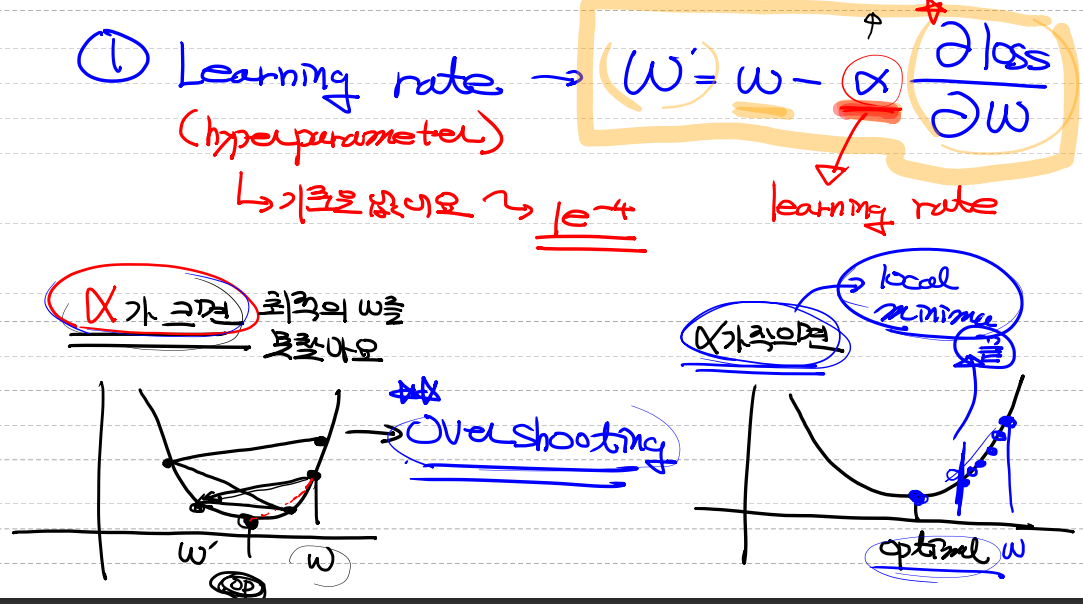
- hyperparameter로 사용하고 기준은 없지만 대부분 1e-4로 시작한다.
- 미분, 경사하강법에 사용이되고, 알파가 크면 최적의 W를 못찾게 된다.
- 이런 현상을 `Overshooting`이라고 한다.
- 반대로 알파가 작게되면 학습이 적게되어 그것보다 더 좋은 값이 있는데 진행이 되지 못하고 멈추는 것을 말합니다.
- 이런 값을 `local minimum`이라고 합니다.2. 정규화(Normalization)
- 머신러닝을 할 때, 입력데이터를
0 ~ 1사이의 값으로 만드는 것- 모든 feature의 scale을 동일하게 만든다.
- overfitting을 피하고 Noise를 감소시켜준다.
- 방법
- Min-Max Normalizaiton(최대, 최소법)
- standardization(평균, 표준편차)
3. Overfitting
- 과적합
- 과대적합(overfitting) : 데이터 모델이 너무 잘 들어맞아서 문제다.
- 과소적합(underfitting) : 모델 학습이 안됐습니다. (큰 문제 X)
Overfitting 해결법
- Training data set에 아주 적합한 모델이지만 실제 데이터에는 적용이 잘 안되는 경우를 말합니다.
- 거의 항상 발생합니다. (정도를 줄이는것이 매우 중요합니다.
-
많은 Training Data를 사용
- Overfitting의 주된 이유는 데이터가 희박하기 때문입니다.
-
독립변수(Feature)의 개수를 줄입니다 -> 다중공선성 문제해결다중공선성이란 독립변수가 독립변수에 상관 영향이 높아 모델에 영향을 주는것을 말합니다.
-
Deep LearningDropout기법을 사용합니다.
-
규제(Regularization)- Weight값이 너무 커지지 않도록 인위적으로 조절합니다.
- L1규제, L2규제 2가지가 있고 수식이 다릅니다.
-
데이터 비대칭 문제(Imbalanced Data Problem)undersampling: 데이터의 개수를 줄이는 방법.
- 90개의 데이터 -> 20개의 데이터
oversampling: 데이터의 개수를 늘리는 방법.
- 복제 : 같은 데이터가 많아져서 overfitting 가능성
- 합성 데이터를 생성 -> SMOTE 알고리즘 사용
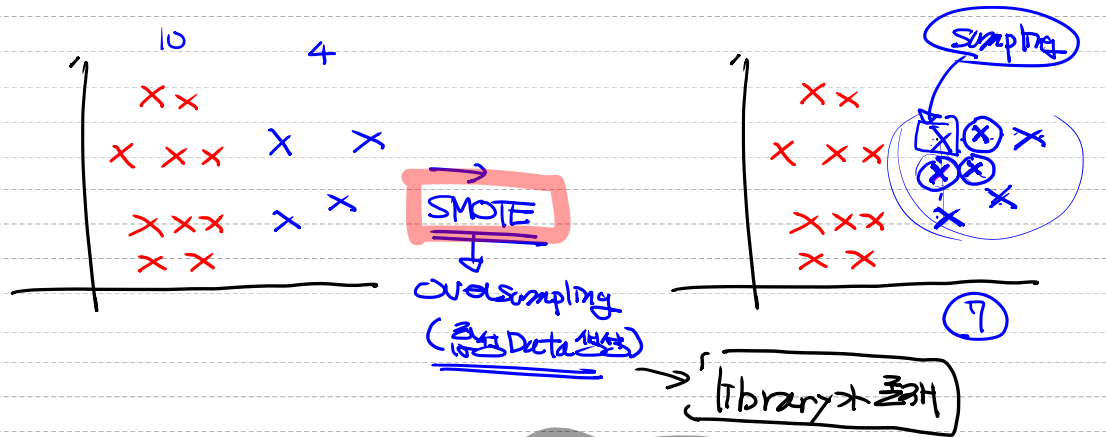
- 합성 데이터를 생성 -> SMOTE 알고리즘 사용
-
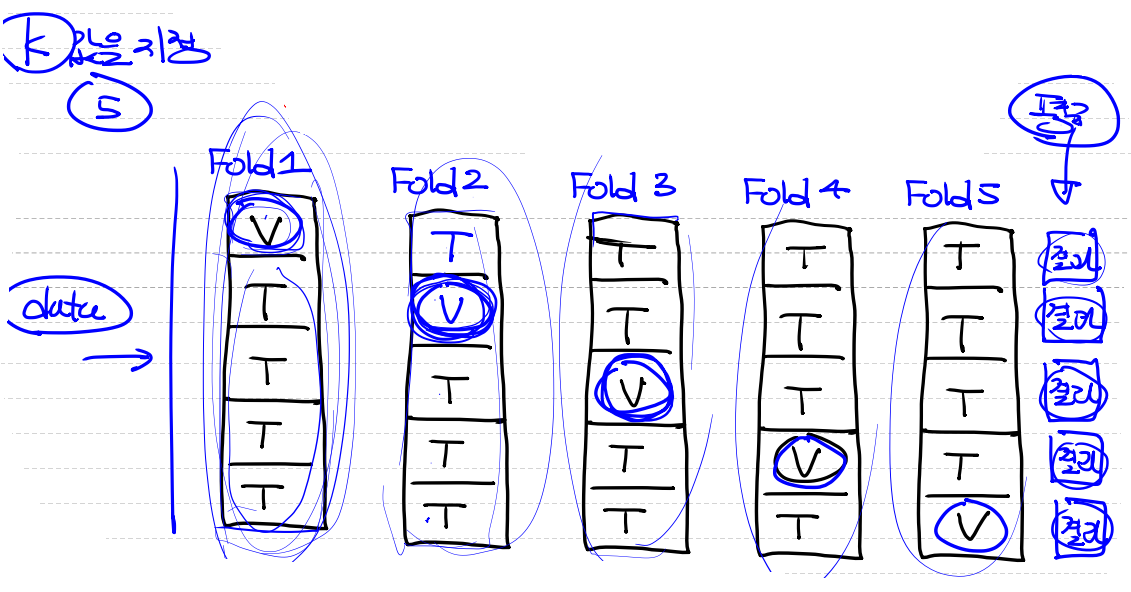
K-Fold Cross Validation- validation data set이 가지고 있는 bias 문제를 해결할 수 있다.
- 적은 데이터를 이용해서 validation이 가능하다.
- 하지만 시간이 오래걸리는 단점이 존재한다.
- ex) K의 값을 5라고 지정하면 Fold가 5개가 생기고 이것을 통과해서 결과값의 평균을 낸다.
파이썬 구현
1. 필요한 module import
# Logistic Regression을 구현해 보아요!
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 이상치 처리를 위한 import
from scipy import stats
# 정규화 진행을 위한 import
from sklearn.preprocessing import MinMaxScaler
from sklearn import linear_model
# keras import
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Flatten, Dense
from tensorflow.keras.optimizers import SGD2. 데이터 로드 및 전처리
# Raw Data Loading
df = pd.read_csv('/content/drive/MyDrive/Colab Notebooks/ML/data/admission/admission.csv')
# display(df) # 400 rows × 4 columns
# 결측치 부터 알아보아요!
df.info()
df.isnull().sum()
# # Column Non-Null Count Dtype
# --- ------ -------------- -----
# 0 admit 400 non-null int64
# 1 gre 400 non-null int64
# 2 gpa 400 non-null float64
# 3 rank 400 non-null int64
# 결측치는 존재하지 않네요!
# 이상치도 알아보아야 해요!
# 이상치를 눈으로 확인하려면 boxplot을 그려보면 되요!
fig = plt.figure()
fig_gre = fig.add_subplot(1,3,1)
fig_gpa = fig.add_subplot(1,3,2)
fig_rank = fig.add_subplot(1,3,3)
fig_gre.boxplot(df['gre'])
fig_gpa.boxplot(df['gpa'])
fig_rank.boxplot(df['rank'])
plt.tight_layout()
plt.show()
# 수치상 이상치로 표현이 되지만
# 실제 데이터예요!(이상치가 아니예요!)
# 하지만 우리학습을 위해 이상치로 판별된 데이터를 삭제하고 진행
zscore_threshold = 2.0 # zscore 임계값 -2이하, 2이상이면 이상치
for col in df.columns:
outlier = df[col][np.abs(stats.zscore(df[col])) > zscore_threshold]
df = df.loc[np.isin(df[col], outlier, invert=True)]
print(df.shape) # (382, 4) 18개의 데이터가 이상치로 제거!
# 정규화를 진행해야 해요!
x_data = df.drop('admit', axis=1, inplace=False).values
t_data = df['admit'].values.reshape(-1,1)
scaler = MinMaxScaler()
scaler.fit(x_data)
x_data_norm = scaler.transform(x_data)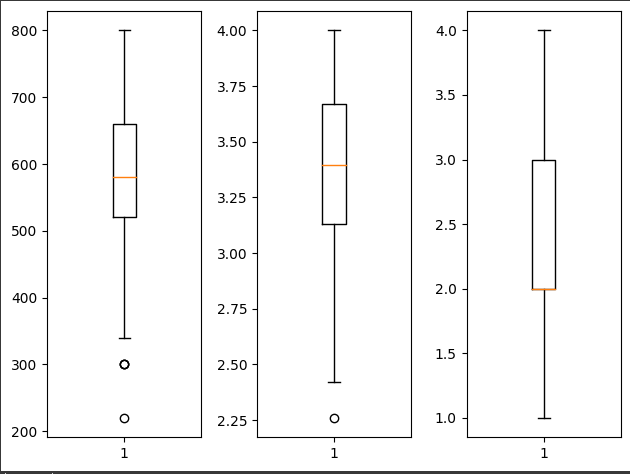
3. sklearn, Tensorflow 구현
# Model을 구현해 보아요!
# sklearn부터 구현해 보아요!
sklearn_model = linear_model.LogisticRegression()
sklearn_model.fit(x_data,
t_data.ravel())
# predict
predict_value = np.array([[600, 3.8, 1]])
result_proba = sklearn_model.predict_proba(predict_value)
print(result_proba) # [[0.43740782 0.56259218]]
----------------------------------------------------------
# Tensorflow로 구현해 보아요!
keras_model = Sequential()
keras_model.add(Flatten(input_shape=(3,)))
keras_model.add(Dense(units=1,
activation='sigmoid'))
keras_model.compile(optimizer=SGD(learning_rate=1e-4),
loss='binary_crossentropy')
keras_model.fit(x_data_norm,
t_data,
epochs=500,
verbose=0)
# predict
predict_value = np.array([[600, 3.8, 1]])
predict_value_norm = scaler.transform(predict_value)
result = keras_model.predict(predict_value_norm)
print(result)
# sklearn : [[0.43740782 0.56259218]]
# tensorflow : [[0.57682455]]12.04 총 정리