🎲[AI] Deep Neural Network가 필요한 이유

해당 글은 FastCampus - '[skill-up] 처음부터 시작하는 딥러닝 유치원 강의를 듣고,
추가 학습한 내용을 덧붙여 작성하였습니다.

---

1. Linear 모델의 한계

• 세상에는 선형 관계로는 해석할 수 없는 비선형 데이터들이 넘쳐남
  e.g. 이미지, 텍스트, 음성, ...
• 이러한 데이터들을 학습하기 위해서는 Linear Regression model이나 Logistic Regression model과 같은 shallow model로는 부족함
• 물론 deep model이라고 해도 layer만 더 깊어질 뿐이지 gradient descent, Loss function 등의 개념은 그대로 사용됨
  
• 고차원의 데이터들은 ploting도 어려움

---

2. Linear + Linear로는 안 될까?

• 여전히 linear함

---

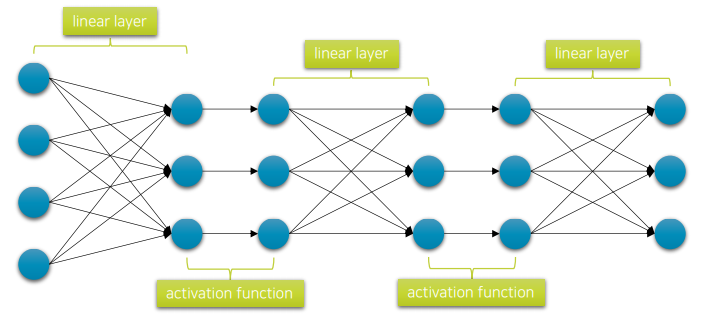
3. Adding Non-linearity

• 만약 layer 사이에 비선형 활성 함수를 넣어 깊게 쌓는다면?
  (꼭 sigmoid, tanh일 필요는 없음)
• 활성함수만 들어가면 비선형 모델을 근사할 수 있음
• 이미 수학적으로 증명된 결과 (보편 근사 정리, UAT)
• DNN은 non-convex한 loss surface를 가짐
  • non-convex: 표면에 봉우리(peak), 골짜기(valley), 안장점(saddle point) 등이 많이 존재하는 곡면
    

보편 근사 정리 (UAT, Universal Approximation Theorem)
"충분한 수의 뉴런과 적절한 비선형 활성함수가 있다면, 하나의 은닉층만으로도 어떤 연속적인 함수든 원하는 정확도로 근사할 수 있다."

• 선형 함수만 여러 개 쌓으면 결국 전체 모델도 선형이 됨
• 하지만 중간에 비선형 함수 (예: ReLU, sigmoid)를 넣으면 모델은 비선형 함수도 표현할 수 있게 됨
• 비선형 활성함수를 가진 충분히 큰 신경망은 어떤 함수든 근사할 수 있다는 수학적 보장
• 수식
  
  임의의 연속 함수$f: \mathbb{R}^n \rightarrow \mathbb{R}$ 와
  임의의 작은 오차 $\varepsilon > 0$ 에 대해,
  다음과 같은 구조의 함수$\hat{f}(\mathbf{x}$) 가 존재한다면:
  $\hat{f}(\mathbf{x}) = \sum_{i=1}^{N} \alpha_i \cdot \sigma(\mathbf{w}_i^\top \mathbf{x} + b_i)$
  이때,
  $\| f(\mathbf{x}) - \hat{f}(\mathbf{x}) \| < \varepsilon \quad \forall \, \mathbf{x} \in K$
  K는 compact한 입력 공간 (즉, 유계 폐집합)이다.
  
  $\mathbf{x} \in \mathbb{R}^n$ : 입력 벡터
  $\sigma(\cdot)$ : 비선형 활성 함수 (예: sigmoid, tanh)
  $\alpha_i \in \mathbb{R}$ : 출력 가중치
  $\mathbf{w}_i \in \mathbb{R}^n$ : 입력 가중치
  $b_i \in \mathbb{R}$ : 바이어스
  $N \in \mathbb{N}$ : 은닉 뉴런의 수 (충분히 크면 가능)
  $\hat{f}(\mathbf{x})$ : 신경망이 근사한 함수

---

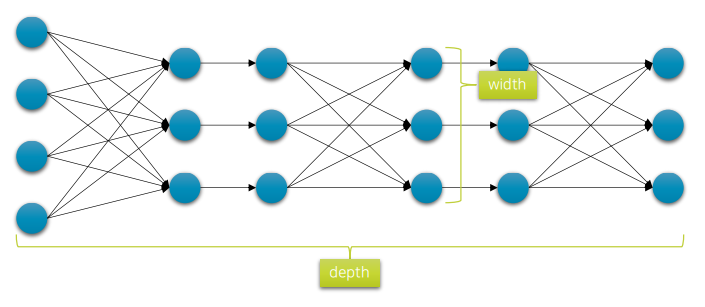
4. Network Capacity

• 깊이(depth)와 너비(width)를 넓게 할수록 신경망의 표현력은 좋아진다.
  → 복잡한 형태의 함수를 학습할 수 있는 능력이 생김
• 일단 깊고 넓게, learing rate를 작게 하면 뭐라도 만들어지긴 함
  

---