🎲[AI] LinearRegression

해당 글은 FastCampus - '[skill-up] 처음부터 시작하는 딥러닝 유치원 강의를 듣고,
추가 학습한 내용을 덧붙여 작성하였습니다.

1. Motivation

• 우리의 목표는 주어진 데이터를 바탕으로 결과를 반환하는 함수를 모사하는 것
• 세상에는 선형적인 관계를 가지는 데이터가 많음
  • 예: 키 vs 몸무게, 나이 vs 연봉, 무게 vs 가격, 연식 vs 가격

---

2. 문제 정의

• 입력 x가 주어졌을 때, 그에 맞는 출력 y를 예측할 수 있는 함수를 학습하자
• 선형 관계를 가정할 수 있는 데이터셋에 대해, 예측 모델을 만든다

---

3. 선형 회귀 모델

• 모델 식: y = xW + b

  • x: 입력 벡터 (feature)
  • W: 가중치 행렬
  • b: 편향 벡터
  • y: 예측 결과

• 목적: 실제 y와 예측값 ŷ 사이의 오차를 최소화하는 W, b를 찾는 것

---

4. 파라미터 최적화 방법 (Gradient Descent 기반)

• 파라미터: θ = {W, b}
• θ를 통해 정의된 예측 함수: $f_θ(x_i)$
• Mean Squared Error (MSE)를 활용한 손실 함수(Loss Function): ${1 \over N} * Σ (y_i - ŷ_i)^2$
• Loss function을 θ에 대해 미분하여 얻은 gradient descent로 θ를 반복적으로 업데이트
  
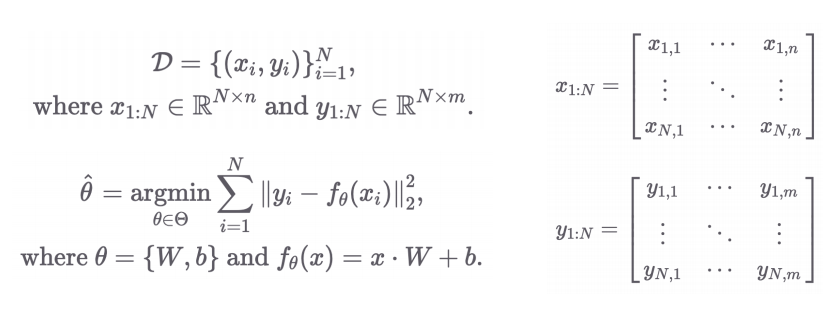
• θ = {W, b}이고, |W| = (n, m), |b| = (m,)
• Loss Function을 θ에 대해 미분한다는 것은, 각각의 $W_{k,i}$ element와 $b_j$ element에 대해 편미분하여 gradient descent를 구하는 것
• 전체 파라미터 θ는 W와 b의 모든 원소를 포함한 하나의 벡터로 생각

---

5. Pytorch 실습 코드

$θ ← θ - η▽_θL(θ)$ x 1,000 iterations
$y = f(x)$
$x ∈ R^{506 X 5}$
$y ∈ R^{506 X 1}$

$D = {(x_i, y_i)}^{N=506}_{i=1}$
$ŷ = f_θ(x) = x*W + b$
$θ = \{W, b\}$
$W ∈ R^{5X1}$
$b ∈ R^{1X1}$
$L(θ) = {1 \over N} * Σ (y_i - ŷ_i)^2$

boston = fetch_openml(name='boston', version=1, as_frame=True)
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df["TARGET"] = boston.target

# df.tail()
# sns.pairplot(df)
# plt.show()

cols = ["TARGET", "INDUS", "RM", "LSTAT", "NOX", "DIS"]

# df[cols].describe()
# sns.pairplot(df[cols])
# plt.show()


data = torch.from_numpy(df[cols].values).float()

print(data.shape)

x = data[:, 1:]
y = data[:, :1]

print(x.shape, y.shape)

n_epochs = 2000 #학습 반복 횟수
learning_rate = 1e-3
print_interval = 100

# x.shape: (batch_size, input features) 
# y.shape: (batch_size, output targets) 
model = nn.Linear(x.size(-1), y.size(-1)) # args: (input features, output features)

optimizer = optim.SGD(model.parameters(), # 확률적 경사 하강법(Stochastic Gradient Descent)
                      lr=learning_rate)

for i in range(n_epochs):
    y_hat = model(x)
    loss = F.mse_loss(y_hat, y)
    
    optimizer.zero_grad() # gradient 초기화 꼭 해줘야 함! 아니면 더해짐
    loss.backward() # 기울기 구하기    
    optimizer.step() # optimizer에게 구해진 기울기로 파라미터 업데이트 하도록
    
    if (i + 1) % print_interval == 0:
        print('Epoch %d: loss=%.4e' % (i + 1, loss))


torch.cat([y, y_hat], dim=1)

df = pd.DataFrame(torch.cat([y, y_hat], dim=1).detach_().numpy(),
                  columns=["y", "y_hat"])

sns.pairplot(df, height=3)
plt.show()

---