🎲[AI] 기초 최적화 방법 - Gradient Descent

해당 글은 FastCampus - '[skill-up] 처음부터 시작하는 딥러닝 유치원 강의를 듣고,
추가 학습한 내용을 덧붙여 작성하였습니다.

---

1. 미분 (Derivative)

---

1.1 기울기

• 함수 입력값(x) 변화에 따른 출력값(y) 변화 비율
  

---

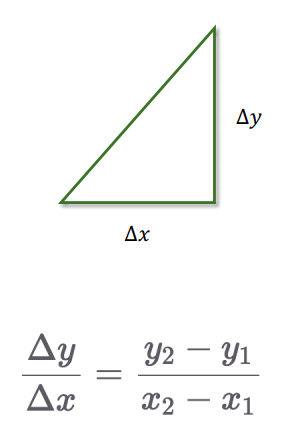
1.2 극한과 접선

• 두 점이 무한히 가까워질 때 접선의 기울기 개념으로 도입
• 미분은 이 접선의 기울기를 구하는 과정
  

---

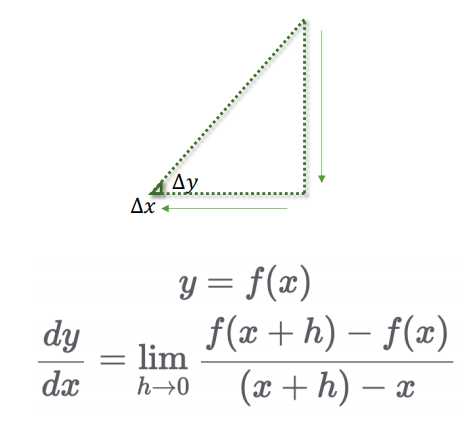
1.3 도함수

• 특정 지점이 아닌 전 범위에 대해 기울기를 일반화한 함수
  

---

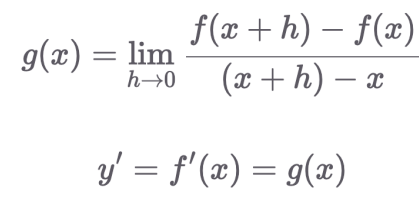
1.4 뉴턴 미분법 vs 라이프니츠 미분법

뉴턴 미분법: 변수가 하나일 때 편리

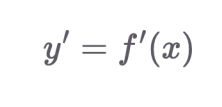
라이프니츠 미분법: 변수가 두 개 이상일 때 편리

---

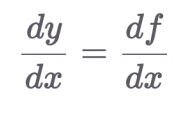
1.5 합성함수 미분

---

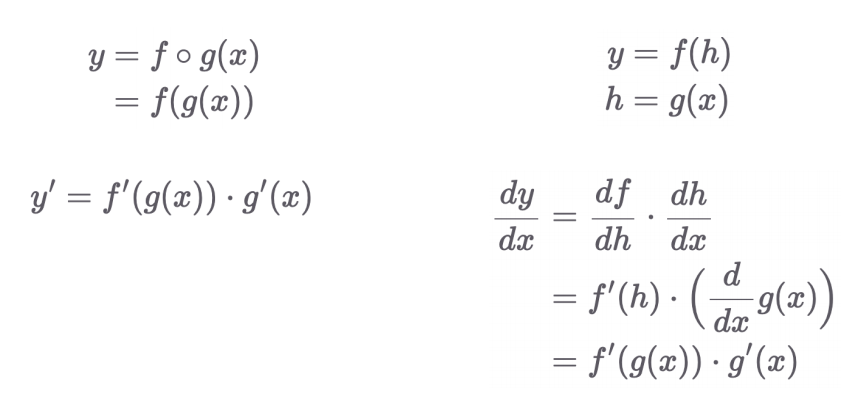
2. 편미분 (Partial Derivative)

---

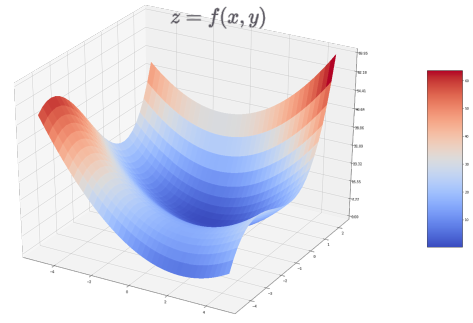
2.1 다변수 함수(Multivariable function)

• 변수가 두 개 이상인 함수
  

---

2.2 편미분이란?

• 다변수 함수에서 하나의 변수만 남기고 나머지를 상수로 간주하고 미분하는 것
• 기호: ∂(Round, Partial)
  

---

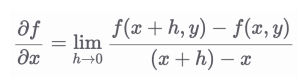
2.3 Gradient 벡터: 고차원 함수의 미분

• 입력/출력이 벡터 또는 행렬일 때도 각각 편미분 가능
• 기호: ▽(nabla, del)
• 결과는 gradient 벡터로 표현되며 방향과 크기 모두 포함
• 즉, gradient 벡터는 각 변수에 대한 편미분을 모아놓은 벡터
  

---

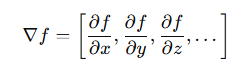
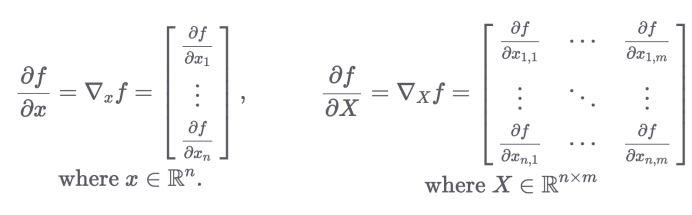
2.4 왜 Gradient 벡터가 필요할까?

• Loss라는 스칼라 값을 파라미터 행렬로 미분하고 싶다!
  

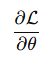
• DNN의 중간 결과물 벡터를 파라미터(가중치) 행렬로 미분해야 한다면?
  

---

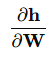
2.5 Pytorch의 Autograd 기능

x = torch.FloatTensor([[1, 2],
                       [3, 4]])
x.requires_grad = True
                       
x1 = x + 2
x2 = x - 2
x3 = x1 * x2
y = x3.sum() 

y.backward() #y가 scalar여만 backward 가능
print(x.grad)
                   

---

3. Gradient Descent 알고리즘

---

3.1 Gradient Descent 알고리즘이란?

• Loss 값이 최소화되는 파라미터 θ를 찾는 알고리즘
• 즉, 주어진 데이터에 대해 출력값이 잘 맞는 함수를 찾기 위한 알고리즘

---

3.2 1D 예시

• x에 대해 미분한 기울기를 이용해 낮은 방향으로 이동
  
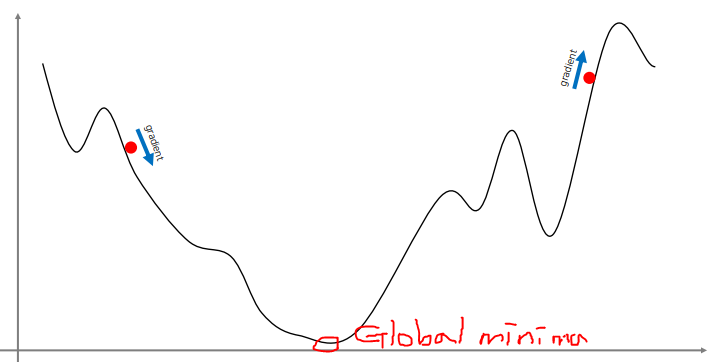
• 가장 loss가 낮은 곳(Globla minima)이 아닌 골짜기(Local minima)에 빠질 가능성이 있음
• 사실 지금 찾은 minima가 global minima일 것이라고 보장할 순 없다
• Gradient Descent Equation
  
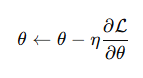
• L: Loss function (scalar)
• θ: Parameters (vector)
• η: Learning Rate (경험적으로 지정해주는 Hyper parameter 0 ~ 1)
• Loss를 각 파라미터에 대해 편미분한 gradient 벡터를 통해 모든 파라미터를 동시에 업데이트

---

3.3 고차원 확장

• θ(W,b)가 다차원일 때도 동일 원리 적용
• 2차원인 경우
  
  
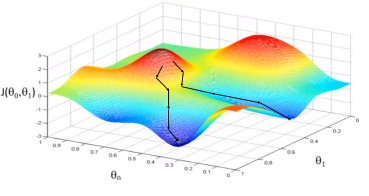
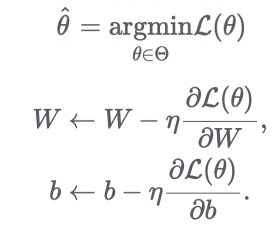
• 딥러닝에서는 수백만 개의 파라미터가 존재 → local minima에 빠질 가능성은 적음
  • 수백만, 수천, 수억만 차원의 loss 함수 surface에서 global minima를 찾는 문제에서,
  • 동시에 local minima를 위한 조건이 만족되기는 어렵기 때문
  • 따라서, local minima에 대한 걱정을 크게 할 필요 없음

---

3.4 Pytorch로 구현해보기

import torch
import torch.nn.functional as F

target = torch.FloatTensor([[.1, .2, .3],
                            [.4, .5, .6],
                            [.7, .8, .9]])

x = torch.rand_like(target)
x.requires_grad = True
loss = F.mse_loss(x, target)

### start ###
threshold = 1e-5
learning_rate = 1.0
iter_cnt = 0

while loss > threshold:
    iter_cnt += 1
    
    loss.backward() # Calculate gradients.

    x = x - learning_rate * x.grad
    
    x.detach_() # autograd graph 끊어주기
    x.requires_grad_(True)
    
    loss = F.mse_loss(x, target)
    
    print('%d-th Loss: %.4e' % (iter_cnt, loss))
    print(x)

---

4. Learning Rate

---

4.1 Learning Rate의 역할

• 학습 시 파라미터 업데이트 크기를 결정하는 step size
• 적절하지 않으면 loss가 발산하거나 수렴 속도가 느려짐

---

4.2 Learning Rate의 최적화

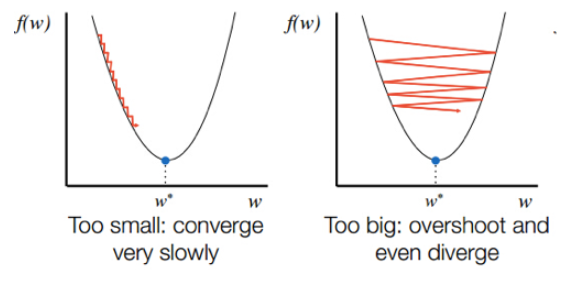
• 너무 큰 learning rate → 발산(Loss가 inf, NaN이 나옴)
• 너무 작은 learning rate → 너무 느린 수렴, local minima에 머무를 수 있음(파라미터가 많으면 주로 발생 X)
  

---

4.3 Learning Rate Tip

• 모델에 따라 적절한 값이 달라지며, 절대적인 기준은 없음
• 내 모델에 적절한 하이퍼 파라미터를 찾을 수 있도록 실험을 통해 최적화하는 것이 필요
• 적절한 값을 찾기 어렵다면 1e-4 같이 작은 값을 사용하고 오래 학습
• Adam Optimizer 등으로 자동 조정도 가능

---

5. Summary

1. 알 수 없는 참 함수를 근사하기 위해 모델을 학습시킴
2. 손실함수를 줄이는 방향으로 파라미터를 업데이트
3. 이를 위해 기울기(gradient)를 계산하고
4. 학습률(learning rate)을 곱해 업데이트 진행

• Gradient Descent는 손실을 최소화하기 위한 기본적인 최적화 알고리즘이다.