🎲[AI] 다중 분류, Softmax, Cross Entropy

해당 글은 FastCampus - '[skill-up] 처음부터 시작하는 딥러닝 유치원 강의를 듣고,
추가 학습한 내용을 덧붙여 작성하였습니다.

---

1. 다중 분류 (Multi-class Classification)

• 입력값 x에 대해 여러 클래스 중 하나를 예측하는 문제
• 출력은 확률 벡터이며, Softmax 함수를 통해 각 클래스에 대한 확률을 구함
• 클래스 별 확률 값들을 전부 더하면 1
• 예측 결과는 가장 높은 확률을 가진 클래스 선택
  

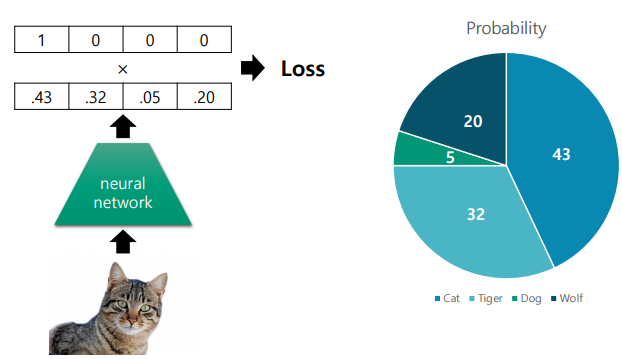
이진 분류 (Binary classification)

• Sigmoid의 출력 값은 0 ~ 1이므로, 확률 값 P(y|x)으로 생각해볼 수 있음.
• 신경망은 True 클래스의 확률 값을 뱉어낸다고 정의하여 Classificaiton을 확률 문제로 치환할 수 있음

---

2. Softmax 함수

• 입력 벡터를 discrete(이산) 확률 분포로 변환하는 함수
• 모든 클래스 확률의 합은 1
• 수식:

$softmax_i(x) = {exp(x_i) \over \sum_{j=1}^n exp(x_j)}$

• 분류기 출력은 각 클래스에 대한 확률 벡터로 해석됨

$softmax(x) = [softmax_1(x) ... softmax_n(x)]$

One-hot encoding

• 하나의 값만 1이고 나머지는 0인 벡터로 표현하는 방식
• ex)
  Dog [1, 0, 0]
  Cat [0, 1, 0]
  Bird [0, 0, 1]
• 카테고리 수가 많아지면 벡터가 고차원(sparse) → 메모리 비효율
• 대안으로는 embedding 방법이 많이 쓰임 (특히 딥러닝에서)

항목	One-hot Encoding	Embedding
표현 방식	0과 1의 희소 벡터	연속적인 실수 벡터
차원	클래스 개수만큼 (보통 매우 큼)	하이퍼파라미터로 지정된 저차원 (예: 5차원)
정보량	의미 없음 (순서·유사도 無)	유사도, 의미를 벡터 공간에 반영
메모리 효율	매우 비효율적 (sparse)	효율적 (dense)
예시	[1, 0, 0], [0, 1, 0], [0, 0, 1]	[0.12, 0.3, ..., -0.4], [0.51, ..., 0.06], [0.02, ..., -0.11]

---

3. Cross Entropy Loss

• 다중 클래스 분류에서 사용되는 손실 함수

• Binary Cross Entropy의 일반화 형태

• Softmax와 함께 사용되어 분류 문제에 적합
  $CE(y_{1:N}, ŷ_{1:N}) = {-1 \over N} \sum_{i=1}^Ny_i^T*logŷ_i \\ = {-1 \over N} \sum_{i=1}^N\sum_{j=1}^my_{i,j} *logŷ_{i,j} \\ = {-1 \over N} \sum_{i=1}^N logP_{\theta}(y_i|x_i) \\ where \ y_{1:N} ∈ R^{N, m} \ and\ ŷ_{1:N} ∈ R^{N, m}$

• 실제 정답 클래스에 해당하는 확률값이 높아지도록 학습

---

4. Log-Softmax

• Cross Entropy Loss에서 log 씌워서 계산하는 거 이왕 Softmax에서 씌워줘서 출력 안정성과 수학적 편의성을 가져가자

$log-softmax_i(x) =log{exp(x_i) \over \sum_{j=1}^n exp(x_j)}$

• NLL(Negative Log Likelihood) 사용 가능

$NLL(y_{1:N}, ŷ_{1:N}) = {-1 \over N} \sum_{i=1}^NlogP_{\theta}(y_i|x_i)$

$logP_{\theta}(y_i|x_i)$가 log-softmax의 결과

---

5. Confusion Matrix

• Accuracy, Recall를 통해 모델의 성능을 순서대로 나타낼 수 있음**
• 하지만 하나의 숫자로 나타낸만큼 내부의 자세한 성능을 알 수 없음
  • 특히 클래스 불균형 상황이라면 결과가 외곡될 수 있음
• Confusion Matrix는 실제 클래스 vs 예측 클래스를 표 형태로 표현

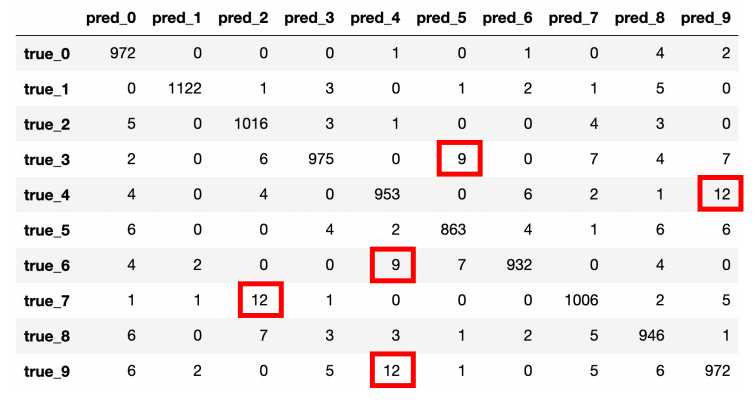
• 어떤 클래스에서 성능이 낮은지를 직관적으로 파악 가능
• 제품 개선, 후속 학습 등에 유용

---

6. 회귀 vs 분류 요약

Task	Output	Activation	Loss Function
Regression	Real Value	Linear (None)	MSE Loss
Binary Classification	0 or 1	Sigmoid	Binary Cross Entropy
Multi-class Classification	Class	Softmax	Cross Entropy Loss

---

7. Summary

• 다중 분류에서는 Softmax와 Cross Entropy를 함께 사용하여 각 클래스별 확률을 예측하고 학습
• Confusion Matrix는 클래스별 예측 성능 분석에 중요한 도구
• Accuracy, recall, F1 Score 등의 정량화된 숫자만 보지 말고, Confusion Matrix를 함께 활용하여 모델 성능을 다각도로 평가할 것

---

8. Pytorch 실습 코드

• MNIST Dataset
• 28 x 28 픽셀 이미지를 784 차원의 벡터로 만듦
  • (70000, 28, 28) → (70000, 784)
• y값은 0~9까지 값이 들어있는 one hot encoded vector의 index가 담겨 있는 것
  • [0,0,0,1,0,0,0,0,0,0] → 3 (메모리 절약)

$x ∈ R^{70000, \ 784}$
$y ∈ R^{70000, \ 10}$

# Classification with Deep Neural Networks

## Load MNIST Dataset

import numpy as np
import matplotlib.pyplot as plt

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import pandas as pd
from sklearn.metrics import confusion_matrix

from torchvision import datasets, transforms

train = datasets.MNIST(
    '../data', train=True, download=True,
    transform=transforms.Compose([
        transforms.ToTensor(),
    ]),
)
test = datasets.MNIST(
    '../data', train=False,
    transform=transforms.Compose([
        transforms.ToTensor(),
    ]),
)

def plot(x):
    img = (np.array(x.detach().cpu(), dtype='float')).reshape(28,28)

    plt.imshow(img, cmap='gray')
    plt.show()

plot(train.data[0])

x = train.data.float() / 255.
y = train.targets
print(x.shape, y.shape)
x = x.view(x.size(0), -1)
print(x.shape, y.shape)

input_size = x.size(-1)
output_size = int(max(y)) + 1

print('input_size: %d, output_size: %d' % (input_size, output_size))

# Train / Valid ratio
ratios = [.8, .2]

train_cnt = int(x.size(0) * ratios[0])
valid_cnt = int(x.size(0) * ratios[1])
test_cnt = len(test.data)
cnts = [train_cnt, valid_cnt]

print("Train %d / Valid %d / Test %d samples." % (train_cnt, valid_cnt, test_cnt))

indices = torch.randperm(x.size(0))

x = torch.index_select(x, dim=0, index=indices)
y = torch.index_select(y, dim=0, index=indices)

x = list(x.split(cnts, dim=0))
y = list(y.split(cnts, dim=0))

x += [(test.data.float() / 255.).view(test_cnt, -1)]
y += [test.targets]

for x_i, y_i in zip(x, y):
    print(x_i.size(), y_i.size())

## Build Model & Optimizer

model = nn.Sequential(
    nn.Linear(input_size, 500),
    nn.LeakyReLU(),
    nn.Linear(500, 400),
    nn.LeakyReLU(),
    nn.Linear(400, 300),
    nn.LeakyReLU(),
    nn.Linear(300, 200),
    nn.LeakyReLU(),
    nn.Linear(200, 100),
    nn.LeakyReLU(),
    nn.Linear(100, 50),
    nn.LeakyReLU(),
    nn.Linear(50, output_size),
    nn.LogSoftmax(dim=-1),
)

model

crit = nn.NLLLoss()

optimizer = optim.Adam(model.parameters())

## Move to GPU if it is available

device = torch.device('cpu')
if torch.cuda.is_available():
    device = torch.device('cuda')

model = model.to(device)

x = [x_i.to(device) for x_i in x]
y = [y_i.to(device) for y_i in y]

## Train

n_epochs = 1000
batch_size = 256
print_interval = 10

from copy import deepcopy

lowest_loss = np.inf
best_model = None

early_stop = 50
lowest_epoch = np.inf

train_history, valid_history = [], []

for i in range(n_epochs):
    indices = torch.randperm(x[0].size(0))
    x_ = torch.index_select(x[0], dim=0, index=indices)
    y_ = torch.index_select(y[0], dim=0, index=indices)
    
    x_ = x_.split(batch_size, dim=0)
    y_ = y_.split(batch_size, dim=0)
    
    train_loss, valid_loss = 0, 0
    y_hat = []
    
    for x_i, y_i in zip(x_, y_):
        y_hat_i = model(x_i)
        loss = crit(y_hat_i, y_i.squeeze())

        optimizer.zero_grad()
        loss.backward()

        optimizer.step()        
        train_loss += float(loss) # This is very important to prevent memory leak.

    train_loss = train_loss / len(x_)
        
    with torch.no_grad():
        x_ = x[1].split(batch_size, dim=0)
        y_ = y[1].split(batch_size, dim=0)
        
        valid_loss = 0
        
        for x_i, y_i in zip(x_, y_):
            y_hat_i = model(x_i)
            loss = crit(y_hat_i, y_i.squeeze())
            
            valid_loss += float(loss)
            
            y_hat += [y_hat_i]
            
    valid_loss = valid_loss / len(x_)
    
    train_history += [train_loss]
    valid_history += [valid_loss]
        
    if (i + 1) % print_interval == 0:
        print('Epoch %d: train loss=%.4e  valid_loss=%.4e  lowest_loss=%.4e' % (
            i + 1,
            train_loss,
            valid_loss,
            lowest_loss,
        ))
        
    if valid_loss <= lowest_loss:
        lowest_loss = valid_loss
        lowest_epoch = i
        
        best_model = deepcopy(model.state_dict())
    else:
        if early_stop > 0 and lowest_epoch + early_stop < i + 1:
            print("There is no improvement during last %d epochs." % early_stop)
            break

print("The best validation loss from epoch %d: %.4e" % (lowest_epoch + 1, lowest_loss))
model.load_state_dict(best_model)

## Loss History

plot_from = 0

plt.figure(figsize=(20, 10))
plt.grid(True)
plt.title("Train / Valid Loss History")
plt.plot(
    range(plot_from, len(train_history)), train_history[plot_from:],
    range(plot_from, len(valid_history)), valid_history[plot_from:],
)
plt.yscale('log')
plt.show()

## Let's see the result!

test_loss = 0
y_hat = []

with torch.no_grad():
    x_ = x[-1].split(batch_size, dim=0)
    y_ = y[-1].split(batch_size, dim=0)

    for x_i, y_i in zip(x_, y_):
        y_hat_i = model(x_i)
        loss = crit(y_hat_i, y_i.squeeze())

        test_loss += loss # Gradient is already detached.

        y_hat += [y_hat_i]

test_loss = test_loss / len(x_)
y_hat = torch.cat(y_hat, dim=0)

print("Validation loss: %.4e" % test_loss)

correct_cnt = (y[-1].squeeze() == torch.argmax(y_hat, dim=-1)).sum()
total_cnt = float(y[-1].size(0))

print('Accuracy: %.4f' % (correct_cnt / total_cnt))



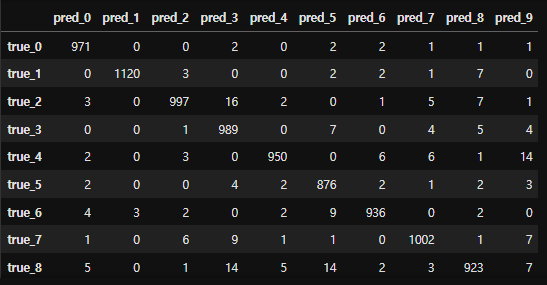
pd.DataFrame(confusion_matrix(y[-1], torch.argmax(y_hat, dim=-1)),
             index=['true_%d' % i for i in range(10)],
             columns=['pred_%d' % i for i in range(10)])

---