[Research Note] When Matrices Go Infinite (2/2) : ML Perspective

Junu Kim·2025년 10월 5일

Linear Algebra Research machine learning matrix

Research Note

목록 보기

2/3

들어가며

이 글은 제가 학부 과정에서 배운 유한 행렬 (finite matrices)의 개념에서 행이나 열의 개수가 무한히 확장된 무한 행렬 (Infinite Matrices)의 개념으로 확장시키는 과정을 공유하기 위해 작성된 두번째 글입니다.

이 글은 추상적인 무한대라는 개념이 어떻게 행렬이라는 개념에 편입되는지 그리고 나아가 ML 아키텍처에서의 활용으로 어떻게 연결되는지 탐구합니다.

Section 1: Mathematical Intuition에서는 무한 행렬의 기본 이론을 소개하고, 이를 바나흐 공간 (Banach space)에서 작용하는 선형 유계 연산자 (linear bounded operators)로 해석하는 직관을 살펴봅니다. 특히, 컴퓨터 계산을 위해 무한 시스템을 유한 시스템으로 근사하고 해의 수렴성을 보장하는 축소 방법 (reduction method)에 집중할 예정입니다.

Section 2: ML Perspective에서는 이 무한 개념이 머신러닝에 어떻게 적용되는지 조명합니다. 특징 상호작용 공간 (feature interaction space)의 차원을 무한 차원으로 확장하는 방법론을 다루며, 이는 RBF 커널을 통해 구성되는 재현 커널 힐베르트 공간 (Reproducing Kernel Hilbert Space, RKHS)을 활용함으로써 효율적으로 달성됩니다.

Section 2: ML Perspective

이 섹션에서는 기본적으로 "Infinite-dimensional feature interaction"[1]의 내용을 주로 담고 있습니다. 그렇기에 논문 리뷰에 가까운 형식입니다. 하지만 저자들이 설명을 생략하였지만 설명이 필요하다 판단되는 경우, 이전 섹션과 마찬가지로 다른 참고 문헌을 통해 보강하는 형식으로 전개됩니다.

Ⅱ.1. Adoption of Infinite in Feature Interaction Space

ML 모델 설계에 왜 무한행렬이 필요할까

Ⅱ.1.1. Overview of Deep Neural Network

Deep Neural Network의 발전 흐름을 먼저 간략하게 알아보자 [1]

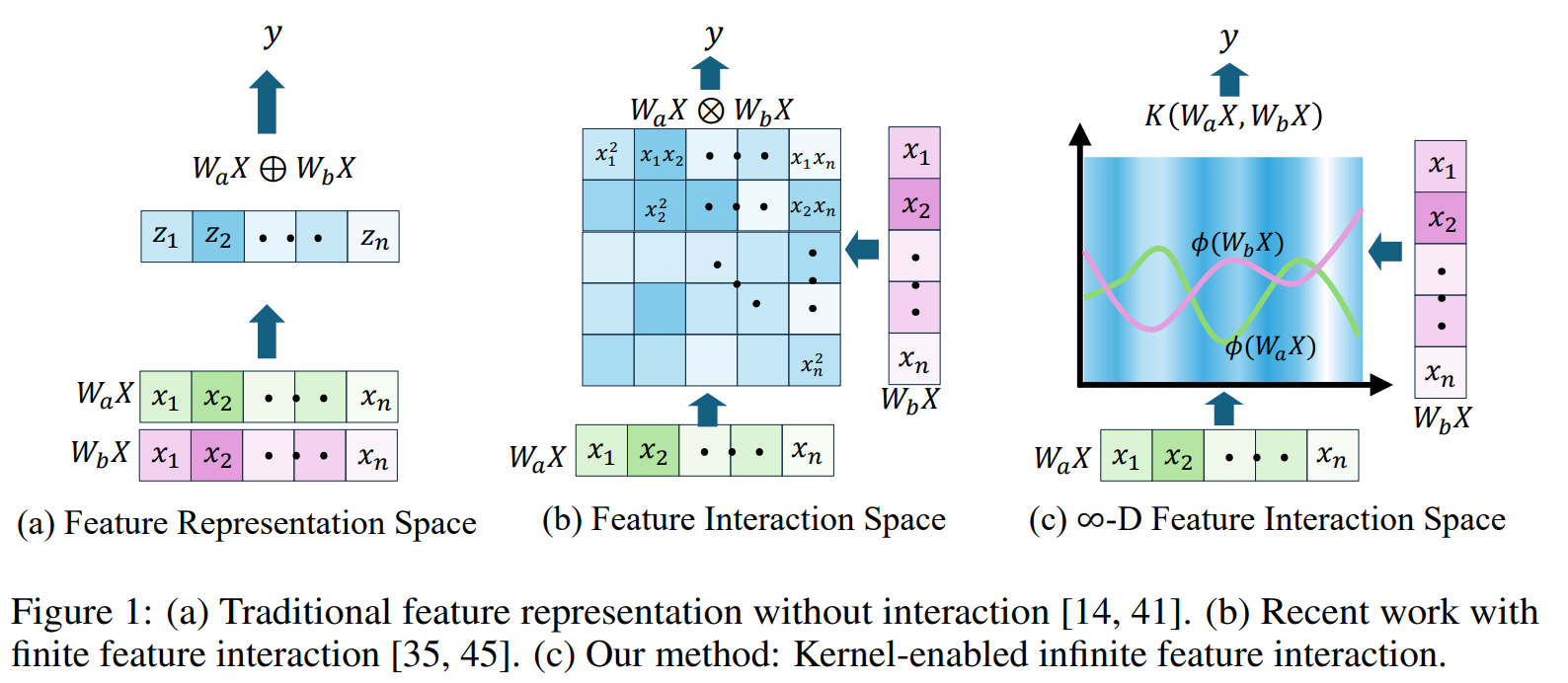
지난 십여년간 심층 신경망 (Deep Neural Network) 아키텍쳐 설계에 대한 패러다임은 몇가지 주요 패러다임들과 함께 큰 변화가 있었습니다.

최초에는 주로 특징 표현 공간 (feature representation space)에 집중하여 이 공간의 차원을 확대하는 방식이나 capacity scaling (e.g. 채널의 폭이나 깊이의 확대) 에 집중한 방식이었습니다. (e.g. Multi-Layer Perceptron (MLP), Convolution Neural Networks (CNN), ResNet)

물론 이런 방식은 지금도 인공지능 분야에 대해 입문한다면 반드시 들어볼 정도로 나름의 의미를 가집니다. 이 방식은 특징 표현 공간에서 $W_ix ⊕ W_jx$ (Direct Sum of vector spaces) 방식의 선형 결합 (linear superposition)을 활용하기에 모델의 채널 폭과 깊이를 확장할 때 모델이 개선되는 것을 확인했다는 점에서 의미가 있습니다 (ConvNext V2). 하지만 이 접근의 가장 큰 한계점은 특징 간 상호작용 (feature-feature interaction)을 고려하지 못한다는 것이었습니다. $^{Fig. \ 1(a)}$

이 한계점을 보완한 패러다임이 바로 상호작용 공간의 확장 (interaction space scaling)으로 관점을 옮기는 것이었습니다. $W_ix ⊗ W_jx$ 방식의 요소별 곱셈 (element-wise multiplication) 을 통한 고차원 특징 상호작용 공간의 활용으로 정보 변환의 개선을 이끌어냈습니다. $^{Fig. \ 1(b)}$

그럼에도 불구하고 요소별 곱셈 방식 또한 여러 한계점이 존재했습니다. 단순한 곱셈 연산 기반의 접근으로 인해 정작 모델이 왜 성능이 좋아지는지에 대해서 이론적으로 설명하거나 정량적으로 분석하기 어렵다는 것이 그 중 하나였습니다. (explainability와 quantifiability의 부족)

개발자가 가장 두려운 순간

물론 이외에도 상호작용의 차수를 점점 높이는 과정에서 차수 $k$ 에 비례하여 계산 비용 역시 선형적으로 증가한다는 문제와 이로 인해 이론적으로는 고차 상호작용 (high-order interactions)이 가능은 하지만 현실적으로는 비효율적이라는 한계점도 존재했습니다.
( ${Fig. \ 1}$ 에서는 $k=2$ 인 이차 상호작용을 고려하고 있습니다.)

그렇기에 이런 한계점들을 극복하기 위해서 "Infinite-dimensional feature interaction"[1] 의 저자들은 한가지 방법을 고안해냅니다. 바로 커널 함수를 활용한 차원의 확장입니다.

Ⅱ.1.2. Introduction of Kernel Method

바로 커널함수의 적용으로 넘어가기 전에 커널함수에 대해 잠시 설명하겠습니다. 이미 커널함수에 대해 아신다면 Ⅱ.2.1. Extension of Feature Interaction Space로 넘어가시면 됩니다.

커널 함수를 알기에 앞서 우리는 왜 커널함수가 필요했을까에 대해 생각해볼 필요가 있습니다.

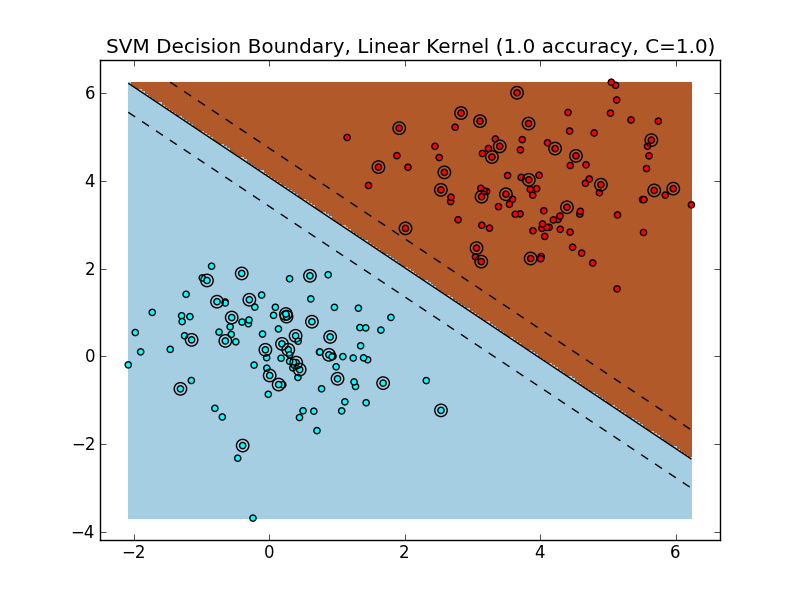
Support Vector Machine (SVM)과 같은 머신러닝에서 활용되는 함수로 주로 언급되는 커널 함수는 주어진 데이터를 고차원으로 사상해주는 함수를 말합니다. 그러면 왜 데이터를 고차원으로 사상해줄 필요가 있었는가? 에 대한 답변은 아래의 이미지 $^{Fig. \ 2, 3}$ 를 보면 쉽게 이해할 수 있습니다.

Figure 2: The Decision Boundary of a Linear SVM on a linearly-separable dataset. The solid line is the boundary. The SVM is trained on 75% of the dataset, and evaluated on the remaining 25%. Circled data points are from the test set [2]

SVM은 기본적으로 데이터의 분류에 있어 $y=0$ 과 $y=1$ 을 가르는 두 클래스 사이의 거리가 가장 넓은, 다시말해 마진이 최대화되는 초평면 (hyperplane)이라는 구분선 (decision boundary)을 찾는 것이 목적입니다. 그런데 실제 데이터는 단순하게 선형 Binary Classification 사례 중에서는 $Fig. 2$ 와 같이 쉽게 선형으로 구분되는 데이터가 있는 반면 $Fig. 3$ (left) 과 같이 선형으로 구분할 수 없는 방식의 데이터도 존재합니다.[2]

Figure 3: (Left) A dataset in $\mathbb{R}^2$ , not linearly separable. (Right) The same dataset transformed by the transformation: $T(~[x_1, x_2]~) = [x_1, x_2, {x_1}^2 + {x_2}^2]$ [2]

그런데 이 데이터를 $Fig. 3$ (right)와 같이 고차원으로 매핑하게 된다면 해당 차원에서는 선형으로 구분짓는 것이 가능해집니다. $^{Fig. 4}$ 그리고 다시 본래 차원에서는 비선형으로 구분할 수 있게 됩니다. Linear SVM임에도 불구하고 말입니다.

Figure 4: (Left) The decision boundary $\vec{w}$ shown to be linear in $\mathbb{R}^3$ . (Right) The decision boundary $\vec{w}$ , when transformed back to $\mathbb{R}^2$ , is nonlinear. [2]

물론 이 방법도 완벽한 방법은 아닙니다. 고차원으로 매핑하는 과정에서 요소별 곱셈 방식과 마찬가지로 계산 비용이 기하급수적으로 증가한다는 동일한 한계점이 있습니다. 이는 아래의 예시에서도 살펴볼 수 있습니다.

Here is a concrete example [2]: the Polynomial Kernel is a kernel often used with SVMs. For a dataset in $\mathbb{R}^2$ , a two-degree polynomial kernel (implicitly) performs the transformation $[x_1, x_2] = [{x_1}^2, {x_2}^2, \sqrt{2} \cdot x_1 \cdot x_2, \sqrt{2 \cdot c} \cdot x_1, \sqrt{2 \cdot c} \cdot x_2, c]$ . This transformation adds three additional dimensions $\mathbb{R}^2$ -> $\mathbb{R}^5$ .

In general, a $d-dimensional$ polynomial kernel maps from $\mathbb{R}^N$ to an ${N+d \choose d}$ -dimensional space [6]. Thus, for datasets with large dimensionality, naively performing such a transformation will quickly become intractable.

그런데 이에 대한 해결책은 SVM이 어떻게 학습하는가에서 찾을 수 있습니다. [3] SVM의 학습 과정에서 중요한건 초평면이고, 이는 아래의 식으로 표현할 수 있고 우리는 $w$ 가 데이터의 선형 결합으로 표현된다는 결론을 얻을 수 있습니다. ( $w=\Sigma_i\alpha_iy_ix_i$ )

$\vec{w}^T\vec{x}+\vec{b}=0$
$\vec{w}$ : 초평면의 법선 벡터 (normal vector)
$\vec{b}$ : 절편 (bias)
$\vec{x}$ : 입력 벡터

따라서 새로운 샘플 $x$ 에 대하여 예측할 때,
( $f(x)=w^T\vec{x}+b=\Sigma_i\alpha_iy_i\langle \vec{x_i}, \vec{x} \rangle$ , where $\vec{x_i}, \vec{x} \in \mathbb{R}^N$ ) 우리가 필요한건 그저 모든 support vector $\vec{x_i}$ 와 입력 벡터 $\vec{x}$ 간의 내적값 뿐입니다.

SVM에서의 Kernel Method의 역할 [2]
: 커널함수 $K(\vec{x_i}, \vec{x_j})$ 를 활용하면 추가 메모리 사용 없이 암묵적으로 데이터 셋을 고차원 $\mathbb{R}^M$ 로 변환할 수 있습니다.

따라서 우리는 SVM의 비선형 결정 경계를 단순히 커널함수를 활용한 내적값 연산으로 구할 수 있게 되는 것입니다.

Kernel Method에서 활용되는 주요 커널들

아래의 세가지 함수에 대하여 $\vec{x_i}, \vec{x_j} \in \mathbb{R}^N$ 는 데이터셋 $X$ 에서의 행 벡터임을 가정합니다.

다항식 커널 (Polynomial Kernel): $(\gamma \cdot \langle \vec{x_i} , \vec{x_j} \rangle + r)^d$

방사 기저 함수 커널 || 가우시안 커널 (Gaussian Radial Basis Function (RBF) Kernel): $exp(-\gamma \cdot \lvert \vec{x_i} - \vec{x_j} \rvert ^2)$ , where $\gamma > 0$
⇾ 이 가우시안 커널이 바로 InfiNet에서 활용하는 커널 함수입니다.

시그모이드 커널 (Sigmoid Kernel): $tanh(\langle \vec{x_i}, \vec{x_j} \rangle + r)$

Ⅱ.2. Application of InfiNet

Ⅱ.2.1. Extension of Feature Interaction Space

그렇다면 어떻게 차원을 무한차원으로 확장하면서 비용측면에서 효율적으로 할 수 있을까?

How can we efficiently extend interactions to an infinite-dimensional space?

다시 맨 처음 봤던 이미지로 돌아와봅시다.

기존의 특징 표현 공간이 $V = \text{Span}(x_1, x_2, \cdots, x_n)$ 이라는 $n$ 차원 벡터 공간이었다면, 요소별 곱셈( $\otimes$ )을 사용하면 암묵적으로 이차 상호작용 공간 $Q = \text{Span}(x_1^2, x_1x_2, \cdots, x_n^2)$ 이 구성됩니다. 이 이차 상호작용 공간 $Q$ 의 차원은 $n(n+1)/2$ 로, 기존의 $n$ 차원에서 차원이 확장됩니다.

이러한 일관된 차원 확장의 관점에서 고차원 특징 표현공간을 활용하기 위해 요소별 곰셈 대신 커널 함수를 활용하게 되는 것입니다. 그리고 이때 커널함수에서 활용되는 고차원 특징 표현공간으로 재현 커널 힐베르트 공간 (Reproducing Kernel Hilbert Space, RKHS)을 채택합니다. $RKHS$ 는 매우 적은 비용으로 특징 상호작용 공간을 확장할 수 있게 하는데, $RKHS$ 에 대해서 깊이 다룰 경우 글이 굉장히 길어지고 어려워지기에 우선은 $RKHS$ 와 커널 함수의 관계성에 대해 다루고 넘어가고자 합니다.

$RKHS$ 은 커널 함수 $K(\cdot, \cdot)$ 에 의해 구성되는 초고차원 공간입니다. 특징 $s$ 와 $t$ 사이의 상호작용은 명시적인 매핑 $\Phi(\cdot)$ 을 통해 RKHS에서의 내적 $\langle \Phi(s), \Phi(t) \rangle$ 으로 정의되는데, 실제 계산은 저차원 공간에서 커널 함수 $K(s, t)$ 를 평가하는 것으로 대체됩니다. $K(s, t) = \langle \Phi(s), \Phi(t) \rangle$ (RKHS 내적) 그리고 이것이 우리가 $RKHS$ 를 통해 이루려는 저차원 공간에서의 고차원 공간 활용입니다.

그리고 이런 $RKHS$ 를 활용하기 위해 필요한 커널함수가 바로 앞서 언급된 가우시안 커널 함수 (RBF Kernel)입니다. 가우시안 커널 함수의 수학적 구조 로 인해 두 특징 벡터의 내적을 계산할 때, 암묵적으로 이 벡터들을 모든 차수의 상호작용 항을 기저로 갖는 무한 차원 힐베르트 공간으로 매핑하게 되고, 이때 암묵적으로 정의되는 무한 차원 공간이 바로 재현 커널 힐베르트 공간(RKHS)이 됩니다.

가우시안 커널 함수 (RBF Kernel)의 수학적 구조?
간단하게 원리만 언급하자면, 가우시안 커널 함수의 전개식은 $Krbf(s, t) = exp(-1/2 * ||s-t||²)$ 이고, 이를 전개하면 $exp(-1/2 * ||s||² - 1/2 * ||t||²)$ 와 $exp(sᵀt)$ 항의 곱으로 분리되는데 이때 $exp(sᵀt)$ 항의 테일러 급수 (Taylor series) 전개가 무한 차원 공간의 핵심을 이룹니다.

결론적으로 모든 차수의 단항식 상호작용 항 { $1, \ xᵢ,\ xᵢxⱼ,\ xᵢxⱼxₖ,\ ...$ }에 해당하는 기저(basis)를 포함하는 공간으로 벡터를 매핑하게 됩니다. (⇾ 무한 차원 힐베르트 공간(Hilbert Space)

어렵다 느끼시더라도 괜찮습니다. 단지 여기서는 RBF Kernel을 통해 무한 차원을 활용할 수 있다, 그리고 그 차원이 바로 RKHS다 정도만 이해하시면 됩니다.

따라서 신경망의 특정 연산을 이 커널 함수로 대체하면, 모델은 매우 적은 계산 비용으로 이 무한 차원 공간상에서의 내적 연산을 수행할 수 있게 되어, 데이터에 내재된 매우 복잡하고 비선형적인 특징 간의 상관관계를 효율적으로 모델링할 수 있게 됩니다.

Figure 5 :Comparison of simple representation, finite interaction, and infinite-dimensional interaction. The ? circle in Demo Block is chosen from element-wiseAdd,element-wiseMul., or RBF kernel. [1]

${Fig. \ 5}$ 에서 볼 수 있듯이 Canadian Institute For Advanced Research (CIFAR10) 데이터셋을 활용한 이미지 분류에 RBF Kernel을 활용해보면 유의미하게 정확도가 증가함을 확인할 수 있습니다.

Ⅱ.2.2. Application of InfiNet

Figure 6: Overview of InfiNet.
(a) Four-stage hierarchical InfiNet design. (b)InfiBlock Design [1]

InfiNet의 기본 구성 요소는 InfiBlock이며, 기존의 합산( $\oplus$ )이나 곱셈( $\otimes$ )을 RBF 커널 기반의 상호작용으로 대체합니다.

InfiBlock 구조:
LayerNorm을 시작으로, 특징을 두 그룹의 분리된 표현으로 변환하고, 깊이 방향 합성곱 연삽(depth-width convolution)을 통해 특징 벡터를 얻습니다.

- 커널 적용: 이 두 그룹의 특징 벡터( $\vec{Z}^l_a, \vec{Z}^l_b$ )는 하이퍼파라미터가 없는 RBF 커널 $\text{K}_{rbf} (\vec{Z}^l_a, \vec{Z}^l_b) = \exp(-\frac{1}{2} | \vec{Z}^l_a - \vec{Z}^l_b |^2_2)$ 에 입력되어 상호작용을 계산합니다.

이때 이 연산이 명시적인 고차원 계산 없이 무한 차원 특징 상호작용 공간을 생성하는 역할을 수행하게 됩니다.

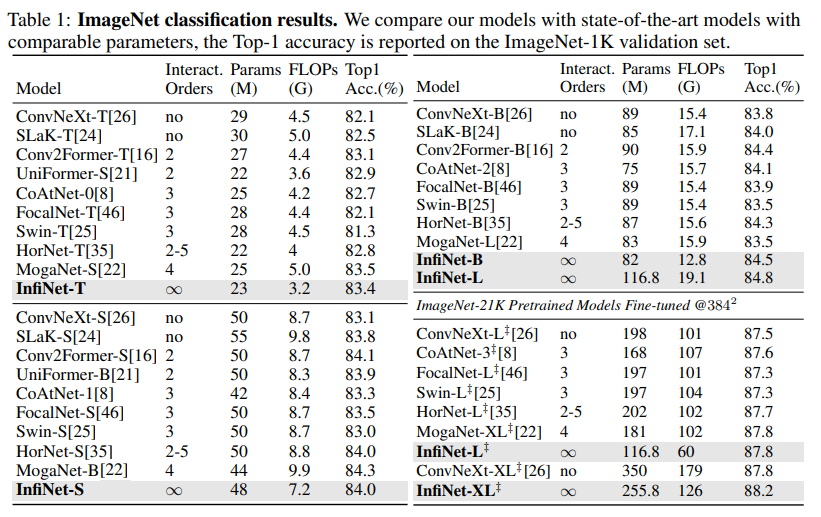
$Table \ 1$ [1]에서는 실제 ImageNet Classification 분류 성능을 다른 이미지 분류 모델과 함께 비교한 표입니다. 이 표에서 역시 InfiNet 기반의 모델은 준수한 퍼포먼스를 보여주고 있습니다.

FLoating point Operations Per Second (FLOPs)는 상대적으로 낮고 (높은 정확도)
모델 크기(T→XL)가 커질수록 성능이 안정적으로 증가하며, 대규모 학습(ImageNet-21K fine-tuning)에서도 88.2%로 최고 수준을 보여주고 있습니다.

이 밖에도 "Infinite-dimensional feature interaction"[1] 에서는 각기 다른 이미지 분류 및 객체 탐지 데이터셋에서의 InfiNet의 성능을 시험해보았고, 좋은 성능을 보여주었습니다.

Ⅱ.2.3. Conclusion

물론 이번 블로그 글에서 언급된 InfiNet 모델은 아직 기초적인 이미지 분야만에서의 검증이고, 다른 분야에 대해서는 아직 검증되지 않았습니다. 그렇기에 더 다양한 조건에서 검증되어야 합니다.

하지만 InfiNet은 신경망 아키텍처의 성능 향상 원동력을 특징 상호작용 공간의 차원 확장이라는 통합된 이론적 관점에서 재해석하고, 이 차원을 궁극적인 목표인 무한 차원으로 효율적으로 확장하는 방법론의 가능성을 제시한 시도였다고 생각합니다.

References

1. Xu, C., Yu, F., Li, M., Zheng, Z., Xu, Z., Xiong, J., & Chen, X. (2024). Infinite-dimensional feature interaction. Paper presented at the 38th Conference on Neural Information Processing Systems (NeurIPS 2024). https://arxiv.org/abs/2405.13972

2. Kim, E. (n.d.). Everything you wanted to know about the Kernel Trick. Eric-Kim. https://www.eric-kim.net/eric-kim-net/posts/1/kernel_trick.html

3. Jordan, Michael I., and Romain Thibaux. "The Kernel Trick." Lecture Notes. 2004. Web. 5 Jan. 2013. http://www.cs.berkeley.edu/~jordan/courses/281B-spring04/lectures/lec3.pdf

같이 보면 좋은 블로그 글/유튜브

서포트 벡터 머신(SVM)의 사용자로서 꼭 알아야할 것들 - 매개변수 C와 gamma
: SVM에 대한 전반적인 지식을 습득하기 좋은 블로그 글입니다.
SVM with polynomial kernel visualization
: SVM에서 Kernel 함수의 적용에 대한 기초적인 글입니다.

마무리하며

이번 Research Note 시리즈의 시작을 개인적인 호기심에서 출발한 무한 행렬의 활용으로 열어보았는데, 처음 쓰는 전문적 글이기도 하고 아직 완전히 숙달된 분야가 아닌지라 이래저래 군더더기 많은 글이 작성된 것 같습니다. 또한 글의 공간적인 한계로 설명하지 못한 개념도 많기에 추후 조금씩 보강할 예정입니다.

앞으로도 Research Note 시리즈는 이런 식으로 저의 학부 생활 동안 가졌던 의문점에 대해 같이 공유하고 혹시나 저와 같은 생각을 해본 사람이 있다면 유용하게 활용되길 바라며 작성할 것 같습니다.

긴 글 읽어주셔서 감사합니다. 이 글에 대해 의견이 있거나 추가적으로 궁금한 사항이 있다면 편하게 댓글로 남겨주세요.