Abstract

Structured pruning은 더 작고 빠른 LLM을 만들기 위한 경량화 방법이다.

기존 Pruning 방법들은 대부분 Backpropagation을 필요로 하기 때문에, Backpropagation을 위해 gradient 계산 비용과 메모리 사용량이 크게 증가한다는 단점이 존재한다.

본 논문에서는 새로운 Structured pruning 기법을 소개한다.

• Bonsai

  Gradient를 사용하지 않고, 오직 forward pass만을 이용하여 pruning을 수행하여 메모리와 계산 비용을 획기적으로 줄이면서 높은 수준의 pruning 성능을 달성한다.

Perturbation 기반 pruning을 통해 다양한 하드웨어 환경에서 대규모 모델을 효율적으로 compress할 수 있게 한다.

기존의 Structured pruning 기법들과 다르게 Bonsai는 더 적은 자원으로 더 나은 compression 성능을 보이며 semi-structured pruning보다 2배 빠른 모델을 생성한다.

Structured pruning

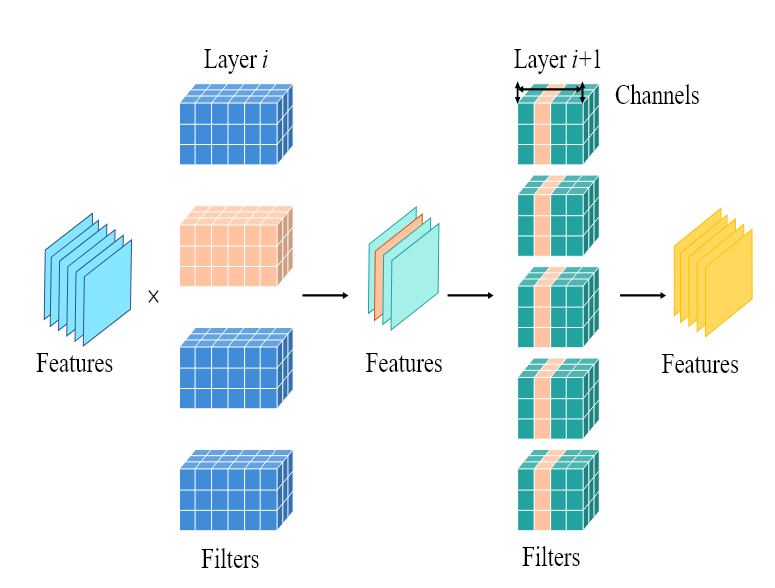
모델의 전체 구조 단위를 제거하는 방식
예를 들어, 전체 뉴런, 채널, layer, filter, Attention head 등을 모듈 전체를 제거하는 방식이다.

제거된 구조 단위가 크고 규칙직이기 때문에 실제 하드웨어에서의 계산에서 빠지기 때문에 속도 향상과 메모리 절감이 가능하지만,
모델의 구조 자체가 변경되기 때문에 잘못 제거 시에 성능이 급락할 수 있기 때문에 재학습이나 재배치가 필요하다

Semi-structured pruning

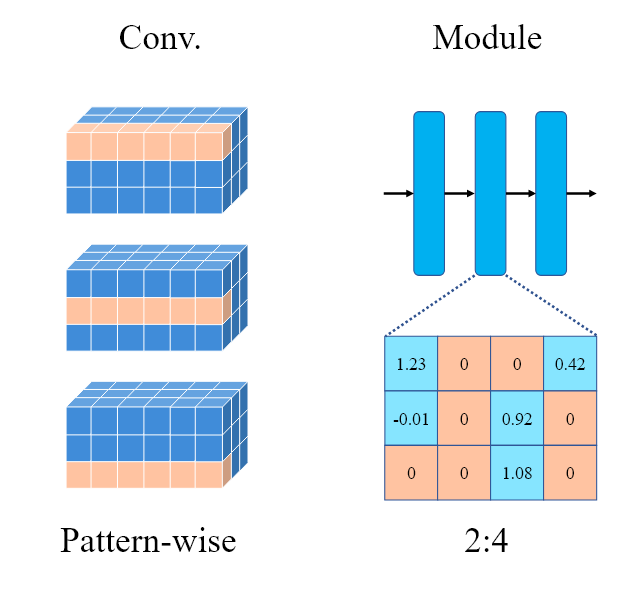
Structured와 Unstructured pruning의 중간 형태로, 작은 block이나 pattern 단위로 부분적으로 가중치를 제거하면서도, 일정한 제거 규칙을 유지한다.

대표적으로 2:4 pruning은 각 layer의 weight 행렬은 크기 4로 묶어서, 그룹 내 가중치에 특정 기준으로 중요도 점수를 매겨 상위 2개의 가중치만 남기고 masking하는 방식이다.

Unstructured 형태이지 Structured와 같은 규칙성을 갖기 때문에 Structured보다 높은 sparsity를 달성할 수 있다.

모든 block이 동일한 N:M 패턴을 가지므로 하드웨어 가속시에서 연산 라이브러리를 효율적으로 설계할 수 있다.

Unstructured pruning

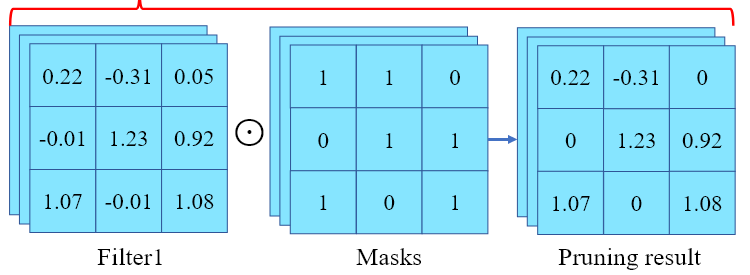
Unstructured pruning은 신경망의 개별 파라미터 단위로 중요도가 낮은 가중치를 masking하여 0으로 만드는 방식으로, 어느 위치든 상관 없이 전체 파라미터 중 중요도 기준에 따라 임계값 이하의 weight를 제거한다.

동일한 sparsity에서 Structured pruning보다 더 많은 가중치를 제거할 수 있어, 모델 크기를 크게 줄이면서도 모델의 구조를 유지할 수 있다.

제거할 위치를 개별적으로 선택하기 때문에, 모델의 중요한 연결은 그대로 남기고 불필요한 연결만 정밀하게 제거할 수 있지만,
파라미터가 불규칙적으로 분포해 있기 때문에, 벡터/행렬 사속기에 최적화된 연산 스케줄링이 어렵고 sparse matrix 연산을 빠르게 처리하기 위한 특수 라이브러리나 하드웨어가 필요하다.

Intruduction

LLM이 지속적으로 커지면서, 이를 실행하고 배포하는 데 필요한 연산 자원도 급격하게 늘어나고 있다.
이런 모델의 크기와 연산 부담을 줄이기 위해 Structured pruning이 사용되어 왔는데, 기존의 Structured pruning은 Gradient를 계산하는 backpropagation에 의존하기 때문에 메모리와 연산 비용이 크게 증가한다.

Forward pass 도중 각 layer마다 입력/출력 값을 저장해 두어야 Backpropagation에서 그 값을 이용하여 gradient를 계산할 수 있는데, 이 저장된 Activation 값이 모델 크기와 동일하거나 그 이상의 메모리를 차지하기 때문에 메모리 사용량이 최소 2배로 뛸 수 밖에 없다

Backpropagation은 Forward pass에 비해 최소 2배 이상의 메모리를 소모하며, Optimizer인 AdamW를 이용한 Optimizing(Gradient descent 파라미터 업데이트)은 3배 이상의 메모리를 요구한다.

결과적으로 Forward pass의 Activation 메모리/연산량과 Optimizer의 메모리/연산량이 합쳐져서, backpropagation을 필요로 하는 structured pruning은 메모리 사용량과 연산량이 모두 크게 증가하게 된다.

이러한 한계를 해결하기 위해, 본 논문에서는 Bonsai라는 새로운 Structured pruning 기법을 제안한다.

Bonsai는 전체 pruning 과정을 오직 Forward pass만으로 수행하여, Backpropagation으로 인한 메모리/연산 부담을 제거함으로써 기존 방법으로는 불가능했던 대형 모델의 pruning을 가능하게 한다.

Bonsai는 Structured/Unstructured의 기존 방법들보다 더 우수한 성능을 보여준다.

Bonsai에서는 Structured pruning을 위해 모듈의 중요도를 측정할 때, Gradient를 계산하지 않기 때문에 Forward pass기반의 Perturbative라는 evaluation을 도입하여 모듈의 중요도를 측정한다.

Perturbative

각 모듈을 삭제한 모델을 하나씩 만들어, 그 성능 저하를 측정하여 모듈에 대한 중요도를 측정하는 방법

• 모델에 1000개의 모듈이 있으면, 1000번의 Forward pass가 필요한데, LLM 수준에서는 비용이 너무 크다

Bonsai의 아이디어

1. Undetermined regression 문제로의 재구성

1. 랜덤 sub-model 샘플링

   여러 모듈을 한꺼번에 랜덤하게 지운 sub model을 적은 개수로만 만들어서 그 성능을 측정한다.

2. Regression 문제로 변환

   이 적은 개수의 sub model의 성능 저하 결과를 어떤 모듈이 얼마나 중요했는지를 예측하기 위한 데이터로 삼는다.

3. Underdetermined 문제

   관측치(랜덤 sub model 개수) < 전체 모듈 개수 일 때도, Regression 기법을 사용하면 최소한의 sub model 평가로도 중요도를 합리적으로 추정할 수 있다

2. 사전 정보 활용

1. 먼저 Unstructured pruning 기법을 활용해 절댓값이 작은 weight들을 미리 파악한다.

   이 절댓값 기반 중요도는 대략 "이 모듈은 덜 중요할 것 같다"는 단서를 준다.

2. 우선 순위 샘플링

   sun model을 만들 때, "덜 중요할 것 같은" 모듈은 더 자주 뽑아서 지워보고, "아마 중요할 것 같은" 모듈은 조금 덜 자주 뽑는다.

3. Global 모듈 제거

이전의 Gradient-free 방법들은 1개 layer씩 그 안에서만 중요도를 계산해서 제거하는 방법을 반복했는데, 이러면 초기 layer에서 너무 많이 잘라버려서 뒷부분 layer를 제거할 기회가 사라지는 등의 전체 모델 균형이 깨질 수 있다.

1. 모델 전체를 한 번에 본다.

   Regression을 통해 추정된 중요도를 전부 모아서 어떤 layer든 전체 중요도 기준으로 낮은 모듈부터 제거한다.

Methodology

2.1 Background on Pruning, Problem Definition and Notation Setup

파라미터 $\theta \in \R^D$로 정의된 LLM($M_\theta$)과, 이 모델이 특정 task에서 얼마나 잘 동작하는지를 측정하는 함수 $U$(Accuracy, Perplexity..등)가 주어졌다고 가정한다.

메모리 제약 하에서 $M_\theta$의 Inference가 가능하도록 크기는 더 작고 속도는 더 빠르면서도 $U$관점에서 성능이 우수한 모델을 얻기 위해 pruning을 적용한다.

Structured pruning은 모델을 이루는 작은 단위들을 모듈 단위로 제거한다는 의미이다.

1. $M_\theta$(LLM)를 $m=\{m_1,...,m_N\}$이라는 $N$개의 모듈 집합으로 보고

2. 각 모듈 $m_i$는 $s_i$개의 파라미터를 포함하여, $\sum_is_i=D$가 되도록 정의한다.

   • $s_i$는 모듈의 파라미터 수
   • $D$는 모델 전체 파라미터 수

3. sub model $\tilde{\mathbf{m}} \subseteq \mathbf{m}$(sub model을 구성할 모듈$m_i$의 집합)을 선택하면 $\tilde{\mathbf{m}}$에 포함되지 않은 모듈을 제거하여 새로운 모델 $M_{|\tilde{\mathbf{m}}|}$을 생성한다.

4. 희소도(Sparsity) 제약

• 목표 희소도 ($p$)가 주어지면, 전체 파라미터의 $p$비율만큼 제거하면서도 $U$를 최대화하는 조합 최적화로 표현된다.

  $\mathbf{m}^* = \arg\max_{\tilde{\mathbf{m}} \in \mathcal{F}_p}U\left(M_{|\tilde{\mathbf{m}}|}\right)$

• 이 조건을 만족하는 서브모델의 집합:

  $\mathcal{F}_p = \left\{ \tilde{\mathbf{m}} \subseteq \mathbf{m} \;\middle|\; \sum_{m_j \in \tilde{\mathbf{m}}} s_j \le (1 - p) D \right\}$

기존의 Structured pruning 기법들은 제거할 모듈을 구할 때 gradient-based로 풀고자 하지만,
메모리 제약으로 인해 Backpropagation(gradient 계산)이 불가능한 환경에서는 이러한 방법을 사용할 수 없다.

2.2 Estimating module relevance with only forward passes

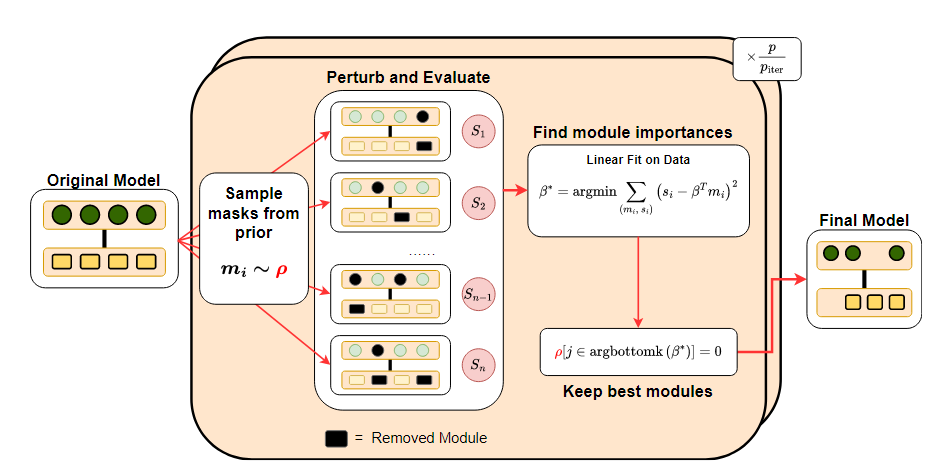
메모리 부담이 너무 카서 Forward pass만 가능한 모델을 pruning할 때,

$\mathbf{m}^* = \arg\max_{\tilde{\mathbf{m}} \in \mathcal{F}_p}U\left(M_{|\tilde{\mathbf{m}}|}\right)$

이 수식을 gradient 기반이 아니라 평가 함수 $U$를 기반으로 최적의 pruned model을 찾아야 한다.

하지만, 모델의 크기가 큰 LLM에서 고려할 수 있는 모든 sub model의 집합 $\mathcal{F}_p$를 전부 탐색하는 것은 조합의 크기가 너무 커서 불가능하다.

이를 해결하기 위해, 훨씬 작은 수 $n \ll |\mathcal{F}_p|$번의 평가만 수행하여, 모델 $M$의 각 모듈이 평가 함수 $U$에 기여하는 정도를 추정할 데이터를 모은다.

Sampling을 통해 n개의 sub model을 만들고, 각 sub model에 대해
회귀식을 풀어 각 모듈에 대한 중요도 점수 $\beta_i$를 구한다.

모델 내 $N$개의 모듈($\beta_i$)에 대한 중요도 점수를 sampling을 해 $\beta=\{\beta_i\}^N_{i=1}$로 추정했다고 하면

이 식에 대한 근사 해는 다음과 같다.

$\mathbf{m}^* \approx \mathbf{m^{approx}= \arg\max_{\tilde{\mathbf{m}} \in \mathcal{F}_p}\sum_{j \in \tilde{\mathbf{m}}}\beta_j}$

$\arg\max_{\tilde{\mathbf{m}} \in \mathcal{F}_p}\sum_{j \in \tilde{\mathbf{m}}}\beta_j$ : 모든 sub model(모듈 집합) $\mathcal{F}_p$ 내에서, 모듈(j) 중요도 점수 ($\beta_j$)의 합($\sum_{j \in \tilde{\mathbf{m}}}\beta_j$)이 가장 큰 sub model $\tilde{m}$을 찾아 근사 해로 선택한다

• $\beta_j$ : sub model 내 모듈 j가 평가 함수 $U$에 기여하는 정도를 나타내는 수
• $\beta_j$가 클수록 꼭 남겨야 할 중요 모듈이므로, 가장 중요한 모듈들의 집합을 만들려면, $\beta$의 합이 최대인 집합을 찾으면 된다

하지만 $\mathcal{F}_p$의 크기는 지수적으로 크기 때문에 모든 sub model에 대해 중요도 점수의 합을 구하는 건 불가능하다

$\mathcal{F}_p$ 내에서, 중요도 점수의 합($\sum\beta_j$)이 가장 커지는 sub model을 찾기 위해 Greedy search를 이용한다.

• Samplling을 통해 구한 모델 내 모듈 중요도 점수 ($\beta_j$)를 내림차순 정렬하여 sparsity 제약을 만족하는 한에서 차례대로 중요도가 높은 모듈부터 선택하여 sub model의 근사 해를 만든다.

모듈별 중요도 점수 $\beta_i$

1. 데이터 수집

1. 서브 모델 생성

• 전체 모듈 집합 $m$에서, $|\mathcal{F}_p|$ 중 아주 작은 수 $n \ll |\mathcal{F}_p|$개의 부분 집합 $\tilde{m}_1,..., \tilde{m}_n$을 샘플링한다

2. 성능 측정

• 각 서브 모델 모듈 집합 $\tilde{m}_k$에 대해 $\tilde{m}_k$에 속하지 않는 모듈들을 제거한 가상의 모델 $M_{|\tilde{m}_k|}$을 Forward pass만 이용해 task를 실행하여 성능 $U_k=U(M_{|\tilde{m}_k|})$을 기록한다.

3. 데이터셋 구성
   n개의 모듈 부분 집합에 대해 모두 가상의 모델을 만들어 성능을 측정해 기록하여 데이터셋을 구성한다

   $\mathcal{D}=\{(\tilde{m}_k, U_k)\}^n_{k=1}$

2. 이진 마스크 $\alpha_{\tilde{m}}$

각 sub model에 대해 이진 마스크로 표현한다

$(\alpha_{\tilde{\mathbf{m}}_k})_i =\begin{cases}1, & i \in \tilde{\mathbf{m}}_k(모듈 m_i가 sub model에 포함됨(남김),\\0, & 모듈 m_i가 sub model에 포함되지 않음(제거됨)\end{cases}$

예) $N$ = 5일 때, $\tilde{m}_k = \{m_1, m_3, m_5\}$이면 $\alpha_{\tilde{\mathbf{m}}_k} = [1,0,1,0,1]^T$

3. 회귀 문제

$\hat\beta= \arg\min_{\beta\in\mathbb{R}^N}\frac{1}{n}\sum_{k=1}^n \bigl(U_k - \beta^T \alpha_{\tilde{\mathbf{m}}_k}\bigr)^2 \;+\;\gamma\,\|\beta\|$

1. n개의 sub model들을 평가해 성능 $U_k$와 이진 마스크 $\alpha_k$를 얻음
2. $\beta$를 찾으면 $\beta^T \alpha_k$와 $U_k$가 근사해지겠지 라는 가정하에 회귀
3. 회귀를 통해 각 모듈 i에 대해 얼마나 성능에 기여하는지를 나타내는 $\hat\beta_i$를 획득한다. 이후, 이 값으로 greedy하게 선택하여 근사해를 함

• (A) 평균 제곱 오차($\frac{1}{n}\sum_{k=1}^n \bigl(U_k - \beta^T \alpha_{\tilde{\mathbf{m}}_k}\bigr)^2$)

  각 sub model의 관측 값 $U_k$와 예측 값 $\beta^T \alpha_k$ 차이의 제곱을 평균

  예시)
  
  

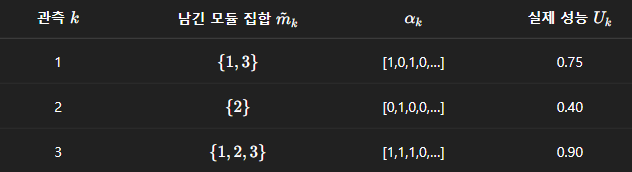
  • 관측값 (0.75, 0.4, 0.9)와 예측 값 ($\beta_1+\beta_3$, $\beta_2$, $\beta_1+\beta_2+\beta_3$)의 차이를 제곱해 더한 뒤 평균을 낸다
  • 이 값이 작을수록 선형 모델이 관측 데이터를 잘 따라간다는 뜻

• (B) 정규화($\gamma\,\|\beta\|$)

  Ridge 회귀를 사용하며, $\beta$값이 너무 커지지 않게 과적합을 방지한다.

  • 정규화 없이 풀면 실제로는 관측치의 개수가 모듈의 개수보다 훨씬 적게되어 단순 최소 제곱만 사용하게 되면 매우 불안정하거나 해가 무수히 많아진다

Ridge 회귀를 통해 얻은 $\hat\beta$를 이용하여 $m^{approx}$를 구함

2.3 Selecting sub-models for evaluation

그렇다면, 중요한 은 $n \ll |\mathcal{F}_p|$개의 sub model을 어떻게 골라 평가에 사용할지(Sampling)을 결정하는 일이다.

하지만, 단순한 방법인 Uniform sampling은 최적이 아님이 보여진다.

Uniform sampling : 모든 모듈이 뽑힐 확률이 균등

어떤 모듈 $m_i$가 성능 지표 $U$에서 중요하다 해도, 관측치가 전체 모듈 개수보다 작기 때문에(n<N) 해당 모듈이 sub model 목록에 단 한 번도 포함되지 않을 수 있다.

만약 모듈 $m_i$가 뽑힌 n개의 sub model 목록에서 전부 빠진 모듈이 되면, 회귀를 통해 얻는 $\hat\beta_i=0$이 되어버리기에, $m^{approx}$는 최적의 sub model이 아니게 될 것이다.

따라서, 정보에 기반한 Sampling이 필요하다.

각 모듈 $m_i$에 대해, sub model sampling시에 그 모듈이 포함될 확률을 prior score(각 모듈이 얼마나 유용할지)$p_i$에 비례하도록 설정한다.

$p_i$는 pruning 논문들에서 제안된 여러 지표(weight magnitude, activation magnitude) 등으로 정의할 수 있다.

예를 들어, activation magnitude를 prior로 삼는다면, 여러 입력 샘플 $x_b$에 대해 각 layer 출력의 절댓값을 평균 내어 prior로 둔다.

$\hat\alpha_i=\frac{1}{B}\sum^B_{b=1}|\sigma(W^T_{[i,:]}x_b)|$

• $\frac{1}{B}\sum^B_{b=1}$ : B개의 입력 샘플에 대한 평균
• $|\sigma(W^T_{[i,:]}x_b)|$ : Layer별 활성화 값

이렇게 하면 성능이 높을 것 같은 모듈이 샘플링될 확률이 커지므로, $\beta$ 추정의 정확도가 올라간다

$p_i$계산은 원본 모델 $M_{\theta}$에 대해 한 번만 forward해도 가능하기 때문에, 메모리 효율성도 유지된다.

효율을 더 높이기 위해, 각 Layer당 prior 순위로 가장 하위 2p 비율의 모듈만 prune 대상으로 삼고, 나머지 상위 1-2p 비율은 고정해 두는 기법을 쓴다.

즉, p=0.2라면, 전체 모듈의 20%를 pruning하는 것인데 하위 40% 중에서 어떤 20%를 pruning할지에 대한 조합만 sampling하여 sub model을 만들어 회귀에 사용

2.4 Iterated Pruning

한 번에 파라미터를 제거하면, pruning 후에 모델 성능이 크게 떨어지거나, 잘못된 모듈을 제거할 위험이 크다.

작은 비율 $p_{iter}$씩 여러 단계로 나눠서 제거하면, 각 단계마다 prior와 $\beta$를 재추정하며 더 안정적인 pruning이 가능하다.

이에 따라, 목표 sparsity보다 작은 1회당 pruning 비율 $p_{iter}<p$를 정의하고 $iter=p/p_{iter}$단계만큼 반복 수행한다.

각 단계마다 평가할 sub model 개수도 $n_{iter}=n/iter$개로 나누어, 한 번에 $n_{iter}$개의 sub model을 탐색한다.

추정된 $\beta^*$를 내림차순 정렬한 뒤, 가장 작은 $\beta_i$들만 골라 pruning한다.

iter만큼 반복하면서 한 단계당 소량씩 pruning을 진행하며, 반복이 끝나면, 목표 sparsity를 만족하는 최종 pruned model이 완성된다.

3. Experimental Details and Main Results

• 실험 대상 및 환경

  약 7B 파라미터급 LLM(LLaMA-1/2-7B, Phi-2 3B)을 대상으로, Attention head와 MLP 차원을 모듈 단위로 Structured pruning

3.1 Bonsai is competitive with other forward pass-only, structured pruning methods

Forward-only structured pruning과 비교

• 대상 : LLaMA-2-7B
• Sparsity : 50%
• Dataset : Wikitext-2, C4
  

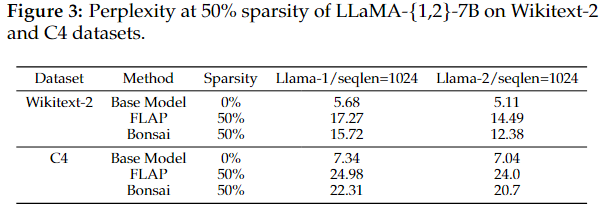
FLAP보다 더 낮은 Perplexity를 달성

Perplexity : 모델이 테스트 데이터 분포를 얼마나 “혼란스러워” 하는지 나타내는 척도

• PPL이 낮으면 모델이 거의 완벽하게 다음 결과를 예측
• PPL이 높으면 모델이 예측에 많은 혼란을 겪고, 가능한 결과 후보가 많음

3.2 Introducing Post-Pruning Adaptation (PPA)

Pruning 후, student 모델을 fine-tuning하거나 LoRA+distillation을 적용해 성능을 회복

3.2.1 Bonsai is competitive with semi-structured pruning methods

Semi-structured Wanda (2:4)와 비교

• 대상 : LLaMA-2-7B
• Sparsity : 50%
• Dataset : Wikitext-2
  
  Wanda는 PPA 시 속도가 크게 저하되지만, Bonsai는 속도를 유지하면서 PPL(Perplexity)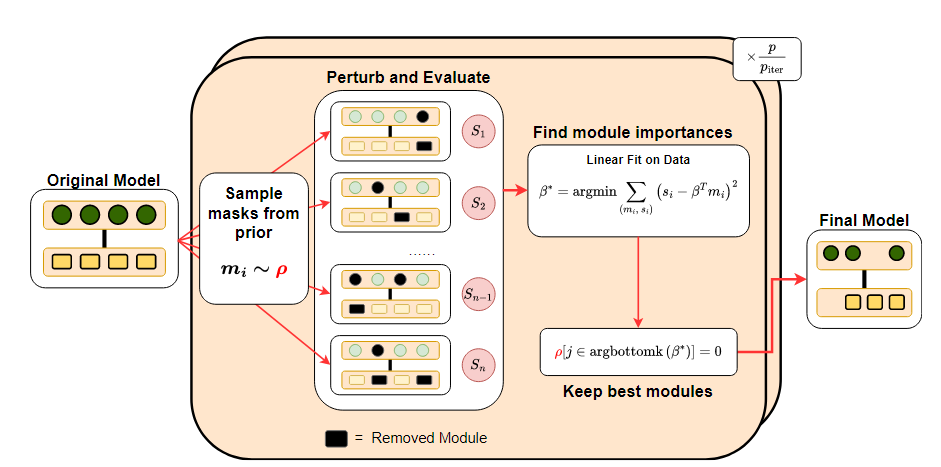
  
  도 유사수준으로 회복
  

3.2.2 Bonsai is competitive with gradient based structured pruning

Gradient-based Structured Pruning 비교

• 대상 : LLaMA-1-7B
• Sparsity : 50%
• Dataset : Wikitext-2 + BoolQ, HellaSwag, WinoGrande, ARC-e, ARC-c
  

  gradient 없이 forward만으로도, 기존 gradient-based 기법들을 능가

3.2.3 Bonsai can produce compressed models with strong zero-shot abilities

Zero-shot 성능을 PPA가 아닌 fine-tuning으로 비교

• 대상 : Phi-2 (3B)
• Sparsity : 35%
• Dataset : C4 100K

  fine-tuning을 통해, 작지만 경쟁력 있는 제로-/few-shot 성능 확보