[논문리뷰] Extending Stein’s unbiased risk estimator to train deep denoisers with correlated pairs of noisy images
논문 리뷰 + 구현
안녕하세요. 밍기뉴와제제입니다. 이번에 리뷰할 논문은 Extending Stein’s unbiased risk estimator to train deep denoisers with correlated pairs of noisy images, 줄여서 eSURE입니다.
eSURE은 이미지 디노이징(denoising)을 구현한 네트워크를 비지도 학습시킬 때 사용하는 함수입니다. 비지도학습에 대해 자세히 알아볼 기회가 없었는데 이번 논문을 공부하며 비지도학습을 공부해보는 기회를 가질 수 있어 좋았습니다.
그러면 지금부터 리뷰를 시작하도록 하겠습니다.
1. Introduction
DNN(Deep neural network, 이하 네트워크)은 이미지 디노이징에서도 유용히 쓰이고 있습니다. DNN을 이용해 실제 노이즈는 물론 가상으로 생성된 Gaussian Noise(이하 가우시안 노이즈)를 제거할 수 있다는 사실을 보여줬죠
랜덤한 값을 가지는 노이즈(확률 변수)들을 모두 합치면 가우시안 분포가 나옵니다. 그래서 노이즈를 가우시안 분포라 가정하고 이를 제거하기 위한 시스템을 설계하면 노이즈를 제거하는 시스템을 만들 수 있습니다.
https://gregorygundersen.com/blog/2019/02/01/clt/
DNN을 학습시키려면 데이터셋이 필요합니다. 허나 디노이징을 위한 데이터셋을 만드는건 굉장히 어려운 일이었습니다. 디노이징을 위한 데이터셋은 [노이즈가 낀 이미지 n장 - 노이즈 없는 이미지 한장] 조합으로 구성되었는데요, 이 때 노이즈가 낀 이미지들에 포함되어있는 노이즈들은 서로 independent해야됩니다. 특히 조금씩 움직이는 객체들을 가지고 노이즈 없는 이미지를 생성하는건 더더욱 힘든 일이죠.
그런데 이렇게 노이즈 없는 이미지, 다시 말해 Ground Truth을 만들어도 여전히 남는 문제가 있습니다. 바로 노이즈가 하나도 없는 이미지를 만들 수 없다는 겁니다. mild한 노이즈들이 여전히 끼어있다는 것이죠. 그러면 DNN은 노이즈가 덜 낀 이미지를 생성하는걸 학습할 것입니다.
논문에서는 이러한 Ground Truth를 두고 'imperfect ground truth data'라고 말했습니다.
비지도 학습을 사용
앞서 말씀드렸듯 [노이즈 낀 이미지 - 노이즈가 '덜 낀' 이미지] 데이터셋으로 학습을 시키면 우리가 원하는 디노이징 네트워크를 만들 수 없습니다. 따라야할 교본이 노이즈가 '덜 낀' 이미지니까요.
그래서 노이즈가 낀 이미지를 이용한 비지도 학습(unsupervised training)으로 DNN을 학습시키고자 하였습니다. 네트워크의 출력값과 노이즈가 낀 이미지 사이의 MSE(Mean Square Error)를 줄이는 방향으로 네트워크를 학습시키는 DIP(Deep image prior)가 나왔고 이후 이미지별로 두가지 노이즈를 적용해 만든 두가지 이미지(두 노이즈는 서로 독립적이여야 합니다)를 가지고 비지도 학습으로 image restoration을 학습시키는 Noise2Noise가 나왔죠. Noise2Noise를 이용해 가우시안 노이즈를 포함한 다양한 노이즈를 제거하는 디노이징 DNN을 만들 수 있었습니다.
자기지도 학습을 사용
비지도학습에 이어 자기지도 학습으로 네트워크에게 디노이징을 학습시키려는 시도도 있었습니다. 그 중 하나가 바로 SURE(Stein’s unbiased risk estimator)입니다. SURE은 이미지마다 한가지 노이즈를 적용해 얻은 이미지를 가지고 가우시안 노이즈를 제거하는 디노이징 네트워크를 만드는 방식입니다.
SURE외에도 Noise2Void, Noise2Self 등이 나왔으나 다음과 같이 아쉬운 점들이 하나씩 있었습니다.
- Noise2Void : low noise level에서 BM3D와 같은 기존의 학습방식보다 안좋은 성능의 네트워크로 학습시킴
- Noise2Self : CellNet 데이터셋으로 학습시킬 때 좋은 성능의 네트워크를 학습시키지 못했음
그리고 Noise2Boosting이라고 Noise2Void를 개선한 방식이 있는데요, Noise2Boosting를 이용해 학습시킨 네트워크는 Super Resolution, MRI 성능 향상 등 더욱 general하게 사용될 수 있다고 합니다.
지금까지 비지도 학습, 자기지도 학습으로 디노이징 네트워크를 학습시키는 방식에 대해 간단히 알아봤습니다. 앞서 알아본 것들 중 중요한 것은 SURE와 Noise2Noise입니다. 그래서 제가 볼드체를 적용하기도 했죠.
이 둘을 기반으로 만든 학습방식은 임의로 생성한(Synthetic) 가우시안 노이즈에서 BM3D같은 기존의 디노이징 방식보다 더 뛰어난 성능을 보여줬습니다. 허나 이들을 사용하는데 있어 단점이 하나씩 있었습니다. 하나씩 알아보겠습니다.
Noise2Noise
Noise2Noise는 다양한 종류의 이미지를 디노이징 하는데 정말 좋은 성능을 보여줬습니다. 허나 앞서 말씀드렸듯 Noise2Noise를 사용하려면 이미지마다 2가지 노이즈를 적용한 두개의 이미지가 필요한데 이 때 적용한 두개의 노이즈는 서로 독립적이여야 합니다.
그러면, 두 가지 노이즈가 서로 독립적이라는걸 어떻게 증명하죠? 이론적으로 증명할 수 있는 방식이 있나요?
두 가지 노이즈가 서로 독립이라는걸 증명할 수 있는 이론적 설명은 없습니다. 그렇기에 Noise2Noise를 '노이즈가 한가지만 있는 경우' 혹은 '노이즈가 조금 낀 imperfect ground truth data가 있는 경우'에 Noise2Noise로 학습시킬 수 있는지 명확하지 않다고 말하고 있습니다.
그리고 Noise2Noise는 느리게 움직이는 객체나 광원이 있을 때 'low noise in ground truth'와 'identical underlying true image over multiple realizations' 사이에 Trade-off가 존재한다고 합니다.
저는 아래 SURE를 설명하는 부분을 통해 다음과 같이 이해했습니다.
"noise가 약해지면 true image가 약해진다는 것이니 Blur가 강해진다는(흐려진다는) 뜻이고 noise가 강해지면 true image가 강해지니 Blur가 약해진다(선명해진다)."
SURE
SURE 기반의 학습법은 가우시안 노이즈만 디노이징하는 네트워크만 학습시킬 수 있다는 한게가 있으나 mixed Poisson-Gaussian Noise, Exponential Family Noise 등 다양한 종류의 노이즈도 지울 수 있는 모델을 학습시킬 수 있는 잠재력을 가지고 있습니다. 그리고 Noise2Noise보다 느리게 움직이는 객체나 광원이 있을 때 Noise와 Blur 사이의 trade-off도 약하죠. 왜냐하면 SURE은 이미지마다 한가지 노이즈를 사용하기 때문이라고 합니다.
그러나, SURE를 기반으로 하는 학습방식은 이미지마다 한가지 노이즈만 사용할 수 있기 때문에 여러가지 노이즈를 학습에 사용할 수 없다는 단점이 있습니다. 다양한 노이즈를 제거하는걸 배울 수 있는 기회를 놓친다는 것이니 좋은게 아니죠.
SURE을 확장시켜보자
지금까지 Noise2Noise와 SURE를 조금 자세히 알아봤습니다. 저자는 Noise2Noise와 SURE을 보며 다음과 같이 두가지 질문을 던졌습니다.
- 서로 연관성이 있는 두가지 노이즈와 imperfect ground truth가 있을 때 Noise2Noise로 네트워크를 학습시키는 방식이 있지 않을까?
- SURE을 이용할 때 두가지 노이즈를 사용할 수 있는 방법은 없는걸까?
그리고 마지막으로 세번째 질문을 던졌죠.
- extended SURE는 '서로 연관된 노이즈'와 'well utilize imperfect ground truth'를 이용할 수 있지 않을까?
세번째 질문이 중요한 질문입니다. 논문의 저자가 스스로에게 던진 질문이 아닐까 싶습니다.
저자는 세번째 질문을 스스로에게 던졌고 이 논문을 통해 답을 내렸죠. 가능하다고.
저자는 SURE을 확장시킨 eSURE을 제안했고 eSURE 기반의 학습법으로 여러 종류의 노이즈가 적용된 이미지로 가우시안 노이즈를 제거하는 네트워크를 학습, SURE 기반의 학습법으로 만든 네트워크보다 좋고 Noise2Noise로 학습시킨 네트워크와 비슷한 성능을 기록했습니다.
그리고 여기에서 멈추지 않고 imperfect ground truth에 synthetic noise를 더한 이미지를 학습에 사용하는 방식도 연구했으며 이 방식으로 만든 이미지를 eSURE 기반 학습법에 사용했을 때도 SURE 기반의 학습법으로 만든 네트워크보다 좋고 Noise2Noise로 학습시킨 네트워크와 비슷한 성능을 기록했습니다.
그리고 Noise2Noise가 eSURE의 special case라는 것도 보여줄 것이라고 말하였습니다.
저자는 Noise2Noise는 서로 독립적인 가우시안 노이즈만 사용할 수 있는 eSURE라고 주장했으며 제약조건이 더 붙음에도 불구하고 eSURE과 Noise2Noise의 성능이 비슷하다고 말하였습니다.
저는 이를 "general한 데이터로 학습시킬 수 있는 eSURE가 더 좋다"는 말로 이해했습니다.
2. Background
Related Work에 해당하는 부분입니다. 원래 리뷰할 때 넘어갔는데 eSURE와 같이 자기지도 학습에 사용하는 식? 방식에 해당하는 것은 제가 잘 모르기 때문에 따로 짚고 넘어가도록 하겠습니다.
식을 정의하기 전에 몇가지 parameter들을 정의해보겠습니다. 다음과 같습니다.
- x : unknown signal
- n : 평균이 0이고 분산이 σ^2*I인 가우시안 노이즈. 여기서 I = identity matrix
- y = x + n : 가우시안 노이즈가 적용된 이미지
- h(y) : 네트워크의 출력값입니다. 즉, 네트워크가 측정한 노이즈입니다.
그리고 논문에서는 n을
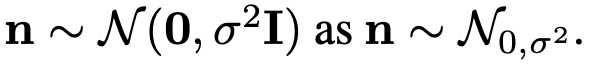
이렇게 표시하기로 했습니다.
그러면 지금부터 설명을 시작해보겠습니다.
2.1 Stein’s unbiased risk estimator (SURE)
먼저 SURE입니다. Deterministic한 신호(이미지) x를 이용해 얻은 h(y)가 있을 때, SURE는 다음과 같습니다.
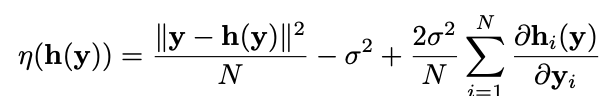
그리고 SURE는 다음의 정리를 따릅니다.
정리 1 : 확률변수 ŋ(h(y))는 다음 값의 unbiased estimator다.
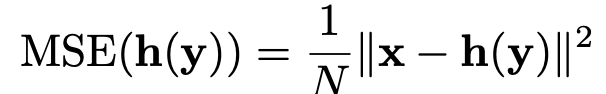
여기서 unbiased estimator는 추정값(estimator가 출력하는 값)의 기대값이 실제 값인 estimator를 말합니다.
즉, SURE로 얻은 값들의 평균은 h(y)의 MSE(Mean Squared Error, 평균 제곱 오차) 라는 말이며 이를 식으로 표현하면
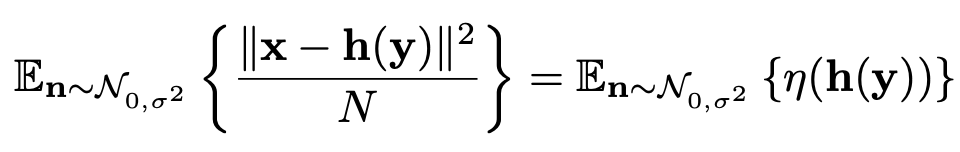
위와 같이 됩니다. 확률변수 n에 대한 MSE(h(y))와 SURE의 출력값의 기대값이 같다는 것이죠.
우리는 SURE를 이용해 estimator h(y)의 parameter들을 학습시킬 수 있긴 합니다. 허나 SURE의 마지막 항(미분이 들어간 항)이 h(y)가 linear filters 혹은 non-local mean인 경우에만 유효한 항입니다. 그렇기 때문에 우리는 SURE을 좀 더 일반적인 경우에도 사용할 수 있게 마지막 미분 항을 다른 항으로 근사시켜야 할 필요가 있습니다.
2.2 Monte-Carlo SURE (MC-SURE)
그래서 근사항이 들어간 SURE가 등장했습니다. MC-SURE은 h(y)에 대한 MSE의 unbiased한 값을 출력하며 이는 정확한 값입니다. MC-SURE은 다음의 정리를 따릅니다.
정리 2 : n이나 y에 독립적인 n ̃ = 평균이 0, 분산이 1인 가우시안 노이즈가 있을 때 다음의 식
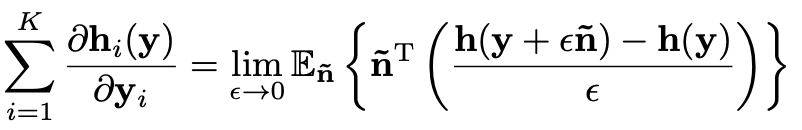
은 h(y)가 '잘 정의된' 2차 테일러 급수로 근사될 수 있음을 보여준다. 만약 위 식이 성립하지 않아도 'in weak sense'에서 h(y)를 근사시킬 수 있다는 것이 여전히 유효하다.
저는 여기서 "만약 위 식이 성립하지 않아도 'in weak sense'에서 h(y)를 근사시킬 수 있다는 것이 여전히 유효하다." 부분이 이해가 잘 안되었습니다.
원문으로는 "If not, this is still valid in the weak sense provided that h(y) is tempered"라고 쓰인 부분입니다.
아무튼, '정리 2'를 SURE의 마지막 미분항에 적용할 경우 미분항을 다음과 같이 근사할 수 있을겁니다.
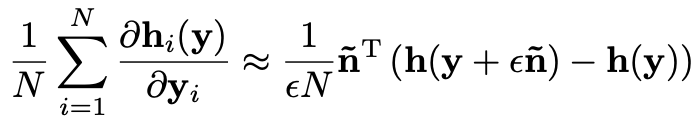
(여기서 n ̃ 은 평균이 0, 분산이 1인 가우시안 노이즈, ε는 작은 값을 가진 상수입니다.)
2.3 SURE based deep denoiser training
SURE은 네트워크의 출력값과 Ground Truth(네트워크로 만들어진 Gauissian 디노이저를 비지도 학습시킬 때) 사이의 MSE를 최소화 하는데 쓰이는 수치로 사용되고 있습니다.
특히 MC-SURE은 규모가 큰 네트워크에게 가우시안 노이즈 제거를 학습시킬 수 있게 해줍니다. 노이즈가 있는 ground truth image와 네트워크 사이의 MSE를 줄이는 방식으로 학습시키는 것이죠.
네트워크를 위한 SURE은 앞서 확인한 테일러 급수를 이용한 미분항 근사가 반영된 SURE를 조금 수정하면 만들 수 있습니다.
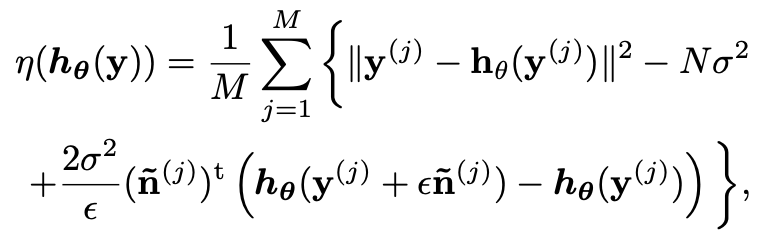
이와 같이 말이죠. h(y)를 hθ(y)로, 우항의 y와 n ̃을 y(j), n ̃(j)로 변경했습니다. 식에 나오는 일부 값들을 설명하면 다음과 같습니다.
- M : 미니배치의 크기
- ε : 작은 값을 가진 상수
- n ̃(j) : j번 째 학습용 데이터를 위한 단일 노이즈. 노이즈의 확률분포는 가우시안 분포를 따릅니다.)
위와 같이 SURE를 기반으로 만든 학습법은 가우시안 노이즈의 디노이징에서 state-of-the-art를 달성하고 MSE-trained 네트워크와 비슷하거나 조금 부족한 질적,양적 결과를 내는 네트워크를 만들었다고 합니다.
여기서 MSE-trained 네트워크는 노이즈가 없는 ground truth data로 지도학습을 했을 때 만들어진 네트워크를 말합니다. 노이즈가 하나도 없는 이미지는 비현실적인 경우이니 SURE기반 학습법이 사실상 제일 성능이 좋은 네트워크를 학습시키는 방식이라고 볼 수 있습니다.
3. Methods
Methods에서는 Noise2Noise를 재해석하고 SURE와 MC-SURE를 서로 연관있는 노이즈가 적용된 2장의 이미지로 학습시킬 수 있게 확징시킨 식을 보여주고 이를 네트워크 학습에 사용하는 방법을 보여줍니다. 하나씩 확인해봅시다.
3.1 Revisiting Noise2Noise
Noise2Noise는 서로 독립적인 노이즈가 적용된 2장의 이미지를 사용하며 이 때 사용되는 노이즈로 zero-mean noise를 요구합니다. 즉, Correlation이 하나도 없는 White Ganssian Noise를 요구하는 것이죠. 출처 그러나 두 노이즈가 서로 독립적이라는 것을 보여줄 명확한 전제가 없습니다.
그런데, '경험적으로' 서로 독립된 노이즈가 적용된 두 이미지를 사용할 수 있다고 합니다. 지금부터 알아보겠습니다.
joint distribution을 가진 확률변수 x, y, z가 있고 두개의 노이즈 벡터 y-x, z-x이 각각 가지는 기대값이 크기가 0인 벡터라고 가정해봅시다. 그러면 이들을 가지고 구한 MSE for infinite data는
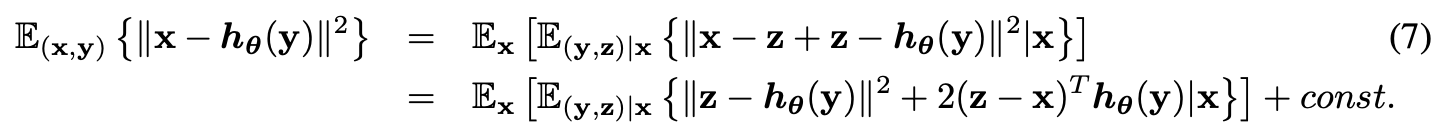
위와 같습니다. (모든 데이터를 사용한다는 의미로 j를 표시하지 않고 for infinites data라고 나타낸듯 합니다)
여기서 만약에, x가 고정된 값일 때 y와 (z-x)가 uncorrelated 하거나 서로 독립적이면 위 식은 Noise2Noise loss function이랑 같은 값이 됩니다.
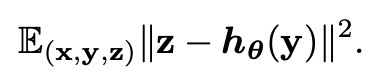
그러므로 이 식을 이용해 얻은 네트워크 hθ(y)는 clean ground truth를 가지고 MSE로 학습시킨 네트워크와 같은 parameter θ를 가지게 되며 이러한 조건에서 Noise2Noise로 학습시킨 네트워크는 뛰어난 성능을 보여줬습니다.
우리가 알 수 있는 것
우리는 앞서 수행한 분석을 통해 알아낸 사실이 무엇일까요? 바로 Nois2Noise를 이용해 네트워크를 학습시킬 때 사용하는 두 이미지에 적용된 노이즈가 uncorrelated 하거나 독립적이여야 좋은 성능을 가진 네트워크로 학습시킬 수 있다는 겁니다. 굉장히 제약이 크죠.
그렇기에 대부분의 경우, 그러니까 데이터가 imperfect ground truth images x ̃ 와 약한 노이즈인 경우에는 두 종류의 데이터가 서로 uncorrelated 하거나 독립적이지 않기 때문에 Noise2Noise로 학습시켜도 좋은 성능의 네트워크를 만들 수 없습니다.
3.2 Extended SURE and MC-SURE
우리는 3.1에서 SURE가 Noise2Noise와는 달리 여러 종류의 노이즈가 적용된 이미지를 사용할 수 없다는 단점이 있음을 알아냈습니다. 이번 섹션에서는 앞서 Introduction에서 말한 여러 종류의 노이즈를 사용할 수 있는 '확장된' SURE가 등장합니다. ground truth image마다 여러 종류의 노이즈를 적용한 이미지들로 네트워크를 학습시킬 수 있는 extended SURE(eSURE)가 등장하는 것이죠.
eSURE에 대한 정리는 다음과 같습니다.
정리 3 : 다음과 같은 확률변수들이 있다고 하자.
y1 : 평균이 x, 분산이 (σ_y1)^2*I인 가우시안 분포를 따르는 imperfect ground-truth image
z : 평균이 0, 분산이 (σ_z)^2인 AWGN(Additive White Gaussian Noise)
y2 = y1 + z : 평균이 x고 분산이 ((σ_y1)^2 + (σ_z)^2)*I인 가우시안 분포를 따르는 noisy image
위 변수들이 존재할 때, 확률변수 γ(hθ(y2),y1)는 다음 MSE의 unbiased estimator다.
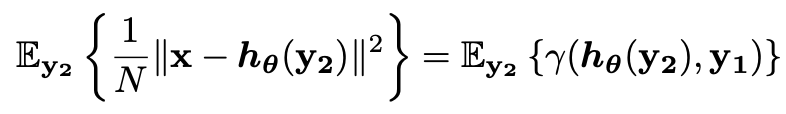
이 때 y1과 z는 서로 독립적이거나 uncorrelated하며 γ(hθ(y2),y1)는 다음과 같이 정의할 수 있다.
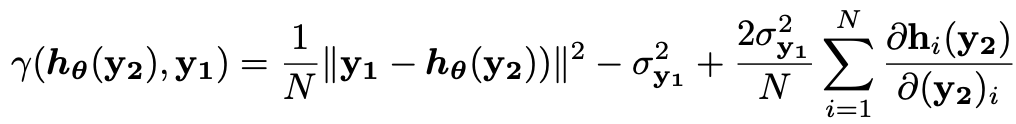
정리 3은 노이즈가 많은 이미지를 디노이징하는 네트워크를 학습시킬 때 약한 노이즈가 있는 imperfect ground truth images를 이용할 수 있을 경우에 사용하라고 만든 식입니다.
그리고 정리 3을 이용해 또다른 정리(Corollary)도 만들 수 있습니다. 다음과 같습니다.
Corollary : 다음과 같은 확률변수들이 있다고 하자.
y3, y4 : 깨끗한 이미지에 노이즈를 적용한 것들(a noisy realization pairs), 평균 x, 분산 (σ_y)^2*I인 가우시안 분포를 따른다.
w = 0.5 (y3 + y4) : 노이즈가 약해진 이미지. x, 분산 0.5(σ_y)^2*I인 가우시안 분포를 따른다
z : 평균 0, 분산 0.5(σ_y)^2I인 가우시안 노이즈
v = (w + z) : w에 z가 적용된 노이즈 낀 이미지. 평균 x, 분산 (σ_y)^2*I인 가우시안 분포를 따른다
위 변수들이 있는 상황에서 정리 3의 식을 적용하고 마지막 미분항에 Monte-Carlo 근사를 적용해 값을 바꾼다면
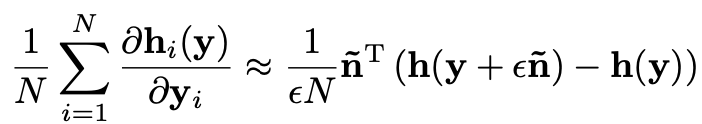
우리는 다음과 같이 θ에 대한 최소값을 만들 수 있는 extended MC-SURE을 만들 수 있다.
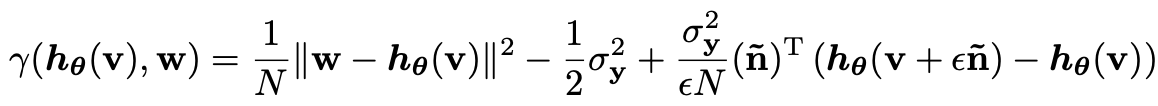
위 식을 이용해 우리는 M개의 노이즈 이미지 {(y3(1), y4(1)), · · · , (y3(M), y4(M))}로 M개의 {(w(j), v(j))}(1<=j<=M)을 만들어 네트워크에게 디노이징을 학습시킬 수 있으며 시뮬레이션 결과, eSURE 기반의 학습법으로 만든 네트워크는 MC-SURE 기반의 학습법으로 만든 네트워크보다 흑백, 컬러 이미지 디노이징에서 더 좋은 성능을 보여줄 것이라는 결론이 나왔습니다.
실제 성능 비교는 Experiment에서 확인하실 수 있습니다.
3.3 Link between eSURE and Noise2Noise
eSURE는 다음과 같이 서로 uncorrelated한 이미지들도 받을 수 있습니다.
- y : 평균 x, 분산 (σ_y)^2*I인 가우시안 분포를 따르는 Gaussian noisy image
- z : 평균 x, 분산 (σ_z)^2*I인 가우시안 분포를 따르는 Gaussian noisy image
만약 y, z로 eSURE의 값을 구하게 된다면 그 기대값은 다음과 같이 마지막 미분항이 사라진 값이 됩니다.
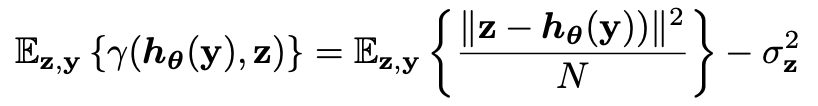
증명은 다음과 같습니다.
여기서 첫 번째 항은 가우시안 노이즈를 디노이징하는 네트워크를 만들 때 Noise2Noise의 cost function과 상응한다고 합니다.
그러므로 위 식으로 얻은 값을 최소화하는 방향으로 네트워크를 훈련시킨 결과는 Noise2Noise를 이용한 학습법으로 만든 네트워크와 같습니다. 즉, eSURE와 Noise2Noise가 same solution을 가지고 있다는 뜻입니다.
그리고 Noise2Noise는 두 종류의 노이즈가 서로 독립적이여야 된다는 매우 특별한 조건이 요구되는데 eSURE은 독립 여부에 상관없이 두 종류의 노이즈가 있으면 되므로 Noise2Noise는 가우시안 노이즈를 디노이징할 때 사용하는 eSURE, 특히 extended MC-SURE기반의 학습법의 special case라고 볼 수 있습니다.
4. Results
성능 확인을 하는 단계입니다. 실험 과정과 결과를 정리해놓은 부분이죠.
4.1 Experimental setup
수행한 실험에 대해 소개하고 있습니다. 총 2개의 실험을 수행했는데요, 각 실험의 목적은 다음과 같습니다.
- 첫 번째 실험 : eSURE가 효율적으로 이미지당 적용된 두 종류의 uncorrelated한 노이즈를 사용할 수 있으며 그 성능이 SURE을 능가함을 보여주고 eSURE가 Noise2Noise를 보다 general하게 사용할 수 있는 버전이라는 것도 보여주고자 함.
- 두 번째 실험 : imperfect ground truth가 있을 때 적용할 노이즈들이 서로 correlation을 가지는 정도에 따른 Noise2Noise와 eSURE의 성능 비교를 하고자 함
그리고 실험에서 비교를 위한 네트워크로 BM3D, DnCNN을 선택했는데요, 다음과 같이 준비했습니다.
- MC-SURE기반 학습법으로 만든 BM3D, DnCNN(자기지도 학습)
- Noise2Noise기반 학습법으로 만든 BM3D, DnCNN(비지도 학습)
- noiseless ground truth data를 이용해 MSE로 학습시킨 DnCNN (지도 학습)
학습법에 따른 성능을 비교할 목적으로 네트워크를 준비한 것이죠.
마지막으로 실험에 사용한 테스트용 데이터셋은 Berkeley’s BSD-68, Set 12을 준비했습니다.
그 외 실험에 대한 설정이 있으나 생략했습니다. 자세한 실험 내용은 논문에서 확인하실 수 있습니다.
4.2 Case I: two uncorrelated noise realizations per one image
첫 번째 실험은 BSD-400에 있는 이미지를 50x50 크기의 조각(patch)으로 잘게잘게 나눠 128 x 2919개의 조각을 생성한 뒤 조각별로 서로 독립적인 두 종류의 노이즈를 적용했습니다.
그런데 MC-SURE은 한 종류의 노이즈만 사용할 수 있습니다. 그래서 생성한 두 종류의 노이즈를 서로 다른 이미지에서 나온 노이즈로 취급하는 데이터셋을 생성해 MC-SURE기반 학습법으로 DnCNN을 학습시킬 때 사용했습니다. 사용하는 데이터셋의 종류는 같은데 학습할 때 사용하는 방식을 다르게 한 것이죠. 이 방식으로 만든 네트워크는 테이블에 DnCNN-SURE*라고 표시했습니다.
학습 방법도 자세히 설명해줍니다. 이미지를 조각조각내면 에포크마다 이를 뒤섞습니다. 그러면 네트워크가 만나게 될 조각의 순서가 뒤죽박죽이 될겁니다. 학습시킬 때 셔플하는거랑 같다고 보시면 될듯 합니다. 이렇게 셔플을 학습에 적용해 σ ∈ [0 − 55] 수준의 노이즈를 디노이징하는 네트워크를 학습시켰습니다.
그 외 학습시 사용한 세팅은 다음과 같습니다.
- 옵티마이저 : Adam
- 학습률 : 1~40 에포크에서 0.001, 41~50 에포크에서 0.0001'
실험결과는 다음과 같습니다.

실험결과를 통해 eSURE로 학습시킨 네트워크가 Noise2Noise(N2N), SURE, SURE*보다 모든 부분에서 가장 좋은 성능을 보여주고 지도 학습으로 만든 네트워크보다 약간 뒤떨어지는 성능을 보여줬다는 사실을 확인할 수 있습니다. 지도 학습으로 만든 네트워크는 현실적으로 구현하기 어렵기 때문에 사실상 eSURE로 만든 네트워크가 노이즈를 제거하는데 있어 가장 좋은 성능을 보여준다는 것을 확인할 수 있습니다.
4.2 Case II: two correlated noise realizations per one image - imperfect ground truth
이번에는 imperfect ground truth와 두 종류의 correlated noise가 있는 경우입니다. 실제로 데이터를 구하는 경우에 해당된다고 볼 수 있죠. 앞서 Introduction에서 말씀드렸듯 우리가 ground truth image라고 판단한 것들도 아주 미약하게나마 노이즈가 첨가된 이미지들이라 imperfect ground truth이며 여기에 데이터셋 생성을 위해 임의로 생성한 노이즈(synthetic noise)를 추가합니다. 그런데 이 때 생성된 노이즈들은 서로 연관성이 있는 노이즈이죠.
이번 실험은 생성된 노이즈간의 연관성이 eSURE, Noise2Noise, SURE의 성능에 얼마나 영향을 미치는지 알아보는 목적으로 수행되으며 실험은 다음의 2가지 세부 실험으로 구성되어 있습니다.
- grayscale BSD-400에 고정된 값의 노이즈를 적용한 사진들을 디노이징
- color BSD-432에 blind noise (σ_noisy ∈ [σ_gt − 55])를 적용한 사진들을 디노이징(σ_gt는 임의로 만든 가우시안 노이즈의 표준편차입니다)
실험 과정은 사용하는 이미지만 제외하면 Case 1에서 수행했던 실험과 같습니다. 패치 단위로 이미지를 쪼갠 뒤 학습 시키고 성능을 확인하는 것이죠. 학습에 사용한 parameter도 Case 1과 같습니다.
실험 결과는 다음과 같습니다. 단위는 PSNR입니다.
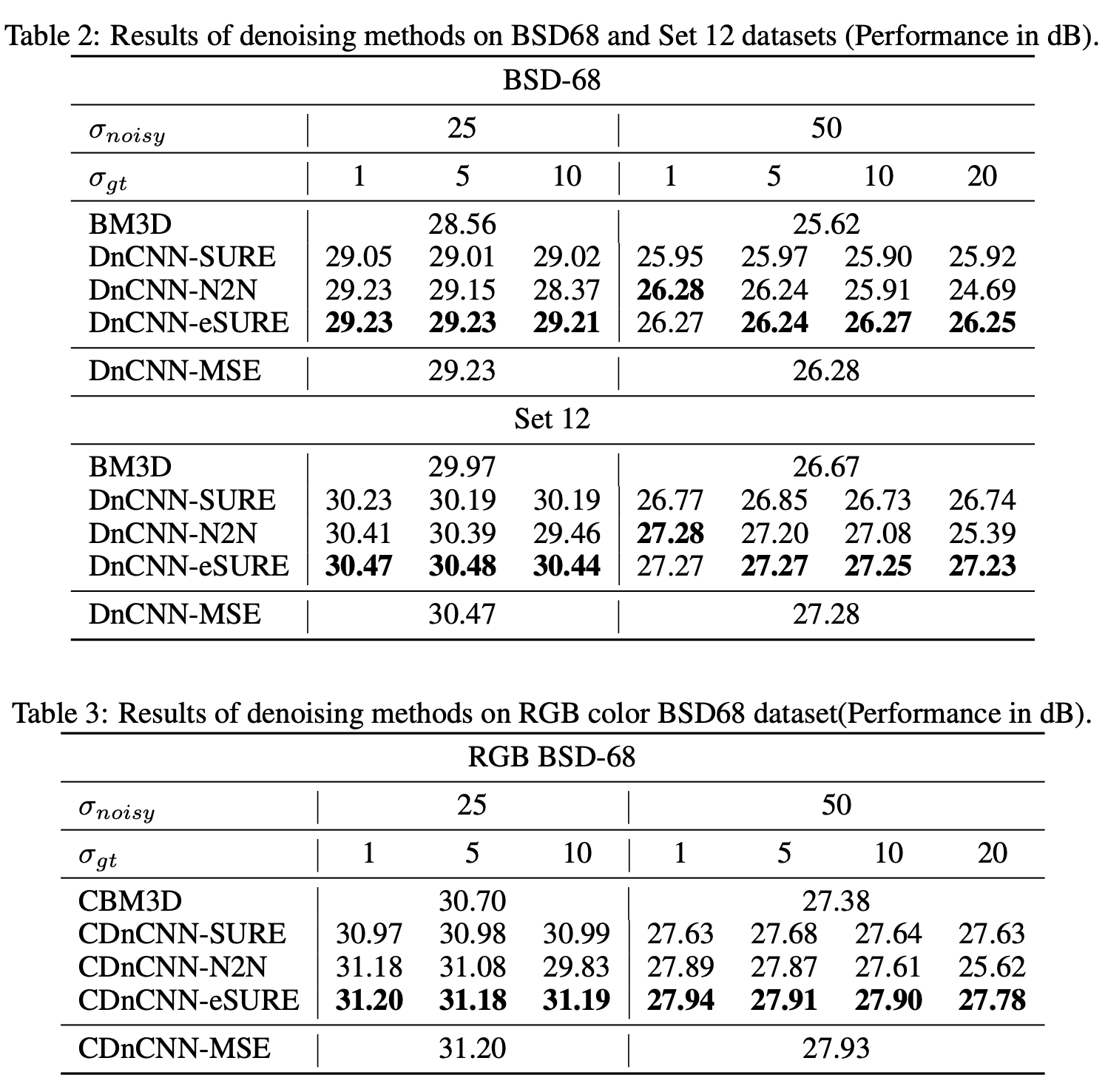

여기서는 지도학습으로 만든 네트워크를 포함해도 eSURE를 기반으로 학습시킨 네트워크가 대부분의 항목에서 가장 좋은 성능을 보여주고 있음을 확인할 수 있습니다. σ_gt가 1이고 σ_noisy가 50인 상황은 Noise2Noise 기반 학습법으로 학습시킨 DnCNN의 성능이 제일 좋네요.
그리고 마지막으로 σ_gt가 1~10인 데이터셋으로 네트워크를 학습시키고 σ_noisy가 25, 50인 경우인 이미지로 디노이징 성능을 확인하는 실험을 했습니다. 더 현실적인 경우에서 실험을 한 것입니다. 결과는 다음과 같습니다.

eSURE기반 학습법으로 학습시킨 DnCNN이 지도 학습으로 학습시킨 CDnCNN-MSE을 포함한 모든 네트워크 중 가장 좋은 성능을 보여주고 있음을 알 수 있습니다.
테이블에서 CDnCNN이라고 나타낸 이유는 사용한 데이터셋이 'RGB color dataset'여서 DnCNN 앞에 C를 붙힌게 아닌가 싶습니다.
5. Conclusion
논문의 결론 부분입니다. 논문의 내용이 잘 요약되어있습니다. 자세한 내용은 논문에서 확인하실 수 있습니다.
리뷰 후기
어우...힘들었습니다. 이러한 cost function을 리뷰하는건 처음이라 그런듯 합니다.
그래도 리뷰하니까 좋았습니다. 여태까지 시도하지 않았던 종류의 논문을 이렇게까지 자세히 읽고 리뷰한 경험이 없었기 때문에 향후 다양한 종류의 논문을 읽을 때 이번 논문 리뷰 경험이 저에게 큰 힘이 되지 않을까 싶습니다.
다음에도 기회가 된다면 이와 같이 네트워크가 아닌 다른 요소에 관한 논문을 다뤄보도록 하겠습니다.
그러면 다음 논문에서 뵙겠습니다.