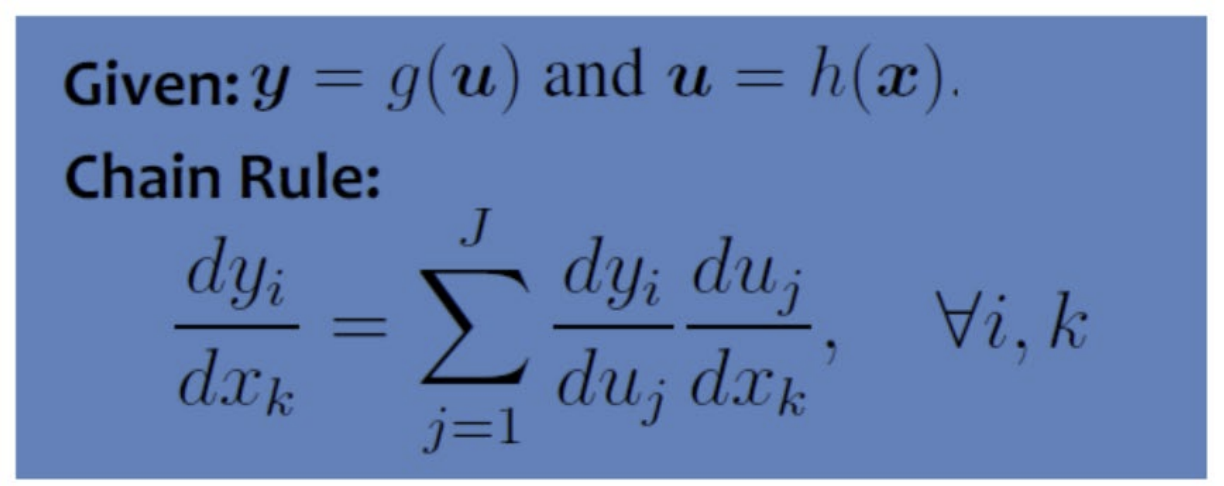Back-propagation

Background: Chain rule of calculus

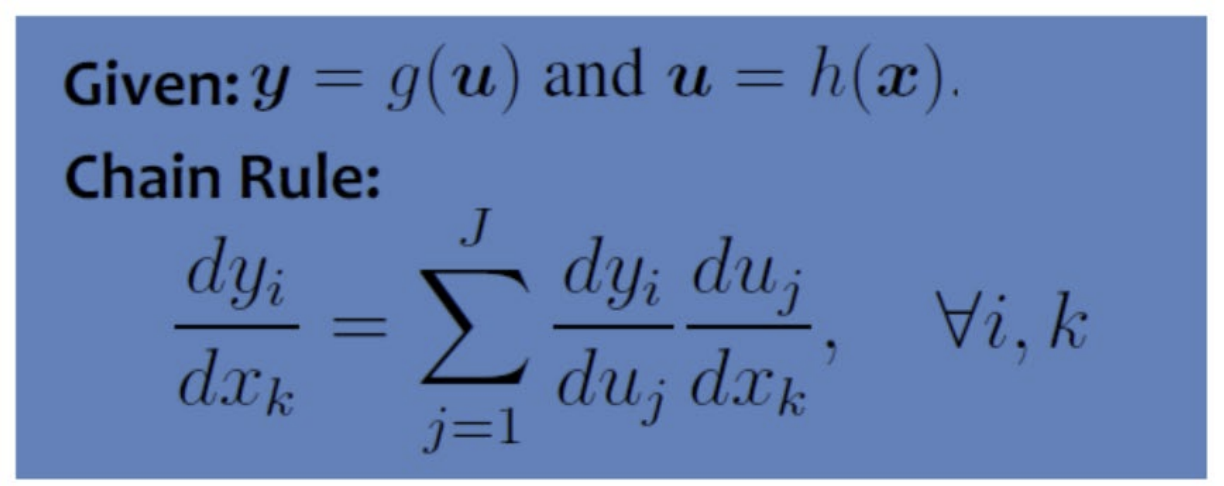
• input x는 u(h(x))와 연결, u는 g(u)와 연결, g(u)는 output y와 연결되어 있음
• Chain Rule: 합성함수의 미분 == 합성함수를 구성하는 각 함수의 미분(partial derivative==편미분)의 곱
  => Backpropagation은 chain rule을 반복하여 적용한 것!

Computational graph

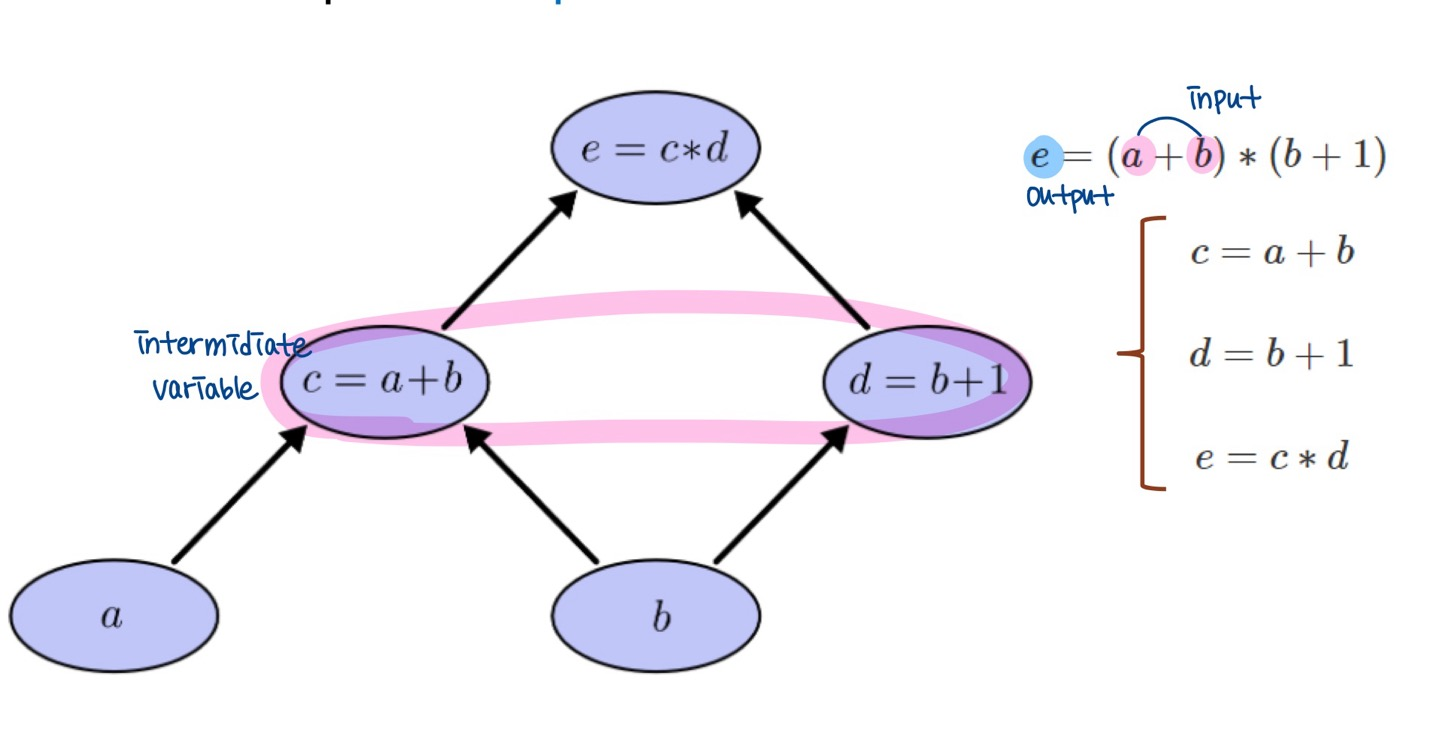
• 노드가 연산(operation)이나 변수(variable)에 해당하는 그래프
  • 변수간의 연결관계를 표현!

Derivatives on Computational Graphs

• 계산 그래프의 도함수(derivative)도 표현한다면?

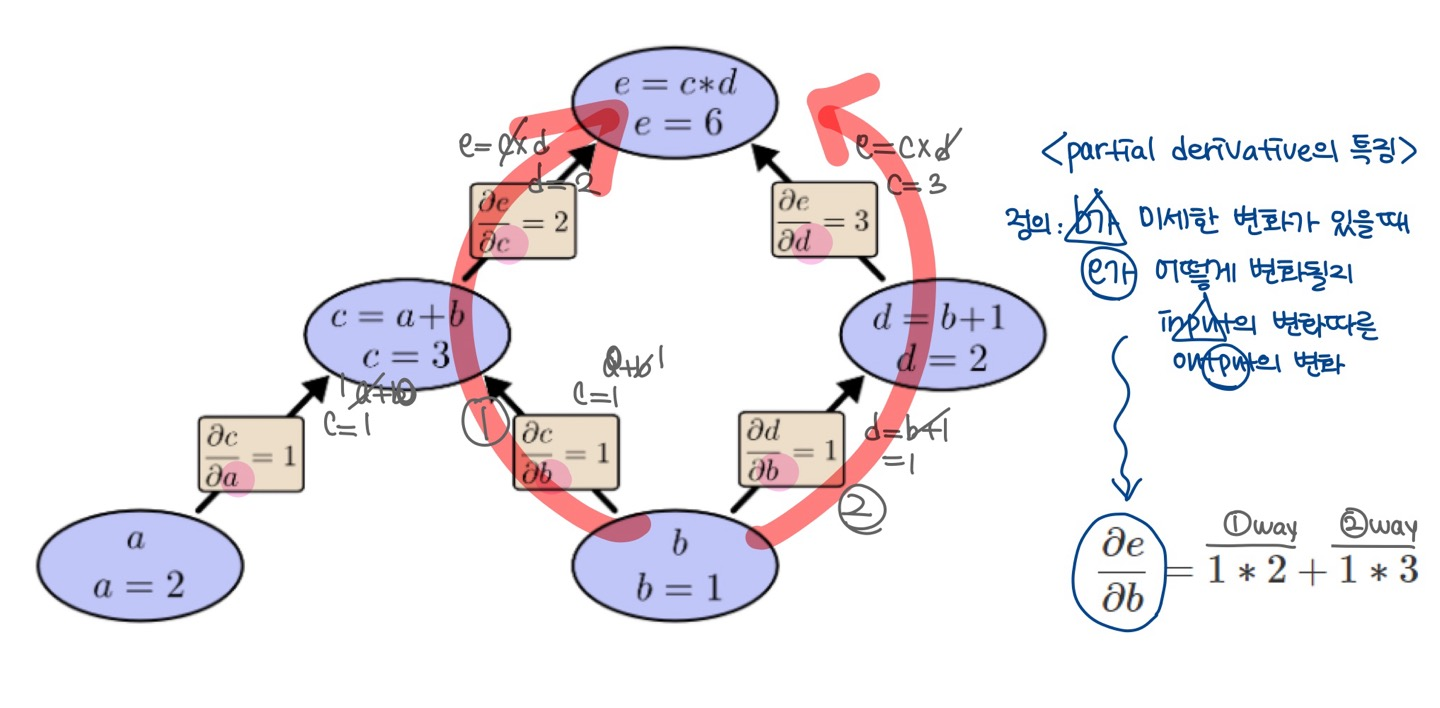
• 편미분(partial derivative)의 특징
  • 입력 변수(input)에 따른 output의 변화
    • 즉, 그림에서는 b에 미세한 변화가 있을 때 e가 어떻게 변화될지를 나타냄 (편미분에서는 다른 input인 a를 상수취급함으로 a의 변화는 고정됨)

Functions as boxes

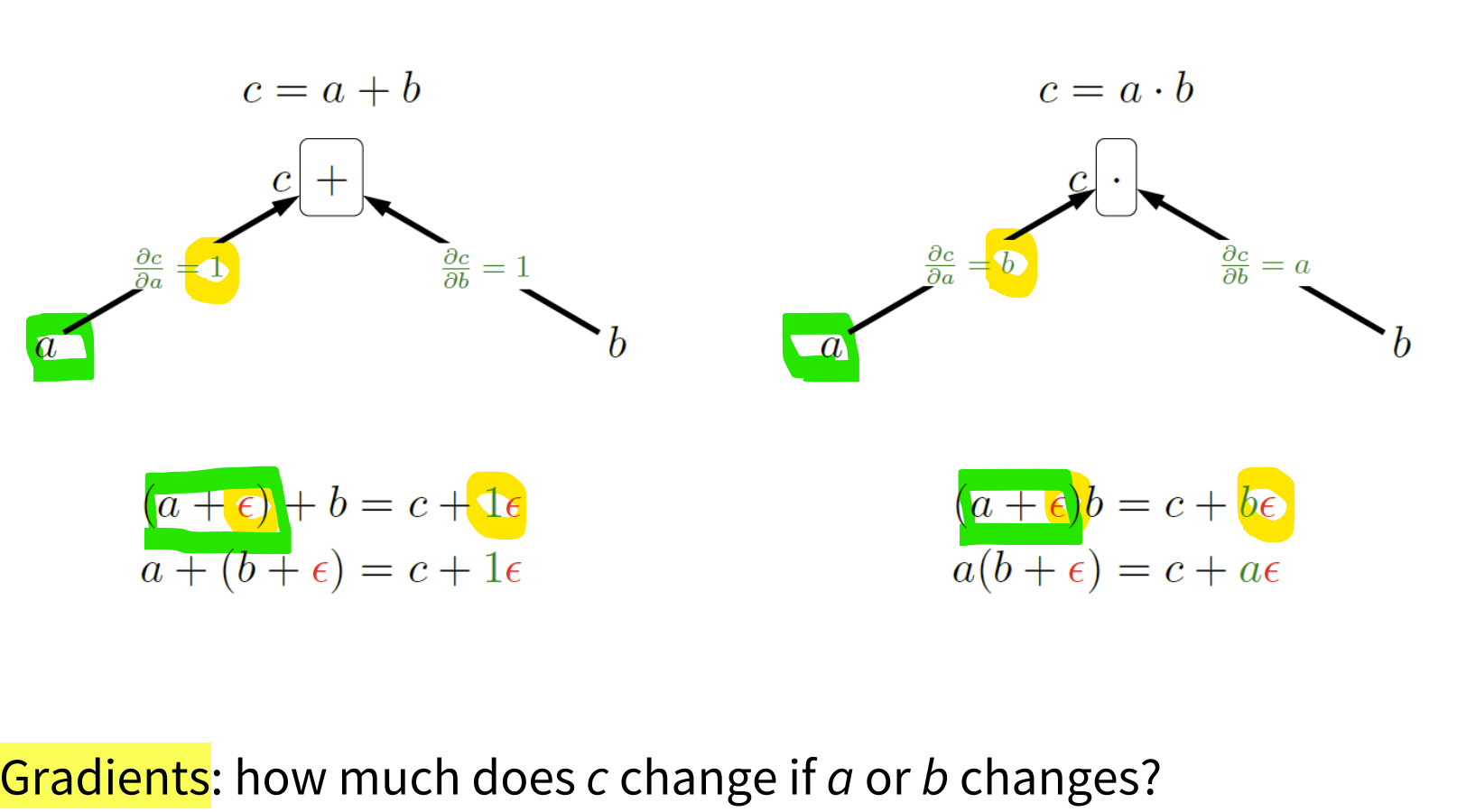
• input이 a에서 a+ε(미세한 변화)로 변했을 때 output?
  => c+1ε로 각 partial derivative(==gradient)만큼의 변화가 생김!!
• 즉, input이 변화하면 그 input의 변화의 편미분 곱만큼의 변화가 output에도 생김

• 우리 network의 최종 목표: Loss function(network의 출력 값과 label의 차이) 최적화
  - loss를 최대한 줄여야함
  • 편미분을 통해, 입력 변화에 따른 손실 함수의 변화(==입력 값 중 하나를 조금 변경했을 때 손실 함수가 얼마나 커지거나 작아지는지)를 알 수 있기 때문에 loss가 너무 클 때 어떤 input을 줄여야할지 알아내어 최적화할 수 있음!

Basic building blocks

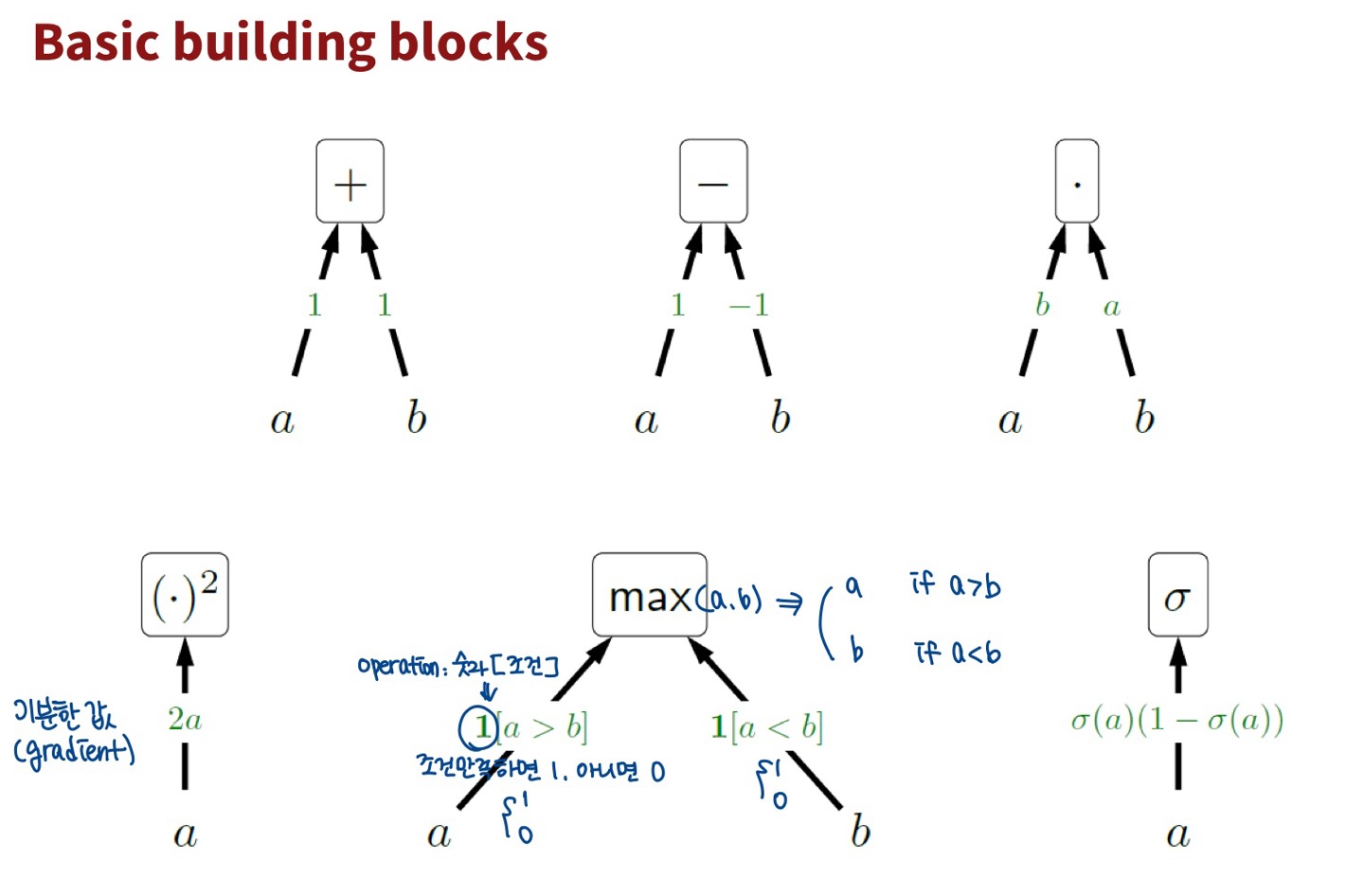
• max의 미분 => operation: 숫자[조건] (== 조건을 만족하면 숫자, 아니면 다른값)
  - 1[a>b]: a>b이면 1, 아니면 0

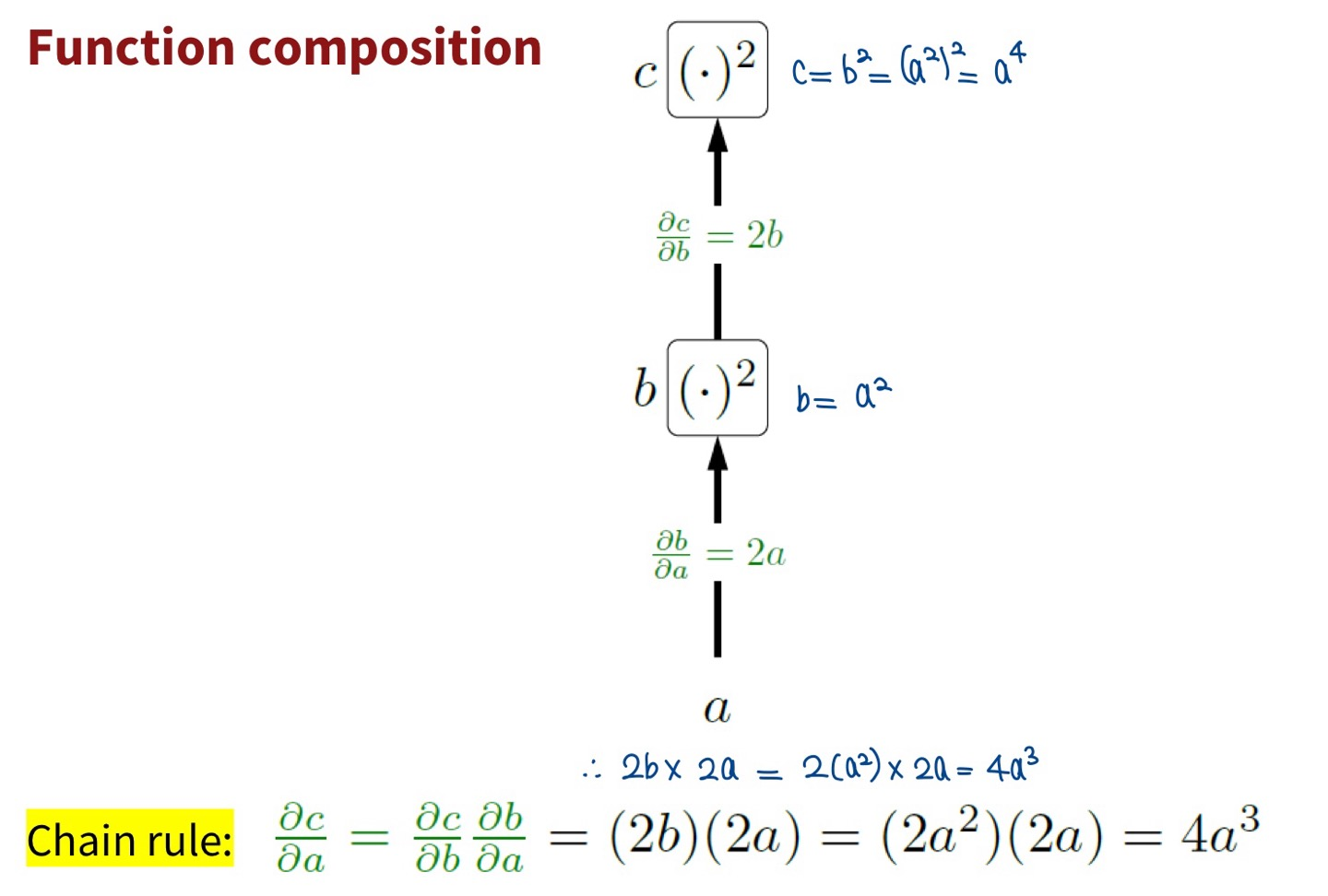
Function composition

Linear classification with hinge loss

• hinge loss

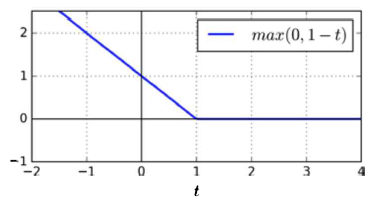
• input >1이면, loss 0
  input <1이면, loss 엄청 큼

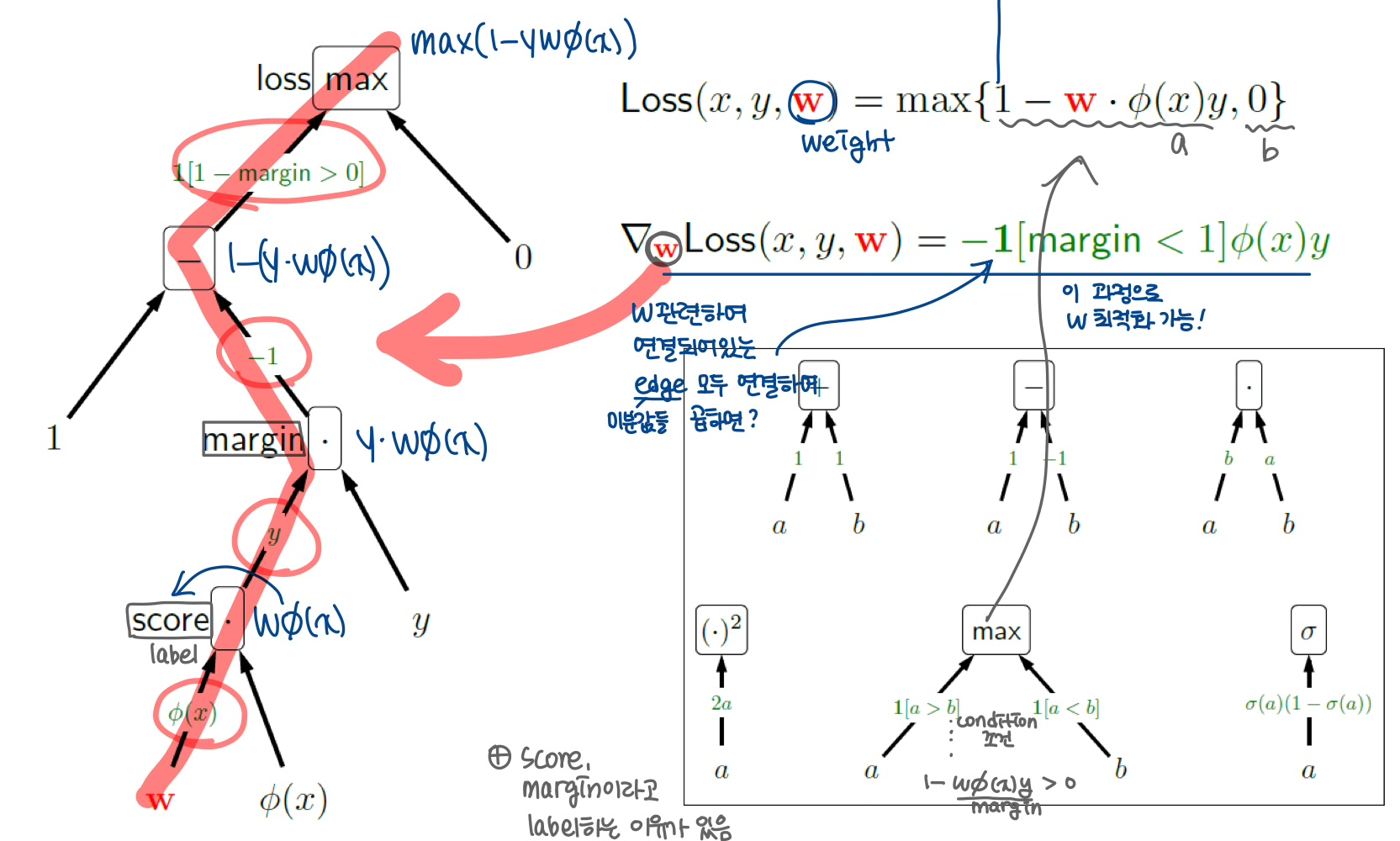
• 파라미터(w)(==input중 최적화해야하는 값)와 연관된 파라미터들의 편미분값을 모두 곱하면? -> loss를 최소화하도록 w최적화 가능!

1. score라고 부르는 이유? :
2. margin이라고 부르는 이유? :

Forward- & Back-propagation

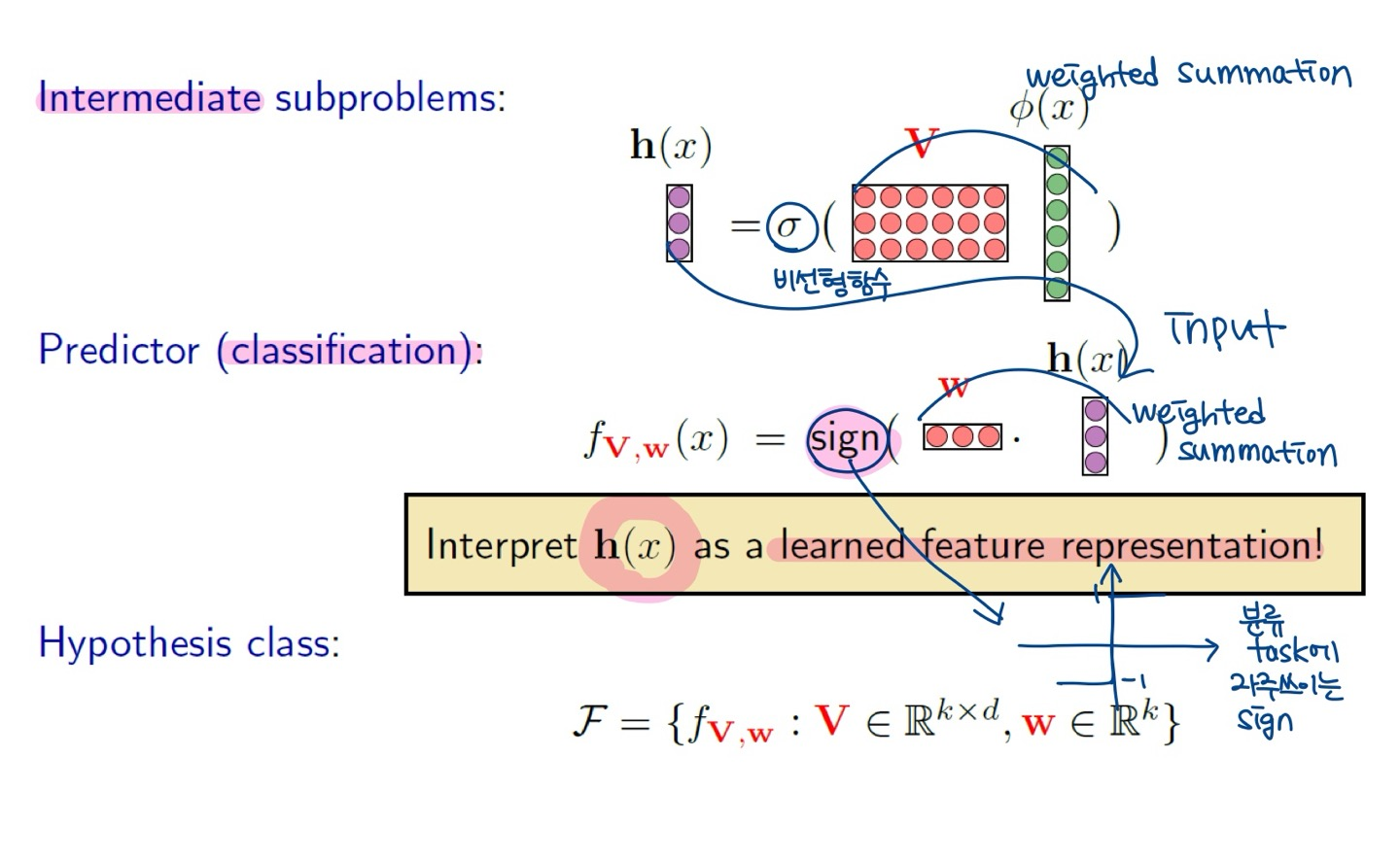
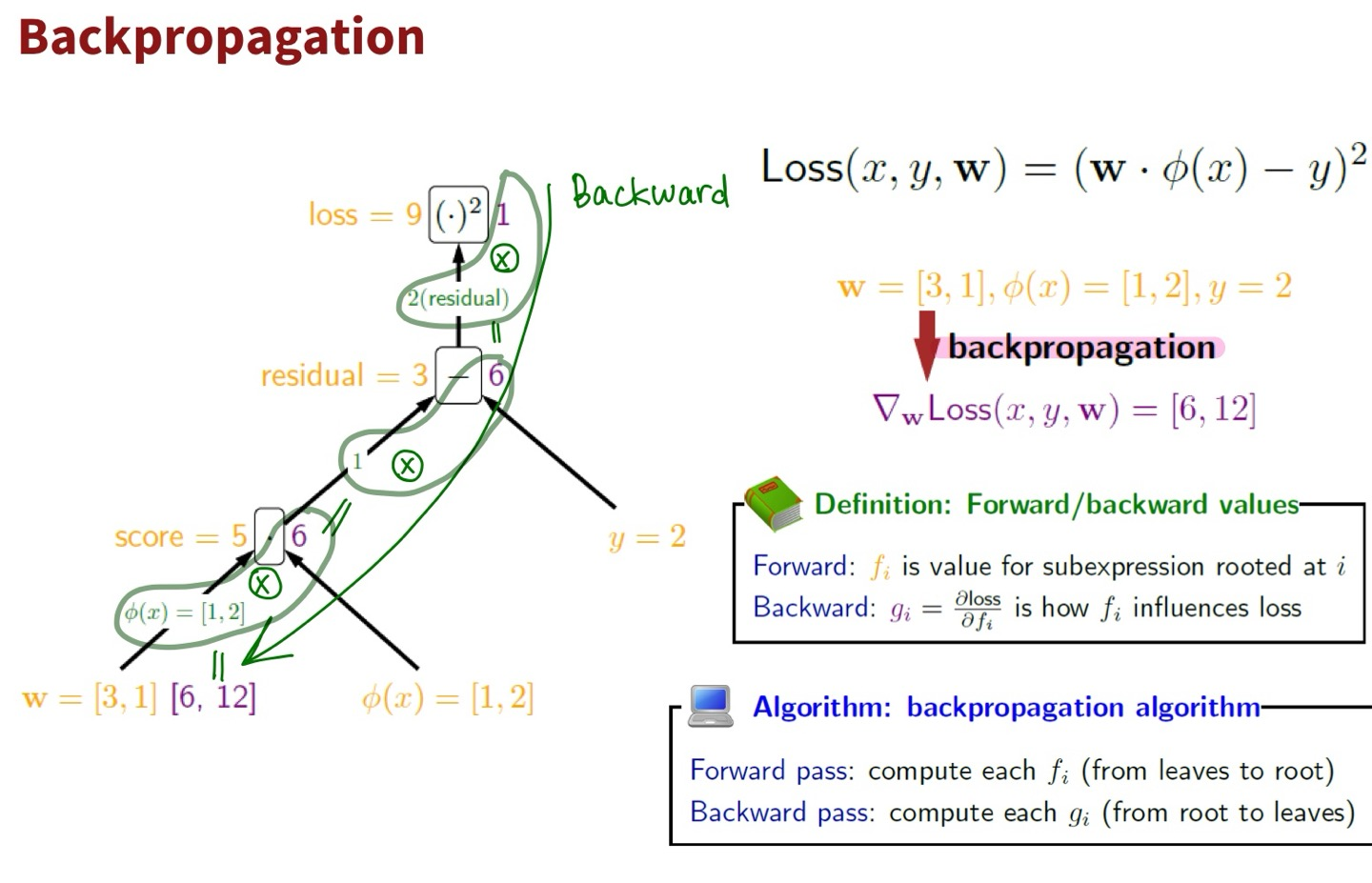
• Algorithm: backpropagation algorithm
  • Forward pass: 루트에서 시작하여 순차적으로 계산 (즉, 입력에서 시작해 모델의 출력까지 구함)
  • Backward pass: 루트에서부터 시작해 역으로 계산 (즉, 출력에서 시작해 입력 방향으로 손실 함수의 변화율을 계산)

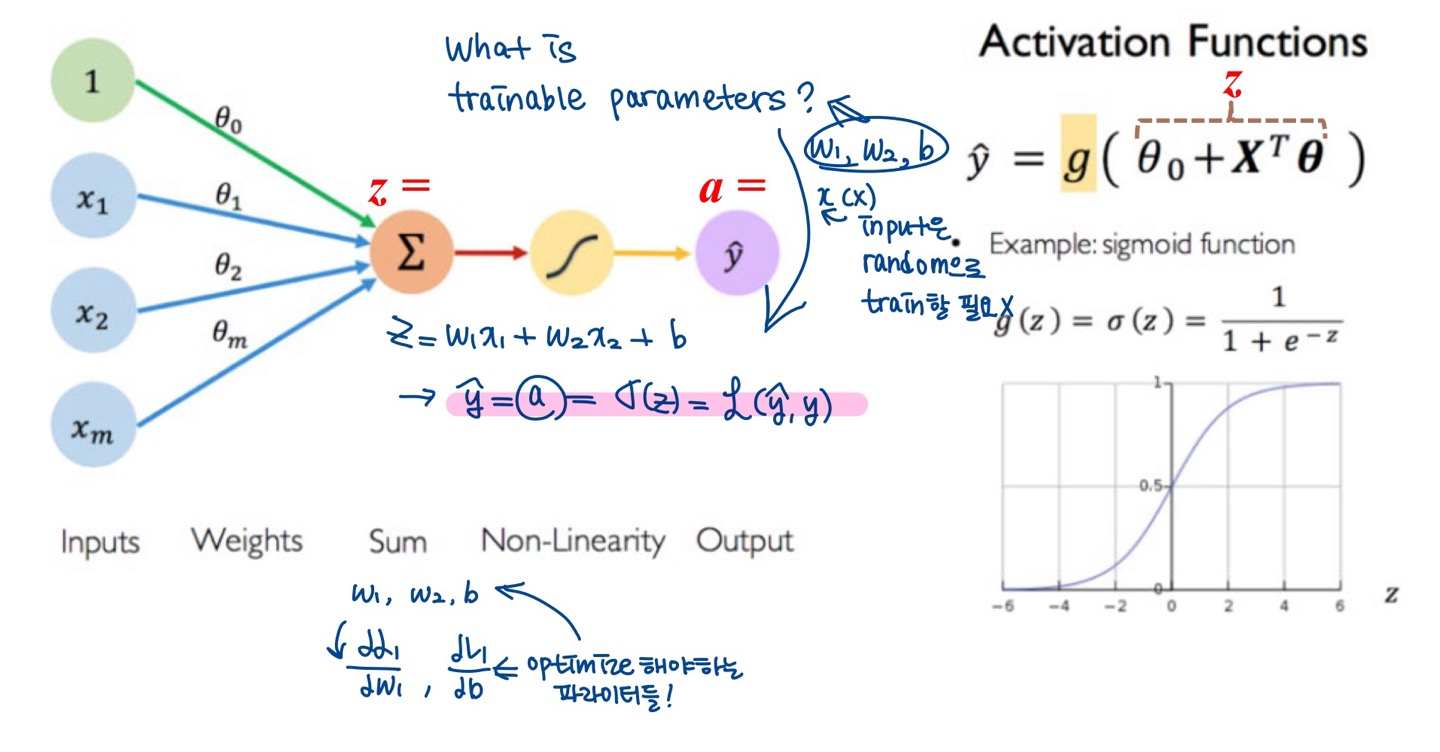
1-layered NN (== logistic regression model)의 backpropagation

Gradient Descent algorithm 공식 유도

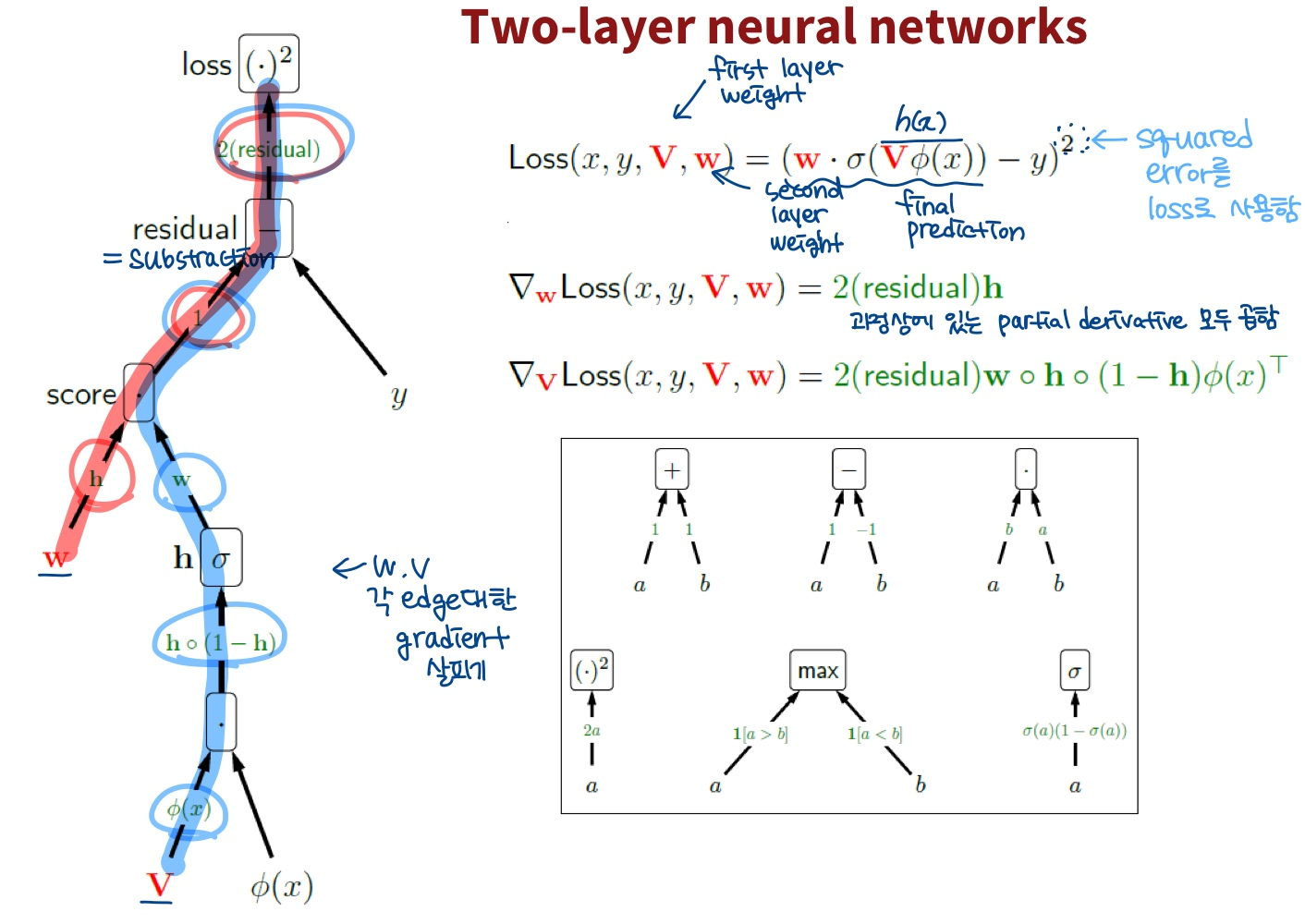
2-layered NN의 backpropagation

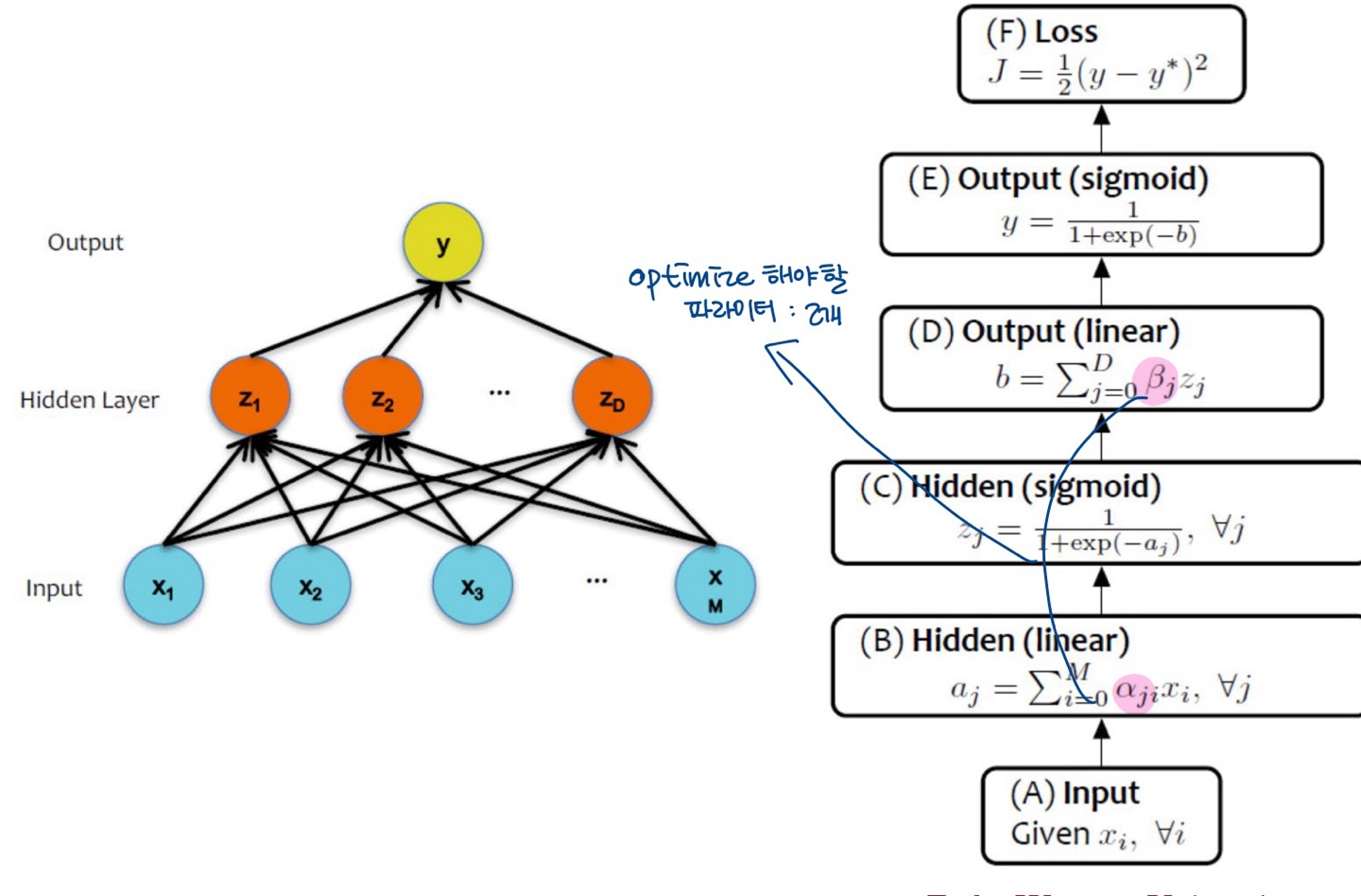
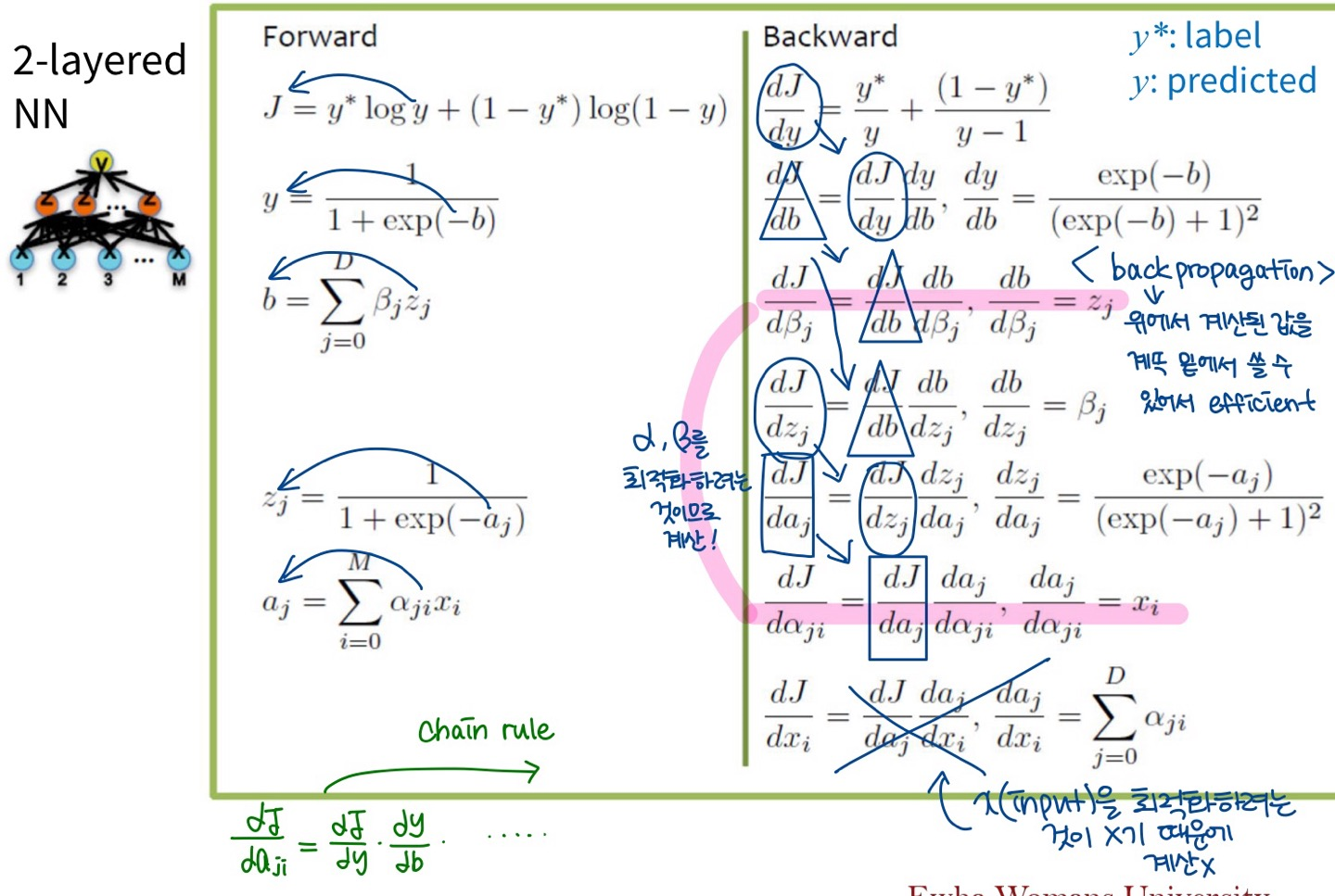
• 최적화가 필요한 파라미터만 편미분 계산하면 ok!