2. Gradient desecent variants

What is Gradient desecent algorithms?
함수의 기울기(경사)를 구하여 기울기가 낮은 쪽으로 계속 이동시켜 극값(최적값)에 이를 때까지 반복하는 것이다.
해당 함수의 최소값 위치를 찾기 위해 비용 함수(Cost Function)의 경사 반대 방향으로 정의한 Step Size를 가지고 조금씩 움직여 가면서 최적의 파라미터를 찾으려는 방법이다.
경사 하강법에서는 학습시 스텝의 크기 (step size)가 중요하다. 학습률이 너무 작을 경우 알고리즘이 수렴하기 위해 반복해야 하는 값이 많으므로 학습 시간이 오래걸린다. 그리고 지역 최소값(local minimum)에 수렴할 수 있다. 반대로 학습률이 너무 클 경우 학습 시간은 적게 걸리나, 스텝이 너무 커서 전역 최소값(global minimum)을 가로질러 반대편으로 건너뛰어 최소값에서 멀어질 수 있다.
이와 같은 문제점을 해결하기 위해 사용하는 방법으로 모멘텀이 있다. 쉽게 말해 기울기에 관성을 부과하여 작은 기울기는 쉽에 넘어갈 수 있도록 만든것이다.

Depending on the amount of data, we make a trade-off between the ccuracy of the parameter update and the time it takes to perform an update.

2.1 Batch gradient descent

As we need to calculate the gradients for the whole dataset to perform just one update, batch gradient descent can be very slow and is intractable for datasets that do not fit in memory. Batch gradient descent also does not allow us to update our model online, i.e. with new examples on-the-fly.

전체 데이터셋에 대한 cost function의 합으로 objective function J를 사용한다.
매우 느리지고 메모리에 맞지 않는 데이터는 사용할 수 없다. 또한 온라인에서는 모델을 업데이트할 수 없다는 단점이 있다.

모든 자료를 다 검토해서 내 위치의 기울기를 계산해서 갈 방향을 찾겠다.

2.2 Stochastic gradient descent

한 번 업데이트를 하기 위해 전체 데이터셋을 계산하여 학습 속도가 느린 Batch 알고리즘을 개선하기 위해 등장하였다.
BGD와이 차이점은 objective function J의 형태이다. SGD는 한 번의 업데이트를 하나의 데이터로만 이루기 때문에 빠르게 진행된다. 이로 인해 파라미터의 변화가 큰 편이며 BGD에서 자주 발생하는 local minimum에 빠지는 현상이 SGD에서는 잘 나타나지 않는다는 장점이 있다.

전부 다보는 건 너무 오래 걸리니까 조금만 보고 빨리 판단. 같은 시간에 더 많이 간다.

2.3 Mini-batch gradient descent

하지만 파라미터의 큰 변화로 global minimum을 방해하는 단점이 있기 때문에 이 둘의 중간점인 하나의 데이터가 아닌 하나의 데이터셋을 사용하는 알고리즘이 나오게 되었다.

This way, it a) reduces the variance of the parameter updates, which can lead to more stable convergence; and b) can make use of highly optimized matrix optimizations common to state-of-the-art deep learning libraries that make computing the gradient w.r.t. a mini-batch very efficient.

파라미터 업데이트의 분산을 줄여서 수렴에 좀 더 안정적이고, 최신 딥러닝 기술에 활용하기 좋다.

3. Challenges

• Choosing a proper learning rate can be difficult.
learning rate가 너무 작은 경우 수렴이 늦어지고, 너무 큰 경우 최솟값 주변에만 돌게 된다.

• Learning rate schedules [18] try to adjust the learning rate during training by e.g. annealing,
데이터 셋의 특성에 따라 조절하기가 어려워진다.

• the same learning rate applies to all parameter updates.
매 배치마다 같은 학습률을 사용하기 때문에 흔하지 않은 특성에 대해 너무 자주 업데이트가 될 수 있다.

• avoiding getting trapped in their numerous suboptimal local minima.
global minimum을 피하는 과정에서 오류가 발생한다. 결국 gradient가 모든 차원에서 0에 가까워질 때 탈출하려고 하기 때문에 매우 어려워진다.

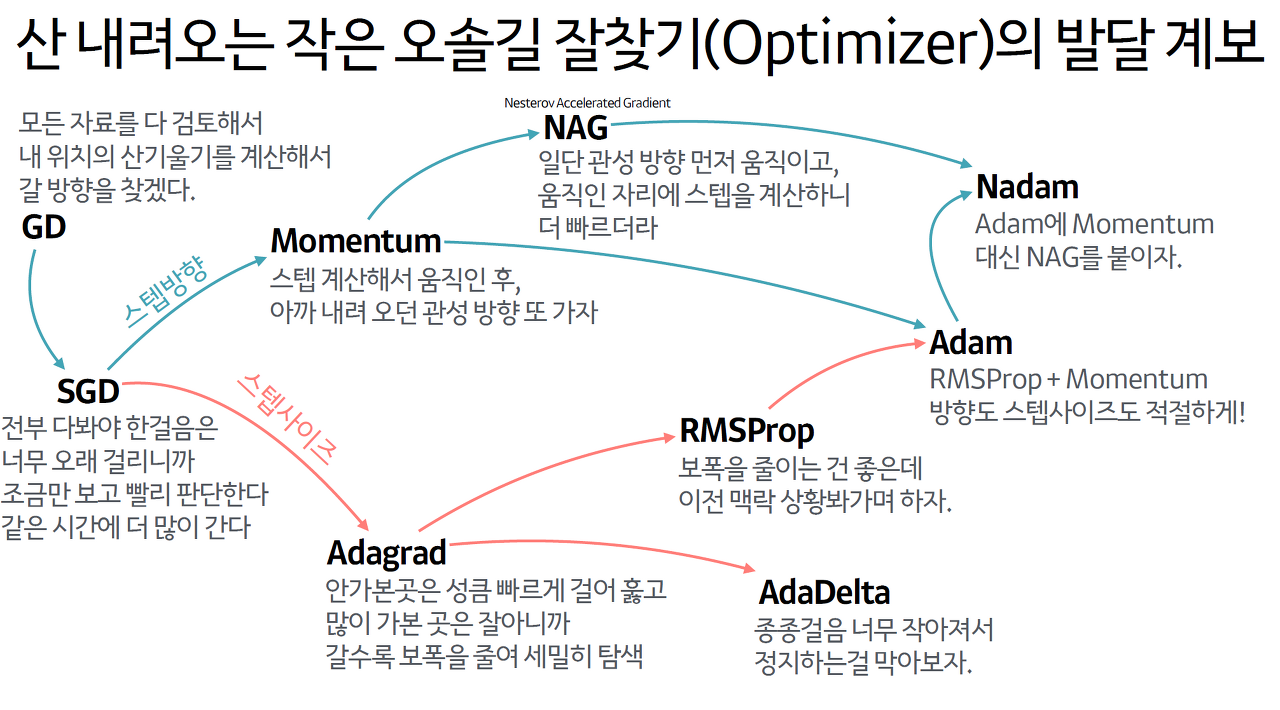
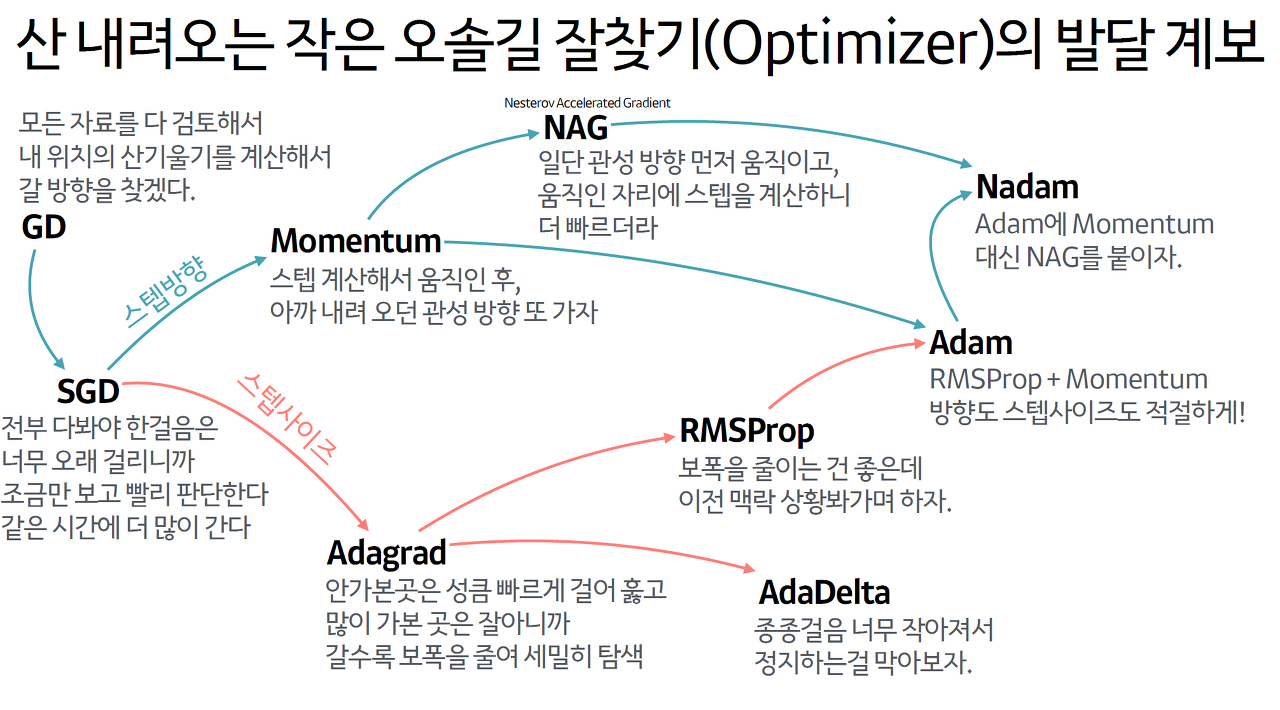
4. Gradient descent optimization algorithms

4.1 Momentum

가파른 지역에 대하여 더 가파르게 탐색하여 gradient가 같은 방향을 가르키는 차원에 대해서 더 증가하고 방향을 변경하는 차원에 대한 업데이트를 줄인다.
-> 더 빠르게 local minimum 문제를 빠져나올 수 있다.

스텝 계산해서 움직인 후에 아까 내려오던 관성 방향을 또 가겠다.

4.2 Nesterov accelerated gradient (NAG)

원래 위치에서의 gradient를 사용하는 것보단 그 방향으로 조금 더 나아가서 측정한 gradient를 사용한다.
-> 진동을 감소시키고 수렴을 빠르게 만든다.
-> 기본 모멘텀 최적화보다 훈련 속도가 빠르다.

일단 관성 방향으로 먼저 움직이고, 움직인 자리에서 스텝을 계산하니까 더 빠르다.

4.3 Adagrad

: It adapts the learning rate to the parameters, performing larger updates for infrequent and smaller updates for frequent parameters. For this reason, it is well-suited for dealing with sparse data.

빈번하지 않은 파라미터에 대해 더 큰 업데이트, 빈번한 파라미터에 더 작은 업데이트를 해준다.
매 단계에서 모든 파라미터에 대해 다른 learning rate 사용하고 분모에 제곱된 gradient가 누적된다는 특징이 있다.
하지만, 학습을 오래하게 되면 스텝사이즈가 너무 작아지게 되기 때문에 더 이상 스텝을 밟지 않는 문제가 발생한다.

안가본 곳은 더 빠르게 걸어서 훑고 많이 가본 곳을 잘아니까 갈수록 보폭을 줄여 세밀하게 탐색한다.

4.4 Adadelta

위의 Adagrad의 문제점을 해결하자.
과거 제곱 gradient를 모두 누적하는 대신 누적된 과거 gradient를 고정된 크기 w로 제한
-> 학습률을 설정한 필요가 없다.

4.5 RMSprop

보폭을 줄이는 건 좋지만 이전 맥락, 상황을 봐가면서 하자

4.6 Adam (Adaptive Moment Estimation)

RMSProp + Momentum 방향, 스텝 사이즈 모두 적절하게
각 매개변수에 대한 적응 학습률을 계산하는 또 다른 방법이다.

4.7 AdaMax

adam 논문에서 extension으로 제안된 알고리즘
learning rate를 조절하는 부분을 Lp norm으로 확장시킨 알고리즘

4.8 Nadam

Adam에 Momentum 대신 NAG를 붙이자

4.9 Visualization of algorithms

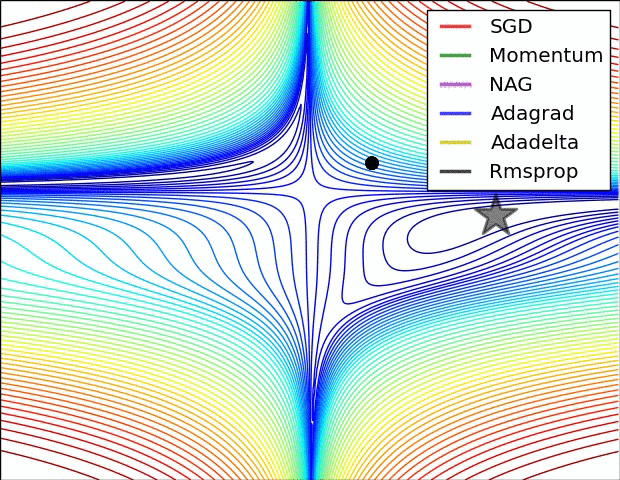
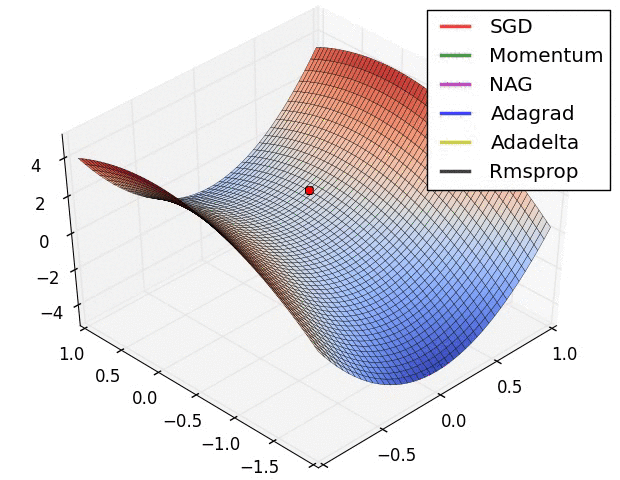
4.10 Which optimizer to use?

1. Data가 sparse 한 경우에 adaptive learning-rate method로 사용
   -> learning rate를 튜닝할 필요가 없고 성능도 좋다.
2. Adagrad의 extension인 RMSprop가 학습속도가 급격하게 작아지는 것을 방지한다.
3. RMSprop, Adaelta, Adam 비슷한 결과가 나오지만 Adam이 RMSprop보다 최적화가 끝날 때 약간 더 뛰어난 성능을 발휘하게 된다.
4. 지금까지는 Adam이 제일 !

5. Parallelizing and distributing SGD

병렬화, 분산화할 때 사용된 알고리즘 : 패스,,

6. Additional strategies for optimizing SGD

: 함께 사용할 수 있는 방법들 소개
1. Shuffling and Curriculum Learning
2. Batch normalization
3. Early Stopping
4. Gradient noise

7. Conclusion