SL Foundation

머신러닝 : Data로부터 내재된 패턴을 학습하는 과정

• Binary / Multi Class / Regression 으로 나눌 수 있음
  지도학습의 가장 큰 특징은 ‘Lable’이 존재한다는 것

구성
입력 x와 출력 y의 쌍으로 구성되어 있음
Ex) 개 이미지[x] -> h(x)-> 개[y]

• 우리는 이 h(x)를 학습시키는 것이 목표임

1. Training
   Error를 줄여나가는 방식으로 학습 진행 (Lable이 있기 때문에 가능!)
   Domain 지식을 활용한 효과적인 Feature로 학습을 진행함
    ML은 이런 Feature 도메인 지식이 필요하지만, DL은 비교적 자유로움
2. Target Function
   달성하기 어려운 위상적 함수. 데이터의 모든 대상에 대해 작업을 수행해야하기 때문
    제대로 하려면 전세계 자동차를 조사해야 하지만 현실적으로는 n개만 가능
    이런 함수를 Hypothesis 함수 => ML은 이런 Hypothesis 함수의 일종이다!!!
3. Model Selection
   : 문제에 적합한 모델을 선정하는 과정
   데이터의 특성에 따른 모델 선정이 필요

ML은 그 자체로서 데이터 결핍으로 인한 불안정성을 가지고 있다. => 일반화가 중요하다!!
관찰하지 못했던 새로운 input에 대해서도 잘 예측할 수 있는가?

• 목적 : Generalized Error를 최소화 시키는 것 by Training Error / Valid Error
  Error는 MSE, SE, BE, MAE….뭐 등등 많이 쓰던 것들 [Cost Function]

Train Error
: 주어진 sample에서 model parameter를 최적화 시키는 데에 사용
Test Error
: 전체 데이터셋에서 transet를 제외한 것. 현실 세계의 데이터를 반영한 데이터셋

Train Error를 0에 가깝게 만들거나 Train Error와 Test Error를 가깝게 만드는 방향으로 학습
Test 와 Train 을 가깝게
-실패하면 : Overfitting [high variance] // 해결법 : 규제, 데이터추가
Train을 0에 가깝게
-실패하면 : Underfitting [high bias] // 해결법 : 최적화, 모델을 더 복잡하게

Bias와 Variance는 Trade off 관계에 있음
모델의 복잡도에 따라 Overfitting / Underfitting이 발생하니 이 둘의 균형을 맞추는 것이 중요하다.

최근엔 오버피팅이 더 흔하게 일어남 [차원의 저주]

• 데이터 추가, Augmentation , Regularization, Ensemble 등이 있음
• Cross-Validation : Trainset 중 일부를 Validation set로 이용 이걸 5번 반복함 (측정용)

Linear Regression

Regression : 모델의 출력이 연속값

Linear model
Model Parameder와 x의 선형합으로 이루어질 수 있는 것 (aT * X)로 표현 가능한 것!!
(logistic regression이 비선형인 이유)
: 단순하다 (일단 해보기 쉽다) / 일반화에 좋다 / 회귀와 분류 문제 둘 다 풀이 가능
입력되는 feature들은 수치로 변환되어야 함
Regression도 지도학습이기 때문에 x – y pair로 되어 있음
단변량 문제, 다변량 문제는 변수의 수에 따라 결정됨 (단항회귀 다중회귀)

• 주어진 입력에 대해 출력과의 선형적 관계를 추론하는 것이 바로 Linear Regression 이다!!

상수항은 offset 역할

Loss Function은 MSE를 사용한다.
Parameter는 Gradient Descent를 이용해서 구함
Loss Function을 최소화 시키는 지점 [Error Surface의 최저점] 을 향해 Parameter를 조절함 -> Fitting.

Parameter Optimization
결국 target의 vector, Y 와 feature의 vector, X, parameter의 Vector P의 Error를 구하는 과정
|| Y - XP || 가 바로 loss가 됨 -> 이 loss를 최소화 시키는 parameter를 찾는 것!!
바로 직빵으로 loss =0인 parameter를 구하는 방식을 Normal Equation으로 구한다~ 라고 하는데 이런 과정은 데이터가 많아질수록 비효율적임
Why? 차원이 증가할수록 Matrix의 Inverse증가 -> 연산량이 너무 많아짐

효율적으로 구해보자!! -> Gradient Descent!!!!!

Gradient Descent 찍먹
최저점에 도달하면 기울기가 = 0 이됨 (Gradient=0)
그 지점을 찾아가는 과정임
내려가려면 기울기가 큰 방향(내리막길)로 가야함 -> Gradient가 큰 방향으로 이동! Lr을 조정함으로써 얼마나 이동할지를 결정할 수 있음
이런 걸 Greedy 알고리즘이라고 함

Global Optimum 은 전체 loss에서 가장 낮은 지점을 말하지만 local optimum은 그 지역에서만 낮은 지점을 말함

• Local엔 도달 했는데 그 지점이 global은 아닐 가능성이 항상 있음…!!
• 따라서 보폭(Learning Rate)을 Hyper Parameter로서 조절함으로써 극복 가능성을 높일 수 있음

Minimum에 도달할 때까지 내부 parameter를 update 시키는 것!!!

Normal vs Gradient
노말 : 한번에 구할 수는 있지만 데이터가 많아지면 비효율적
Gradient : 편하게 구할 수는 있지만 너무 오래걸림 -> SGD

Gradient Descent

Gradient : 벡터의 편미분값 (변화량)

Learning Rate
Lr 값의 크기에 따라 수렴 속도를 조절할 수 있음
작으면 : 안정적으로 수렴, 그러나 오래걸림
너무 크면 : 학습 진행 자체가 안 됨

• 중간정도의 lr을 선택하여 어느 정도 빠르면서 안정 적으로 수렴하는 걸 선택해야됨

Batch Gradient Descent
Local Optimum에 취약하지만 어느 정도 수렴하는 모습을 보이긴 함

• 약점 : 학습 parameter를 조절 할 때, 모든 sample에 대해 고려를 해야 한번 update가 가능함
• Data 가 커지면 커질수록 모델의 복잡도가 너무 커질 것임

SGD (Stochastic Gradient Descent)
BGD보다 빠르게 iter를 돌 수 있음!

• 약점 : 전체 sample이 아닌 특정 sample로 추론하기 때문에 noise에 취약함
• 그러나 여전히 Local Minimum에 취약함 그리고 여전히 느림

Momentum을 이용하자!!
: 업데이트 되어 오던 방향과 속도를 어느 정도 반영해서 Gradient = 0이 되더라도 학습을 계속 하게 하는 방법

• 현재의 모멘텀은 과거의 모멘텀 값과 Gradient 누적 값들을 반영함
• 현재 가치의 개념이랑 같음 !!!

Nestrov Momentum
Gradient를 먼저 보고 update!! 기존은 모멘트 스텝과 Gradient 를 벡터 합 한 것만큼 이동하지만 이건 momentum을 보기 전에 Gradient의 방향을 고려함
약간 전에는 방향과 얼마나 움직여 왔는지를 한번에 고려했다면 이건 방향 먼저 보고 생각한 다음에 얼마나 움직여왔는지를 고려한다는 말인듯.

Ada Grad
각 방향으로의 LR을 적응적으로 조절 -> 학습효율을 높임
지금까지 움직였던 방향일수록 이미 그 방향으로 학습이 많이 진행되었다는 의미 (Gradient 누적 값이 크다!)

• 그럼 LR을 슬슬 줄이자!!
• 이런 식으로 누적 Gradient를 보면서 LR을 조절하는 것
• 단점 : Gradient가 누적될수록 LR이 너무 작아지게 됨 -> 학습이 더 이상 이루어지지 않음

RMSProp
Gradient 누적 값을 계산할 때 그대로 Gradient를 곱하는 게 아니라 (1-lo)를 곱함 -> 이것도 현재가치를 계산하는 아이디어네

• 어느 정도 완충된 상태로 LR이 줄어듦

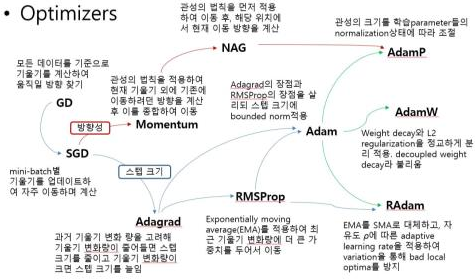
Adam (Adaptive Moment Estimation)
RMSProp와 Momentum 방식을 합침
1. 모멘텀 방식으로 첫번째 모멘텀 계산
2. RMSProp 방식으로 두번째 모멘텀 계산
3. Bias를 Correct
4. 파라미터 Update

Optimizer의 종류를 설명해주실 때, 제가 예전에 봤던 Optimizer 정리도가 생각이 나서 이 Note에 살짝 두고 갑니다!

LR Scheduler
LR을 Epoch마다 조절하는 방법
학습 초기에는 LR을 큰 값으로 진행하고 Epoch가 진행될수록 LR을 줄임!

과적합 극복 Tip
Regularization : Feature의 수를 줄이는 방법

• 학습 과정에서 모델이 복잡하더라도 이에 맞는 Penalty를 부여!
• 특정 coefficient가 안 중요하다고 판단되면 0으로 침

Linear Classification

Classification의 Label은 Discrete한 값!
Linear Model은 결국 회귀계수와 Feature가 선형 결합이 된 형태
즉, Linear Classification은 선으로 data들을 구분해내는 것이 목적이 됨
Decision Boundary로 Label을 분류해내는 것! (가정 : 데이터들이 선형구분하게 되어있다~)

• 어떤 함수를 이용할 것인가? (Decision Boundary를 형성할 함수)
• Loss Function은 뭘 쓰지? (Classification 에 좋은 손실 함수)
• Optimizer는 뭘 쓰지?

전반적인 과정은 NN과 비슷함 특정 함수에 들어가서 Boundary를 그어줄 기준을 정의해주고 거기에 맞게 Classification을 해주는 것!

Input이 함수에 들어가서 나온 output을 Score라고 하는데, 이 Score는 결국 Decision Boundary와 Data Point간의 거리가 됨(Projection 했을 때)

그럼 학습을 어떻게 시키냐?
Classification 의 Loss는 좀 다름
Zero-One : 틀리면 1, 맞으면 0을 출력
'+ Margin 사용 : Score에 y를 곱한 값이 Margin -> 정답을 잘 맞힐수록 Margin은 양수를 가지게 됨!! 틀리면 음수를 가지게 되므로 이걸로 판단

• 근데 Zero-One은 Gradient가 0이 됨

• Hinge Loss 사용
  Hinge Loss : 1-Margin값과 0 중에 큰 값을 출력함
  

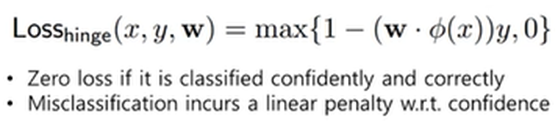
• Margin이 크면[잘 맞추면] 1-Margin은 완전 음수 -> 0이 나오게 됨 -> Loss = 0

• Margin이 작으면[못맞추면] -> 해당 값이 나옴 -> Loss 그대로 출력
  

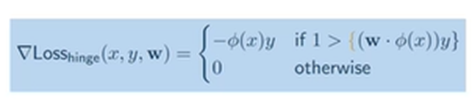
• 따라서 이렇게 Gradient가 나오게 됨

Cross-Entropy Loss
KL발산에 기반함! 다르면 다를수록 loss가 커지고 같으면 같을수록 작아지는 형태

• 확률 값을 서로 비교하게 됨 -> Score를 어떻게 확률로 나타낼까?
• 0-1 사이로 나타내기에 가장 좋은 거 = Sigmoid!!!
• 어떤 값이 들어오든 0 ~ 1 사이의 값을 가지게 해줌
• Logistic Model
  실질적으로는 각 Lable에 대해 확률 Vector가 들어옴 그리고 Lable Vector도 Label Encoding 형태로 존재!! 이 둘의 차이로 Loss 계산하면 된다!!

Training 과정
1. 가중치 초기화
2. Gradient 계산
3. 이동 방향, 정도 계산
4. 가중치 Update
5. 수렴할 때까지 반복

Multiclass Classification
Ex) One vs All : A냐 아니냐 B냐 아니냐 -> Multi를 Binary로 풀어냄! -> 이걸 Class별로 반복해서 Score를 얻고 확률값으로 나타냄 -> Cross Entropy loss 계산하고 업데이트!

Linear Classification의 장점
간단하다 / 해석하기 쉽다

Advanced Classification

아까처럼 Decision Boundary를 그을 건데, 그릴 수 있는 것중에 뭘 고르지? 최적의 분류 선은 어떻게 고를 수 있을까? -> 새로운 Data가 들어와도 강건한 선을 그어야 함

SVM (Support Vector Machine)
Margin을 기준으로 결정하자!!!

• 각 Class에서 Decision Boundary와 가장 가까운 Data Point들 간의 거리의 중간!
• 즉 각 Data Point에서 가장 큰 Margin을 가지게 하는 Line을 긋는 것!
• 가장 가까운 데이터 포인트가 Surpport Vector! Robust한 특징이 있음
  최적화 방법

Hard Margin SVM : SV들과 Boundary 사이엔 그 어떤 데이터도 없어야 한다.
Soft Margin SVM : 몇 개는 있어도 돼~

Hard Margin SVM

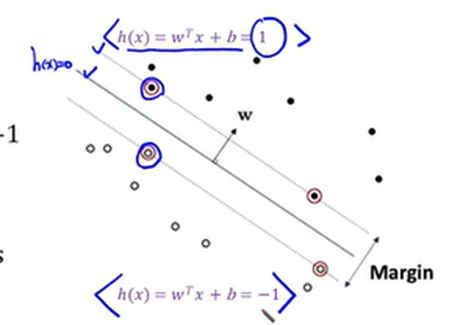
이렇게 나타낼 수 있음 (Scaling을 통해 -1과 1 사이의 값을 가지게 만듦)
때문에 Boundary의 거리를 2/||w||로 나타낼 수 있고, 이게 바로 Margin임
그리고 이 식을 최대화 시키는 것이 목적! 즉, ||w||를 최소화 시켜야함 -> 계산이 귀찮아지므로 ||w||^2를 최소화 시키는 것을 목표로 함

• 어… 근데 데이터들이 선형으로 구분할 수 없게 생겼으면 어떡하지?
• Kernel 사용

Kernel 함수
Polinomial / RBF / Hyperbolic Tangent 등을 활용해서 비선형적으로 분포된 애들도 선을 그을 수 있음

ANN (Artificial Neural Network)
앞서 했던 내용과 굉장히 비슷함 이름만 바뀌었을 뿐

Activation Function
Sigmoid : 층을 깊게 하면 별로 안 좋게 됨… Gradient가 어차피 갈수록 작아지게 됨
ReLU : 미분해도 0 아니면 1의 값을 가짐

• 근데 이것도 Gradient 폭발 문제가 있어서 Leaky ReLU!

핵심은 비선형적인 층을 쌓으면 아무리 복잡한 형태라도 표현할 수가 있다는 것!!

• NN이 기본이 되는 이유임!

XOR문제도 해결 가능 (제 블로그 가시면… 쉽게 설명했습니다 ㅎㅎ)
이런식으로 여러 층을 쌓은 모델을 MLP라고 함!!!
이런 여러 층의 모델들은 이미지, Video와 같은 고차원의 이미지에 적합함!!

물론 너무 계속 쌓아가다 보면 오히려 성능이 낮아지는 경우가 있음 (By Gradient Vanishing)

• 미분 값이 계속 작아지면서 깊은 층에대해 서는 학습이 잘 진행되지 않는다.
  오차역전법은 살짝 그냥 넘어가심

Ensemble

알고리즘 종류에 상관없이, 여러 모델들을 묶어 함께 사용하는 방식
Ex ) SVM + NN

여러 학습 데이터들을 같은 데이터에 대해 결과들을 투표해서 최종 결과를 결정함

• 하나의 모델의 결정이 아니라 여러 모델의 결정!

장점 : 노이즈에 강건함, 구현하기 쉬움, 파라미터 튜닝이 많이 필요 없음
단점 : 모델 자체로 Compact한 표현하기가 어려움

Bagging
학습 데이터를 n개로 구분하여 n개의 Classification에 각각 학습시킴 -> 각각 다른 특성을 학습할 수 있다!!

• 병렬적으로 학습 가능!!!
• Augmentation 효과 기대 가능

Bootstrap
Sample Data Set을 생성해서 학습하는 방식
어차피 다른 모델로 학습 시킬 거면 같은 Data로 학습 시켜도 큰 상관 없음

• 오히려 Noise에 강건하게 됨
• 모델이 n개면 data를 n개 복붙해서 학습!

Boosting
Weak Classifier들을 여러 개로 묶어서 이전 Classifier가 데이터를 학습할 때의 정보를 반영함!!
Weak Classifier : Bias가 높은 Classifier (단순해서 혼자서는 성능 x)

• 그러나 이들을 Cascading하면 높은 성능을 기대할 수 있다!!!!
  
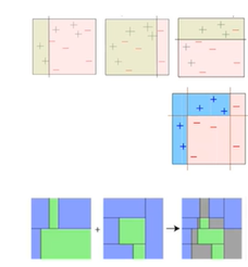
  이런 식으로 복잡한 문제도 해결할 수 있다

Ada Boost
연속적인 Classfier들로 분류작업이 진행 될 때마다 데이터에 가중치를 둬서 성능을 향상

평가
Accuracy : 가장 흔하게 사용
Confusion Matrix

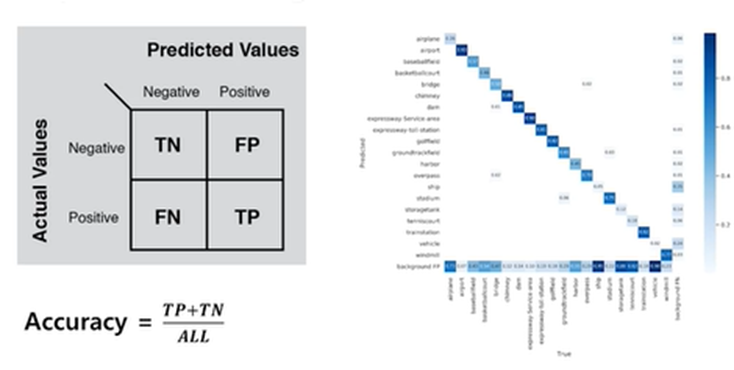
이런 식으로 표현 가능하다는 말
FP : N인데 P라고 판단함 (틀린 Positive)
TP : 잘 맞춘 P
Precision : TP/(TP+FP) | Recall : TP/(TP+FN)

• 불균형 데이터인 경우 Precision과 Recall도 동시에 고려해야 제대로 측정 가능하다

풀고자 하는 문제에 따라 적합한 Metic을 사용해야함

Object Detection / Image - Sentence / Segmentation 도 SL로 풀어냄
SL이 진짜 좋긴 한데 데이터가 많이 필요한 것이 한계임

• Data Augmentation 필요 / Label이 꼭 필요함
• 도메인이 바뀌었을 때 어떻게 적응 해야하는가? 도 이슈!!