Casuality

인과성 : 하나의 어떤 무엇인가가 다른 무엇을 생성함에 있어서 영향을 미치는 것

• 부분적인 관계 -> 꼭 필요조건이나 충분조건일 필요는 없다.

법칙 : 원인과 결과의 관계를 기술한 것!

인과성과 데이터 사이언스의 연관성
AI가 특정 목적을 이루어 내도록 학습시키는 것

• 강화학습 : 환경에 변화를 줘서 원하는 상태로 변화시키는 것이 목적
• 기계학습 : 데이터의 상관성 학습이 목적
• 데이터 사이언스 : 수집하고 분석한 데이터로 대중들과의 소통 – 상관성과 인과성

Pearl의 인과 계층
1.관측 계층 (Associational or Observational)
시스템을 건들지 않고 그대로 관찰하면서 변수들의 상관성 관찰

2.실험 계층 (Interventional or Experimental)
실험을 함으로써 나오는 결과에 관심 (A/B 테스트)

3.반사실적 계층 (Counterfactual)
실험 통제를 통해 나온 결과가 아닌 실험 통제를 하지 않았으면 결과가 어땠을지를 생각하는 것

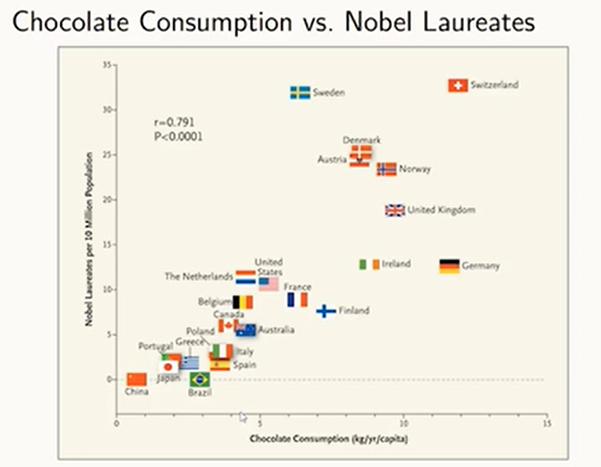
이런 그림이 있을 때 우리는 어떻게 해석해야 할까?
일단 1단계 계층으로 해석 가능
부유한 나라 : 기초과학에 많이 투자 + 초콜릿 같은 디저트도 많이 섭취 가능

심슨의 역설 : 기존에는 조건부(결석의 크기)로 처방을 결정했지만, 전체 집단에 적용할 때는 그런 조건부 없이 실험을 하기 때문에 결과는 다를 수 있음. 즉, 실험 집단의 인과적 관계에 대한 자세한 이해가 필요하다!

데이터를 볼 때 먼저 생각해야 하는 것
1. 주어진 데이터가 상관성을 가지고 있는지 인과성을 가지고 있는지
2. 우리가 알고자 하는 것이 상관성인지 인과성인지

그럼 계층을 넘나드는 추론은 어떻게 할 수 있을까?
Black Box로부터 관찰 결과들이 나오고 이를 통해 실험 데이터를 얻을 수 있기 때문에 블랙박스에 대한 수학적 이해가 필요하다.

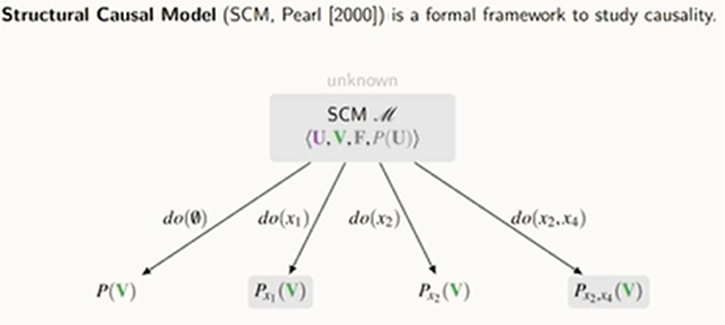
do() 안에 실험을 뭘 했는지를 적고, 그 결과를 P(V)로 함
Causal Diagram을 보고 아 이건 어떨 거야~ 라고 대충 예측할 수 있다.

Intervention(실험)
Y에 미치는 X의 영향력을 보기 위해 X에 다른 영향을 주는 Z에 대한 영향력을 삭제하고 X가 Y에 주는 X만의 영향력을 봄

• 인과 효과 : 임의의 변수 집합 X가 고정되었을 때, Y가 특정 값을 가질 확률?

때문에 그래프를 통해 인과관계를 추론해내야 하는데 그때 제일 많이 나타나는 게 조건부 독립성

이런 식으로 그래프를 통해 조건부적인 관계를 봄으로써 인과추론을 해내는 것
(중간에 다른 변수를 껴야하냐 안 껴야하냐 이런 걸로 확인 가능)

d-separation이 위와 같은 것을 컴퓨터 적으로 해석해낸 것

Causal Effect Identification

인과 효과를 계산해내는 방법
Identification : 특정할 수 있느냐?
Y에 영향을 주는 변수가 W X Z 가 있다고 하고 Z는 X에 영향을 준다고 할 때,
Z가 X에 주는 영향력을 제거한 뒤에 다시 X가 Y에 주는 영향력을 구함
즉, 인과관계를 계산하는 건 결합확률 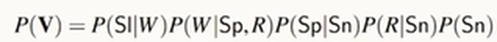에서 보고자 하는 변수를 적절히 통제해서 계산하는 것!

• 그러나 이런 방법은 그래프에 나타나는 모든 변수들이 관측 가능함
• 그렇지 않다면 어떻게 계산해야 하지?
  

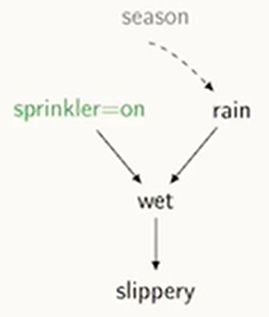
즉, 다시 말해 이 상태라면?! Season이라는 변수를 모를 때

• 스프링 쿨러를 중재했을 때 이때는 Rain을 가지고 보게 됨
• 이런 걸 Adjustment Formular 라고 함

Back - door
아까처럼 종속변수 Y, 독립변수 X, Z가 있고 Z는 X에 대한 교란 변수일 때
X의 Y에 대한 영향력을 보려면 Z에 대한 교란성을 제거해야함

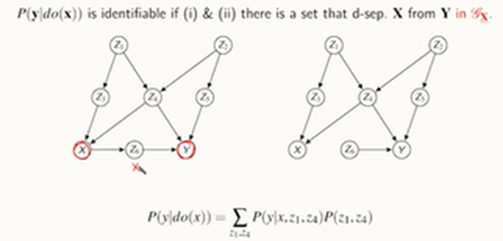
이런 식으로 복잡한 관계도 있을 수 있음. 이들을 모두 고려해서 Back door를 막기 위해선 Z4와 Z1 모두 막아야함

그러나 Back- door는 특수한 상황에서만 적용 가능 -> 몇몇 Formular는 찾을 수 있지만 모든 Formular는 찾을 수 없다

Do - Calculus
여러가지 다른 중재 조건에서 나오는 확률들끼리 서로 연결고리를 만들어주고 서로 다른 중재로 어떤 확률 분포를 바꿔주는 역할
1.Rule 1 : Adding / Removing Observations

• 관찰에 대한 것이 추가되거나 삭제될 수 있다. : 조건부 독립
• 조건부 독립은 중재된 상황에서도 넣을 수 있다.

2.Rule 2 : Action / Observation Exchange

• Action과 Observation을 바꿀 수 있다.

3.Rule 3 : Adding / Removing Actions

• Action이 추가되거나 제거될 수 있다.
• 확률을 추론하는 데에 있어서 Action은 영향을 주지 않는다.
  즉, 어떤 규칙에 의해 조건부 독립을 만족하면 확률을 다른 확률로 변경시킬 수 있다!!

Do-Calculus는 Sound하고 Complete하다.

• 인과효과를 이끌어낼 수 있는지 없는지를 빠르게 계산 가능하다!

Modern Identification

지금까진 주어져 있는 도메인을 다뤘음

• 여러 종류의 데이터를 한번에 활용하면 좋지 않을까?

Ex) 다양한 도시에서 온 다양한 변수에 대한 Data

• Sampling 방법도 다 다를 수 있음.
• 이렇게 발생하는 편향과 같은 요소를 다 고려해서 어떻게 계산을 해야할까?

Ex2) 각각의 약에 대해 실험한 데이터가 있을 때, 두 약을 혼용했을 때의 효과는?

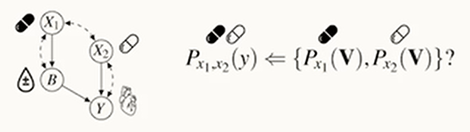
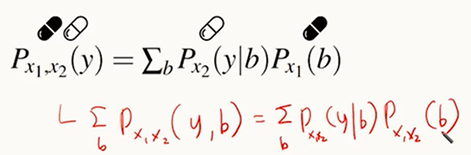
이런 식으로 계산 가능!

ML에서는 Training과 Test가 같은 환경에서 나온 것을 가정함 => 같은 도메인을 가정한다는 말과 같음!!

Transportability : 데이터 소스와 추론하고자 하는 타겟의 도메인이 다를 때의 인과 추론

• 미국의 교육 실험은 한국에서 그대로 적용 가능할까?
• Generalization으로 통계학에서 많은 연구가 이루어짐
• 즉, 단순 인과추론이 아니라 통계적 추론이라고 할 수 있음

1. Source와 Target이 같다면 그대로 적용 가능

2. 다르다면 not transportable

3. 부분적으로 같다면 ? -> Transportability의 목적
   -Source와 Target의 일부 정보들을 결합함으로써 추론 가능

4. 교란변수 Z의 Child에 차이가 있는 경우
   -상관 없이 Source로 Target 추론 가능

5. Mediator Z에 차이가 있는 경우
   

   이렇게 가능
   

보통 무작위 실험을 통해 얻는 결과를 절대적으로 받아들이는 경우가 많음 -> 실험집단과 추론집단의 차이를 고려하고 적용해야한다!! (Transportability 적용!)

Sampling 과정에서 Bias가 발생한 경우

• Selection Bias
  
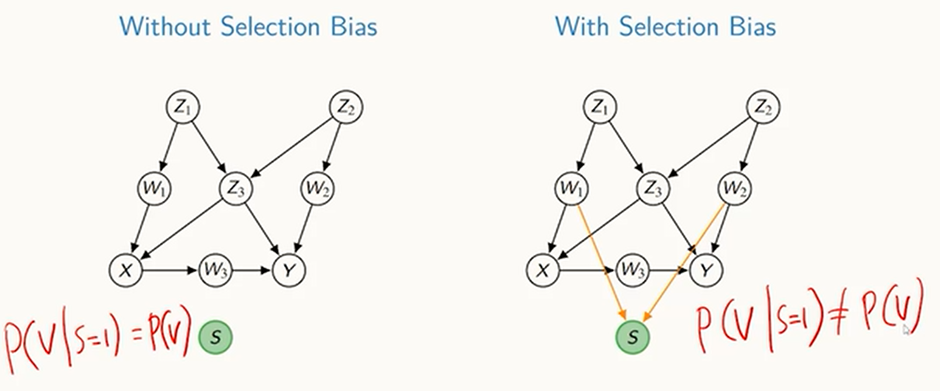
  이렇게 왼쪽은 무작위인 상황과 같은데, 오른쪽은 무작위인 상황이라고 할 수가 없게 됨
  여러 가정들을 적용함으로써 인과 효과가 편향없이 계산될 수 있는지 확인해보고 계산해야함

Missing Data
데이터가 누락 됐을 경우 Diagram에 어떻게 넣을 것인가?

• 실제 학생의 비만도를 넣는 것
• 비만도가 누락되는 메커니즘 확인
• 완전 무작위
• 누락된 변수와 메커니즘 사이에 어떤 조건부 독립이 성립
• 랜덤하지 않은 누락